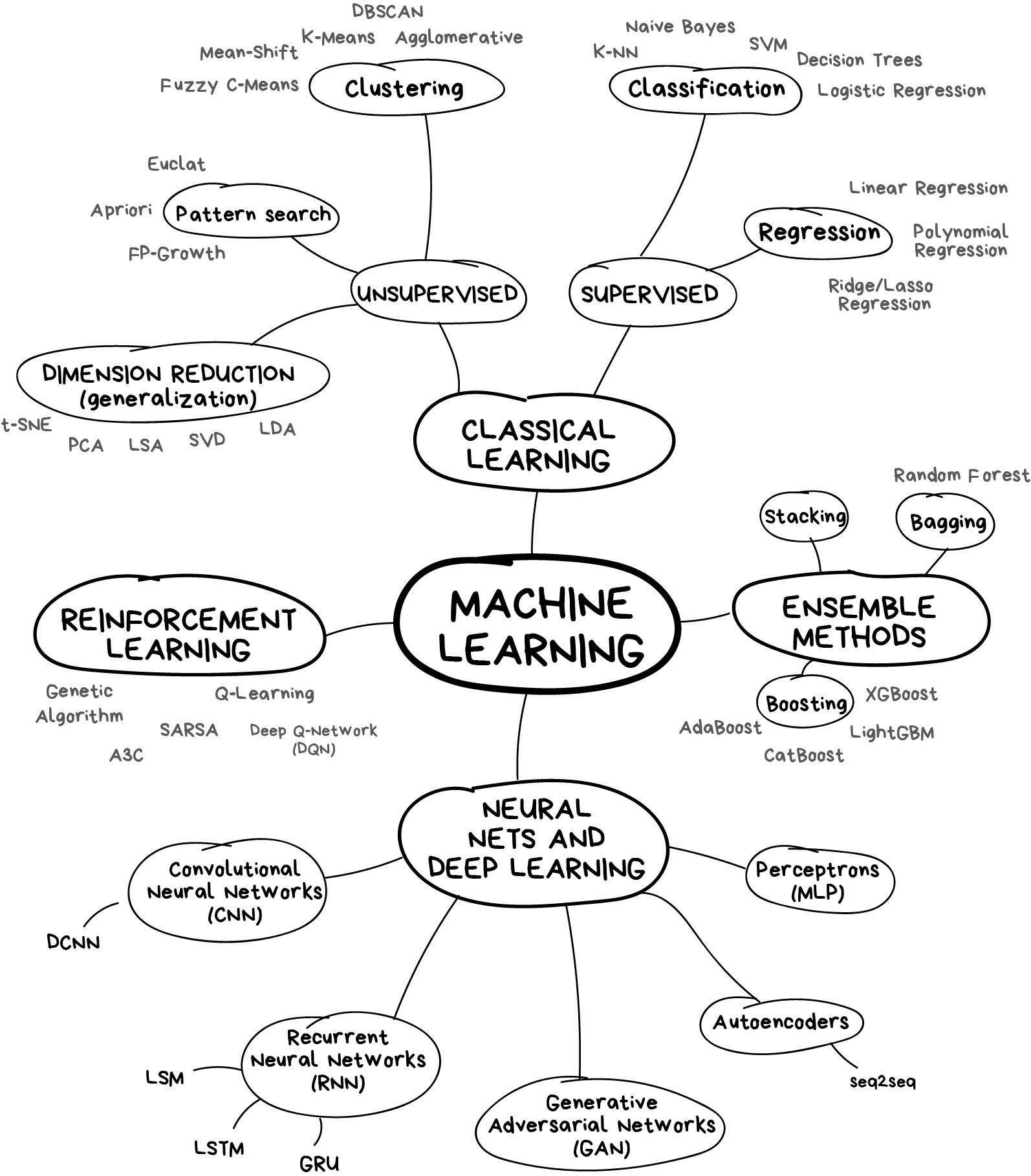
5 Intro. aprendizaje automático
Introducción inicial al aprendizaje automático
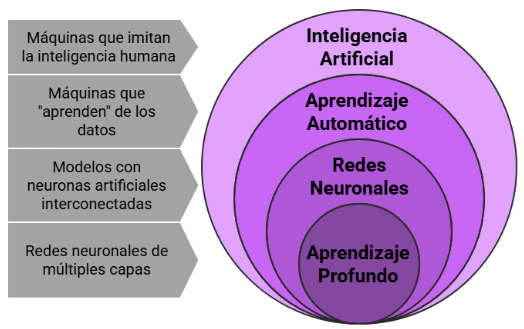
¿La inteligencia artificial consistirá en el diseño de sistemas capaces de ejecutar de manera autónoma tareas que suelen considerarse “inteligentes”?
¿Un agente inteligente se podría considerar como un sistema que percibe su entorno y toma decisiones encaminadas a maximizar sus posibilidades de éxito?
¿El aprendizaje automático se podría entender como la capacidad de ciertos programas para mejorar su desempeño sin intervención directa?
¿Será que el aprendizaje automático consiste en que de alguna manera los programas “aprendan” a partir de los datos de situaciones observadas, y generalicen ese conocimiento de manera adecuada a datos de situaciones nuevas?
5.1 ¿Aprendizaje automático (machine learning)?

El 24 de febrero de 1956 se presentó en televisión el programa de damas creado por Arthur Samuel para el computador IBM 701. Años más tarde, en 1962, el autoproclamado maestro de damas Robert Nealey se enfrentó a una versión del juego en un IBM 7094, y fue derrotado por la máquina. Aunque el programa de Samuel perdió en otras partidas, este logro se considera un hito en el desarrollo de la inteligencia artificial y ofreció al público de comienzos de los años sesenta una muestra del potencial de las computadoras electrónicas.
<www.ibm.com>
“Machine learning refers to the use of formal structures (machines) to do inference (learning).”
Clarke, B., Fokoue, E. & Zhang, H.H., (2009). Principles and theory for data mining and machine learning.
“…Vast amounts of data are being generated in many fields, and the statistician’s job is to make sense of it all: to extract important patterns and trends, and understand ‘what the data says’. We call this learning from data.”
Friedman, J., Hastie, T. & Tibshirani, R., (2009). The elements of statistical learning.
Recordemos que usando programación “clásica” o “tradicional” (imperativa estructurada procedimental):
Al computador le damos explícitamente un algoritmo asociado a lo que hace una función dada f, de modo que, cuando le demos un valor de entrada x, este nos dé el valor de salida y tal que y = f(x).
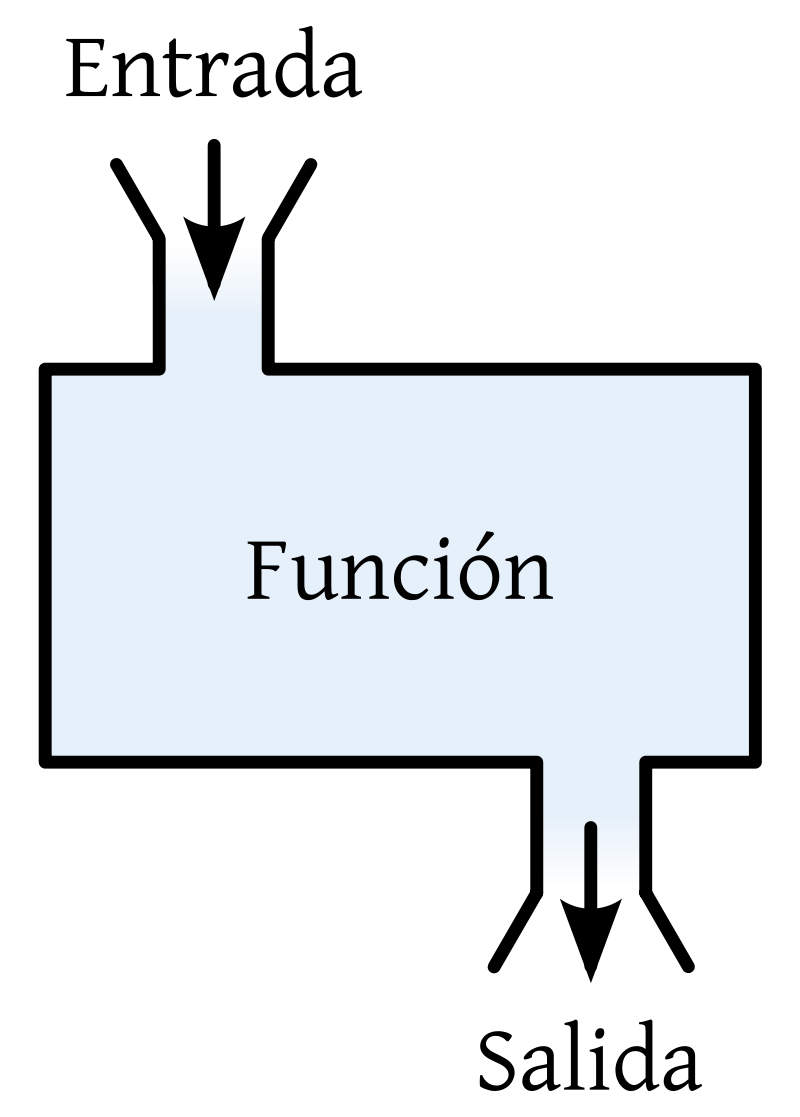

Con esta clase de “programación”, ¿cómo programaríamos a un computador para que eventualmente gane a las damas o al ajedrez, reconozca dígitos escritos a mano, o en general, para que prediga salidas o respuestas y para valores de entrada x, en donde no sabemos cuál es la función / algoritmo / “máquina” que debería usarse?
5.1.1 ¿Aprendizaje supervisado?

Al computador le damos la mayor cantidad de x_i (features) y y_i (target), \left(x_i, y_i\right) que podamos, para que de alguna manera nos dé la mejor “máquina” f que pueda, tal que y_i \approxeq f(x_i) o y_i - f(x_i) \approxeq 0 para todo i.
Pero también queremos que a su vez se le pueda dar un valor no dado antes x_0, para quien no tenemos y_0, y que el computador nos “prediga” cuál debería ser el valor de ese y_0.
En este caso, la “predicción” suele ser el objetivo principal.
Se busca resolver problemas de regresión (las y_i son valores de una variable cuantitativa) o de clasificación (las y_i son valores de una variable cualitativa).
Todos los modelos del modelado estadístico que se puedan usar para “predecir” y’s se pueden considerar máquinas de aprendizaje supervisado.
5.1.1.1 ¿Problema de regresión?
Encontrar la “máquina” f que generaliza la relación entre Y (cuantitativa) y X_1, X_2, \dots:
5.1.1.2 ¿Problema de clasificación?
Encontrar la “máquina” f que generaliza la relación entre Y (cualitativa) y X_1, X_2, \dots:
Y = f(X_1, X_2, X_3, \dots)

| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| … | … | … | … | … |
5.1.2 ¿Aprendizaje no supervisado?

Al computador le damos la mayor cantidad de x_i que podamos, para que de alguna manera nos dé el mejor f y los mejores y_i’s que pueda, tal que y_i \approxeq f(x_i) o y_i - f(x_i) \approxeq 0 para todo i.
En este caso, el objetivo es explorar los datos (Exploratory Data Analysis) para identificar patrones (Pattern Recognition), extraer conocimiento (Knowledge Discovery) o realizar lo que en ocasiones se ha denominado minería de datos (Data Mining).
Es decir, se desea producir y’s que capturen, representen o reflejen algo que no fue explícitamente observado, por ejemplo, la asociación entre variables o la asociación entre individuos.
Las técnicas de estadística descriptiva multivariada para la reducción de la dimensión y para el agrupamiento (clustering) harían parte del aprendizaje no supervisado.
5.1.2.1 ¿Problema de reducción de la dimensión (asociación entre variables)?
Encontrar una Y a partir de los valores que toman X_1, X_2, X_3, \dots, con la respectiva f, que sintetice la asociación entre las variables, y que dé la posibilidad de ser efectivo y eficiente, con la información “redundante” que podría afectar negativamente nuestro trabajo.
5.1.2.2 ¿Problema de agrupamiento (asociación entre individuos)?
Asignar un grupo a cada individuo / instancia bajo algún criterio, es decir encontrar una Y categórica a partir de los valores que toman X_1, X_2, X_3, \dots (con la respectiva f que las relaciona):
5.2 ¿Máquina de aprendizaje?
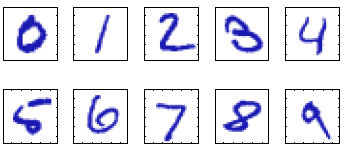
Consideremos el ejemplo de reconocimiento de dígitos escritos a mano.

Cada dígito corresponde a una imagen en escala de un solo color (por ejemplo, escala de grises) y de 28 \times 28 pixeles. Esta puede representarse mediante un arreglo x que contiene 784 números entre 0 y 255 (o entre 0 y 1).
El objetivo es obtener una función f que tome un vector x como entrada y que produzca la identidad del dígito como salida, es decir un número de estos: (0, \dots, 9).
Para definir una máquina de aprendizaje es necesario tener en cuenta que desde el comienzo tenemos un espacio de entrada, digamos \mathcal{X}, en el cual están los objetos a los cuales se les desea hacer una asignación de un objeto que está en otro espacio de salida, que vamos a denotar \mathcal{Y}.
La definición de los dos espacios depende del problema.
Una máquina de aprendizaje es una función f que asocia a cada elemento de \mathcal{X} un único elemento en \mathcal{Y}.
Escribiremos
f : \mathcal{X} \to \mathcal{Y}
Si x es un elemento del espacio \mathcal{X}, escribimos x\in\mathcal{X}, entonces la notación y = f(x), significa que y es el único elemento de \mathcal{Y} asociado a x.
En este ejemplo, el espacio de entrada \mathcal{X} es el conjunto de todos los arreglos de tamaño 28 \times 28, cuyos valores están en el intervalo [0,255]. Este espacio es finito, pero muy grande: 256^{784} posibles imágenes.
Adicionalmente, el conjunto de salida \mathcal{Y} es el conjunto de etiquetas \{0,1,2,3,4,5,6,7,8,9\}.
5.2.1 ¿Entrenamiento de una máquina de aprendizaje?
La construcción de una máquina de aprendizaje requiere encontrar valores para un conjunto de parámetros que definan de manera específica a la función f, es decir, encontrar \hat{\theta} \in \Theta tal que f \approxeq f_{\hat{\theta}} \in \left\{ f_\theta: \theta \in \Theta \right\}
El proceso de encontrar tales parámetros se conoce como entrenamiento o aprendizaje de la máquina.
Es decir el entrenamiento consiste en encontrar (estimar) valores para tal conjunto de parámetros.
El entrenamiento de una máquina de aprendizaje es una forma de modelado.
Básicamente el proceso de entrenamiento utiliza un conjunto de datos del espacio de entrada y las etiquetas o valores asociados en el conjunto de salida.
5.2.2 ¿Conjunto de entrenamiento?
Al adoptar un enfoque de aprendizaje de máquinas, el conjunto de dígitos (datos) utilizado para entrenar la máquina de aprendizaje es llamado un conjunto de entrenamiento.
5.2.3 ¿Valores o etiquetas objetivo (target)?
Las categorías (etiquetas) de los dígitos en el conjunto de entrenamiento se conocen de antemano, generalmente ya se revisaron y se etiquetaron manualmente.
Podemos expresar la etiqueta de un dígito usando un arreglo objetivo que representa la identidad del dígito correspondiente.
5.2.4 ¿Codificación one-hot?
En el párrafo anterior parece extraño mencionar que en la salida hay un arreglo.
En realidad, cuando se tienen varias etiquetas no numéricas, es conveniente recodificar las etiquetas usando arreglos binarios.
Esto se hace de la siguiente manera:
- Si se tiene p etiquetas, digamos 10 en el caso de los dígitos, entonces las etiquetas se convierten en arreglos unidimensionales de tamaño p, en donde todos los elementos son cero excepto en la posición que corresponde a la etiqueta que representa.
La siguiente tabla ilustra la codificación one-hot en el caso de los dígitos.
| dígito | one-hot |
|---|---|
| 0 | 1000000000 |
| 1 | 0100000000 |
| 2 | 0010000000 |
| 3 | 0001000000 |
| 4 | 0000100000 |
| 5 | 0000010000 |
| 6 | 0000001000 |
| 7 | 0000000100 |
| 8 | 0000000010 |
| 9 | 0000000001 |
La codificación one-hot es utilizada cuando se tienen variables categóricas.
Esta es una forma en la cual datos categóricos y datos numéricos pueden interactuar.
Por ejemplo, si una variable en el espacio de entrada es color, y hay digamos 3 colores: rojo, verde y azul, entonces la codificación one-hot puede ser:
| color | one-hot |
|---|---|
| rojo | 100 |
| verde | 010 |
| azul | 001 |
En este caso, la variable de entrada color es reemplazada por las tres columnas de la codificación one-hot.
5.2.5 ¿Algoritmo de entrenamiento?
Los algoritmos de entrenamiento de las máquinas de aprendizaje consisten básicamente en procesos de optimización de una función objetivo, que denominaremos función de pérdida.
Por ejemplo, supongamos que los valores objetivo \{y_1,\ldots,y_n\} de la máquina de aprendizaje son números reales y que los datos de entrenamiento son digamos \{x_1,\ldots, x_n\}:
- En cada paso del proceso de entrenamiento, la función candidata calculada en x_i entrega un valor digamos \tilde{y}_i.
- Este valor en principio es diferente de y_i, debido a que justamente estamos entrenando la máquina para que “aprenda” que y_i=f(x_i).
- Entonces una función de pérdida se puede definir como sigue,
\mathcal{Loss} = \tfrac{1}{n}\sum_{i=1}^{n}(y_i - \tilde{y}_i)^2.
El propósito del algoritmo de entrenamiento es encontrar valores para \theta de un función f_{\theta}, que haga que la función \mathcal{Loss} alcance un mínimo.
Sin embargo, un algoritmo de aprendizaje puede que no sea capaz de encontrar valores para el conjunto de parámetros que minimicen globalmente a la función de pérdida.
5.2.6 ¿Capacidad de generalización?
La capacidad de un máquina de aprendizaje para etiquetar correctamente nuevos ejemplos (no vistos antes por la máquina) se conoce como capacidad de generalización.
Buscamos máquinas con muy buena capacidad de generalización.
5.2.7 ¿Conjunto de testing (¿prueba?)?
La capacidad de generalización de una maquina de aprendizaje se evalúa con un conjunto de datos de entrada con sus respectivas etiquetas, que tengan la misma estructura de los datos de entrenamiento.
Por ejemplo, si en el conjunto de datos de entrenamiento usamos 70,000 datos, es decir, 70,000 imágenes con sus respectivas etiquetas, entonces podríamos seleccionar 60,000 para entrenar a la máquina y en consecuencia 10,000 para el testing.
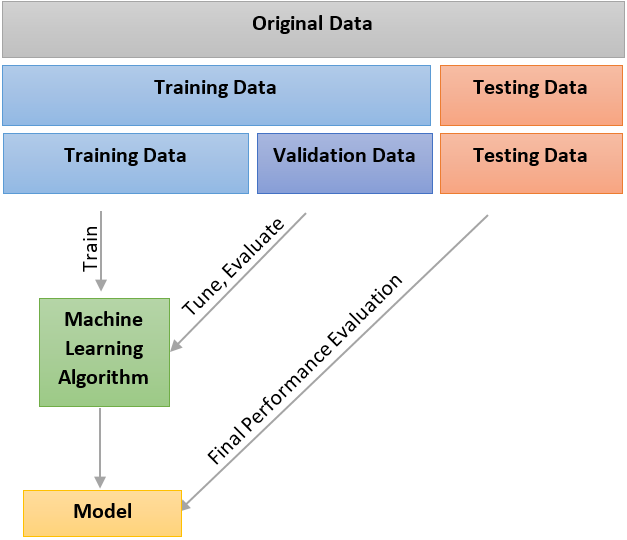
La división de los datos en conjuntos de entrenamiento y prueba es una etapa crítica en cualquier proceso de aprendizaje automático, ya que de ello depende la capacidad del modelo para generalizar correctamente a datos nuevos.
No existe una única proporción ideal, sino recomendaciones que varían según el tamaño del conjunto de datos, la naturaleza del problema y la complejidad del modelo que se va a entrenar.
-
Regla clásica: 70/30 o 80/20
En la mayoría de los casos se reserva entre el 70 % y el 80 % de los datos para el entrenamiento del modelo, y el restante 30 % o 20 % para la prueba.
Esta proporción es adecuada cuando se dispone de un conjunto de datos de tamaño medio, por ejemplo, de varios miles o decenas de miles de observaciones.
El objetivo es que el modelo tenga suficiente información para aprender los patrones generales, pero también contar con un subconjunto de prueba lo bastante grande para evaluar su desempeño de forma representativa.
-
Conjuntos de datos pequeños
Cuando la cantidad de datos es limitada, realizar una simple división puede desperdiciar información valiosa. En estos casos se recomienda emplear validación cruzada (k-fold cross-validation).
Este método consiste en dividir el conjunto completo en k subconjuntos (comúnmente k = 5 o k = 10), entrenar el modelo k veces usando k-1 subconjuntos para entrenamiento y el restante para prueba, y finalmente promediar los resultados.
De esta manera, cada observación se usa tanto para entrenar como para evaluar, y se obtiene una medida más estable del rendimiento del modelo.
-
Conjuntos de datos grandes
Cuando el volumen de datos es muy alto, no es necesario destinar una gran fracción al conjunto de prueba.
Es suficiente con que el conjunto de prueba sea representativo de la distribución de los datos.
En tales casos se puede usar una división de 90 % entrenamiento / 10 % prueba o incluso 95 % / 5 %, ya que con millones de registros, incluso el 5 % representa una cantidad considerable para evaluar el modelo con fiabilidad.
-
Cuando también se utiliza un conjunto de validación
En modelos más complejos, especialmente en aprendizaje profundo o en tareas donde es necesario ajustar hiperparámetros, se introduce un tercer subconjunto denominado validación.
Este conjunto se utiliza exclusivamente para el ajuste del modelo sin que los datos de prueba intervengan en el proceso.
Una repartición típica en este caso es 60 % entrenamiento / 20 % validación / 20 % prueba, aunque también puede ser 70 % / 15 % / 15 % si el tamaño total lo permite.
Con esta estructura, el conjunto de prueba se reserva estrictamente para la evaluación final, garantizando que no haya contaminación entre etapas.
-
Buenas prácticas adicionales
Si el problema es de clasificación con clases desbalanceadas, las divisiones deben ser estratificadas, lo que significa mantener en cada subconjunto la misma proporción de clases que en el conjunto total. Esto evita sesgos en el entrenamiento y en la evaluación.
Debe evitarse cualquier fuga de información: los datos de prueba no pueden influir en el proceso de entrenamiento, ni directa ni indirectamente, ya que esto invalidaría la evaluación del modelo.
En el caso de series de tiempo, no se deben mezclar observaciones pasadas y futuras. Siempre se entrena con los datos anteriores en el tiempo y se evalúa con los posteriores, de manera que la validación respete el orden cronológico natural del fenómeno.
En síntesis, la decisión sobre cómo dividir los datos depende de un equilibrio entre la cantidad de información disponible para el aprendizaje, la necesidad de una evaluación robusta y la prevención de sesgos o fugas de información.
5.2.8 ¿Extracción de características?
Para la mayoría de las aplicaciones prácticas, las variables de entrada originales generalmente se preprocesan transformandolas en un nuevo espacio de variables donde, se espera, que el reconocimiento de patrones sea más fácil de resolver (donde el algoritmo de entrenamiento funcione mejor).
Esta etapa de preprocesamiento es a veces también llamado extracción de características (feature extraction).