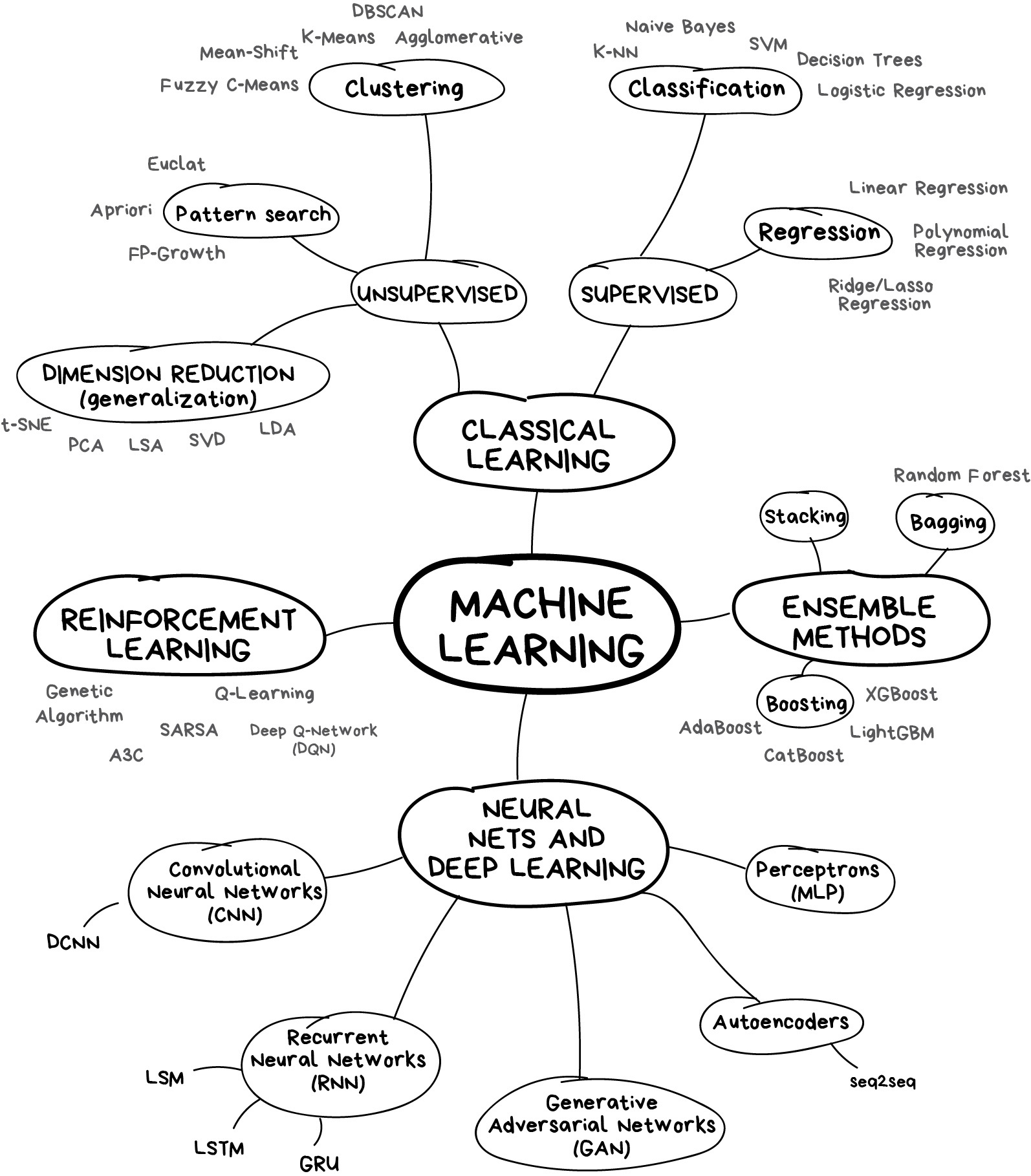
Aprendizaje automático
Modelar
Nuestro objetivo principal dentro del modelado es la “descripción” y/o la “predicción”. Partimos de unas hipótesis que nos permiten de alguna manera ver el problema de manera más sencilla y así obtener conclusiones válidas del tema estudiado. Advertencia: Es muy importante tener muy claras las hipótesis sobre las que se está trabajando, ya que una hipótesis errónea puede llevar a falsas conclusiones.
Supongamos que una empresa produce lámparas LED y que el tiempo de vida útil de estas lámparas (variable Y) está relacionado con la cantidad de electricidad que pasa a través de ellas durante su uso (variable X)
Al graficar los puntos, tenemos:
Ahora, si quisieramos ajustar un modelo que nos permita entender el comportamiento de los datos, podríamos ajustar una recta de la forma
Para modelar se requiere el concepto general de función, el cual se puede considerar que se refiere a una regla que asigna a cada elemento de un primer conjunto, un único elemento de un segundo conjunto.
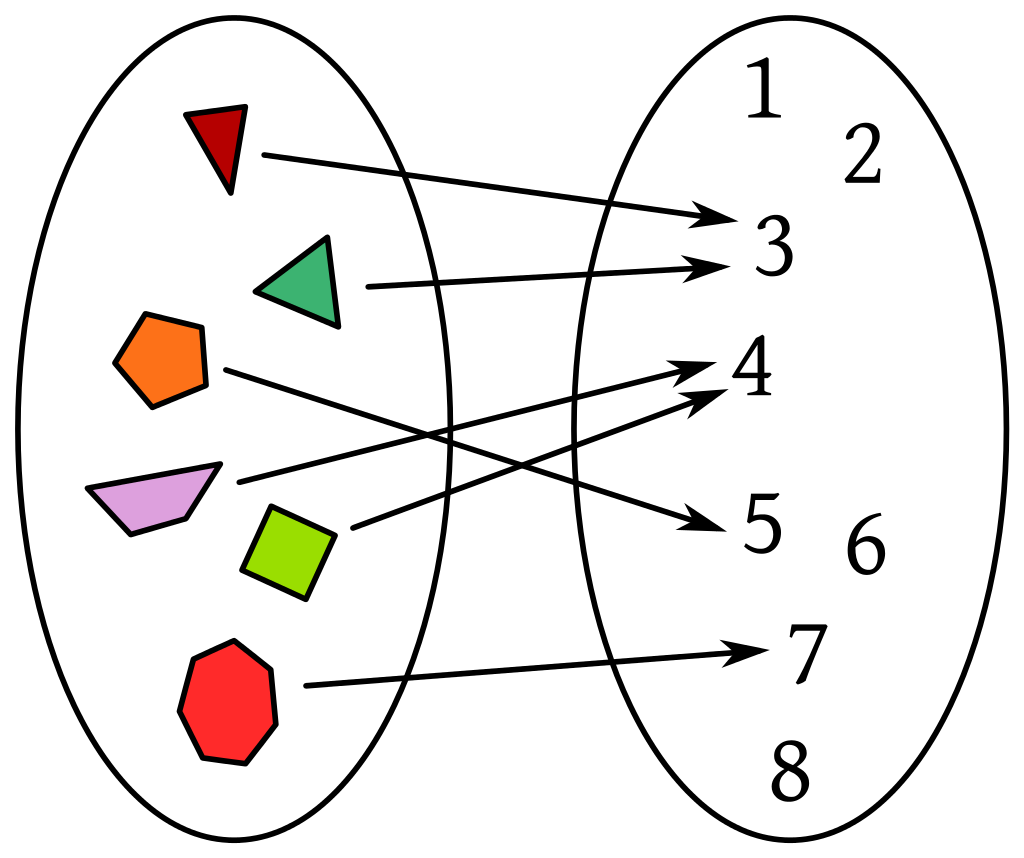
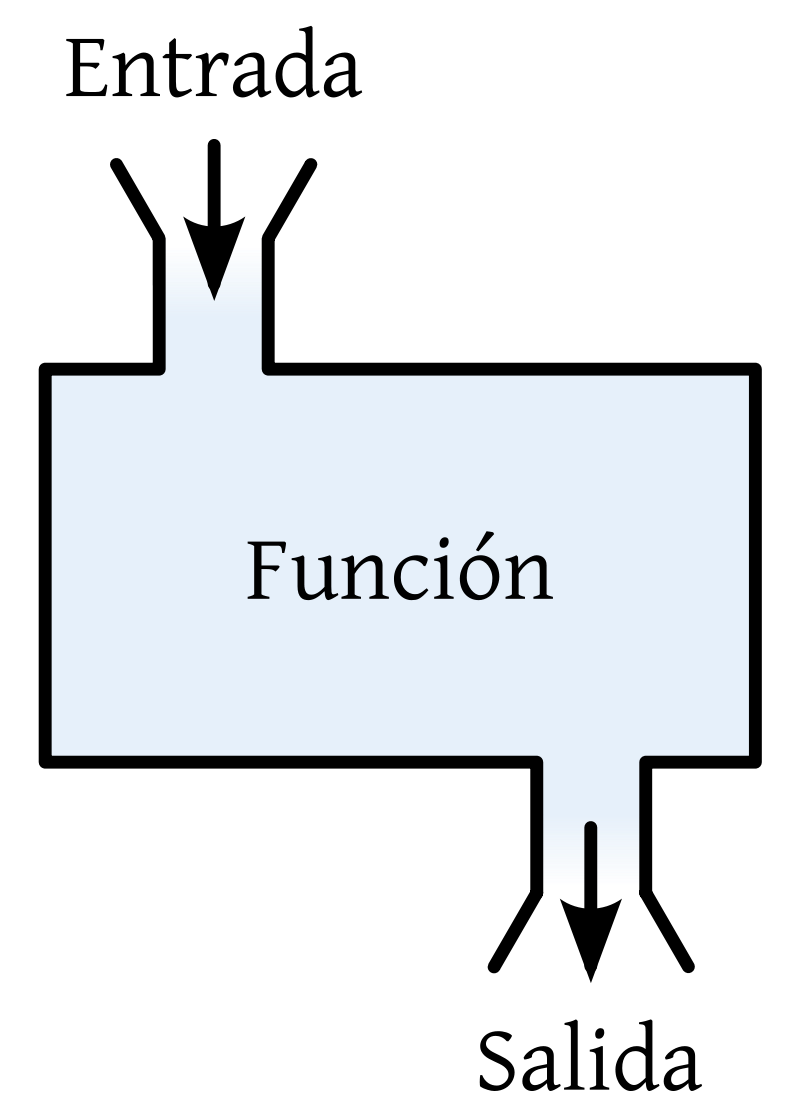
Una función también se puede ver como una “máquina”, en donde para cada “cosa” que entra, hay un procesamiento dentro de la máquina que nos arroja como resultado “una cosa” a la salida (dada por la relación entre los elementos del conjunto de entrada y los del conjunto de salida).
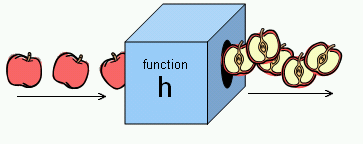
Por ejemplo, una “máquina” que corta manzanas se puede relacionar o ver como una función:
Entonces en nuestro caso, modelar es encontrar, mediante alguna técnica o metodología, una relación funcional entre una o más variables explicativas, predictoras, independientes o características (features) y una potencial variable de interés, respuesta, dependiente u objetivo (target), que puede que haya sido o no observada.
“Problema de regresión”:
Encontremos la f que generaliza la relación entre Y y X_1, X_2, \dots:
“Problema de clasificación”:
Encontremos la f que generaliza la relación entre Y y X_1, X_2, X_3, \dots:
“Problema de agrupamiento (asociación entre individuos)”:
Asignemos un grupo a cada instancia bajo algún criterio, es decir encontremos una Y categórica a partir de los valores que toman X_1, X_2, X_3, \dots (con la f que las relaciona):
“Problema de reducción de la dimensión (asociación entre variables)”:
¿Aprendizaje?
On February 24, 1956, Arthur Samuel’s Checkers program, which was developed for play on the IBM 701, was demonstrated to the public on television. In 1962, self-proclaimed checkers master Robert Nealey played the game on an IBM 7094 computer. The computer won. Other games resulted in losses for the Samuel Checkers program, but it is still considered a milestone for artificial intelligence, and offered the public in the early 1960s an example of the capabilities of an electronic computer. <www.ibm.com>
“Machine learning refers to the use of formal structures (machines) to do inference (learning).” Clarke, B., Fokoue, E. & Zhang, H.H., (2009). Principles and theory for data mining and machine learning.
“…Vast amounts of data are being generated in many fields, and the statistician’s job is to make sense of it all: to extract important patterns and trends, and understand ‘what the data says’. We call this learning from data.” Friedman, J., Hastie, T. & Tibshirani, R., (2009). The elements of statistical learning.
Usando programación “clásica” o “tradicional”:
Al computador le damos explícitamente un algoritmo asociado a lo que hace una función dada f, de modo que, cuando le demos un valor x, este nos dé el valor de y tal que y = f(x).
Aprendizaje supervisado:
Al computador le damos “muchos” x_i (features) y y_i (target), \left(x_i, y_i\right), para que este nos dé una función f tal que y_i = f(x_i) \left(y_i - f(x_i) = 0\right) para todo i, pero que a su vez se le pueda dar un valor no dado x_0, para quien no tenemos y_0, y que el computador nos “prediga” cuál debería ser el valor de ese y_0.
En este caso, la “predicción” suele ser el objetivo principal. Se busca resolver problemas de regresión (las y_i son valores de una variable cuantitativa) o de clasificación (las y_i son valores de una variable cualitativa). Todos los modelos del modelado estadístico que se puedan usar para “predecir” y’s se considerarían máquinas de aprendizaje supervisado.
Aprendizaje no supervisado:
Al computador le damos “muchos” x_i, para que nos dé f y y_i tal que y_i = f(x_i) \left(y_i - f(x_i) = 0\right) para todo i.
En este caso, el objetivo es explorar los datos (Exploratory Data Analysis) para identificar patrones (Pattern Recognition), extraer conocimiento (Knowledge Discovery) o realizar lo que en algún momento se denominó minería de datos (Data Mining). Es decir, se desea producir y’s que capturen, representen o reflejen, por ejemplo, la asociación entre variables o la asociación entre individuos. Las técnicas de estadística descriptiva multivariada para la reducción de la dimensión y para el agrupamiento (clustering) harían parte del aprendizaje no supervisado.
Máquina de aprendizaje
Consideremos el ejemplo de reconocimiento de dígitos escritos a mano.
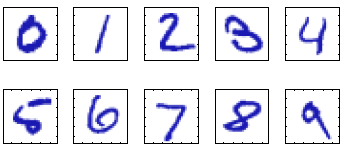
Cada dígito corresponde a una imagen de 28 \times 28 pixeles y, por lo tanto, puede representarse mediante un arreglo x que contiene 784 números entre 0 y 255 (o entre 0 y 1). El objetivo es obtener una función que tome un vector x como entrada y que produzca la identidad del dígito (0, \dots, 9) como salida.
Para definir una máquina de aprendizaje es necesario tener en cuenta que desde el comienzo tenemos un espacio de entrada, digamos \mathcal{X}, en el cual están los objetos a los cuales se les desea hacer una asignación de un objeto que está en otro espacio de salida, que vamos a denotar \mathcal{Y}. La definición de los dos espacios depende del problema.
Una máquina de aprendizaje es una función f que asocia a cada elemento de \mathcal{X} un único elemento en \mathcal{Y}. Escribiremos
f : \mathcal{X} \to \mathcal{Y}
Si x es un elemento del espacio \mathcal{X}, escribimos x\in\mathcal{X}, entonces la notación y = f(x), significa que y es el único elemento de \mathcal{Y} asociado a x.
En este ejemplo, el espacio de entrada \mathcal{X} es el conjunto de todos los arreglos de tamaño 28 \times 28, cuyos valores están en el intervalo [0,255]. Este espacio es finito, pero muy grande: 256^{56}.
Adicionalmente, el conjunto de salida \mathcal{Y} es el conjunto de etiquetas \{0,1,2,3,4,5,6,7,8,9,0\}.
Entrenamiento de una máquina de aprendizaje
La construcción de una máquina de aprendizaje requiere encontrar valores para un conjunto de parámetros que definan de manera específica a la función f, es decir, encontrar \hat{\theta} \in \Theta tal que f = f_{\hat{\theta}} \in \left\{ f_\theta: \theta \in \Theta \right\} \left(y = f(x) = f_{\hat{\theta}}(x) = f\left(x;\hat{\theta}\right)\right). El proceso de encontrar tales parámetros se conoce como entrenamiento o aprendizaje de la máquina. Es decir el entrenamiento consiste en encontrar (estimar) valores para tal conjunto de parámetros.
El entrenamiento de una máquina de aprendizaje es una forma de modelado. Básicamente el proceso de entrenamiento utiliza un conjunto de datos del espacio de entrada y las etiquetas o valores asociados en el conjunto de salida.
Conjunto de entrenamiento
Al adoptar un enfoque de aprendizaje de máquinas, el conjunto de dígitos (datos) utilizado para entrenar la máquina de aprendizaje es llamado un conjunto de entrenamiento.
Valores o etiquetas objetivo (target)
Las categorías (etiquetas) de los dígitos en el conjunto de entrenamiento se conocen de antemano, generalmente ya se revisaron y se etiquetaron manualmente. Podemos expresar la etiqueta de un dígito usando un arreglo objetivo que representa la identidad del dígito correspondiente.
Codificación one-hot
En el párrafo anterior parece extraño mencionar que en la salida hay un arreglo. En realidad, cuando se tienen varias etiquetas no numéricas, es conveniente recodificar las etiquetas usando arreglos binarios.
Esto se hace de la siguiente manera. Si se tiene p etiquetas, digamos 10 en el caso de los dígitos, entonces las etiquetas se convierten en arreglos unidimensionales de tamaño p, en donde todos los elementos son cero excepto en la posición que corresponde a la etiqueta que representa.
La siguiente tabla ilustra la codificación one-hot en el caso de los dígitos.
| dígito | one-hot |
|---|---|
| 0 | 1000000000 |
| 1 | 0100000000 |
| 2 | 0010000000 |
| 3 | 0001000000 |
| 4 | 0000100000 |
| 5 | 0000010000 |
| 6 | 0000001000 |
| 7 | 0000000100 |
| 8 | 0000000010 |
| 9 | 0000000001 |
La codificación one-hot es utilizada cuando se tienen variables categóricas. Esta es una forma en la cual datos categóricos y datos numéricos pueden interactuar. Por ejemplo, si una variable en el espacio de entrada es color, y hay digamos 3 colores: rojo, verde y azul, entonces la codificación one-hot puede ser
| color | one-hot |
|---|---|
| rojo | 100 |
| verde | 010 |
| azul | 001 |
En este caso, la variable de entrada color es reemplazada por las tres columnas de la codificación one-hot.
Algoritmo de entrenamiento
Los algoritmos de entrenamiento de máquinas de aprendizaje consisten básicamente en procesos de optimización de una función objetivo, que denominaremos función de pérdida.
Por ejemplo, supongamos que los valores objetivo \{y_1,\ldots,y_n\} de la máquina de aprendizaje son números reales y que los datos de entrenamiento son digamos \{x_1,\ldots, x_n\}.
En cada paso del proceso de entrenamiento, la función f calculada en x_i entrega un valor digamos \tilde{y}_i. Este valor en principio es diferente de y_i, debido a que justamente estamos entrenando la máquina para que “aprenda” que f(x_i)=y_i. Entonces una función de pérdida se puede definir como sigue:
\mathcal{Loss} = \tfrac{1}{n}\sum_{i=1}^{n}(y_i - \tilde{y}_i)^2.
El propósito del algoritmo de entrenamiento es encontrar valores para \theta de un función f_{\theta}, que haga que la función \mathcal{Loss} alcance un mínimo.
Sin embargo, un algoritmo de aprendizaje puede que no encuentre un conjunto de parámetros que minimicen globalmente a la función de pérdida.
Capacidad de generalización
La capacidad de un máquina de aprendizaje para etiquetar correctamente nuevos ejemplos (no vistos antes por la máquina) se conoce como capacidad de generalización.
Buscamos máquinas con muy buena capacidad de generalización.
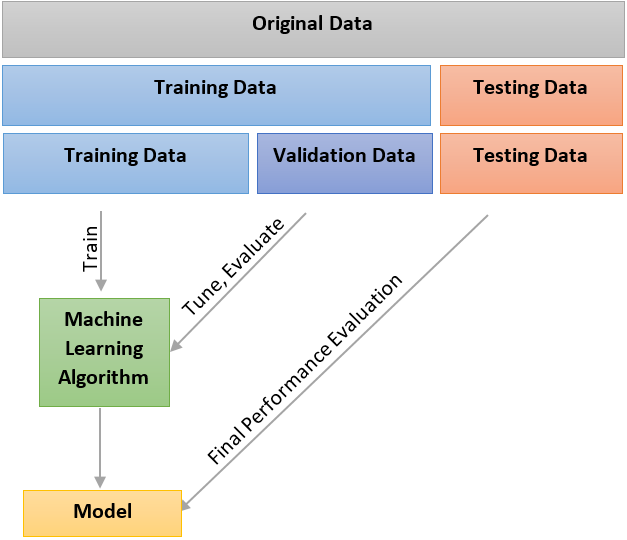
Conjunto de validación
La capacidad de generalización de una maquina de aprendizaje se evalúa con un conjunto de datos de entrada con sus respectivas etiquetas, que tengan la misma estructura de los datos de entrenamiento. Por ejemplo, si en el conjunto de datos de entrenamiento usamos 70,000 datos, es decir, 70,000 imágenes con sus respectivas etiquetas, entonces podríamos seleccionar 60,000 para entrenar a la máquina y en consecuencia 10,000 para la validación.
Extracción de características
Para la mayoría de las aplicaciones prácticas, las variables de entrada originales generalmente se preprocesan transformandolaes en un nuevo espacio de variables donde, se espera, que el reconocimiento de patrones sea más fácil de resolver (donde el algoritmo de entrenamiento funcione mejor).
Esta etapa de preprocesamiento es a veces también llamado extracción de características (feature extraction).
Tipos de aprendizaje
Aprendizaje supervisado
Aplicaciones en las que los datos de entrenamiento comprenden ejemplos de los arreglos de entrada junto con sus correspondientes arreglos objetivo se conocen como problemas de aprendizaje supervisado.
Casos como el ejemplo de reconocimiento de dígitos, en el que el objetivo es asignar a cada arreglo de entrada una etiqueta, se denominan problemas de clasificación.
Si la salida deseada consta de una o más variables continuas, entonces la tarea se llama regresión.
Aprendizaje no supervisado
En otros problemas los datos de entrenamiento consisten en un conjunto de arreglos de entrada que no tienen unos valores o etiquetas asociados. En este caso se consideran como problemas de aprendizaje no supervisado.
Los problemas de aprendizaje en los que se busca descubrir grupos de instancias o ejemplos (individuos o unidades estadísticas) similares dentro de los datos, se llaman problemas de agrupación (clustering).
Aprendizaje profundo
El aprendizaje profundo está basado en redes neuronales artificiales con múltiples capas (redes neuronales profundas). Mediante la optimización de funciones de pérdida, estas redes modelan relaciones complejas entre espacios complejos como los requeridos en aplicaciones de visión por computadora o de procesamiento de lenguaje natural.
Aprendizaje por refuerzo
El aprendizaje por refuerzo es un tipo de aprendizaje automático donde un “agente” aprende a tomar decisiones mediante “ensayo y error”, recibiendo “recompensas” o “castigos” según sus acciones, mientras busca maximizar una recompensa global a lo largo del tiempo.
Inteligencia artificial (Artificial Intelligence, AI) y aprendizaje automático (Machine Learning, ML)
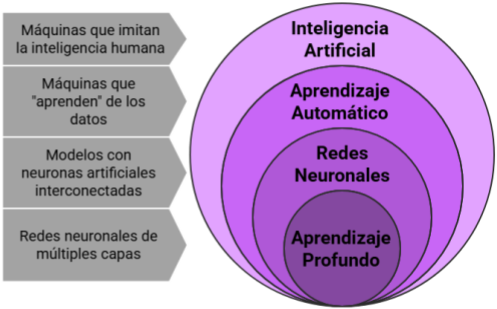
Quizá el primer paso debería ser leer y reflexionar sobre todo lo escrito al respecto, comenzando por TURING (1950) (o incluso desde Turing (1937)).
IA:
Diseñar sistemas capaces de realizar tareas, consideradas “inteligentes”, de forma autónoma.
Un agente inteligente puede ser definido como un sistema que percibe su entorno y toma acciones que maximizan sus probabilidades de éxito.
ML:
Programas que pueden mejorar su desempeño automáticamente.
“Aprenden” a partir de datos observados y generalizan a datos no vistos.
Turing, A. M. 1937. «On Computable Numbers, with an Application to the Entscheidungsproblem». Proceedings of the London Mathematical Society s2-42 (1): 230-65. https://doi.org/https://doi.org/10.1112/plms/s2-42.1.230.
TURING, A. M. 1950. «I.—COMPUTING MACHINERY AND INTELLIGENCE». Mind LIX (236): 433-60. https://doi.org/10.1093/mind/LIX.236.433.