3 Fundamentación matemático-estadística
3.1 Modelar
El primer modelo matemático existente podría considerarse como la abstracción de los números para aprender a contar. En este modelo, la idea era poder representar los objetos de la vida cotidiana como símbolos (en lo posible fáciles de manipular) para poder aumentar nuestra capacidad de cálculo y por lo tanto el poder de predecir.
Nuestro objetivo principal dentro del modelado es la “descripción” y/o la “predicción”. Partimos de unas hipótesis que nos permiten de alguna manera ver el problema de manera más sencilla y así obtener conclusiones válidas del tema estudiado. Advertencia: Es muy importante tener muy claras las hipótesis sobre las que se está trabajando, ya que una hipótesis errónea puede llevar a falsas conclusiones.
Supongamos que la empresa produce lámparas LED y que el tiempo de vida útil de estas lámparas (variable Y) está relacionado con la cantidad de electricidad que pasa a través de ellas durante su uso (variable X)
Al graficar los puntos, tenemos:
Ahora, si quisieramos ajustar un modelo que nos permita entender el comportamiento de los datos, podríamos ajustar una recta de la forma
Para modelar se requiere el concepto general de función, el cual se puede considerar que se refiere a una regla que asigna a cada elemento de un primer conjunto, un único elemento de un segundo conjunto.
Una función también se puede ver como una “máquina”, en donde para cada “cosa” que entra, hay un procesamiento dentro de la máquina que nos arroja como resultado “una cosa” a la salida (dada por la relación entre los elementos del conjunto de entrada y los del conjunto de salida).
Por ejemplo, una “máquina” que corta manzanas se puede relacionar o ver como una función:
Entonces en nuestro caso, modelar es encontrar, mediante alguna técnica o metodología, una relación funcional entre una o más variables explicativas, predictoras, independientes o características (features) y una potencial variable de interés, respuesta, dependiente u objetivo (target), que puede que haya sido o no observada.
“Problema de regresión”:
Encontremos la f que generaliza la relación entre Y y X_1, X_2, \dots:
“Problema de clasificación”:
Encontremos la f que generaliza la relación entre Y y X_1, X_2, X_3, \dots:
“Problema de agrupación”:
Asignemos un grupo a cada instancia bajo algún criterio, es decir encontremos una Y categórica a partir de X_1, X_2, X_3, \dots (con la f que las relaciona):
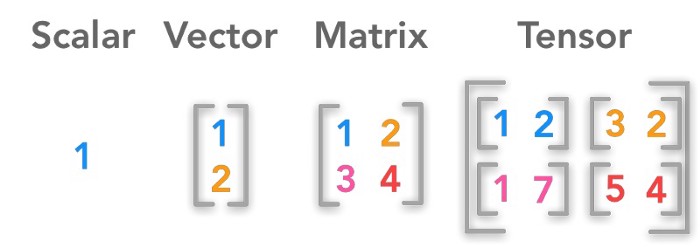
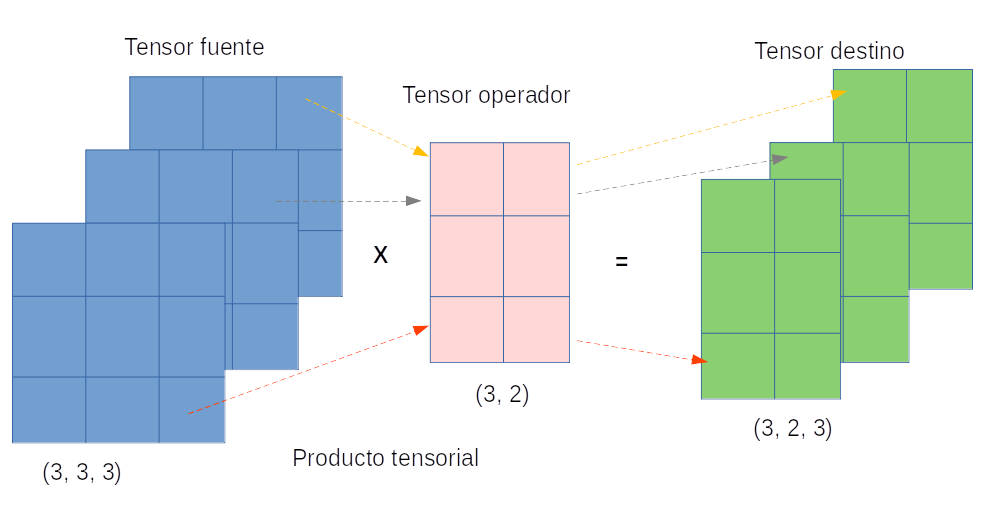
3.1.1 Teoremas de aproximación
3.1.1.1 Weierstrass
El teorema de aproximación de Weierstrass establece que cualquier función continua en un intervalo cerrado [a, b] puede ser aproximada de manera arbitrariamente precisa por un polinomio.
Teorema 3.1 Sea f: [a, b] \to \mathbb{R} una función continua. Entonces, para cualquier \epsilon > 0, existe un polinomio P(x) de coeficientes reales tal que:
\sup_{x \in [a, b]} |f(x) - P(x)| < \epsilon
Este resultado nos está diciendo que, en teoría, las funciones polinómicas son capaces de aproximar cualquier comportamiento de f en un intervalo cerrado. Además, el teorema tiene una demostración constructiva en donde se hace uso de los polinomios de Bernstein.
3.1.1.2 Stone-Weierstrass
Este teorema generaliza el resultado de Weierstrass y se aplica a subespacios de funciones continuas en espacios compactos. Permite la aproximación no solo con polinomios, sino con una clase más amplia de funciones. Es particularmente útil al permitir aproximaciones mediante combinaciones no lineales de funciones.
3.1.1.3 Kolmogorov-Arnold (Representación de funciones multivariadas)
El teorema de representación de Kolmogorov-Arnold establece que cualquier función continua de varias variables puede representarse como una suma finita de funciones continuas de una sola variable.
Teorema 3.2 Sea f: [0,1]^n \to \mathbb{R} una función continua. Entonces existe una representación de la forma:
f(x_1, \dots, x_n) = \sum_{q=0}^{2n} \varphi_q \left( \sum_{p=1}^n \psi_{q,p}(x_p) \right)
donde \varphi_q y \psi_{q,p} son funciones continuas de una sola variable.
En esencia, del teorema se podría concluir que la suma es la única función continua auténticamente multivariada. Esto debido a que cualquier otra función continua de varias variables puede expresarse en términos de sumas de funciones continuas de una sola variable.
3.1.1.4 Teorema de aproximación universal (redes neuronales de una capa oculta)
El teorema de aproximación universal es una extensión en el contexto de redes neuronales, indicando que una red neuronal de una sola capa oculta, con una cantidad suficiente de neuronas y funciones de activación no lineales adecuadas, puede aproximar cualquier función continua en un espacio compacto.
Teorema 3.3 Sea f: [a, b]^n \to \mathbb{R} una función continua en un espacio compacto. Entonces, para cualquier \epsilon > 0, existe una red neuronal de una capa oculta con una función de activación sigmoide \sigma y un conjunto de parámetros \theta = \{w_i, b_i\} tal que:
\left| f(x) - \sum_{i=1}^N c_i \, \sigma(w_i \cdot x + b_i) \right| < \epsilon \quad \forall x \in [a, b]^n
donde c_i \in \mathbb{R}, y N depende de \epsilon.
- ¿Qué otros teoremas de aproximación o representación existen?
- ¿Qué otras funciones (“máquinas”) podría utilizar como base para la aproximación?
- ¿Por qué esto es importante para lo que se está hablando acerca de modelar?
3.2 Algebra lineal y tensorial
El álgebra lineal es fundamental para el aprendizaje automático porque permite modelar y resolver problemas relacionados con la manipulación y transformación de datos a través de vectores y matrices. Su capacidad para describir relaciones lineales facilita la representación de datos y modelos.
Por su parte, el álgebra tensorial amplía esta capacidad al gestionar estructuras de datos más complejas que involucran múltiples dimensiones, proporcionando un marco para representar y operar sobre información de mayor orden. Esto es crucial en contextos donde los datos no pueden ser simplemente representados en espacios vectoriales o matriciales, sino que requieren una estructura más general para su procesamiento eficiente. Ambas ramas permiten una comprensión matemática profunda y la implementación de algoritmos de optimización necesarios para el ajuste de modelos.
Los arreglos son una estructura de datos que almacenan elementos de manera organizada y permiten el acceso a ellos mediante índices. Su relación con el álgebra lineal y tensorial radica en que los arreglos pueden ser considerados como representaciones computacionales de vectores, matrices y tensores.
3.3 Derivación
\lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x} = \frac{df}{dx} = f'(x)
Tasa o razón de cambio en un instante:
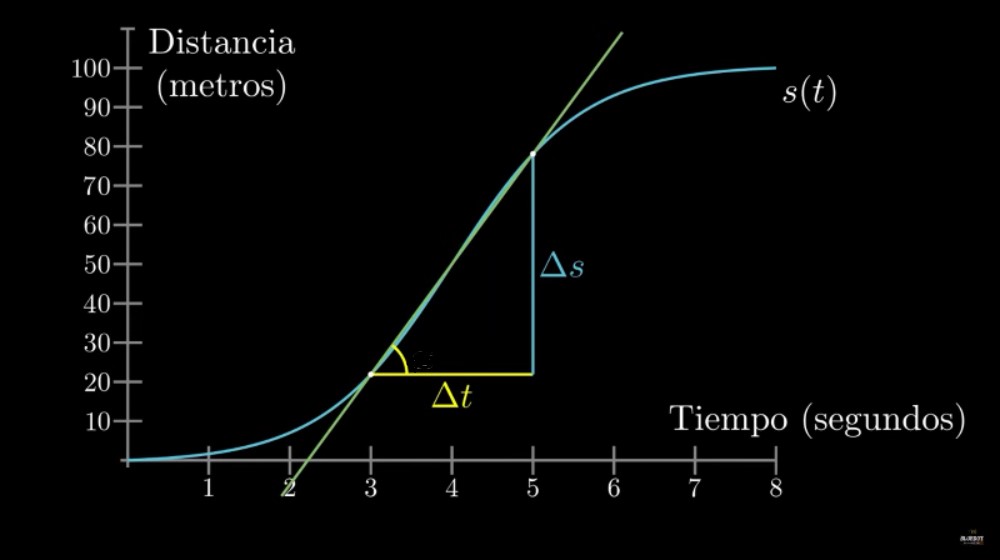
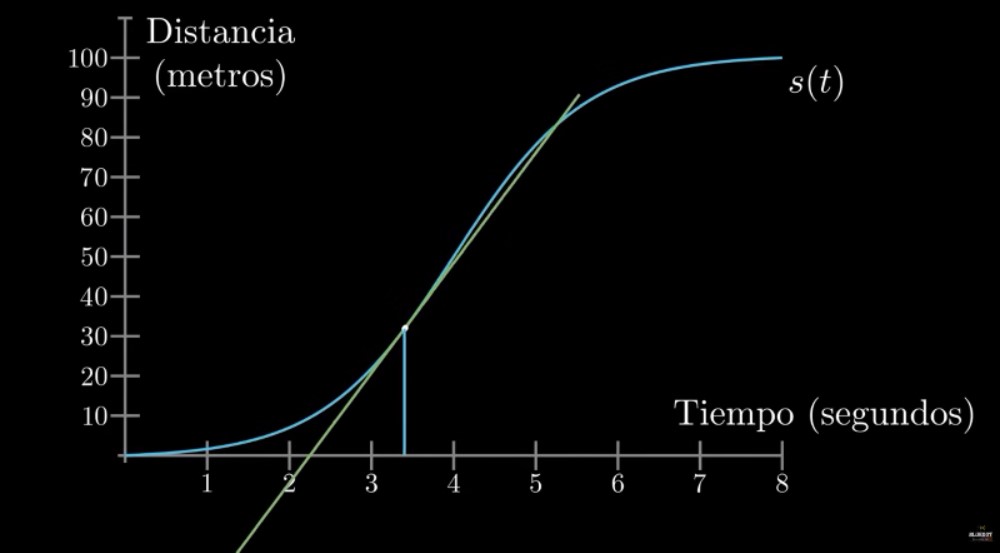
Pendiente de la recta tangente:
Aproximación lineal en el punto:
Nota
Aunque se sale del contexto de este curso, de pronto sería interesante el explorar desde la teoría, y luego desde la práctica, el impacto de introducir el uso de un concepto como el siguiente:
Las distribuciones, también conocidas como distribuciones de Schwartz o funciones generalizadas, son objetos que amplían la noción clásica de función en el análisis matemático. Las distribuciones permiten diferenciar funciones cuyas derivadas no existen en el sentido clásico. En particular, cualquier función localmente integrable tiene una derivada en el sentido de distribuciones.
Las distribuciones se utilizan ampliamente en la teoría de ecuaciones en derivadas parciales, donde puede ser más sencillo establecer la existencia de soluciones en el sentido de distribuciones (soluciones débiles) en lugar de soluciones clásicas, o donde las soluciones clásicas adecuadas pueden no existir. Las distribuciones también son importantes en física e ingeniería, ya que muchos problemas conducen naturalmente a ecuaciones diferenciales cuyas soluciones o condiciones iniciales son singulares, como en el caso de la función delta de Dirac.
Adaptado de: https://en.wikipedia.org/wiki/Distribution_(mathematics)
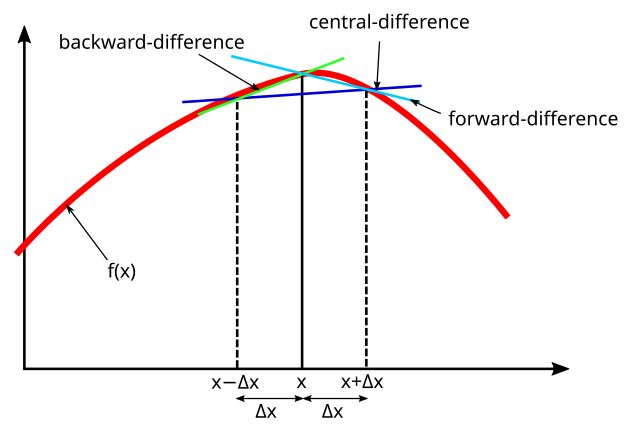
3.3.1 Diferenciación numérica
El computador no tiene forma de entender o procesar directamente el límite que se encuentra en la fórmula de la derivada. Por esta razón es necesario optar por un acercamiento numérico:
f'(x_i)\approx \frac{\Delta f }{\Delta x}\bigg|_{x_{i}}=\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}
Este procedimiento es conocido como diferencias finitas, y podría llegar a ser útil para solucionar ecuaciones diferenciales (ordinarias o parciales).
3.3.2 Diferenciación simbólica
En matemáticas y ciencias de la computación, el álgebra computacional, también llamada cálculo simbólico o cómputo algebraico, es un área científica que se refiere al estudio y desarrollo de algoritmos y software para manipular expresiones matemáticas y otros objetos matemáticos. Aunque el álgebra computacional podría considerarse un subcampo de la computación científica, generalmente se les considera campos distintos, ya que la computación científica se basa en el cálculo numérico con números de punto flotante aproximados, mientras que el cálculo simbólico enfatiza el cálculo exacto con expresiones que contienen variables sin un valor asignado y que se manipulan como símbolos.
En Python, para obtener \frac{d}{dx} \mathrm{e}^{x^2} mediante diferenciación simbólica, se puede hacer:
# pip install sympy
from sympy import *
x, y, z = symbols('x y z')
diff(exp(x**2), x)Para obtener \frac{\partial^7}{\partial x\partial y^2\partial z^4} \mathrm{e}^{x y z} mediante diferenciación simbólica, se puede hacer:
expr = exp(x*y*z)
diff(expr, x, y, y, z, z, z, z)Internamente, SymPy utiliza una serie de técnicas avanzadas de manipulación simbólica basadas en reglas algebraicas y patrones para obtener la derivada simbólica. El proceso a grandes rasgos incluye:
- Representación simbólica: SymPy primero convierte las expresiones en una estructura de datos simbólica.
- Aplicación de reglas de diferenciación: Una vez que la expresión está en forma simbólica, SymPy aplica reglas de diferenciación estándar. SymPy descompone la expresión en términos y factores, aplicando estas reglas recursivamente a cada componente.
- Simplificación paso a paso: SymPy usa técnicas de simplificación para evitar que la expresión resultante se vuelva innecesariamente compleja.
- Optimización de expresiones: SymPy aplica optimizaciones para minimizar el número de operaciones y mejorar la eficiencia. Por ejemplo, si detecta términos nulos o identidades como multiplicaciones por 1 o adiciones de 0, los elimina.
- Ensambla el resultado final: Finalmente, SymPy reconstruye la derivada completa como una nueva expresión simbólica exacta. Esta expresión puede manipularse, simplificarse aún más, o evaluarse en puntos específicos si se desea.
3.3.3 Diferenciación automática
La diferenciación automática se distingue de la diferenciación simbólica y la diferenciación numérica. La diferenciación simbólica enfrenta el desafío de convertir un programa de computadora en una única expresión matemática, lo que a menudo resulta en código ineficiente. La diferenciación numérica, que se basa en el método de diferencias finitas, puede introducir errores de redondeo y de cancelación debido al proceso de discretización. Ambas técnicas clásicas presentan dificultades para calcular derivadas de orden superior, en las que tanto la complejidad como los errores aumentan significativamente. Además, estos métodos clásicos suelen ser lentos para calcular derivadas parciales de funciones con respecto a múltiples variables, lo cual es esencial en algoritmos de optimización basados en gradientes. La diferenciación automática resuelve todos estos problemas de manera eficiente.
La diferenciación automática aprovecha el hecho de que todo cálculo en una computadora, por complejo que sea, se ejecuta como una secuencia de operaciones aritméticas elementales (suma, resta, multiplicación, división, etc.) y funciones básicas (exp, log, sin, cos, etc.). Al aplicar la regla de la cadena de manera repetida a estas operaciones, es posible calcular derivadas parciales de cualquier orden de forma automática y precisa, manteniendo la precisión de trabajo. Además, la diferenciación automática solo requiere, como máximo, un pequeño factor constante adicional de operaciones aritméticas en comparación con el programa original.
Ejemplo 3.1 Consideremos la función:
f(x) = \sin(x) + x^2
Queremos calcular la derivada de f(x) en x = 2 utilizando diferenciación automática en modo directo (forward mode).
-
Definir variables y derivadas iniciales:
Para aplicar diferenciación automática, asociamos a cada variable una pareja de valores: el valor de la función y el valor de su derivada. Inicialmente, tenemos la variable x con:
- Valor: x = 2
- Derivada: \dot{x} = 1 (ya que \frac{dx}{dx} = 1)
Entonces, representamos x como el par (x, \dot{x}) = (2, 1).
-
Calcular el valor y derivada de cada operación:
Descomponemos la función f(x) = \sin(x) + x^2 en operaciones elementales, desde luego, aplicando la regla de la cadena:
-
Calcular u = \sin(x):
- Valor: u = \sin(2) \approx 0.9093
- Derivada: \dot{u} = \cos(2) \cdot \dot{x} \approx -0.4161 \cdot 1 = -0.4161
Entonces, u = (0.9093, -0.4161).
-
Calcular v = x^2:
- Valor: v = 2^2 = 4
- Derivada: \dot{v} = 2x \cdot \dot{x} = 2 \cdot 2 \cdot 1 = 4
Por lo tanto, v = (4, 4).
-
Calcular f(x) = u + v:
- Valor: f(x) = 0.9093 + 4 = 4.9093
- Derivada: \dot{f} = \dot{u} + \dot{v} = -0.4161 + 4 = 3.5839
-
El valor de la función y su derivada en x = 2 son:
f(2) = 4.9093, \quad f'(2) = 3.5839
En Python, para obtener \frac{d^2}{dx^2} \tanh(x) mediante diferenciación automática, se puede hacer:
import numpy as np
import matplotlib.pyplot as plt
import jax.numpy as jnp
from jax import grad, jit, vmap
d2_tanh = jit(vmap(grad(grad(jnp.tanh))))
x = jnp.linspace(-5,5,100)
plt.figure(figsize=(6,4))
plt.plot(x, np.tanh(x))
plt.plot(x, d2_tanh(x))
plt.legend(["tanh","d2_tanh"], fontsize=15)
plt.grid()
plt.show()3.4 Optimización
La mayoría de los algoritmos en la ciencia de datos implican optimización de algún tipo. Por lo general, expresamos la mayoría de los problemas de entrenamiento de un modelo en la ciencia de datos, y en particular en la inteligencia artificial, en términos de minimizar una función, por ejemplo: h_{\theta}(X,Y).
\theta^* = \underset{\theta \in \Theta}{\operatorname{argmin}} h_{\theta}(X,Y) = \underset{\theta \in \Theta}{\operatorname{argmin}} h(\theta; X,Y).
La función que queremos minimizar se llama función o criterio objetivo. Cuando estamos minimizando, también podemos llamarla función de costo, función de pérdida o función de error.
La búsqueda de un mínimo global puede ser una tarea muy dura en aprendizaje de máquinas si se tiene en cuenta que las funciones pueden llegar a tener muchos parámetros y en consecuencia se tendría un espacio de muchas dimensiones.
Ejemplo 3.2 (Máxima verosimilitud) Exceptuando algunos casos especiales, las ecuaciones de verosimilitud, \frac{\partial }{\partial \theta} \mathrm{L}(\theta; x_1, \dots, x_n) = 0 \quad \text{ y } \quad \frac{\partial }{\partial \theta} \log \mathrm{L}(\theta; x_1, \dots, x_n) = 0, no pueden solucionarse de manera analítica. Por tanto, es necesario usar métodos numéricos o procedimientos iterativos para poder solucionar el problema de optimización asociado a dichas ecuaciones, \underset{\theta \in \Theta}{\arg \sup} \; \mathrm{L}\left(\theta; x_1, \dots, x_n \right) \quad \text{ y } \quad \underset{\theta \in \Theta}{\arg \sup} \; \log \mathrm{L}\left(\theta; x_1, \dots, x_n \right).
Existen variados métodos numéricos para resolver problemas de optimización. Buena parte de ellos toman un valor inicial para \theta, notado \hat{\theta}_0, y a partir de él buscan obtener una secuencia convergente \{ \hat{\theta}_r \}_{r=0,1,\dots}. Los algoritmos más comúnmente utilizados, los Hill climbing algorithms, se basan en una ecuación de actualización de este tipo, \hat{\theta}_{r+1} = \hat{\theta}_{r} + \lambda_r \; \mathbf{\mathrm{d}}_r\left(\hat{\theta}_r\right) donde el vector \mathbf{\mathrm{d}}_r\left(\hat{\theta}_r\right) indica la “dirección del r-ésimo paso” y el escalar \lambda_r representa la “longitud o tamaño de ese r-ésimo paso”.
En el caso de los Gradient ascent algorithms, la dirección de cada paso es la del gradiente de la función objetivo, \mathbf{\mathrm{d}}_r\left(\hat{\theta}_r\right) = \Delta \left(\hat{\theta}_r\right). El gradiente de la función de log-verosimilitud con respecto al vector de parámetros suele denominarse score, \Delta \left(\theta\right) = \frac{\partial}{\partial \theta} \log \mathrm{L}.
En el método de Newton–Raphson, \lambda_r = 1 y \mathbf{\mathrm{d}}_r\left(\hat{\theta}\right) = -\mathbf{\mathrm{H}}^{-1}\left(\hat{\theta}_r\right) \Delta\left(\hat{\theta}_r\right), donde \Delta(\theta) es el score y \mathbf{\mathrm{H}}^{-1}(\theta) es el inverso de la matrix Hessiana de la función de log-verosimilitud \left( \mathbf{\mathrm{H}}(\theta) = \frac{\partial^2}{\partial \theta \partial \theta^T} \log \mathrm{L} \right), ambos evaluados en \hat{\theta}_r.
El método denominado Fisher’s Scoring es casi idéntico al método de Newton-Raphson, pero en vez de utilizar el negativo del inverso de la matrix Hessiana de la función de log-verosimilitud \left(-\mathbf{\mathrm{H}}^{-1}(\theta) \right), utiliza el inverso de la matriz de información de Fisher \left(\mathcal{I}^{-1}\left(\theta\right) \right). La matriz de información de Fisher es la varianza del score, \mathcal{I}\left(\theta\right) = Var \left[ \Delta\left(\theta\right) \right] = E \left[ \Delta\left(\theta\right) \Delta\left(\theta\right)^T \right] y bajo ciertas condiciones (condiciones de regularidad), también es igual al inverso aditivo del valor esperado de la matriz Hessiana de la función de log-verosimilitud, \mathcal{I}\left(\theta\right) = Var \left[ \Delta\left(\theta\right) \right] = E \left[ \Delta\left(\theta\right) \Delta\left(\theta\right)^T \right] = - E \left[ \mathbf{\mathrm{H}}(\theta) \right].
3.4.1 Optimización basada en gradiente
El problema de entrenar una máquina es un problema de optimización.
Para que el concepto de “minimización” tenga sentido, debe haber una sola salida (función escalar).
El gradiente generaliza la noción de derivada al caso en que la derivada es con respecto a una dirección en el espacio. El gradiente de f, denotado \nabla_\theta h(\theta), es el vector que contiene todas las derivadas parciales. El elemento i del gradiente es la derivada parcial de h con respecto a \theta_i.
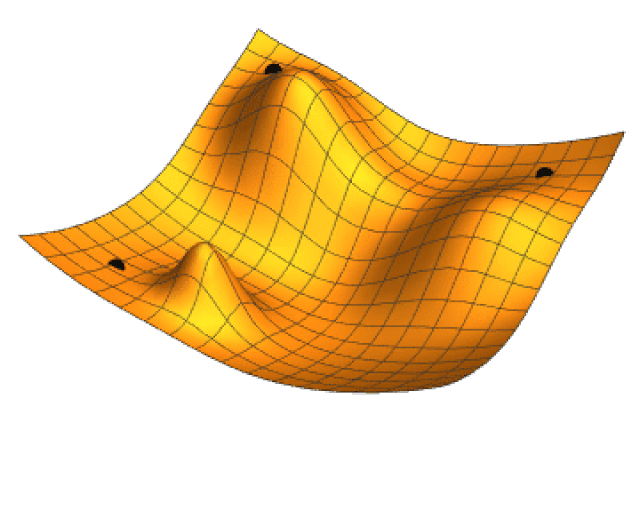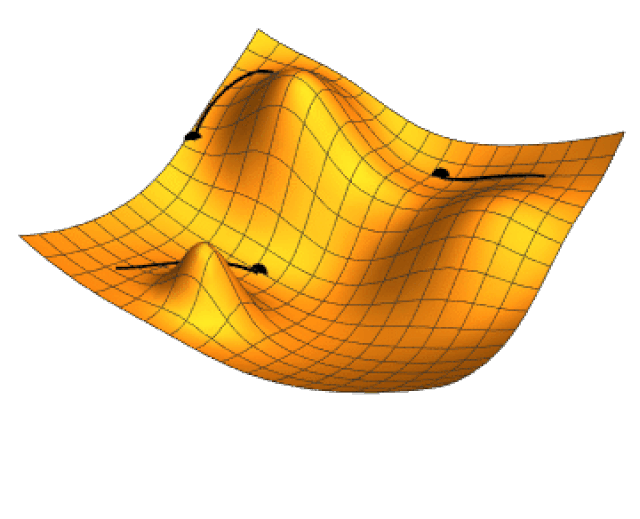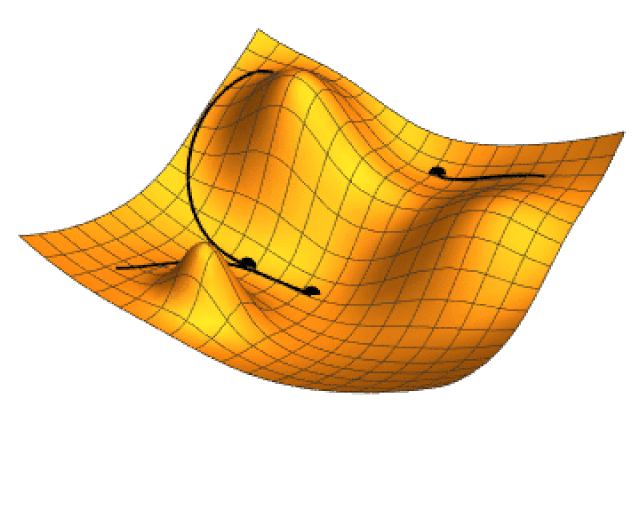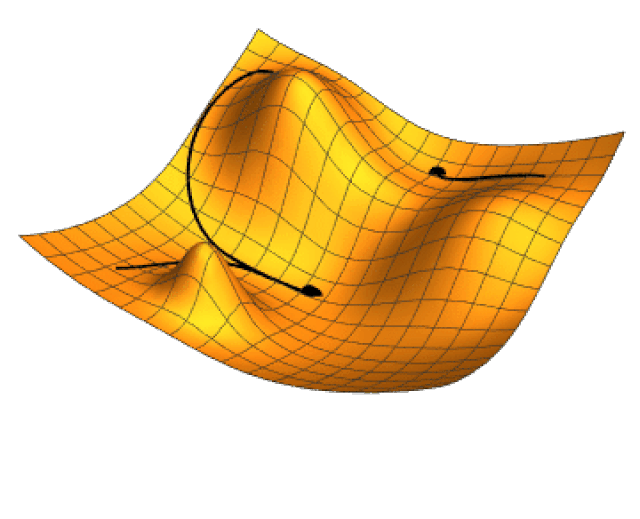
En múltiples dimensiones, los puntos críticos son puntos donde cada elemento del gradiente es igual a cero. Por otro lado, se puede verificar que el gradiente \nabla_\theta h(\theta) es ese vector que apunta en la dirección en la cual la función h crece más rápidamente partiendo precisamente del punto \theta. En consecuencia, -\nabla_\theta h(\theta) apunta en la dirección contraria, es decir en la dirección hacia la cual la función decrece más rápido, desde el punto \theta. Esta es la clave de los métodos de optimización basados en el gradiente.
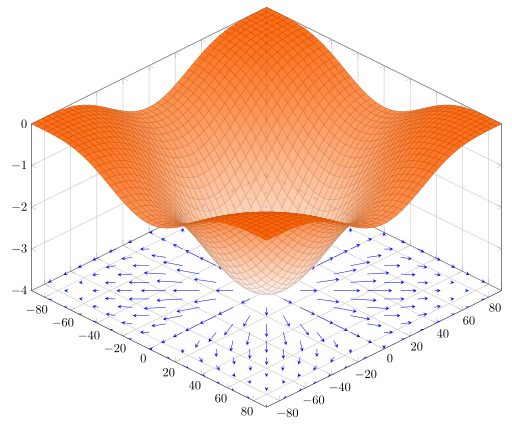
La siguiente imagen ilustra el gradiente proyectado en el plano \theta_1 \theta_2 de la función h(\theta_1,\theta_2)= -(\cos \theta_1^2 + \sin \theta_2^2)^2.
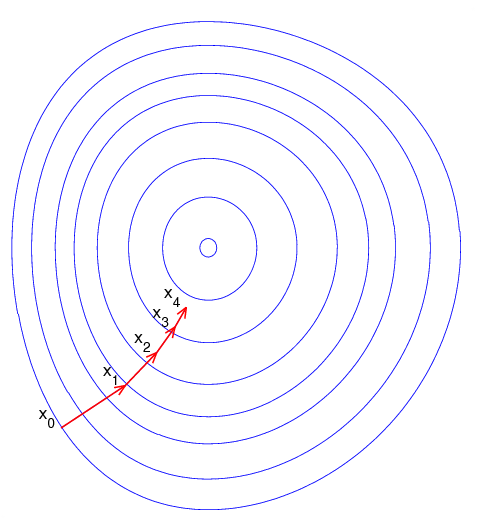
El término gradiente descendiente indica que se usará -\nabla_\theta f (\theta) para moverse a un siguiente punto en busca de un mínimo local. El método general se escribe como:
\theta^{(k+1)} = \theta^{(k)} − \eta_{k} \nabla_\theta \, f\left(\theta^{(k)}\right)
Los valores \eta_k se denominan genéricamente tasa de aprendizaje. La razón de incorporar la tasa de aprendizaje es controlar el tamaño de paso. Si no hace esta corrección podemos alejarnos en lugar de acercarnos al mínimo que se está buscando. La siguiente imagen animada muestra como opera la técnica de gradiente descendiente en un función de dos variables.
3.4.1.1 Gradiente descendiente en lote
En el método de gradiente descendiente básico, también conocido como descenso de gradiente por lotes, calcula el gradiente de la función de pérdida con respecto a los parámetros \boldsymbol{\theta} para el conjunto de datos de entrenamiento completo (\mathbf{x}_{train},\mathbf{y}_{train}). Si \mathfrak{L} es la función de pérdida del problema, entonces se tiene que
\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \eta_k \, \nabla_{\boldsymbol{\theta}} \, \mathfrak{L}(\boldsymbol{\theta}_k;\mathbf{x}_{train},\mathbf{y}_{train}),
El principal problema a resolver con los métodos de gradiente descendiente es cómo definir y actualizar en cada paso la tasa de aprendizaje \eta_k. Un fragmento de código, en el cual se actualiza la tasa de aprendizaje podría lucir como sigue. Supongamos que al comenzar 0<\eta_0<1.
def gd(theta, x_train, y_train, loss_func, epochs):
for i in range(epochs):
gradient = evaluate_gradient(loss_func, x_train, y_train, theta)
theta -= eta * gradient
eta *= eta
return theta, gradient3.4.1.2 Gradiente descendiente estocástico
El descenso de gradiente estocástico (SGD), por el contrario, realiza una actualización de parámetros para cada ejemplo de entrenamiento x_{train}^{(i)} y etiqueta y_{train}^ {(i)}, seleccionados al azar en cada época.
\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \eta_k \, \nabla_{\boldsymbol{\theta}} \, \mathfrak{L}\left(\boldsymbol{\theta}_k, {x}_{train}^{(i)},{y}_{train}^{(i)}\right),
En el artículo original de Robbins and Monro (1951) \eta cambia en cada iteración como acabamos de mostrar y se asume que \{\eta_k\} es una sucesión tal que \sum_k \eta_k = \infty, and \sum_k \eta_k^2 < \infty. Por ejemplo, se puede escoger \eta_k = 1/k. Robbins y Monro demostraron que bajo condiciones muy generales este algoritmo converge a la solución de problema, con probabilidad 1.
Un fragmento de código del algoritmo de Robbins and Monro podría lucir como sigue.
def sgd(theta, data_train, loss_func, epochs):
for i in range(epochs):
np.random.shuffle(data)
for example in data:
x, y = example
gradient = evaluate_gradient(loss_func,x, y, theta )
theta = theta - eta * gradient
eta *= eta
return theta, gradient3.4.1.3 Gradiente descendiente estocástico por mini-lotes
El descenso de gradiente por mini-lotes finalmente toma lo mejor de los dos mundos anteriores y realiza una actualización para cada mini-lote de n ejemplos de entrenamiento:
\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \eta_k \, \nabla_{\boldsymbol{\theta}} \, \mathfrak{L}\left(\boldsymbol{\theta}_k;\mathbf{x}_{train}^{(i:i+n)},\mathbf{y}_{train}^{(i:i+n)}\right),
En adelante se asumirá que tomamos mini-lotes, por lo que se omitirán en todas las expresiones los súper-índices para los datos (\mathbf{x}_{train}^{(i:i+n)},\mathbf{y}_{train}^{(i:i+n)}).
Un fragmento de código para este método podría lucir como sigue:
def sgd_mini_batch(theta, data_train, loss_func, epochs, batch_size):
for i in range(epochs):
np.random.shuffle(data_train)
for batch in get_batches(data_train, batch_size = batch_size):
x, y = batch
gradient = evaluate_gradient(loss_func, x, y, theta)
theta -= eta * gradient
eta *= eta
return theta, gradientEl tamaño de los mini-lotes depende del problema y puede ser 32, 64, 128, etc. En el ejemplo, get_batches() es una función generadora que va entregando lotes de datos a la medida que el algoritmo los requiere. Para las TPU se esperan mini-lotes de tamaño que sea múltiplo de 128.
El método de descenso de gradiente estándar presenta desafíos significativos en cuanto a la convergencia y requiere ciertos ajustes:
Elección de la tasa de aprendizaje: Seleccionar una tasa de aprendizaje adecuada puede ser complejo. Una tasa de aprendizaje demasiado baja lleva a una convergencia extremadamente lenta, mientras que una tasa demasiado alta puede dificultar la convergencia, haciendo que la función de pérdida fluctúe alrededor del mínimo o incluso diverja.
Ajustes de la tasa de aprendizaje: Las estrategias de ajuste de la tasa de aprendizaje buscan modificarla a lo largo del entrenamiento, ya sea reduciéndola según una idea o un plan predefinido o cuando el cambio en la función de pérdida entre épocas cae por debajo de cierto umbral. Sin embargo, estos planes y umbrales deben fijarse de antemano, lo cual limita su capacidad para adaptarse a las características específicas de un conjunto de datos.
Aplicación uniforme de la tasa de aprendizaje: En el descenso de gradiente tradicional, se utiliza la misma tasa de aprendizaje para todas las actualizaciones de parámetros. Sin embargo, en situaciones donde los datos son escasos o las frecuencias de las variables (características) varían ampliamente, podría ser preferible aplicar una actualización mayor para las características que ocurren con menos frecuencia y una menor para las que son más comunes.
Manejo de funciones no convexas: Al minimizar funciones de pérdida altamente no convexas, como suele ser el caso en redes neuronales, otro desafío es evitar quedar atrapado en mínimos locales subóptimos. Algunos estudios sugieren que la dificultad principal no está en los mínimos locales, sino en los puntos de silla: puntos donde una dimensión de la función se inclina hacia arriba y otra hacia abajo. Estos puntos suelen estar rodeados por mesetas con el mismo valor de error, lo que dificulta que el SGD los escape, ya que el gradiente es cercano a cero en todas las dimensiones.
Para una revisión contemporáneas de los algoritmos de optimización modernos puede consultar An overview of gradient descent optimization algorithms.
3.4.1.4 Método del momento
SGD tiene problemas para navegar por los barrancos, es decir, áreas donde la superficie se curva mucho más abruptamente en una dimensión que en otra, que son comunes en los óptimos locales. En estos escenarios, SGD oscila a lo largo de las pendientes del barranco mientras solo avanza vacilante por el fondo hacia el óptimo local.
El método del momento ayuda a acelerar SGD en la dirección relevante y amortigua oscilaciones. Lo hace sumando una fracción \lambda del vector de actualización del paso anterior al vector de actualización actual.
El método se esquematiza como sigue
\begin{align} \mathbf{v}_k &= \lambda \mathbf{v}_{k-1} + \eta \, \nabla_{\boldsymbol{\theta}} \, \mathfrak{L}\left(\boldsymbol{\theta}_k;{x}_{train}^{(i)},{y}_{train}^{(i)},\right)\\ \theta_{k+1} &= \theta_{k} - v_k, \end{align} \lambda<1. Usualmente, \lambda= 0.9.
3.4.1.5 RMSprop
Desarrollado por Goeff Hinton, no publicado. Se basa en dividir la tasa de aprendizaje en cada paso por un promedio del cuadrado de las componentes del gradiente en el paso anterior, por cada componente \theta del vector de parámetros \boldsymbol{\theta}.
Sea g una componente genérica del gradiente asociada a \theta, entonces el método RMSprop es como sigue:
- E[g^2]_t= \lambda E[g^2]_{t-1} + (1-\lambda)g_t^2
- \theta_{t+1} = \theta_t - \tfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}}g_t
\epsilon >0 es para evitar divisiones por cero.
Las operaciones indicadas se realizan componente a componente.
- \lambda es el parámetro de decaimiento. Típicamente \lambda = 0.9.
- \eta es la tasa de aprendizaje. Típicamente el valor por defecto es 0.001.
3.4.1.6 Algoritmo Adam
El algoritmo Adam a method for Stochastic optimization de Kingma y Lei es actualmente el método más utilizado.