4 Programación estructurada
En esta sección se hará una revisión de lo que es la programación estructurada.
En esta revisión se hace mención al control del flujo de un algoritmo/programa mediante estructuras de secuencia, selección y repetición.
Así mismo, se espera que al finalizar las actividades de esta sección, el estudiante tenga clara la manera en que se hace el diseño de un algoritmo bajo el paradigma de programación imperativa estructurada, ya sea mediante el uso de un diagrama de flujo o de pseudocódigo.
4.1 ¿Qué es la programación estructurada?
La programación estructurada es un conjunto de técnicas para desarrollar algoritmos fáciles de escribir, verificar, leer y modificar. La programación estructurada utiliza:
- Diseño descendente. Consiste en diseñar los algoritmos en etapas, yendo de los conceptos generales a los de detalle. El diseño descendente se verá completado y ampliado con el diseño modular.
- Recursos abstractos. En cada descomposición de una acción compleja se supone que todas las partes resultantes están ya resueltas, posponiendo su realización para el siguiente refinamiento.
- Estructuras básicas. Los algoritmos deberán ser escritos utilizando únicamente tres tipos de estructuras básicas (secuencia, selección y repetición).
4.2 Teorema de Böhm y Jacopini
Para que la programación sea estructurada, los programas han de ser propios. Un programa se define como propio si cumple las siguientes características:
- Tiene un solo punto de entrada y uno de salida.
- Cada acción del algoritmo es accesible, es decir, existe al menos un camino que va desde el inicio, pasa por la acción y llega hasta el fin del algoritmo.
- No tiene bucles infinitos.
El teorema de Böhm y Jacopini (Böhm y Jacopini 1966) dice que: “un programa propio puede ser escrito utilizando únicamente tres tipos de estructuras: secuencial, selectiva y repetitiva”. De este teorema se deduce que se han de diseñar los algoritmos empleando exclusivamente dichas estructuras, la cuales, como tienen un único punto de entrada y un único punto de salida, harán que nuestros programas sean propios.
4.3 Control del flujo de un programa
El flujo (orden en que se ejecutan las sentencias de un programa) es secuencial si no se especifica otra cosa. Este tipo de flujo significa que las sentencias se ejecutan en secuencia, una después de otra, en el orden en que se sitúan dentro del programa. Para cambiar esta situación se utilizan las estructuras que permiten modificar el flujo secuencial del programa. Así, las estructuras de selección se utilizan para seleccionar las sentencias que se han de ejecutar a continuación y las estructuras de repetición (repetitivas o iterativas) se utilizan para repetir un conjunto de sentencias.
4.3.1 Estructura secuencial
Una estructura secuencial es aquella en la cual una acción se ejecuta detrás de otra. El flujo del programa coincide con el orden físico en el que se sitúan las instrucciones:
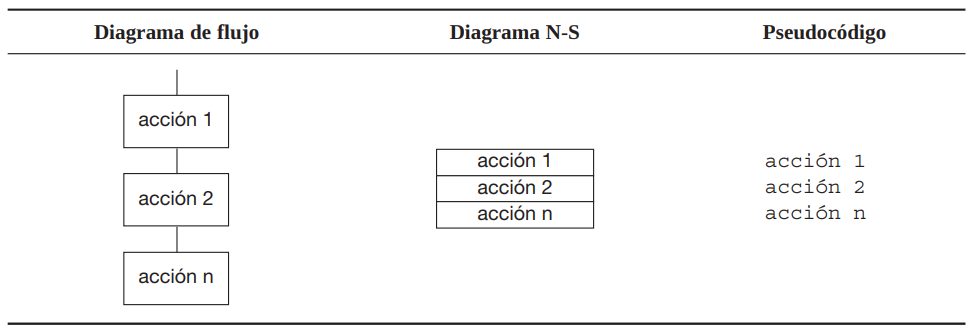
4.3.2 Estructura selectiva
Una estructura selectiva es aquella en que se ejecutan unas acciones u otras según se cumpla o no una determinada condición.
Cuando el resultado de evaluar la condición es verdad se ejecutará una determinada acción o grupo de acciones y si el resultado es falso se ejecutará otra acción o grupo de acciones diferentes:
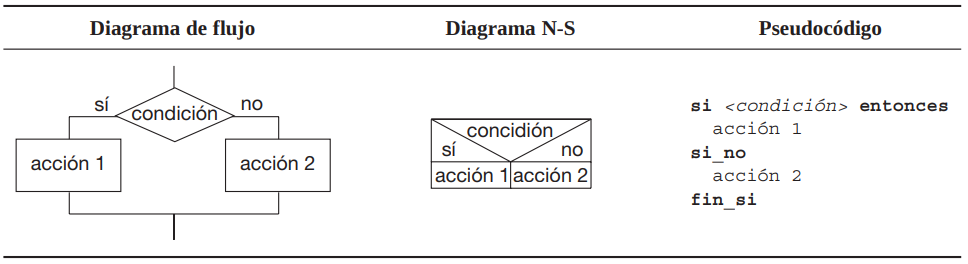
Si no es necesario ejecutar una determinada acción o acciones cuando el resultado es falso entonces se usa una versión simplificada o reducida de la anterior estructura selectiva:
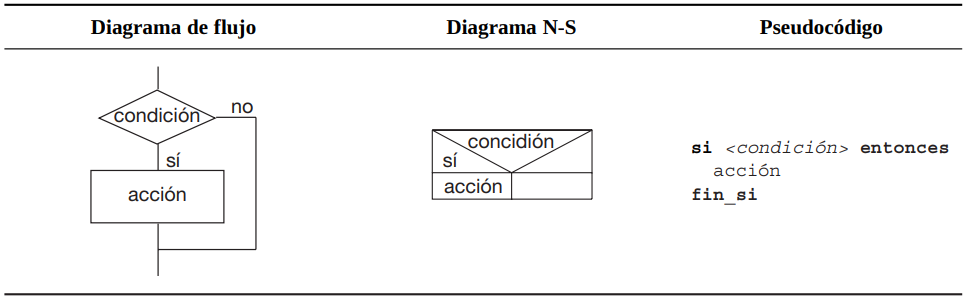
En este último caso, también se puede decir que cuando la condición es verdad se ejecutará una determinada acción o grupo de acciones y si el resultado es falso simplemente no se ejecutará.
4.3.3 Estructura iterativa
Las acciones del cuerpo de la estructura iterativa se repiten mientras o hasta que se cumpla una determinada condición. Es frecuente el uso de contadores o banderas para controlar el que las repeticiones continúen o finalicen.
“mientras” (while) es la estructura iterativa básica y lo que la caracteriza es que las acciones del cuerpo de la estructura se realizan siempre que la condición sea cierta, finalizando las repeticiones cuando la condición sea falsa. Además, siempre se pregunta por la condición antes de proceder a ejecutar el cuerpo de la estructura:
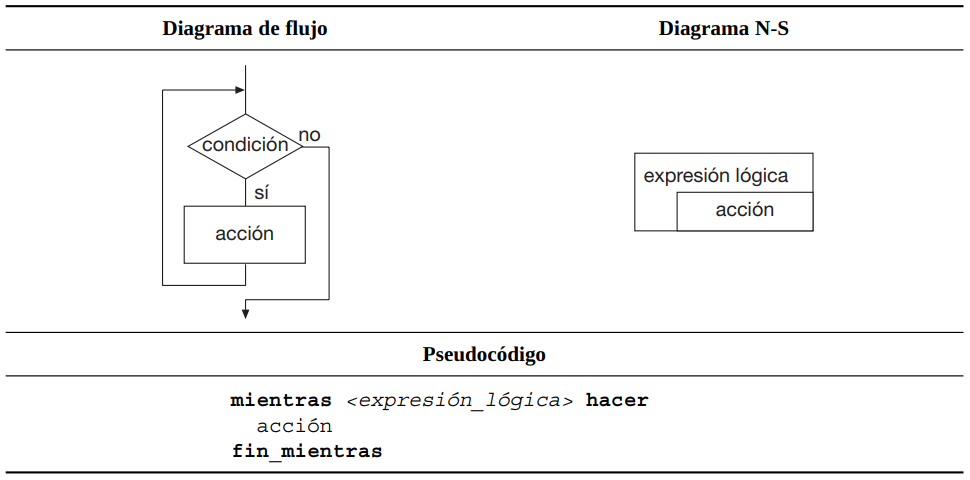
Usualmente se habla de más de una estructura iterativa, pero el Teorema de Böhm y Jacopini garantiza que todo algoritmo se puede escribir usando únicamente un tipo de estructura secuencial, un tipo de estructura selectiva y un tipo de estructura iterativa. Esto quiere decir que no se requiere más de un tipo de estructura iterativa y que siempre se puede reescribir el algoritmo para utilizar un solo tipo de estructura iterativa (lo que sea que se pueda hacer con los otros tipos de estructuras iterativas, también se puede hacer con un tipo de estructura iterativa seleccionado, por ejemplo usando únicamente la estructura iterativa “mientras”).
4.3.4 Anidamiento
Tanto las estructuras selectivas como las repetitivas pueden ir anidadas, unas en el interior de otras.
Una potencial estructura selectiva múltiple no es necesaria ya que sería equivalente a tener varias estructuras selectivas anidadas:
acciones_1
si_no
si condición_2 entonces
acciones_2
si_no
si condición_3 entonces
acciones_3
si_no
acciones_4
fin_si
fin_si
fin_si
Cuando se inserta una estructura iterativa dentro de otra, la estructura interna ha de estar totalmente incluida dentro de la externa:
acciones_1
mientras expresión_lógica_2 hacer
acciones_2
fin_mientras
acciones_3
fin_mientras
¿Si la expresión_lógica_1 es verdadera de manera consecutiva un número de veces n_1 y si la expresión_lógica_2 es verdadera de manera consecutiva un número de veces n_2 en cada ocasión que expresión_lógica_1 es verdadera, la acción o grupo de acciones del cuerpo de la estructura iterativa interna cuántas veces se ejecutará? ¿Si tengo una operación innecesaria en el cuerpo de dicha estructura, qué tanto se ve afectada la eficiencia del algoritmo? (¿qué tanto aumenta su costo computacional? ¿qué tanto aumenta su tiempo de ejecución?)
4.4 Ejemplos
Ejemplo 4.1 Realice el análisis y diseño en pseudocódigo de un algoritmo que obtenga e imprima el valor absoluto (|x|) de un número real (x) dado por el usuario mediante el uso del teclado.
Para cualquier número real x, el valor absoluto de x se denota por |x| y se define como:
|x| = \begin{cases} x & \text{Si } x \geq 0 \\ -x & \text{Si } x < 0 \end{cases}
var
real: x
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene e imprime por pantalla el valor absoluto de un número real dado por el usuario mediante el uso del teclado”)
escribir(“Por favor, ingrese un número real”)
leer(x)
si x < 0 entonces
x <- - x
fin_si
escribir(“El valor absoluto del número dado es” & x)
fin
Ejemplo 4.2 Realice el análisis y diseño en pseudocódigo de un algoritmo que obtenga e imprima el resultado de aplicar la función signo \big(\mathrm{sign}(x)\big) a un número real (x) dado por el usuario.
La función signo de un número real x, denotada por \mathrm{sgn}(x), \mathrm{sign}(x) o \mathrm{signo}(x), se puede definir de la siguiente manera:
\mathrm{sign}(x) = \begin{cases} 1 & \text{Si } x > 0 \\ 0 & \text{Si } x = 0 \\ -1 & \text{Si } x < 0 \end{cases}
var
real: x
entero: res
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene el valor de la función signo evaluada en un número real dado”)
escribir(“Por favor, ingrese un número real”)
leer(x)
si x > 0 entonces
res <- 1
si_no
si x < 0 entonces
res <- -1
si_no
res <- 0
fin_si
fin_si
escribir(“La función signo evaluada en” & x & ” es igual a ” & res)
fin
Ejemplo 4.3 Realice el análisis y diseño en pseudocódigo de un algoritmo que determine e imprima el mayor de dos números reales dados por el usuario. ¿Qué considera que debería hacer el algoritmo cuando los dos números dados son iguales? ¿hay una única alternativa o debo escoger entre varias posibles formas de atender esa situación?
Si los dos números reales dados por el usuario son diferentes, es poco y bastante sencillo lo que hay que hacer, casi totalmente obvio.
Por otro lado, hay varias maneras de manejar la situación cuando los dos números dados son iguales. Una de ellas es seguir pidiendo, tantas veces como sea necesario, un número distinto a los recibidos hasta el momento; otra opción podría ser pedir, tantas veces como sea necesario, dos nuevos números; o incluso otra opción podría ser imprimir que ninguno de los dos es mayor y no hacer nada más.
//En este algoritmo, si los dos números dados son iguales, entonces se pedirá
//tantas veces como sea necesario un número distinto a los recibidos
var
real: x, y
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo identifica el mayor de dos valores dados”)
escribir(“Por favor, ingrese un primer número real”)
leer(x)
escribir(“Por favor, ingrese un segundo número real, distinto al anterior”)
leer(y)
mientras x == y hacer
escribir(“Los números dados son iguales. Por favor, ingrese un número real, distinto a los dados previamente”)
leer(y)
fin_mientras
si x > y entonces
escribir(x & “es el mayor de los dos valores ingresados”)
si_no
escribir(y & “es el mayor de los dos valores ingresados”)
fin_si
fin
Ejemplo 4.4 Realice el análisis y diseño en pseudocódigo de un algoritmo que obtenga e imprima el factorial (k!) de un número entero no negativo (k \geq 0). ¿Qué considera que debería hacer el algoritmo si el número entero dado por el usuario es negativo?
El factorial de un número entero positivo k, denotado k! se puede definir como el producto de todos los números enteros positivos menores o iguales que k: k! = (2)(3) \cdots (k-2)(k-1)(k) o lo que es lo mismo, k! = (k)(k-1)(k-2) \cdots (3)(2)
Además, es necesario tener en cuenta que, 0! = 1 y es buena idea tener en cuenta que, 1! = 1 \qquad 2! = 2
Por otra parte, una forma en que el algoritmo puede atender la situación en la cual el usuario ingresa números enteros no negativos, es seguir pidiendo valores hasta que el usuario ingrese un número entero no negativo.
var
entero: k, res
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene el factorial de un número entero no negativo dado”)
escribir(“Por favor, ingrese un número entero no negativo”)
leer(k)
mientras k < 0 hacer
escribir(“Por favor, ingrese un número entero NO NEGATIVO”)
leer(k)
fin_mientras
si k < 2 entonces
res <- 1
si_no
res <- k
mientras k > 2 hacer
k <- k - 1
res <- res * k
fin_mientras
fin_si
escribir(“El factorial del número dado es” & res)
fin
Ejemplo 4.5 Realice el análisis y diseño en pseudocódigo de un algoritmo que determine e imprima si un número entero mayor que uno (k > 1) dado por el usuario es primo o no lo es.
En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1. Por el contrario, los números compuestos son los números naturales que tienen algún divisor natural aparte de sí mismos y del 1, y, por lo tanto, pueden factorizarse.
Adicionalmente, se sabe que:
- 2 y 3 son números primos
- 2 es el único número par que es primo.
- Un número impar solamente tiene divisores impares.
- Si un número (k) NO es divisible por un número natural (i) mayor o igual que dos y menor o igual que su raíz cuadrada (2 \leq i \leq \sqrt{k} \equiv 2^2 \leq i^2 \leq k) entonces es primo.
var
entero: k, i
booleano: seguirBusc
cadena: textoRes
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo determina si un número entero mayor que uno es primo o no lo es”)
escribir(“Por favor, ingrese un número entero mayor que uno”)
leer(k)
mientras k < 2 hacer
escribir(“Por favor, ingrese un número entero MAYOR QUE UNO”)
leer(k)
fin_mientras
//Se usará ” ” para los que son primos y ” NO ” para los que no
textoRes <- ” ”
si k > 3 entonces
si k % 2 == 0 entonces
escribir(“2 SI es divisor de” & k)
textoRes <- ” NO ”
si_no
escribir(“2 NO es divisor de” & k)
i <- 3
seguirBusc <- true
mientras seguirBusc hacer
si k % i == 0 entonces
escribir(i & ” SI es divisor de ” & k)
textoRes <- ” NO ”
seguirBusc <- false
si_no
escribir(i & ” NO es divisor de ” & k)
i <- i + 2
si i * i > k entonces
seguirBusc <- false
fin_si
fin_si
fin_mientras
fin_si
fin_si
escribir(“El número” & k & textoRes & “ES PRIMO”)
fin
Ejemplo 4.6 Realice el análisis y diseño en pseudocódigo de un algoritmo que obtenga e imprima una aproximación de la raíz cuadrada de un número real no negativo dado (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Los babilonios aproximaban raíces cuadradas haciendo cálculos mediante la media aritmética reiteradamente. En términos modernos, se trata de construir una sucesión a_{0}, a_{1}, a_{2}, a_{3}, \dots dada por: a_{n} = \frac{1}{2} \left( a_{n-1} + \frac{c}{a_{n-1}}\right) Puede demostrarse que esta sucesión matemática converge de manera que, a_{n} \xrightarrow[n \to \infty]{} \sqrt{c}
Nos damos cuenta que, \begin{aligned} a_n &= \frac{1}{2} \left(a_{n-1} + \frac{c}{a_{n-1}}\right) \\ &= \left(\frac{1}{2}\right) a_{n-1} + \frac{(c/2)}{a_{n-1}} \end{aligned} y como punto de partida o valor inicial podemos utilizar: \begin{aligned} a_1 &= \frac{1 + c}{2} \\ &= \left(\frac{1}{2}\right) + (c/2) \end{aligned}
var
entero: n
real: c, cMedios, a, aNew, eps
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene una aproximación de la raíz cuadrada de un número real no negativo dado (c). El algoritmo se detendrá cuando el cambio de una aproximación a la siguiente sea inferior a un número real positivo cercano a cero (epsilon)”)
escribir(“Por favor, ingrese un número real no negativo (c)”)
leer(c)
si c == 0 o c == 1 entonces
escribir(“La raíz cuadrada de” & c & ” es igual a ” & c)
si_no
escribir(“Por favor, ingrese un numero real positivo cercano a cero (epsilon)”)
leer(eps)
cMedios <- c / 2
n <- 2
a <- 0.5 + cMedios //Este es a_1
aNew <- 0.5 * a + cMedios / a
mientras a – aNew > eps hacer
n <- n + 1
a <- aNew
aNew <- 0.5 * a + cMedios / a
fin_mientras
escribir(“La raíz cuadrada de” & c & ” es aproximadamente igual a ” & aNew)
escribir(“(con el epsilon dado igual a” & eps & “, la aproximación corresponde al término” & n & ” de la sucesión)“)
fin_si
fin
Ejemplo 4.7 Realice el análisis y diseño en pseudocódigo de un algoritmo que calcule e imprima una aproximación de \cos(x),
\cos(x) = \sum\limits_{k = 0}^{\infty} \frac{(-1)^k}{(2k)!} x^{2k}
para un x dado por el usuario (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Se tiene que, \begin{aligned} S_n = \left[ \sum\limits_{k = 0}^{n} \left( \frac{(-1)^k}{(2k)!} x^{2k} \right) \right] \xrightarrow[n \to \infty]{} \cos(x) \end{aligned} de donde observamos que, \begin{aligned} S_n &= \left[ \sum\limits_{k = 0}^{n} \left( \frac{(-1)^k}{(2k)!} x^{2k} \right) \right] \\ &= \frac{1}{1} x^0 - \frac{1}{2} x^2 + \frac{1}{(4)(3)(2)} x^4 - \frac{1}{(6)(5)(4)(3)(2)} x^6 + \cdots \\ &= 1 - \frac{x^2}{2!} + \frac{\left(x^2\right)\left(x^2\right)}{(4)(3)(2!)} - \frac{\left(x^2\right)\left(x^4\right)}{(6)(5)(4!)} + \cdots \end{aligned} es decir, la magnitud de cada término cumple que, \begin{aligned} a_{i} &= \frac{x^i}{i!}, \text{ para } i = 2k = 0,2,4,\dots \\ &= \frac{x^2}{(i)(i-1)} \frac{x^{i-2}}{(i-2)!} \\ &= \frac{x^2}{(i)(i-1)} a_{i-2} \end{aligned} y estos términos se suman o restan de forma intercalada.
El algoritmo debe detenerse cuando: \begin{aligned} \big|S_{n} - S_{n-1}\big| &< \varepsilon \\ a_{i} &< \varepsilon \\ \end{aligned} En este caso el valor absoluto no es necesario debido a que a_i = \frac{x^i}{i!} para i = 2n siempre es positivo.
var
entero: i
real: x, xCuadrNegat, eps, term, res
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene una aproximación del coseno de un número real dado (x). El algoritmo se detendrá cuando el cambio de una aproximación a la siguiente sea inferior a un número real positivo cercano a cero (epsilon)”)
escribir(“Por favor, ingrese un número real no negativo (x)”)
leer(x)
res <- 1
si x != 0 entonces
escribir(“Por favor, ingrese un numero real positivo cercano a cero (epsilon)”)
leer(eps)
xCuadrNegat <- - x * x
i <- 2
term <- xCuadrNegat / i
res <- res + term
mientras term > eps o term < -eps hacer
i <- i + 2
term <- term * xCuadrNegat / (i * (i - 1))
res <- res + term
fin_mientras
fin_si
escribir(“El coseno de” & x & ” es igual a ” & res)
fin
var
entero: i
real: x, xCuadr, eps, magnTerm, res
booleano: restar
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene una aproximación del coseno de un número real dado (x). El algoritmo se detendrá cuando el cambio de una aproximación a la siguiente sea inferior a un número real positivo cercano a cero (epsilon)”)
escribir(“Por favor, ingrese un número real no negativo (x)”)
leer(x)
res <- 1
si x != 0 entonces
escribir(“Por favor, ingrese un numero real positivo cercano a cero (epsilon)”)
leer(eps)
xCuadr <- x * x
i <- 2
magnTerm <- xCuadr / i
restar <- true
res <- res - magnTerm
mientras magnTerm > eps hacer
i <- i + 2
magnTerm <- magnTerm * xCuadr / (i * (i - 1))
si restar entonces
restar <- false
res <- res + magnTerm
si_no
restar <- true
res <- res - magnTerm
fin_si
fin_mientras
fin_si
escribir(“El coseno de” & x & ” es igual a ” & res)
fin
¿Cuál es mejor, la opción 1 o la opción 2? ¿por qué?
Ejemplo 4.8 Realice el análisis y diseño en pseudocódigo de un algoritmo que obtenga e imprima una aproximación de una raíz de una función de los reales en los reales dada, usando el método de Newton-Raphson (teniendo en cuenta todas las consideraciones del método). Imagine que las funciones matemáticas se pueden declarar y leer como cualquier otro de los tipos de variables que ya hemos visto. Además, no olvide hacer todas las pruebas de escritorio que considere necesarias para garantizar que el diseño es eficaz y eficiente.
La serie de Taylor, alrededor de un punto x_{n-1}, de la función f(x) es, f(x) = f(x_{n-1}) + f'(x_{n-1}) (x - x_{n-1}) + \frac{f''(x_{n-1})}{2!} (x - x_{n-1})^2 + \cdots
Si utilizamos únicamente los dos primeros términos de la serie y asumimos que a partir de algún n, x_{n} va a estar muy cerca a una raíz de la función f(x) entonces, 0 \approx f\left(x_{n}\right) = f\left(x_{n-1}\right) + f'\left(x_{n-1}\right) \left(x_{n} - x_{n-1}\right) al despejar x_{n}, se tendría que, x_{n} = x_{n-1} - \frac{f\left(x_{n-1}\right)}{f'\left(x_{n-1}\right)} y x_{n} \xrightarrow[n \to \infty]{} x para un x tal que f(x) = 0.
Es así que al usuario se le debe pedir la función f, la función f', un valor inicial x_0, al menos un \varepsilon positivo cercano a cero para determinar cuando detenerse y un máximo al que se espera que nunca llegue n, pero que sirva de tope máximo de iteraciones para evitar que el algoritmo se quede infinitamente buscando una solución.
Además, el algoritmo debe deternerse cuando:
- \big|f'(x_n)\big| < \varepsilon_1, para evitar los efectos negativos de una división por cero o por un número muy cercano a cero.
- \big|f(x_n)\big| < \varepsilon_2, que es cuando se logra el objetivo deseado, una aproximación de una raíz de la función f.
- \big|x_{n} - x_{n-1}\big| < \varepsilon_3, que es cuando x_{n} es aproximadamente igual a x_{n-1}, lo que quiere decir que a partir de ese x_n será muy poco lo que se pueda avanzar en lograr el objetivo deseado.
//Nos imaginaremos que las funciones matemáticas se pueden declarar y leer
//como cualquier otro tipo de variable
var
función matemática de \mathbb{R} en \mathbb{R}: f, df
real: x0, x, xNew, eps, dfx, fx, delta
entero: maxIter, n
booleano: seguir
cadena: msg
inicio
escribir(“Bienvenido”)
escribir(“Método de Newton-Raphson para encontrar una raíz de un función”)
escribir(“Por favor, ingrese la función objetivo (f)”)
leer(f)
escribir(“Por favor, ingrese la derivada de la función objetivo (f’)”)
leer(df)
escribir(“Por favor, ingrese un numero real positivo menor que 0.01 (epsilon)”)
leer(eps)
escribir(“Por favor, ingrese un numero entero positivo (máximo de iteraciones)”)
leer(maxIter)
escribir(“Por favor, ingrese un numero real (x_0)”)
leer(x0)
xNew <- x0 //Para empezar el siguiente mientras con x0 = x = xNew
n <- 0
seguir <- true
mientras seguir == true y n < maxIter hacer
x <- xNew
dfx <- df(x)
si -eps < dfx y dfx < eps entonces
msg <- “La derivada evaluada en x_n se acerca demasiado a cero. df(x_n) =” & dfx
seguir <- false
si_no
fx <- f(x)
delta <- fx / dfx
xNew <- x – delta
n <- n + 1
si -eps < fx y fx < eps entonces
msg <- “Se encontró un x para el cual |f(x)| < epsilon. f(x_n) =” & fx
seguir <- false
si_no
si -eps < delta y delta < eps entonces
msg <- “No hubo un cambio superior a epsilon de x_n a x_{n+1}. x_n - x_{n+1} =” & delta
seguir <- false
fin_si
fin_si
fin_si
fin_mientras
si seguir == true entonces
msg <- “Se alcanzó el máximo de iteraciones:” & maxIter & “. x_0 =” & x0 & “. x_n =” & x & “. x_{n+1} =” & xNew
fin_si
escribir(msg)
escribir(“x_0 =” & x0)
escribir(“x_n =” & x)
escribir(“f’(x_{n+1}) =” & df(xNew))
escribir(“f(x_{n+1}) =” & f(xNew))
escribir(“x_{n+1} =” & xNew)
fin
4.5 Ejercicios
Parte A
Realice el análisis y diseño de cada algoritmo requerido, usando únicamente los elementos incluidos previamente en este material (por ejemplo, no use el operador ^ o ** para una potenciación, ya que ese elemento intencionalmente no fue incluido previamente):
Se convirtió en el Ejemplo 4.1.
Se convirtió en el Ejemplo 4.2.
Se convirtió en el Ejemplo 4.3.
Un algoritmo que le pida al usuario una temperatura y la escala de dicha temperatura, grados Centigrados o grados Fahrenheit, para calcular e imprimir la temperatura equivalente en la otra escala con respecto a la dada por el usuario (si recibe grados centigrados devolverá grados Fahrenheit y viceversa).
Un algoritmo que determine e imprima si la fecha del calendario gregoriano, asociada a un número de día, un número de mes y un número de año dados por el usuario, es una fecha válida o no.
Un algoritmo que imprima el número de día, de mes y de año correspondiente a la fecha del día siguiente, a partir de un número de día, número de mes y número de año dados por el usuario para una fecha válida del calendario gregoriano.
Se convirtió en el Ejemplo 4.5.
Un algoritmo que obtenga e imprima el máximo común divisor de dos números enteros dados por el usuario.
Un algoritmo que obtenga e imprima el mínimo común múltiplo de dos números enteros dados por el usuario.
Se convirtió en el Ejemplo 4.4.
Un algoritmo que obtenga e imprima la potencia k-ésima de un número real x, para k un número entero, con x y k dados por el usuario.
Se convirtió en el Ejemplo 4.6.
Un algoritmo que calcule e imprima una aproximación de \exp(x),
\exp(x) = \sum\limits_{k = 0}^{\infty} \frac{x^k}{k!}
para un x dado por el usuario (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Un algoritmo que calcule e imprima una aproximación de \ln(x),
\ln(x) = 2 \sum\limits_{k = 0}^{\infty} \left[ \frac{1}{2k+1}\left(\frac{x-1}{x+1}\right)^{2k+1} \right]
para un x>0 dado por el usuario (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Un algoritmo que calcule e imprima una aproximación de \sin(x),
\sin(x) = \sum\limits_{k= 0}^{\infty} \frac{(-1)^k}{(2k+1)!} x^{2k+1}
para un x dado por el usuario (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Se convirtió en el Ejemplo 4.7.
Un algoritmo que calcule e imprima una aproximación de \arcsin(x),
\arcsin(x) = \sum\limits_{k = 0}^{\infty} \frac{(2k)!}{4^k (k!)^2 (2k + 1)} x^{2k+1}
para un -1 < x < 1 dado por el usuario (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Calcule e imprima una aproximación para el número \pi, teniendo en cuenta que,
\frac{\pi}{4} = 4 \arctan \left(\frac{1}{5}\right) - \arctan \left(\frac{1}{239}\right)
y que
\arctan(x) = \sum\limits_{k = 0}^{\infty} \frac{(-1)^k}{2k+1} x^{2k+1}
(¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Un algoritmo que calcule e imprima una aproximación para el número áureo \varphi https://youtu.be/aopHcOm7a-w. Tenga en cuenta que,
\varphi = \lim_{n \to \infty} \frac{F_{n+1}}{F_n}
donde F_{n} denota el n-ésimo número de la serie de Fibonacci https://youtu.be/B6ztvqvZTsk (¿cuándo se consideraría que ya se llegó a una aproximación suficientemente buena? ¿en relación a ello, qué le pido al usuario como datos de entrada?).
Un algoritmo que reciba las notas de una cantidad no predeterminada de estudiantes de cierta asignatura (dejando de recibir notas en el momento en que se introduzca un valor de nota fuera del rango válido entre 0 y 5) y que imprima la cantidad de estudiantes que aprobaron la asignatura y la cantidad de estudiantes que la perdieron.
Un algoritmo que reciba las notas de una cantidad no predeterminada de estudiantes de cierta asignatura (dejando de recibir notas en el momento en que se introduzca un valor de nota fuera del rango válido entre 0 y 5) y que imprima el mínimo y el máximo de dichas notas.
Un algoritmo que reciba una cantidad no predeterminada de número reales, en donde se le debe preguntar al usuario si desea de dejar de ingresar valores antes de leer cada valor, y que en el momento en que el usuario informe que desea dejar de ingresar valores se impriman la media y la varianza (poblacionales) de los valores ingresados hasta ese momento (¿qué debe hacer mi algoritmo con las potenciales situaciones en donde el usuario ingresa un único valor o cuando no ingresa valor alguno?). Recuerde que:
\begin{aligned} \mu &= \frac{1}{N} \sum_{i = 1}^{N} x_i \\ \sigma^2 &= \frac{1}{N} \sum_{i = 1}^{N} \left(x_i - \mu\right)^2 = \left( \frac{1}{N} \sum_{i = 1}^{N} x_i^2 \right) - \mu^2 \end{aligned}
Parte B
Realice el análisis y diseño en pseudocódigo de cada algoritmo requerido, usando únicamente los elementos incluidos previamente en este material. Imagine que las funciones matemáticas se pueden declarar y leer como cualquier otro de los tipos de variables que ya hemos visto. Además, no olvide hacer todas las pruebas de escritorio que considere necesarias para garantizar que su diseño es eficaz y eficiente:
Un algoritmo que obtenga e imprima una aproximación de una raíz, entre dos números reales dados, de una función de los reales en los reales dada, usando el método de bisección (teniendo en cuenta todas las consideraciones del método).
Se convirtió en el Ejemplo 4.8.
Un algoritmo que obtenga e imprima una aproximación de la derivada (derivada numérica) evaluada en un número real dado, de una función de los reales en los reales dada (bien definida y derivable alrededor del número real dado).
Un algoritmo que obtenga e imprima una aproximación de la integral definida entre dos números reales dados, de una función de los reales en los reales dada (bien definida e integrable en el intervalo de integración), usando la regla del trapecio compuesta o regla de los trapecios.
Un algoritmo que obtenga e imprima una aproximación de la integral definida entre dos números reales dados, de una función de los reales en los reales dada (bien definida e integrable en el intervalo de integración), usando la regla o método de Simpson (1/3) compuesto.