# Solamente sirve para un parámetro vector con un solo elemento:
mi_fact_klength1_PIEP <- function(klength1){
if(length(klength1) == 1){
if(klength1 > 2){
res <- klength1
while(klength1 > 2){
klength1 <- klength1 - 1
res <- res * klength1
}
return(res)
}else{
if(klength1 >= 0){
return(ifelse(klength1 == 0, 1, klength1))
}
}
}
return(NaN)
}
# Factorial elemento a elemento de un vector dado:
mi_fact_PIEP <- function(k){
n <- length(k)
res <- NULL
for(i in 1:n){
res[i] = mi_fact_klength1_PIEP(k[i])
}
return(res)
}8 PIEP y POA en R
En esta sección se hará una revisión de los elementos básicos de programación imperativa estructurada procedimental (PIEP) y de programación orientada a arreglos (POA) de una implementación en R (obviamente, R como lenguaje de programación y NO como herramienta de cálculo o de análisis de datos).
En esta revisión se hace una pequeña introducción a R, a sus elementos básicos, a sus principales estructuras de control, a la creación de subprogramas, y al manejo de sus tipos de datos compuestos.
Se espera que al finalizar las actividades de esta sección, el estudiante entienda y tenga clara la manera en que un algoritmo, diseñado bajo los paradigmas de programación imperativa estructurada procedimental y orientado a arreglos, se puede implementar mediante el uso del lenguaje de programación R.
- Para la siguiente sección, lea todo y ejecute todo el código que allí se incluye, haciendo todas las pruebas, cambios y experimentos que se les puedan ocurrir sobre dicho código.
En sus propias palabras, explique lo que le transmitió y lo que le enseño cada parte de lo que leyó, ejecutó, probó y experimentó; incluya su discusión, reflexiones y conclusiones al respecto; exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para poder compartirlas en clase.
8.1 Elementos básicos de PIEP y POA en R
Cuaderno computacional en Google Colaboratory:
Elementos básicos, estructuras de control, creación de subprogramas y tipos de datos compuestos en R
8.2 Ejemplos
Ejemplo 8.1 Haga un adecuado análisis, diseño e implementación en R de un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número entero y que devuelvan el factorial del número recibido. Implemente una prueba rápida (una serie de instrucciones) que le permita probar los subprogramas requeridos para varios valores distintos. Por último, implemente una serie de instrucciones que permita realiar una comparación de tiempos entre las dos soluciones solicitadas y la función factorial() de R.
El factorial de un número entero positivo k, denotado k! se puede definir como el producto de todos los números enteros positivos menores o iguales que k: k! = (2)(3) \cdots (k-2)(k-1)(k) o lo que es lo mismo, k! = (k)(k-1)(k-2) \cdots (3)(2)
Además, es necesario tener en cuenta que, 0! = 1 y es buena idea tener en cuenta que, 1! = 1 \qquad 2! = 2
# Solamente sirve para un parámetro vector con un solo elemento:
mi_fact_klength1_POA <- function(klength1){
if(length(klength1)==1){
if(klength1 > 2){
return(prod(2:klength1))
}else{
if(klength1 >= 0){
return(ifelse(klength1 == 0, 1, klength1))
}
}
}
return(NaN)
}
# `Vectorize()` toma una función y devuelve una función capaz de devolver
# el mismo resultado pero elemento a elemento de un vector dado:
mi_fact_POA_Vectorize <- Vectorize(mi_fact_klength1_POA)
# Implementación propia (con la ayuda de `sapply()`) capaz de devolver el
# factorial elemento a elemento de un vector dado:
mi_fact_POA_sapply <- function(k){
sapply(k, mi_fact_klength1_POA)
}v <- c(-14, -8, 0, 1, 2, 8, 14)
for(i in v){
cat("(", sprintf(i, fmt='%3.0f'), ")!\t",
sprintf(mi_fact_klength1_PIEP(i), fmt='%12.0f'), "\t",
sprintf(mi_fact_klength1_POA(i), fmt='%12.0f'), "\t",
sprintf(factorial(i), fmt='%12.0f'), "\n", sep = "")
}(-14)! NaN NaN NaN( -8)! NaN NaN NaN
( 0)! 1 1 1
( 1)! 1 1 1
( 2)! 2 2 2
( 8)! 40320 40320 40320
( 14)! 87178291200 87178291200 87178291200v <- c(-14, -8, 0, 1, 2, 8, 14)
resul <- c(mi_fact_PIEP(v), mi_fact_POA_Vectorize(v),
mi_fact_POA_sapply(v), factorial(v))
resul <- matrix(resul, ncol = 4)
colnames(resul) <- c("mi_fact_PIEP(v)", "mi_fact_POA_Vectorize(v)",
"mi_fact_POA_sapply(v)", "factorial(v)")
rownames(resul) <- paste0("(", v, ")!")
resul mi_fact_PIEP(v) mi_fact_POA_Vectorize(v) mi_fact_POA_sapply(v)
(-14)! NaN NaN NaN
(-8)! NaN NaN NaN
(0)! 1 1 1
(1)! 1 1 1
(2)! 2 2 2
(8)! 40320 40320 40320
(14)! 87178291200 87178291200 87178291200
factorial(v)
(-14)! NaN
(-8)! NaN
(0)! 1
(1)! 1
(2)! 2
(8)! 40320
(14)! 87178291200# `require()` intenta cargar la librería, si no la puede cargar devuelve FALSE
if (!require(microbenchmark)){
install.packages("microbenchmark") # Instala librería
library(microbenchmark) # Carga librería
}Loading required package: microbenchmarkWarning: package 'microbenchmark' was built under R version 4.3.3k = 13mbm <- microbenchmark("mi_fact_klen1_PIEP"={mi_fact_klength1_PIEP(k)},
"mi_fact_klen1_POA"={mi_fact_klength1_POA(k)},
"mi_fact_PIEP"={mi_fact_PIEP(k)},
"mi_fact_POA_Vectorize"={mi_fact_POA_Vectorize(k)},
"mi_fact_POA_sapply"={mi_fact_POA_sapply(k)},
"factorial"={factorial(k)},
times=1e3)
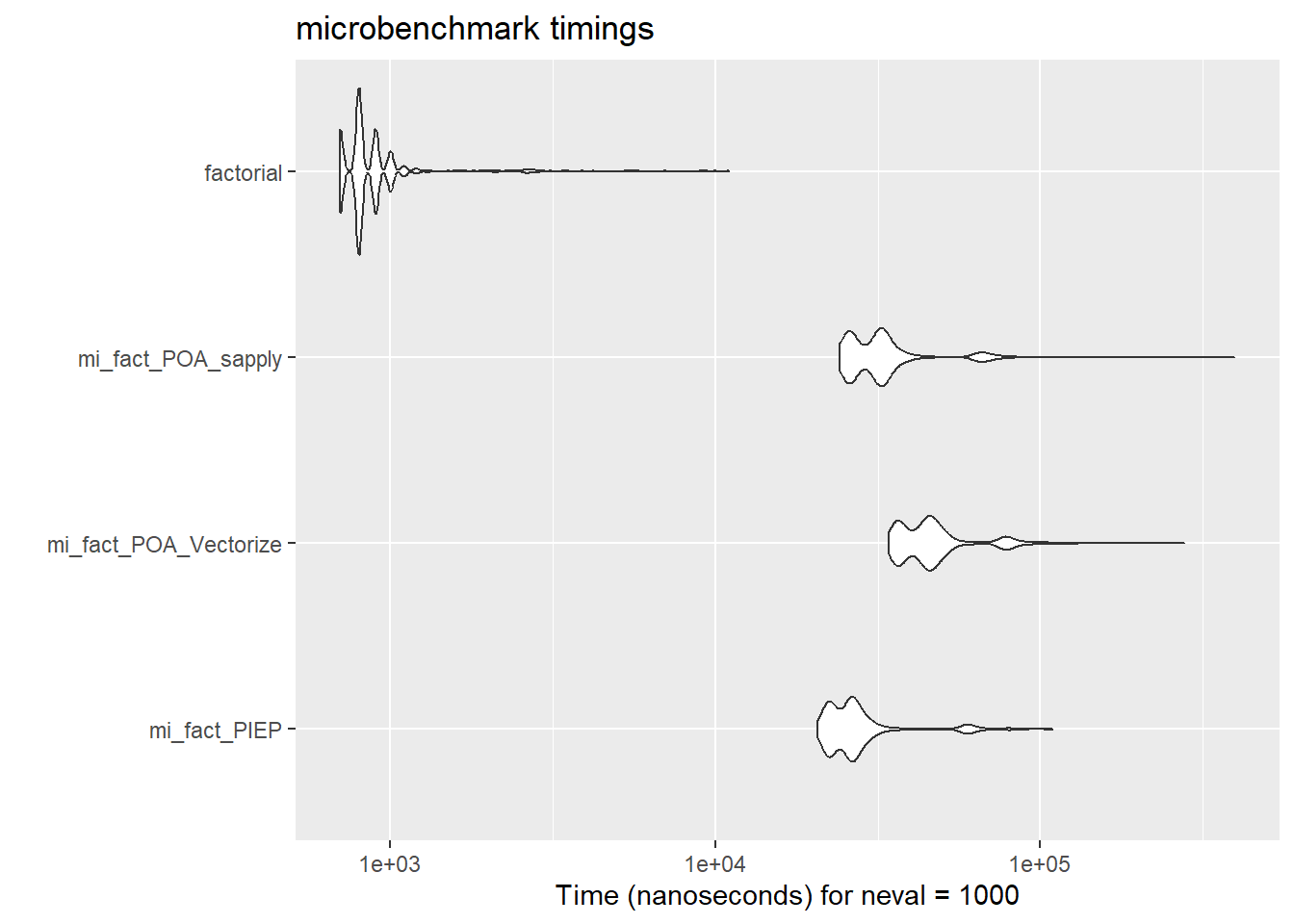
mbm # TablaUnit: nanoseconds
expr min lq mean median uq max neval cld
mi_fact_klen1_PIEP 500 600 670.9 600 700 12100 1000 a
mi_fact_klen1_POA 300 400 494.9 500 500 23600 1000 a
mi_fact_PIEP 1100 1200 1358.4 1300 1400 14300 1000 a
mi_fact_POA_Vectorize 14800 15300 16105.1 15500 15900 76500 1000 b
mi_fact_POA_sapply 6500 6800 7940.2 6900 7000 748000 1000 c
factorial 100 200 235.0 200 300 4700 1000 a boxplot(mbm, bty="n") # Gráfico boxplot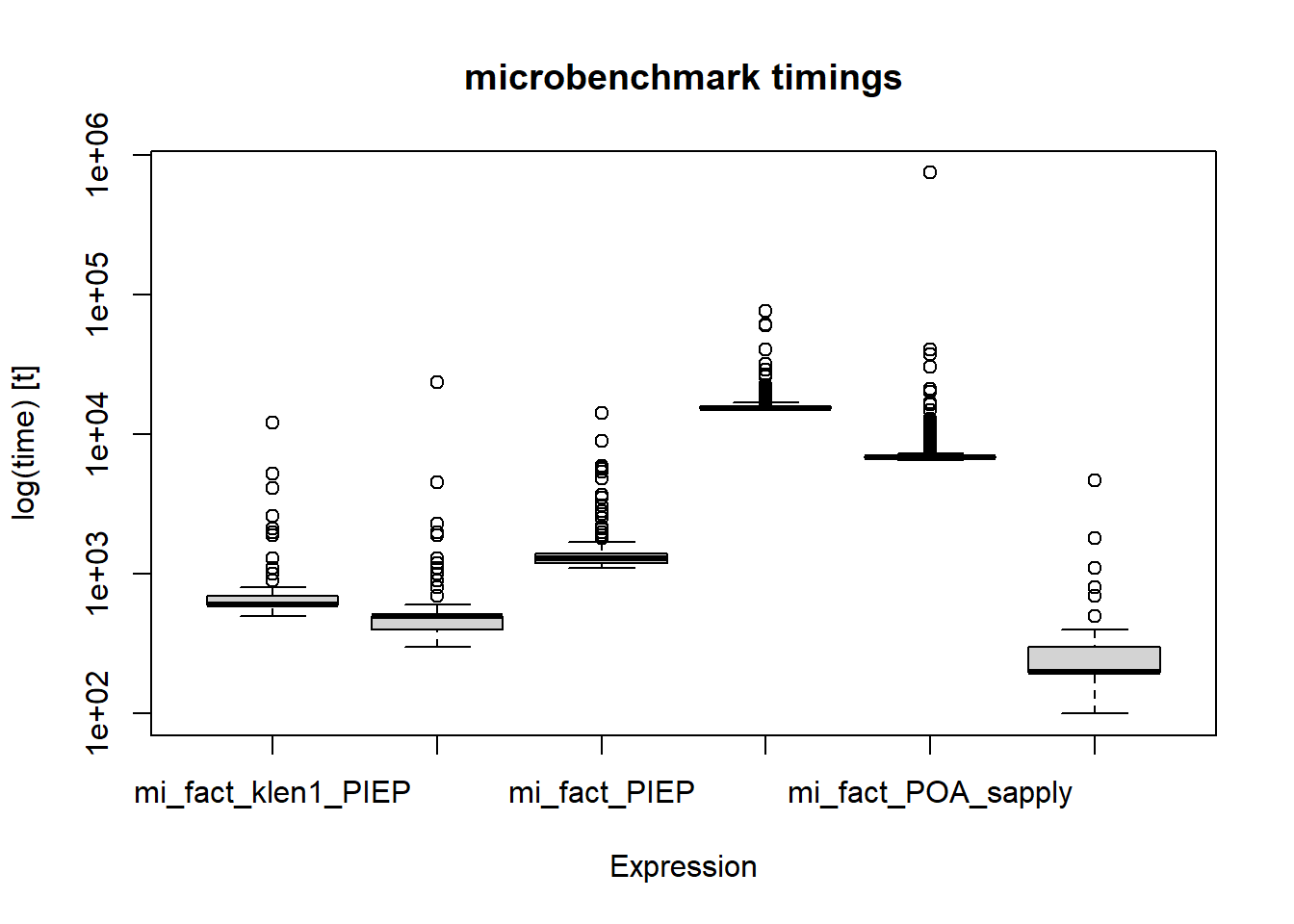
if (!require(ggplot2)){
install.packages("ggplot2")
library(ggplot2)
}Loading required package: ggplot2autoplot(mbm) # gráfico parecido al boxplot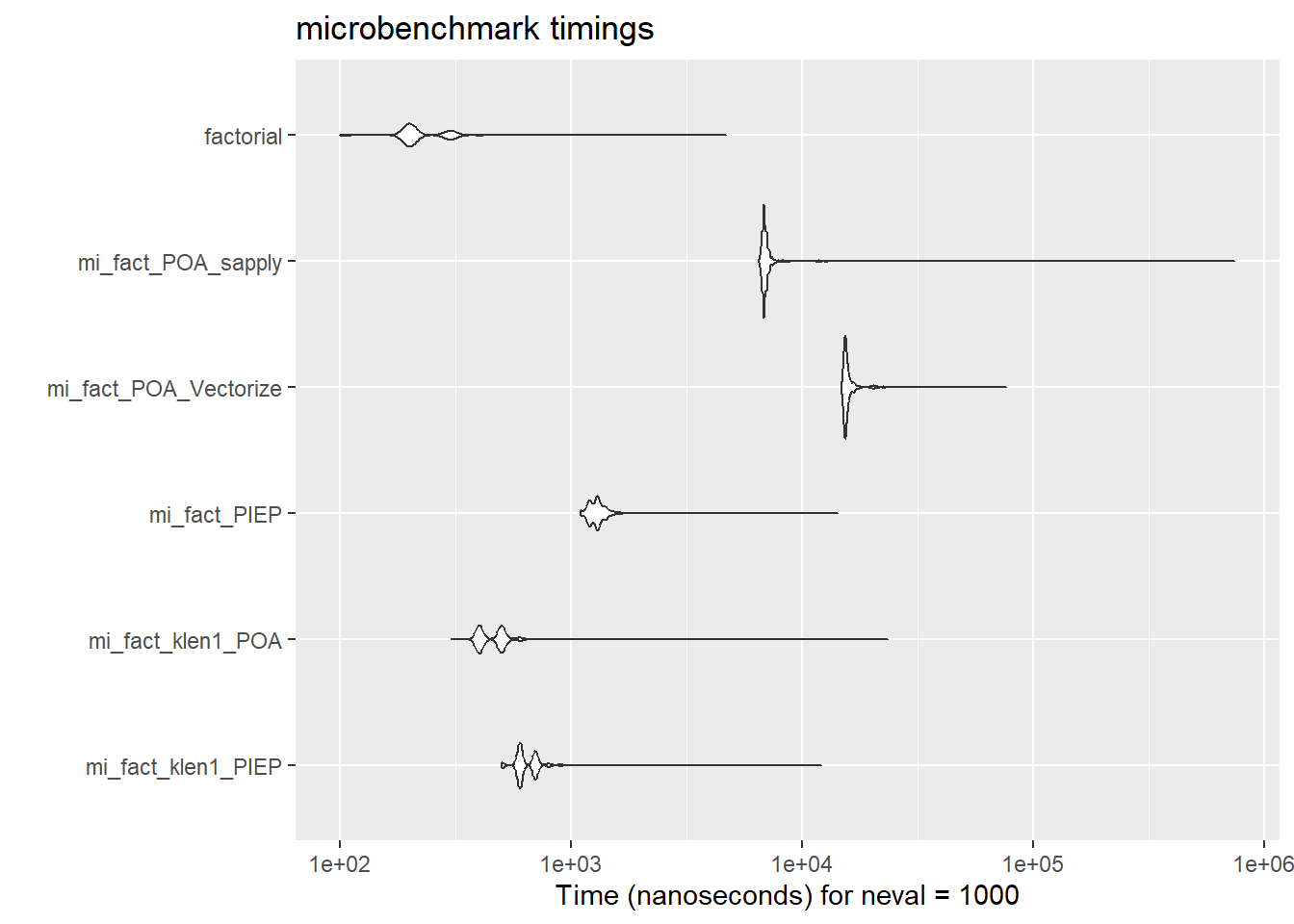
# `require()` intenta cargar la librería, si no la puede cargar devuelve FALSE
if (!require(microbenchmark)){
install.packages("microbenchmark") # Instala librería
library(microbenchmark) # Carga librería
}
set.seed(10310506)
k <- sample(0:15, 25, replace=TRUE)
print(k) [1] 5 0 6 14 15 7 10 13 6 4 15 13 4 2 15 13 13 5 12 8 7 2 2 9 1mbm <- microbenchmark("mi_fact_PIEP"={mi_fact_PIEP(k)},
"mi_fact_POA_Vectorize"={mi_fact_POA_Vectorize(k)},
"mi_fact_POA_sapply"={mi_fact_POA_sapply(k)},
"factorial"={factorial(k)},
times=1e3)
mbm # TablaUnit: nanoseconds
expr min lq mean median uq max neval cld
mi_fact_PIEP 20700 22900 28831.1 25900 28100 109000 1000 a
mi_fact_POA_Vectorize 34200 37800 49271.4 44900 49400 277600 1000 b
mi_fact_POA_sapply 24100 26400 34549.3 31400 33800 397300 1000 c
factorial 700 800 967.9 800 900 11000 1000 dEjemplo 8.2 Haga un adecuado análisis, diseño e implementación en R de un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan una aproximación de la función coseno evaluada en un número real dado entre 0 y \frac{\pi}{4}. Los subprogramas solicitados deben tener en cuenta que:
- \sum\limits_{k = 0}^{n} \frac{(-1)^k}{(2k)!} c^{2k} \xrightarrow[n \to \infty]{} \cos(c)
- En esta ocasión, fije la cantidad de términos a usar de la serie. Es decir, primero analice y determine, a lo sumo, cuántos términos son mayores que 1 \times 10^{-15} para c entre 0 y \frac{\pi}{4}, y luego en la implementación use siempre esa misma cantidad de términos.
Adicionalmente, implemente una prueba rápida (una serie de instrucciones) que le permita probar los subprogramas requeridos para varios valores distintos. Por último, implemente una serie de instrucciones que permita realizar una comparación de tiempos entre las dos soluciones solicitadas y la función cos() de R.
Para c entre 0 y \frac{\pi}{4}, \frac{1}{(2k)!} c^{2k} < \frac{1}{(2k)!} \left(\frac{\pi}{4}\right)^{2k} o sea que si se encuentra k_0 tal que para todo k > k_0 se tiene que, \frac{1}{(2k)!} \left(\frac{\pi}{4}\right)^{2k} < 1 \times 10^{-15} entonces \frac{1}{(2k)!} c^{2k} < 1 \times 10^{-15} para todo k > k_0 y para todo c entre 0 y \frac{\pi}{4}.
Reescribiendo,
\begin{align*} \frac{1}{(2k)!} \left(\frac{\pi}{4}\right)^{2k} &< 1 \times 10^{-15} \\ \left(\frac{\pi}{4}\right)^{2k} &< \frac{(2k)!}{1 \times 10^{15}} \\ \left(\frac{\pi}{4}\right)^{2k} - \frac{(2k)!}{1 \times 10^{15}} &< 0 \end{align*}
Encontrando numéricamente una raíz para la función f(k) = \left(\frac{\pi}{4}\right)^{2k} - \frac{(2k)!}{1 \times 10^{15}}, concluimos que \frac{1}{(2k)!} \left(\frac{\pi}{4}\right)^{2k} < 1 \times 10^{-15} para todo k > 8.000312.
Es decir, para un c entre 0 y \frac{\pi}{4}, los términos k = 0, 1, \dots, 8 de la serie serán los únicos que podrían llegar a ser mayores que 1 \times 10^{-15}. En otras palabras, los términos k = 0, 1, \dots, 8 serán más que suficientes para cualquier c entre 0 y \frac{\pi}{4}, ya que, para todo c entre 0 y \frac{\pi}{4}, los términos k = 9 en adelante serán menores que 1 \times 10^{-15}.
# Unicamente para $0 \leq c \leq \frac{\pi}{4}$
mi_cos_serie_clen1_PIEP <- function(clen1){
res <- 1.0
if(clen1 != 0){
cCuadr <- clen1 * clen1
magnTerm <- cCuadr / 2
restar <- TRUE
res <- res - magnTerm
iMax <- 16
for(i in seq(4, iMax, 2)){
magnTerm <- magnTerm * cCuadr / (i * (i - 1))
if(restar){
restar <- FALSE
res <- res + magnTerm
}
else{
restar <- TRUE
res <- res - magnTerm
}
}
}
res
}
mi_cos_serie_PIEP <- function(c){
len <- length(c)
res <- NULL
for(i in 1:len){
res[i] = mi_cos_serie_clen1_PIEP(c[i])
}
res
}# Solamente sirve para un parámetro vector con un solo elemento:
mi_cos_serie_clen1_POA <- function(clen1){
kMax <- 8
iMax <- 16
res <- 1
if(clen1 != 0){
num <- cumprod(rep(-clen1*clen1, kMax)) # -x^2, x^4, -x^6, ..., -x^{14}, x^{16}
den <- cumprod(2:iMax)[c(TRUE, FALSE)] # 2!, 4!, 6!, ..., 16!
res = res + sum(num/den)
}
res
}
# `Vectorize()` toma una función y devuelve una función capaz de devolver
# el mismo resultado pero elemento a elemento de un vector dado:
mi_cos_serie_POA_Vectorize <- Vectorize(mi_cos_serie_clen1_POA)
# Implementación propia (con la ayuda de `sapply()`) capaz de devolver el
# coseno elemento a elemento de un vector dado:
mi_cos_serie_POA_sapply <- function(c){
sapply(c, mi_cos_serie_clen1_POA)
}
# Implementación propia capaz de devolver el
# coseno elemento a elemento de un vector dado:
mi_cos_serie_POA <- function(c){
kMax <- 8
iMax <- 16
indx <- c != 0
c <- c[indx]
len <- length(c)
num <- matrix(rep(-c*c, kMax), len)
num <- apply(num, 1, cumprod)
den <- cumprod(2:iMax)[c(TRUE, FALSE)]
res <- NULL
res[indx] <- 1 + (1/den) %*% num
res[!indx] <- 1
res
}v <- seq(0, pi/4, length=7)
for(i in v){
cat("cos(", sprintf(i, fmt='%18.16f'), ")\t",
sprintf(mi_cos_serie_clen1_PIEP(i), fmt='%20.16f'), "\t",
sprintf(mi_cos_serie_clen1_POA(i), fmt='%20.16f'), "\t",
sprintf(cos(i), fmt='%20.16f'), "\n", sep = "")
}cos(0.0000000000000000) 1.0000000000000000 1.0000000000000000 1.0000000000000000
cos(0.1308996938995747) 0.9914448613738104 0.9914448613738104 0.9914448613738104
cos(0.2617993877991494) 0.9659258262890684 0.9659258262890683 0.9659258262890683
cos(0.3926990816987241) 0.9238795325112867 0.9238795325112867 0.9238795325112867
cos(0.5235987755982988) 0.8660254037844386 0.8660254037844387 0.8660254037844387
cos(0.6544984694978735) 0.7933533402912352 0.7933533402912352 0.7933533402912353
cos(0.7853981633974483) 0.7071067811865475 0.7071067811865475 0.7071067811865476v <- seq(0, pi/4, length=7)
resul <- c(mi_cos_serie_PIEP(v), mi_cos_serie_POA_Vectorize(v),
mi_cos_serie_POA_sapply(v), mi_cos_serie_POA(v), cos(v))
resul <- matrix(resul, ncol = 5)
colnames(resul) <- c("mi_cos_serie_PIEP(v)", "mi_cos_serie_POA_Vectorize(v)",
"mi_cos_serie_POA_sapply(v)", "mi_cos_serie_POA(v)", "cos(v)")
rownames(resul) <- paste0("cos(", v, ")")
resul mi_cos_serie_PIEP(v) mi_cos_serie_POA_Vectorize(v)
cos(0) 1.0000000 1.0000000
cos(0.130899693899575) 0.9914449 0.9914449
cos(0.261799387799149) 0.9659258 0.9659258
cos(0.392699081698724) 0.9238795 0.9238795
cos(0.523598775598299) 0.8660254 0.8660254
cos(0.654498469497873) 0.7933533 0.7933533
cos(0.785398163397448) 0.7071068 0.7071068
mi_cos_serie_POA_sapply(v) mi_cos_serie_POA(v) cos(v)
cos(0) 1.0000000 1.0000000 1.0000000
cos(0.130899693899575) 0.9914449 0.9914449 0.9914449
cos(0.261799387799149) 0.9659258 0.9659258 0.9659258
cos(0.392699081698724) 0.9238795 0.9238795 0.9238795
cos(0.523598775598299) 0.8660254 0.8660254 0.8660254
cos(0.654498469497873) 0.7933533 0.7933533 0.7933533
cos(0.785398163397448) 0.7071068 0.7071068 0.7071068# `require()` intenta cargar la librería, si no la puede cargar devuelve FALSE
if (!require(microbenchmark)){
install.packages("microbenchmark") # Instala librería
library(microbenchmark) # Carga librería
}
set.seed(11081348)
c <- runif(1, 0, pi/4)
cat("c =", c)c = 0.06901471mbm <- microbenchmark("mi_cos_clen1_PIEP"={mi_cos_serie_clen1_PIEP(c)},
"mi_cos_clen1_POA"={mi_cos_serie_clen1_POA(c)},
"mi_cos_PIEP"={mi_cos_serie_PIEP(c)},
"mi_cos_serie_POA_Vectorize"={mi_cos_serie_POA_Vectorize(c)},
"mi_cos_serie_POA_sapply"={mi_cos_serie_POA_sapply(c)},
"mi_cos_serie_POA"={mi_cos_serie_POA(c)},
"cos"={cos(c)},
times=1e3)
mbm # TablaUnit: nanoseconds
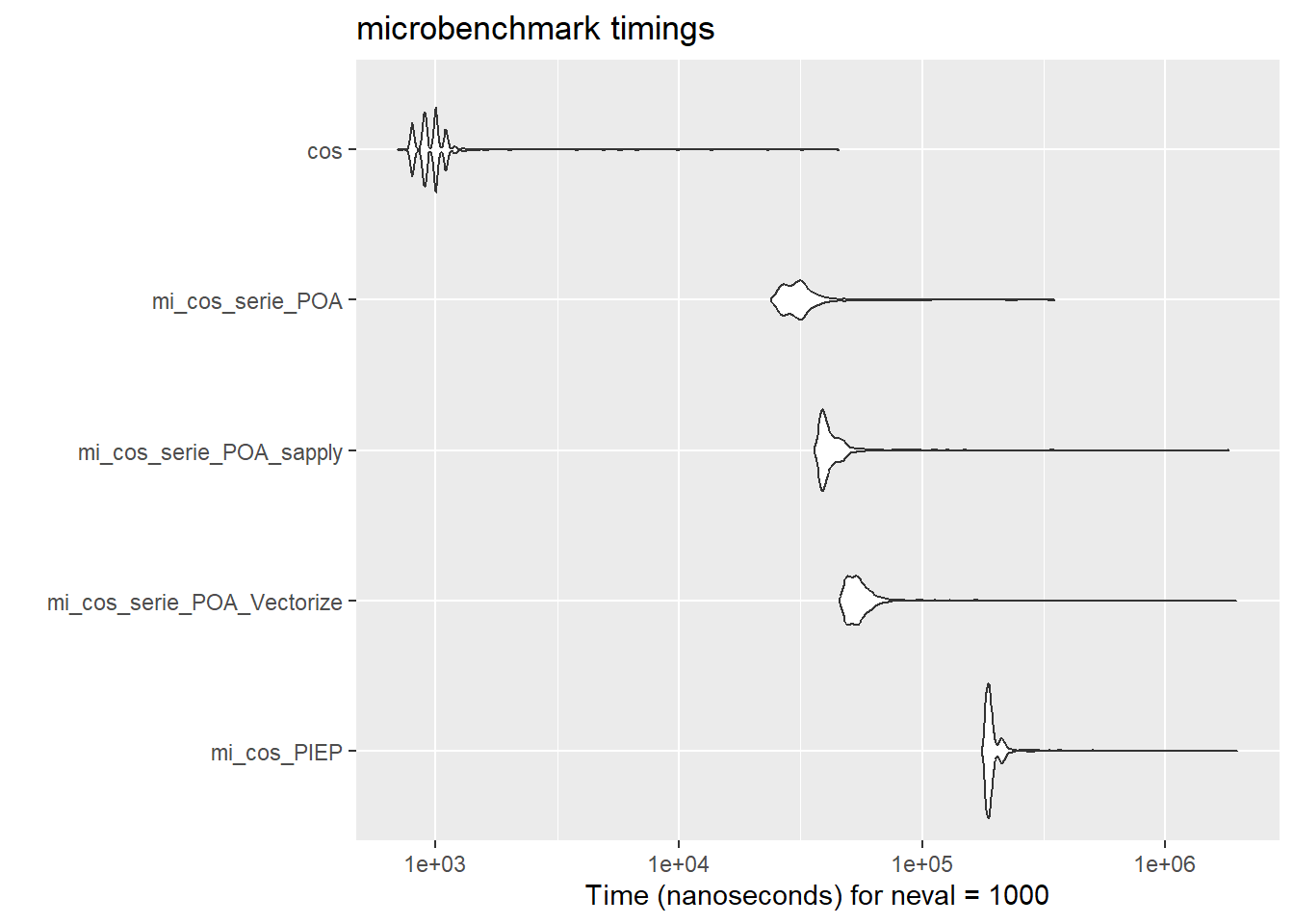
expr min lq mean median uq max neval cld
mi_cos_clen1_PIEP 8600 9200 10632.9 9700 10500 296100 1000 a
mi_cos_clen1_POA 1200 1400 1721.7 1500 1700 37900 1000 b
mi_cos_PIEP 9200 10100 11278.1 10700 11600 193900 1000 a
mi_cos_serie_POA_Vectorize 16600 18200 20299.3 19100 20700 165700 1000 c
mi_cos_serie_POA_sapply 7800 8400 9942.9 8900 9500 718800 1000 a
mi_cos_serie_POA 13100 15000 16976.1 16100 17400 144300 1000 d
cos 100 100 200.3 200 200 5000 1000 eif (!require(ggplot2)){
install.packages("ggplot2")
library(ggplot2)
}
autoplot(mbm) # gráfico parecido al boxplot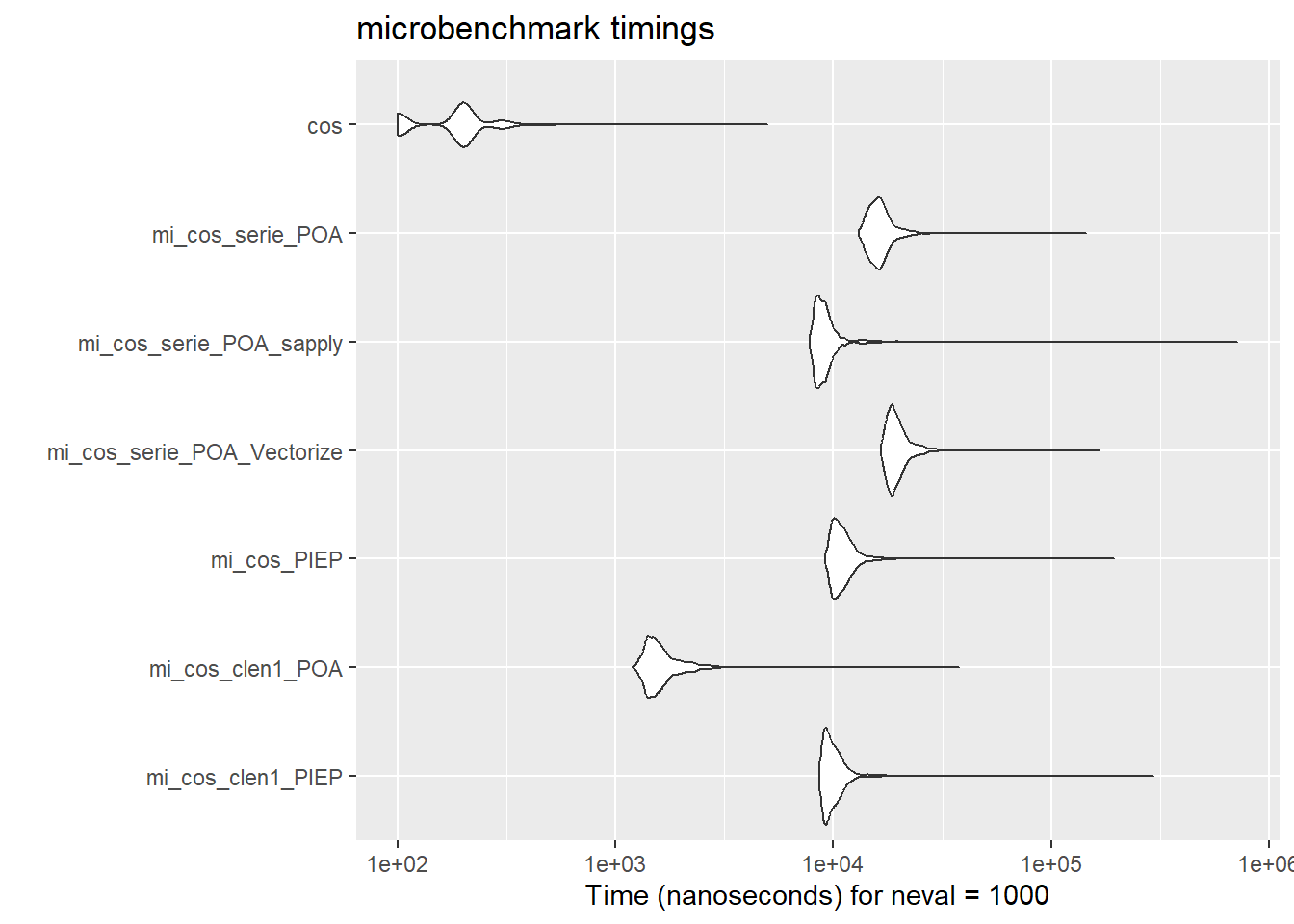
# `require()` intenta cargar la librería, si no la puede cargar devuelve FALSE
if (!require(microbenchmark)){
install.packages("microbenchmark") # Instala librería
library(microbenchmark) # Carga librería
}
set.seed(11081348)
c <- runif(20, 0, pi/4)
print(c) [1] 0.06901471 0.10078974 0.11829167 0.60410898 0.17810267 0.08819629
[7] 0.46757247 0.42381621 0.45641103 0.74174346 0.75628327 0.74122467
[13] 0.55322552 0.47472847 0.37166666 0.32539549 0.01587700 0.48829730
[19] 0.15890795 0.58516338mbm <- microbenchmark("mi_cos_PIEP"={mi_cos_serie_PIEP(c)},
"mi_cos_serie_POA_Vectorize"={mi_cos_serie_POA_Vectorize(c)},
"mi_cos_serie_POA_sapply"={mi_cos_serie_POA_sapply(c)},
"mi_cos_serie_POA"={mi_cos_serie_POA(c)},
"cos"={cos(c)},
times=1e3)
mbm # TablaUnit: nanoseconds
expr min lq mean median uq max neval
mi_cos_PIEP 175700 184600 198241.1 188950 195650 1977100 1000
mi_cos_serie_POA_Vectorize 45700 50000 57574.7 53600 57700 1956500 1000
mi_cos_serie_POA_sapply 36200 38700 44643.7 40200 44200 1823800 1000
mi_cos_serie_POA 24000 27550 32344.2 30700 33250 348100 1000
cos 700 900 1100.4 1000 1000 45300 1000
cld
a
b
c
d
e8.3 Ejercicios
- En las soluciones de PIEP, NO debe haber llamados recursivos de una o más funciones que puedan ser reemplazados por el uso de estructuras iterativas.
- En las soluciones de POA (array-oriented), NO debe haber uso de estructuras iterativas que puedan ser reemplazadas por el uso de operaciones o funciones básicas de tipos de datos compuestos.
- Para los subprogramas solicitados pueden usar todos los operadores y las funciones que se referencian en Elementos básicos, estructuras de control, creación de subprogramas y tipos de datos compuestos en R (intencionalmente, el operador
^no fue referenciado), todos los demás operadores y funciones de R los pueden usar para la parte de prueba y comparación de resultados.
Haga un adecuado ANÁLISIS, DISEÑO e IMPLEMENTACIÓN EN R de:
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y un número entero (k), y que devuelvan la potencia con exponente entero c^k.
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y un vector de números reales asociados a los coeficientes de un polinomio en orden ascendiente \big(a_0 =\big.
v[1], a_1 =v[2], \dots, a_{n-1} =v[n]y \big.p(x) = a_0 + a_1 x + \cdots + a_{n-1} x^{n-1}\big), y que devuelvan el polinomio evaluado en el número real recibido \big(p(c)\big).-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban dos números enteros no negativos \left(k\right. y \left.r \leq k\right), y que devuelvan la cantidad de reordenamientos posibles de r elementos que no se repiten tomados de un conjunto de k elementos (número de permutaciones o variaciones sin repetición, por ejemplo ver: Combinatoria - Wikipedia). Los subprogramas solicitados deben tener en cuenta que:
- El número de permutaciones sin elementos repetidos es P(k, r) = k P r = \frac{k!}{(k-r)!}
- La solución debe computacionalmente mejor, es decir, debe tener un número total de operaciones menor, que simplemente hacer
Factorial(k) / Factorial(k-r)para una funciónFactorial()que devuelva el factorial de un número entero no negativo.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciba dos números enteros no negativos \left(k\right. y \left.r \leq k\right), y que devuelvan la cantidad de subconjuntos posibles de r elementos tomados de un conjunto de k elementos (número de combinaciones sin repetición, por ejemplo ver: Combinatoria - Wikipedia). Los subprogramas solicitados deben tener en cuenta que:
- El número de combinaciones (coeficiente binomial) es C(k, r) = k C r = \binom{k}{r} = \frac{k!}{r! (k-r)!}
- La solución debe ser computacionalmente mejor, es decir, debe tener un número total de operaciones menor, que simplemente hacer
Factorial(k) / ( Factorial(r) * Factorial(k-r) )oPermutacion(k,r) / Factorial(r)para una funciónFactorial()que devuelva el factorial de un número entero no negativo y una funciónPermutacion(,)que devuelva el número de permutaciones.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y que devuelvan una aproximación del seno de c \big(\sin(c)\big). Los subprogramas solicitados deben tener en cuenta que:
- Si c < 0, entonces \sin(c) = -\sin(-c), lo que reduce el problema a calcular el seno de un valor mayor que cero (0).
- Si c \geq 2 \pi, entonces \sin(c) = \sin(c - k \, 2 \pi), lo que reduce el problema a calcular el seno de un valor entre 0 y 2 \pi.
- Si \pi \leq c < 2 \pi, entonces \sin(c) = -\sin(c - \pi), lo que reduce el problema a calcular el seno de un valor entre 0 y \pi.
- Si \frac{\pi}{2} \leq c < \pi, entonces \sin(c) = \sin(\pi - c), lo que reduce el problema a calcular el seno de un valor entre 0 y \frac{\pi}{2}.
- Si \frac{\pi}{4} \leq c < \frac{\pi}{2}, entonces \sin(c) = \cos\left(\frac{\pi}{2} - c\right), lo que reduce el problema a calcular el coseno de un valor entre 0 y \frac{\pi}{4}.
- \sum\limits_{k = 0}^{n} \frac{(-1)^k}{(2k+1)!} c^{2k+1} \xrightarrow[n \to \infty]{} \sin(c), que se debe utilizar unicamente para calcular el seno de un valor entre 0 y \frac{\pi}{4}.
- En esta ocasión, fije la cantidad de términos a usar de la serie. Es decir, primero analice y determine, a lo sumo, cuántos términos son mayores que 1 \times 10^{-15} para c entre 0 y \frac{\pi}{4}, y luego en la implementación use siempre esa misma cantidad de términos.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y que devuelvan una aproximación del arco tangente de c \big(\arctan(c)\big). Puede tomar \sqrt{3} \approx 1.7320508075688773. El subprograma solicitado debe tener en cuenta que:
- Si c < 0, entonces \arctan(c) = - \arctan(-c), lo que reduce el problema a calcular el arco tangente de un valor mayor que cero.
- Si c > 1, entonces \arctan(c) = \frac{\pi}{2} - \arctan\left(\frac{1}{c}\right), lo que reduce el problema a calcular el arco tangente de un valor menor o igual que uno.
- Si c > 2 - \sqrt{3}, entonces \arctan(c) = \frac{\pi}{6} + \arctan \left( \frac{\sqrt{3} \, c - 1}{\sqrt{3} + c} \right), lo que reduce el problema a calcular el arco tangente de un valor menor o igual que 2 - \sqrt{3}.
- \sum_{k = 0}^{n} \frac{(-1)^k}{2k+1} c^{2k+1} \xrightarrow[n \to \infty]{} \arctan(c), que se debe utilizar unicamente para calcular el arco tangente de un valor entre 0 y 2 - \sqrt{3}.
- En esta ocasión, fije la cantidad de términos a usar de la serie. Es decir, primero analice y determine, a lo sumo, cuántos términos son mayores que 1 \times 10^{-15} para c entre 0 y 2 - \sqrt{3}, y luego en la implementación use siempre esa misma cantidad de términos.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y que devuelvan una aproximación de la función exponencial evaluada en c \big(\exp(c)\big). Puede tomar \mathrm{e} \approx 2.7182818284590452. El subprograma solicitado debe tener en cuenta que:
- Si c < 0, entonces \exp(c) = \frac{1}{\exp(-c)} lo que reduce el problema a calcular la función exponencial de un valor mayor que cero.
- Si c > 1, entonces, \exp(c) = \exp(k + d) = \exp(k) \exp(d) en donde k es un entero positivo y d es un número real entre cero y uno, lo que reduce el problema a calcular la función exponencial de un valor entero positivo y un valor entre cero y uno.
- Si c es un entero positivo, entonces, \exp(c) = \mathrm{e}^c = \underbrace{\mathrm{e} \dots \mathrm{e}}_{c \text{ veces}} (utilice su subprograma que calcula la potencia con exponente entero de un número real)
- \sum_{k = 0}^{n} \frac{c^{k}}{k!} \xrightarrow[n \to \infty]{} \exp(c) que se debe utilizar unicamente para calcular la función exponencial de un valor entre cero y uno.
- En esta ocasión, fije la cantidad de términos a usar de la serie. Es decir, primero analice y determine, a lo sumo, cuántos términos son mayores que 1 \times 10^{-15} para c entre 0 y 1, y luego en la implementación use siempre esa misma cantidad de términos.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un número real (c) y que devuelvan una aproximación de la función logaritmo natural evaluada en c \big(\ln(c)\big). Puede tomar \ln\left(2\right) \approx 0.6931471805599453. El subprograma solicitado debe tener en cuenta que:
- Si 0 < c < 1, entonces \ln(c) = -\ln\left(\frac{1}{c}\right), lo que reduce el problema a calcular el logaritmo natural de un valor mayor que uno.
- Si c > 1, entonces \ln(c) = \ln\left((d) \left(2^k\right)\right) = \ln(d) + k \ln\left(2\right), en donde k un entero no negativo y d es un número real entre uno y dos, lo que reduce el problema a calcular el logaritmo natural de un valor entre uno y dos.
- 2 \sum_{k = 0}^{n} \frac{1}{2k+1} \left( \frac{c-1}{c+1} \right)^{2k+1} \xrightarrow[n \to \infty]{} \ln(c) que se debe utilizar unicamente para calcular el logaritmo natural de un valor entre uno y dos.
- En esta ocasión, fije la cantidad de términos a usar de la serie. Es decir, primero analice y determine, a lo sumo, cuántos términos son mayores que 1 \times 10^{-15} para c entre 1 y 2, y luego en la implementación use siempre esa misma cantidad de términos.
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan un valor cercano al número \pi, usando la generación de valores seudoaleatorios / por Monte Carlo. Para el subprograma solicitado pueden usar la función
runif()de R.Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan un valor cercano a la integral definida entre dos números reales dados, de una función de los reales en los reales dada (integrable y bien definida en el intervalo de integración), usando la generación de valores seudoaleatorios / por Monte Carlo (Por ejemplo, consultar Integración de Monte Carlo - Wikipedia). Para el subprograma solicitado pueden usar la función
runif()de R.Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan una aproximación a la integral definida entre dos números reales dados, de una función de los reales en los reales dada (integrable y bien definida en el intervalo de integración), usando el método o regla del trapecio compuesta con todas sus consideraciones (Por ejemplo, consultar Regla del trapecio compuesta. Regla del trapecio - Wikipedia).
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan una aproximación a la integral definida entre dos números reales dados, de una función de los reales en los reales dada (integrable y bien definida en el intervalo de integración), usando el método o regla de Simpson 1/3 compuesta con todas sus consideraciones (Por ejemplo, consultar Regla de Simpson 1/3 compuesta. Regla de Simpson - Wikipedia).
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que devuelvan una aproximación a la integral definida entre dos números reales dados, de una función de los reales en los reales dada (integrable y bien definida en el intervalo de integración), usando el método o regla de Simpson 3/8 compuesta con todas sus consideraciones (Por ejemplo, consultar Regla de Simpson 3/8 compuesta. Regla de Simpson - Wikipedia).
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban un vector de medias y una matriz de covarianzas, y devuelvan una matriz con n filas asociadas a n valores seudoaleatorios provenientes de una vector aleatorio normal multivariado con el vector de medias y la matriz de covarianzas recibidos. Para el subprograma solicitado pueden usar las funciones
rnorm()ychol()de R.-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban una matriz de datos cuantitativos y que devuelvan una lista con: (1) una matriz que tenga los primeros cuatro (r = 1, 2, 3 y 4) momentos no centrales, (2) una matriz que tenga los primeros cuatro momentos centrales, y (3) una matriz que tenga los primeros cuatro momentos estándarizados, de todos y cada uno de los vectores columna de la matriz recibida. Tenga en cuenta que:
Momentos ordinarios o no centrales (población finita de tamaño N):
\gamma'_r = E\left[X^r\right] = \frac{1}{N} \sum_{i=1}^N X_i^r
Note que \gamma'_1 es la media o valor esperado \mu.
Momentos centrales:
\gamma_r = E\left[\left(X - \gamma'_1\right)^r\right] = E\left[\left(X - \mu\right)^r\right]
Por lo tanto,
\begin{align*} \gamma_1 &= \gamma'_1 - \mu = 0 \\ \gamma_2 &= \gamma'_2 - \mu^2 = \sigma^2 \\ \gamma_3 &= \gamma'_3 - 3 \mu \gamma'_2 + 2 \mu^3 \\ \gamma_4 &= \gamma'_4 - 4 \mu \gamma'_3 + 6 \mu^2 \gamma'_2 - 3 \mu^4 \\ &\dots \end{align*}
Note que \gamma_2 es la varianza \sigma^2.
Momentos estándar o estandarizados:
\gamma^*_r = \frac{\gamma_r}{\sigma^r}
Note que \gamma^*_1 = 0, \gamma^*_2 = 1, \gamma^*_3 es el coeficiente de asimetría (Pearson) y \gamma^*_4 es el coeficiente de apuntamiento o curtosis (curtosis de Pearson). El exceso de curtosis (curtosis de Fisher) sería igual a \gamma^*_4 - 3.
-
Un subprograma con una solución de PIEP y uno con una solución de POA (array-oriented) que reciban una matriz de datos cuantitativos y que devuelvan una matriz con todos y cada uno de los vectores columna estandarizados de la matriz recibida.
Si las columnas de una matriz N \times p corresponden a las variables cuantitativas V_1, V_2, \dots, V_p, entonces una matriz con los vectores columna estandarizados sería una matriz N \times p en donde la columna i-ésima sería la variable cuantitativa Z_i = \frac{V_i - \mu_i}{\sigma_i}, donde \mu_i es la media de V_i y \sigma_i es la desviación estándar de V_i (asumamos que los datos que tenemos son poblacionales).