if(!require(knitr)){
install.packages("knitr"); library(knitr)} # tablas fijas
if(!require(plotly)){
install.packages("plotly"); library(plotly)} # gráficos dinámicos1 Introducción
1.1 Generalidades
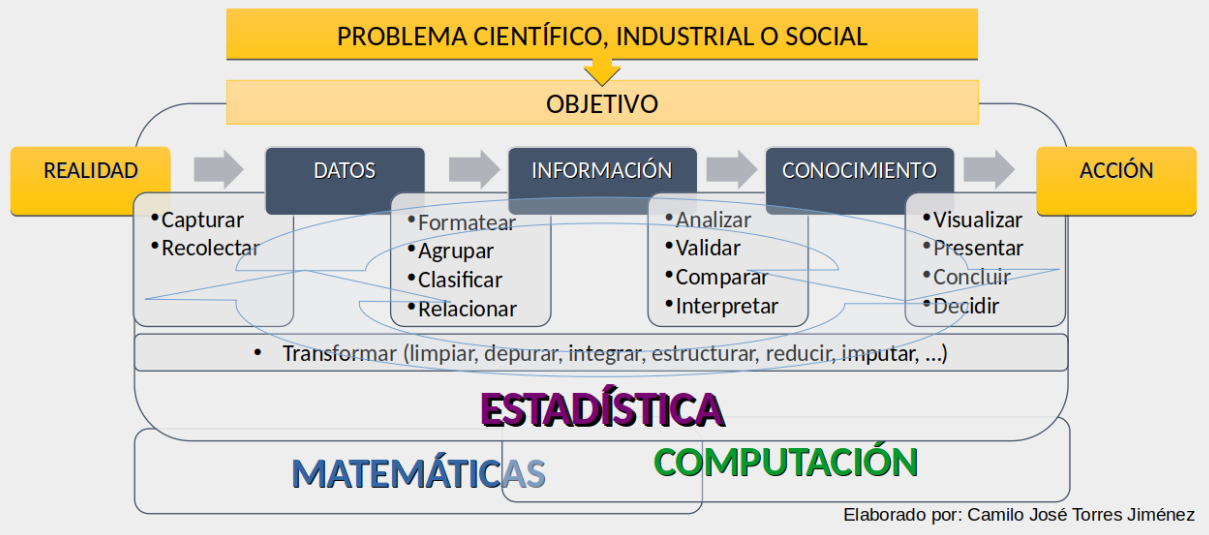
1.1.1 El quehacer de la estadística
1.1.2 Tabla de datos básica
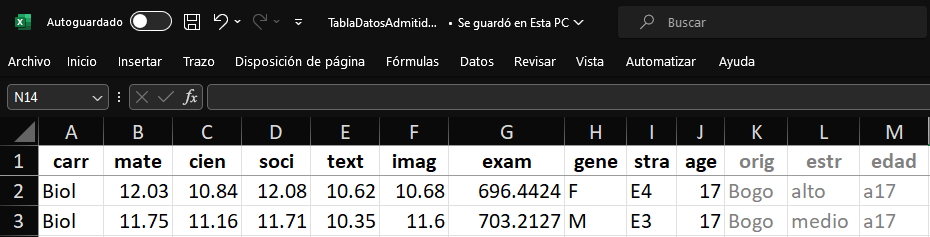
Recordemos que una tabla de datos básica tiene en filas las unidades estadísticas o individuos (observaciones, instancias o registros), y en columnas las variables (características, atributos o features). Así mismo, recordemos su relación con el objeto matemático llamado matriz.
1.1.2.1 Tabla de datos admitidos
Código
if(!require(DT)){
install.packages("DT"); library(DT)} # tablas dinámicas
if(!require(FactoClass)){
install.packages("FactoClass"); library(FactoClass)} # FactoClass
data(admi) # cargar admitidos de FactoClass
Y <- admi[, -c(9,10,11:13,15)]
datatable(Y, style = "bootstrap4",
options = list(pageLength = 3))1.1.3 Relación entre conceptos
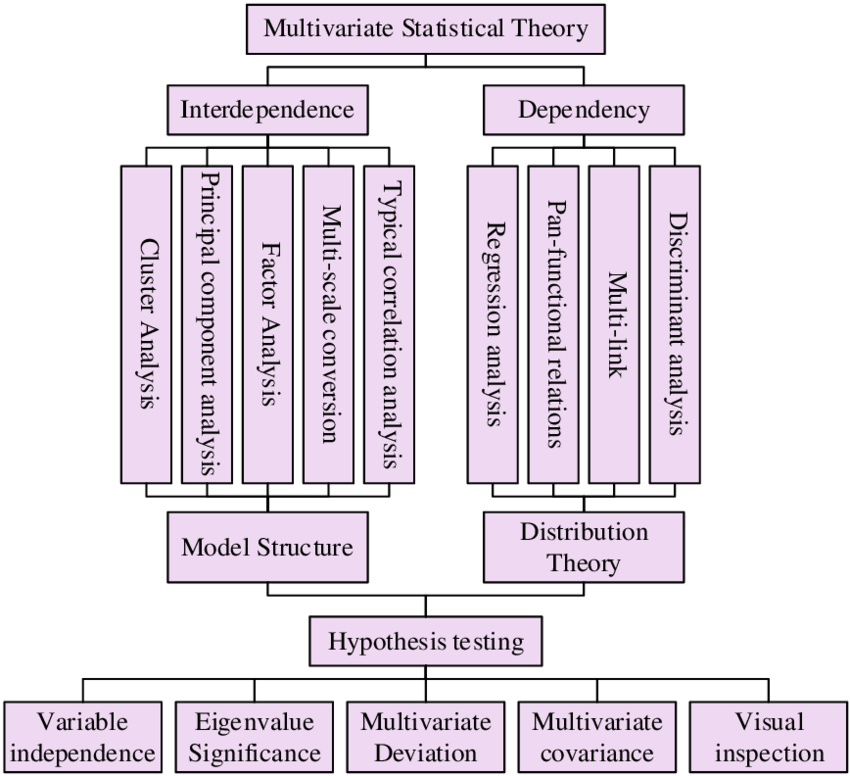
1.1.4 Estadística Multivariada
La estadística multivariada se enfoca en el análisis simultáneo de múltiples variables.
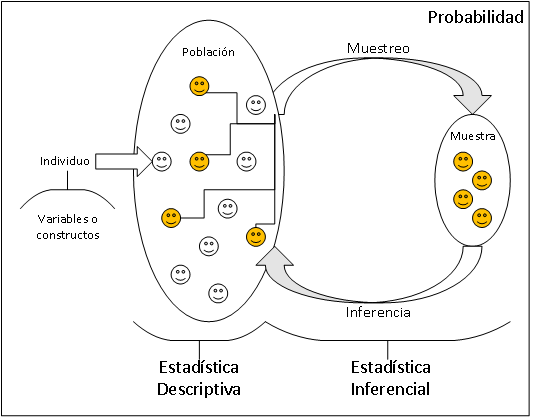
1.1.5 Estadística Descriptiva Multivariada
Los métodos descriptivos y exploratorios multivariados pretenden encontrar significado en grandes tablas de datos.
En Estadística Descriptiva Multivariada NO hay variable(s) “privilegiada(s)” de especial interés, es decir variable(s) respuesta (variable(s) target) a estimar o predecir, eso corresponde a la modelación matemático-estadística y el aprendizaje supervisado.
“Las descripciones multivariadas que recurren a las gráficas para comprender los datos son mucho más difíciles que las univariadas, porque su interpretación correcta depende del conocimiento de los procedimientos y conceptos para su construcción. Los usuarios de diferentes áreas del conocimiento necesitan al menos una comprensión intuitiva de la lógica de los métodos con el fin de lograr la interpretación correcta de las salidas gráficas y de los índices numéricos que las acompañan. Los científicos y profesionales responsables de la metodología estadística deben conocer los fundamentos de la geometría multidimensional, basados en los conceptos del álgebra lineal que tienen que ver con espacios vectoriales en los reales con producto interno.”
Tomado de: Introducción. Pardo, C. (2020). Estadística descriptiva multivariada. Bogotá, Colombia: Universidad Nacional de Colombia. https://repositorio.unal.edu.co/handle/unal/79914
1.1.5.1 Importancia de la Estadística Descriptiva Multivariada
¿qué problemas imagina que surgen al querer analizar 10, 50, 100 o más variables simultáneamente?
if(!require(PerformanceAnalytics)){
install.packages("PerformanceAnalytics"); library(PerformanceAnalytics)}
chart.Correlation(Y[, 2:7], histogram=TRUE, pch=19)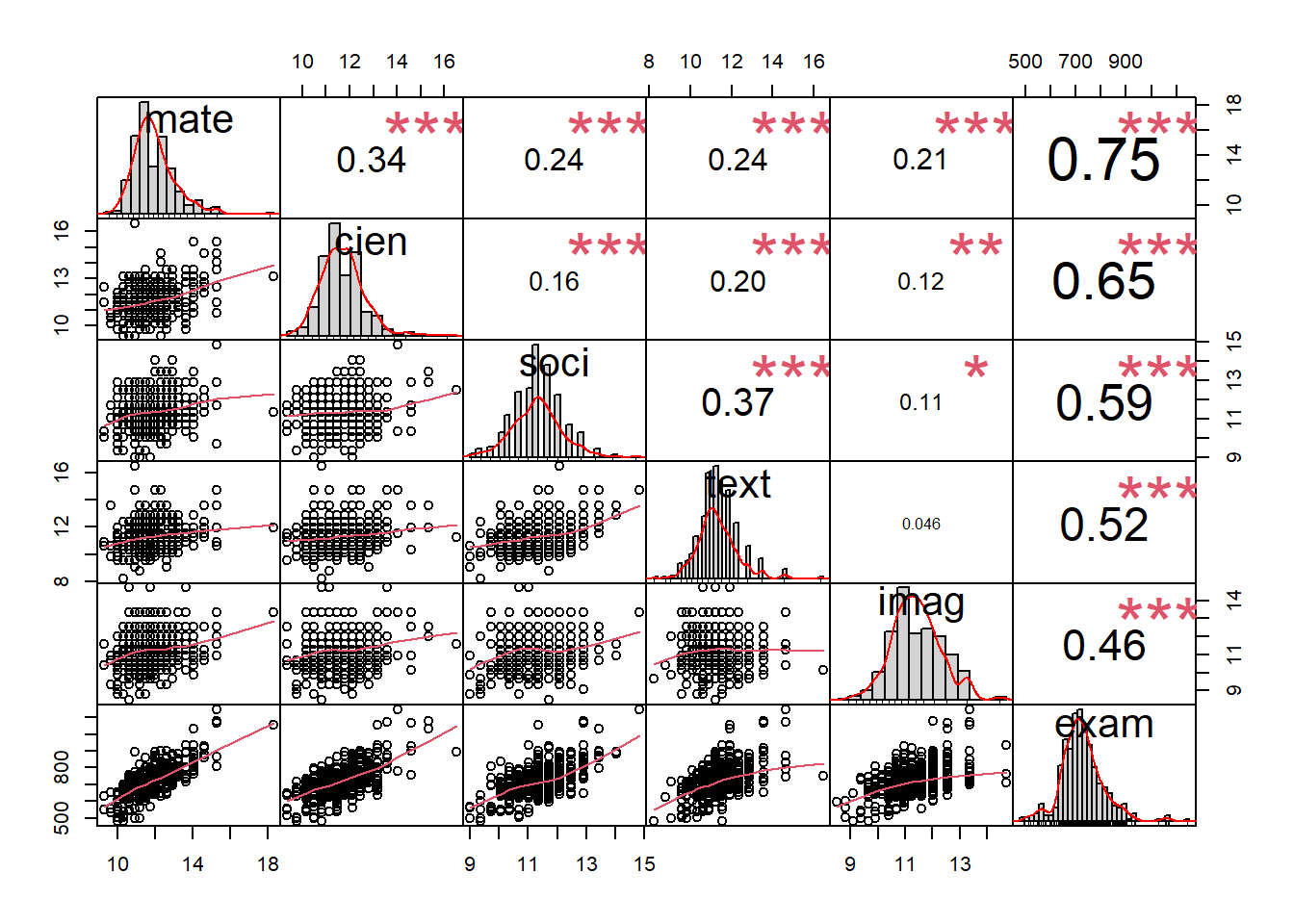
1.2 Dimensión
1.2.1 ¿Dimensión?
Empecemos preguntándonos sobre el concepto mismo de dimensión.
Discusión: ¿qué nos dice nuestra intuición? ¿cuántas dimensiones cree que tienen los siguientes objetos?




¿y en estos casos?

Existen: dimensión de un espacio vectorial, dimensión topológica, dimensión de Krull, dimensiones fractales (p.ej. la dimensión de Hausdorff), etc.
¿y la dimensión de nuestros datos?
En ambos casos tenemos un conjunto de datos con tres variables (tres dimensiones). Sin embargo, si se “miran adecuadamente”, puede que los datos “vivan” o queden “bien representados” en una dimensión menor. ¿Y si tenemos muchas más de tres variables?
1.2.2 Maldición de la dimensión
La maldición de la dimensión (Curse of Dimensionality) se refiere a los problemas y las complicaciones que aparecen al trabajar con datos en muchas dimensiones. A medida que tenemos más variables, tenemos más dimensiones (por ejemplo, d = 20, 100, \dots), y los “volúmenes” (hipervolúmenes) sobre esos espacios d-dimensionales son cada vez más grandes (exponencialmente más grandes con respecto al aumento de dimensiones).
| Complicaciones: | ||
|---|---|---|
|
|
|
|
|
|
1.2.3 Reducción de la dimensión
La principal solución a la maldición de la dimensión es la reducción de la dimensión.
Al reducir la dimensión, podemos conservar la información más importante en los datos mientras descartamos las características redundantes o menos importantes.