3 ACP generalizado
Código a ejecutar antes de empezar:
El análisis en componentes principales (ACP) canónico, descrito en la sección anterior, se apoya en la geometría euclidiana, canónica o usual.
En esta sección se hace una extensión que sirve para poner en un marco de referencia común, a los métodos denominados factoriales, dentro de los cuales están el ACP canónico y los análisis de correspondencias simples y múltiples. Dicha extensión se denomina ACP generalizado o general.
3.1 Métrica
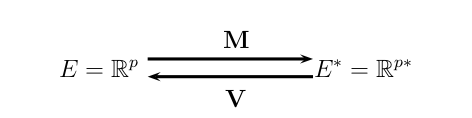
Sea M matriz que define un producto interno en un espacio vectorial en los reales, E. A partir de M se dota al espacio de una geometría Euclidiana.
Sean x y y dos vectores en E, entonces:
M-producto punto: \left\langle \mathbf{x},\mathbf{y} \right\rangle_{\mathbf{M}} = \mathbf{x'My} = \mathbf{y'Mx}
M-norma: \| \mathbf{x} \|^2_{\mathbf{M}} = \left\langle \mathbf{x} , \mathbf{x} \right\rangle_{\mathbf{M}}
M-distancia: d_{\mathbf{M}}(\mathbf{x},\mathbf{y}) = \| \mathbf{x} - \mathbf{y} \|_{\mathbf{M}}
Vector M-unitario: 1 = \| \mathbf{u} \|_{\mathbf{M}} = \mathbf{u'Mu}
M-proyección sobre u: \left\langle \mathbf{x} , \mathbf{u} \right\rangle_{\mathbf{M}} = \mathbf{x'Mu}
M-coseno: \cos_{\mathbf{M}} \left(\angle_\mathbf{x}^\mathbf{y} \right) = \dfrac{\left\langle\mathbf{x},\mathbf{y} \right\rangle_{\mathbf{M}}}{\| \mathbf{x} \|_{\mathbf{M}} \; \| \mathbf{y} \|_{\mathbf{M}} }
M-ortogonal: 0 = \left\langle\mathbf{x},\mathbf{y} \right\rangle_{\mathbf{M}} = \mathbf{x'My}
3.2 ACP(X, M, N)
\boldsymbol{ X_{n \times p} \; : }
Matriz de n filas y p columnas, obtenida mediante alguna transformación de los datos, dependiendo del análisis a realizar.
\boldsymbol{ M_{p \times p} \; : }
Matriz diagonal de tamaño p (matriz de p valores en la diagonal y ceros fuera de la diagonal). En la diagonal están los pesos de las columnas (variables).
\boldsymbol{ N_{n \times n} \; : }
Matriz diagonal con los pesos de las filas (individuos).
La relación de esas matrices garantiza la dualidad entre los dos espacios. Es así que un ACP generalizado ACP(X, M, N) queda determinado por su respectiva tripleta de matrices.
X, M y N del ACP canónico:
La matriz de trabajo ( X ) es la matriz de datos solamente centrada (X = Y_C) (ACP no normado) o estandarizada (X = Y_C \, D_{\sigma}^{-1}) (ACP normado).
-
Los pesos de las variables se evidencian en la distancia euclidiana entre individuos,
\begin{aligned} d^2(\vec{y}_i,\vec{y}_l) &= ( y_{i1} - y_{l1} )^2 + ( y_{i2} - y_{l2} )^2 + \dots + ( y_{ip} - y_{lp} )^2 \end{aligned}
-
Los pesos de los individuos se evidencian en el cálculo del centro de gravedad,
\begin{aligned} \vec{\mathrm{g}} &= \tfrac{1}{n} \vec{y}_1 + \tfrac{1}{n} \vec{y}_2 + \dots + \tfrac{1}{n} \vec{y}_n \end{aligned}
Por lo tanto, el ACP canónico (normado) se puede escribir como el ACP generalizado:
ACP\left(X = Y_C \, D_{\sigma}^{-1} \, , \, M = I_p \, , \, N = \frac{1}{n} I_n\right)
3.3 Diagrama de dualidad
El diagrama de dualidad presenta una serie de transformaciones lineales que permiten pasar de un espacio a otro. Las transformaciones lineales están definidas por las matrices X, M, N y derivadas de ellas: inversas, cuando existen; y composiciones de ellas. A continuación se presenta el diagrama de dualidad.
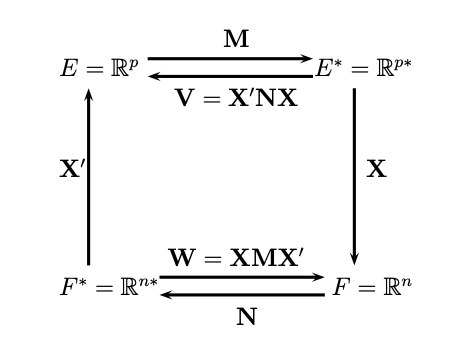
Los cuatro espacios vectoriales del diagrama son:
E = \mathbb{R}^p: espacio de las filas, su base canónica son las columnas de la matriz identidad I_p.
E^{*} = \mathbb{R}^{p*}: espacio dual de las filas.
F = \mathbb{R}^n: espacio de las columnas, su base canónica son las columnas de la matriz identidad I_n.
F^{*} = \mathbb{R}^{n*}: espacio dual de las columnas.
Desde el punto de vista de la geometría euclidiana multidimensional, el ACP generalizado realiza una rotación ortogonal del sistema de ejes, lo que es también un cambio de base.
Note que en el espacio de las filas E \xrightarrow{ \mathbf{X'NXM}} E, Inercia = traza(\mathbf{X'NXM}) y \mathbf{X'NXM} es la matriz a la que se le hallan los valores y vectores propios.
3.4 Fórmulas
Con las fórmulas asociadas al diagrama de dualidad se obtienen las de cualquier método factorial al reemplazar por las matrices que correspondan en cada caso.
3.4.1 Antes de la rotación
.png)
3.4.2 Después de la rotación
2.png)
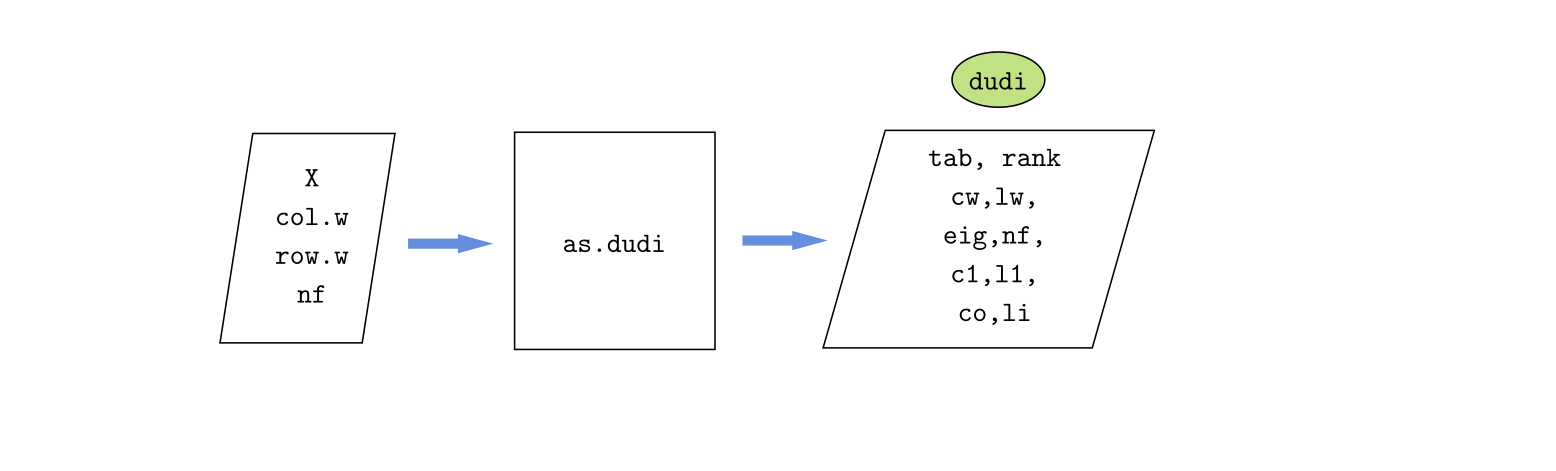
3.4.3 Función as.dudi{ade4}
as.dudi es una función del paquete ade4 para obtener un ACP generalizado (consultar la ayuda respectiva).
3.5 Imagen matriz de covarianzas y de correlaciones
Podemos usar el ACP generalizado para producir una representación gráfica de la relación lineal entre variables, directamente de una matriz de varianzas y covarianzas o de una matriz de correlaciones (¿mejor que un mapa de calor?).
En este caso suponemos que no se dispone de la matriz de datos (X), pero sí de la matriz de correlaciones (análisis normado) o de varianzas y covarianzas (análisis no normado) (V).
Como V = X'NX y M = I_p entonces, X'NXI_p = V es la matriz de inercia de la nube de individuos.
Las coordenadas de las variables sobre un eje se pueden obtener directamente a partir de los vectores propios de la matriz de inercia de la nube de individuos (de la matriz V), así, G_s = \sqrt{\lambda_s} \mathbf{u}_s
Supongamos que no tenemos la matriz de datos sino la siguiente matriz de varianzas y covarianzas:
kable(as.data.frame(Vcov), digits = 3)| mate | cien | soci | text | imag | |
|---|---|---|---|---|---|
| mate | 1.287 | 0.387 | 0.238 | 0.272 | 0.240 |
| cien | 0.387 | 1.002 | 0.138 | 0.201 | 0.123 |
| soci | 0.238 | 0.138 | 0.750 | 0.319 | 0.091 |
| text | 0.272 | 0.201 | 0.319 | 0.985 | 0.046 |
| imag | 0.240 | 0.123 | 0.091 | 0.046 | 1.008 |
eigV <- eigen(Vcov)
Lambda <- diag(eigV$values)
U <- eigV$vectors
G <- U %*% sqrt(Lambda)
rownames(G) <- colnames(Vcov)
colnames(G) <- paste("G", 1:5, sep = "")
kable(t(G[,1:2]), digits = 2) # Coordenadas primer plano| mate | cien | soci | text | imag | |
|---|---|---|---|---|---|
| G1 | -0.93 | -0.63 | -0.44 | -0.57 | -0.40 |
| G2 | -0.19 | -0.02 | 0.31 | 0.60 | -0.71 |
s.arrow(G)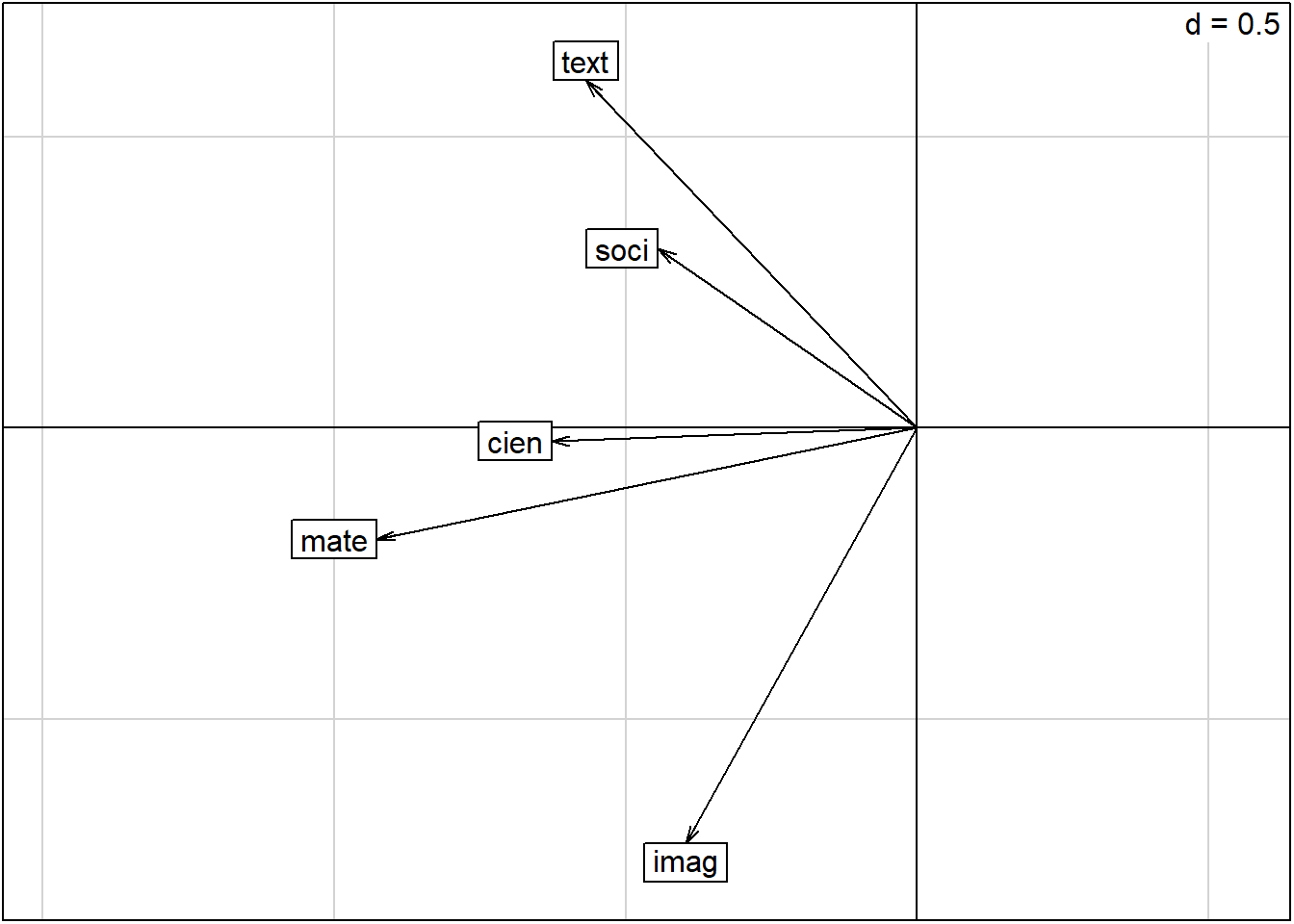
Supongamos que no tenemos la matriz de datos sino la siguiente matriz de correlaciones:
kable(as.data.frame(Vcor), digits = 3)| mate | cien | soci | text | imag | |
|---|---|---|---|---|---|
| mate | 1.000 | 0.341 | 0.242 | 0.242 | 0.211 |
| cien | 0.341 | 1.000 | 0.160 | 0.202 | 0.123 |
| soci | 0.242 | 0.160 | 1.000 | 0.372 | 0.105 |
| text | 0.242 | 0.202 | 0.372 | 1.000 | 0.046 |
| imag | 0.211 | 0.123 | 0.105 | 0.046 | 1.000 |
eigV <- eigen(Vcor)
Lambda <- diag(eigV$values)
U <- eigV$vectors
G <- U %*% sqrt(Lambda)
rownames(G) <- colnames(Vcor)
colnames(G) <- paste("G", 1:5, sep = "")
kable(t(G[,1:2]), digits = 2) # Coordenadas primer plano| mate | cien | soci | text | imag | |
|---|---|---|---|---|---|
| G1 | -0.71 | -0.61 | -0.64 | -0.65 | -0.38 |
| G2 | -0.26 | -0.24 | 0.42 | 0.50 | -0.69 |
s.corcircle(G, fullcircle = F)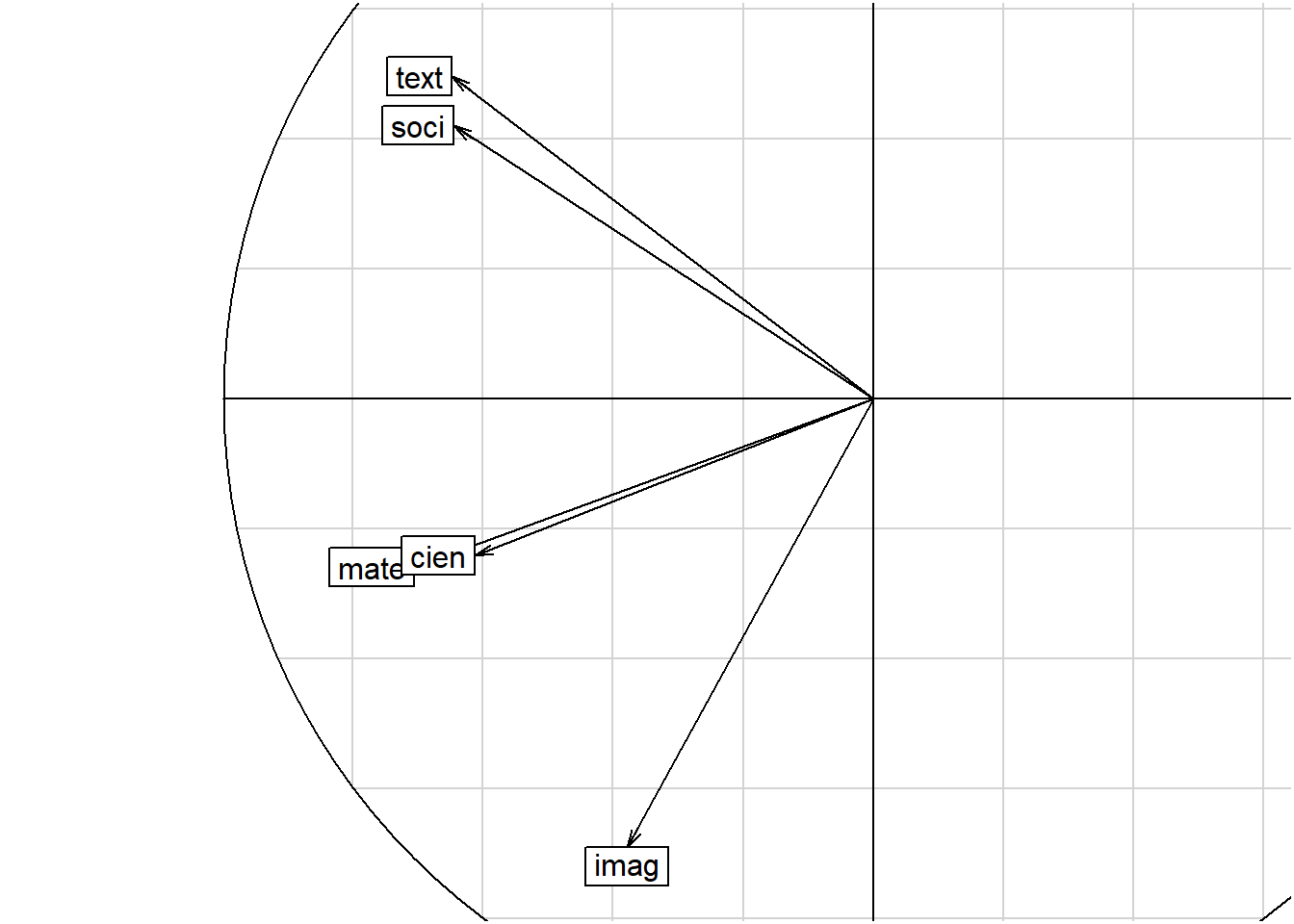
Una imagen de este tipo permite visualizar la relación entre variables (en este caso, dada por la matriz de correlaciones) e incluso podría permitir el establecer grupos de variables.
3.6 Análisis en coordenadas principales
Cuando se tienen matrices de distancias euclidianas entre todos los individuos de un estudio, también se pueden obtener imágenes euclidianas de estas matrices. El procedimiento es obtener primero, la matriz de productos escalares entre individuos W, luego encontrar la matriz WN y hallar sus valores y vectores propios: \lambda_s, \ \mathbf{v}_s\ : \ \ s=1,2 \cdots S.
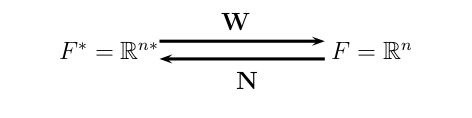
Las coordenadas de los individuos sobre un eje se obtienen mediante: F_s = \sqrt{\lambda_s} \mathbf{v}_s
Supongamos que no tenemos la matriz de datos sino la siguiente matriz de distancias:
round(D, 1) ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C Com1
C40M 9.1
C40C 7.8 2.6
C20M 6.0 4.2 3.4
C20C 4.7 5.6 3.8 2.9
ExOs 4.4 9.6 7.8 7.1 5.6
O40M 10.0 4.2 4.0 6.0 6.7 9.1
O40C 8.3 5.3 3.6 5.6 5.4 6.9 3.8
O20M 6.4 6.3 4.4 5.0 4.2 4.4 5.3 3.2
O20C 5.7 7.0 5.2 5.5 4.5 3.6 6.0 3.8 2.2
Com1 6.2 6.8 5.8 5.3 4.5 5.8 7.0 6.4 5.0 4.5
Com2 5.0 8.3 7.2 6.0 4.8 6.0 8.9 7.6 6.2 5.8 3.9
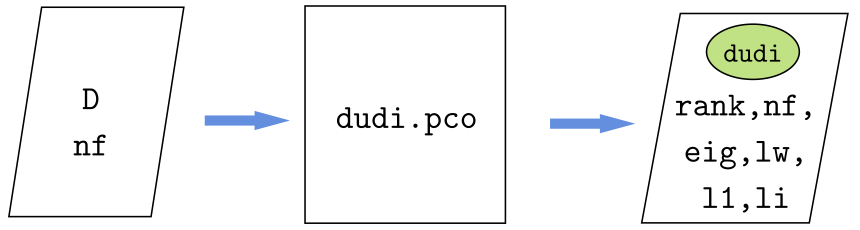
3.6.1 Función dudi.pco{ade4}
dudi.pco es una función del paquete ade4 para obtener un análisis en coordenadas principales.
(aco <- dudi.pco(D, scannf=FALSE, nf = n))Duality diagramm
class: pco dudi
$call: dudi.pco(d = D, scannf = FALSE, nf = n)
$nf: 11 axis-components saved
$rank: 11
eigen values: 8.755 3.553 1.889 0.5605 0.4454 ...
vector length mode content
1 $cw 11 numeric column weights
2 $lw 12 numeric row weights
3 $eig 11 numeric eigen values
data.frame nrow ncol content
1 $tab 12 11 modified array
2 $li 12 11 row coordinates
3 $l1 12 11 row normed scores
4 $co 11 11 column coordinates
5 $c1 11 11 column normed scores
other elements: NULLiner <- inertia(aco)$tot.inertia
corte <- mean(iner$inertia)
kable(iner[iner$inertia > corte, ],
digits = 2)| inertia | cum | cum(%) | |
|---|---|---|---|
| Ax1 | 8.76 | 8.76 | 54.72 |
| Ax2 | 3.55 | 12.31 | 76.93 |
| Ax3 | 1.89 | 14.20 | 88.74 |
attributes(aco)$class <- c("pca","dudi")
fviz_eig(aco, addlabels = TRUE)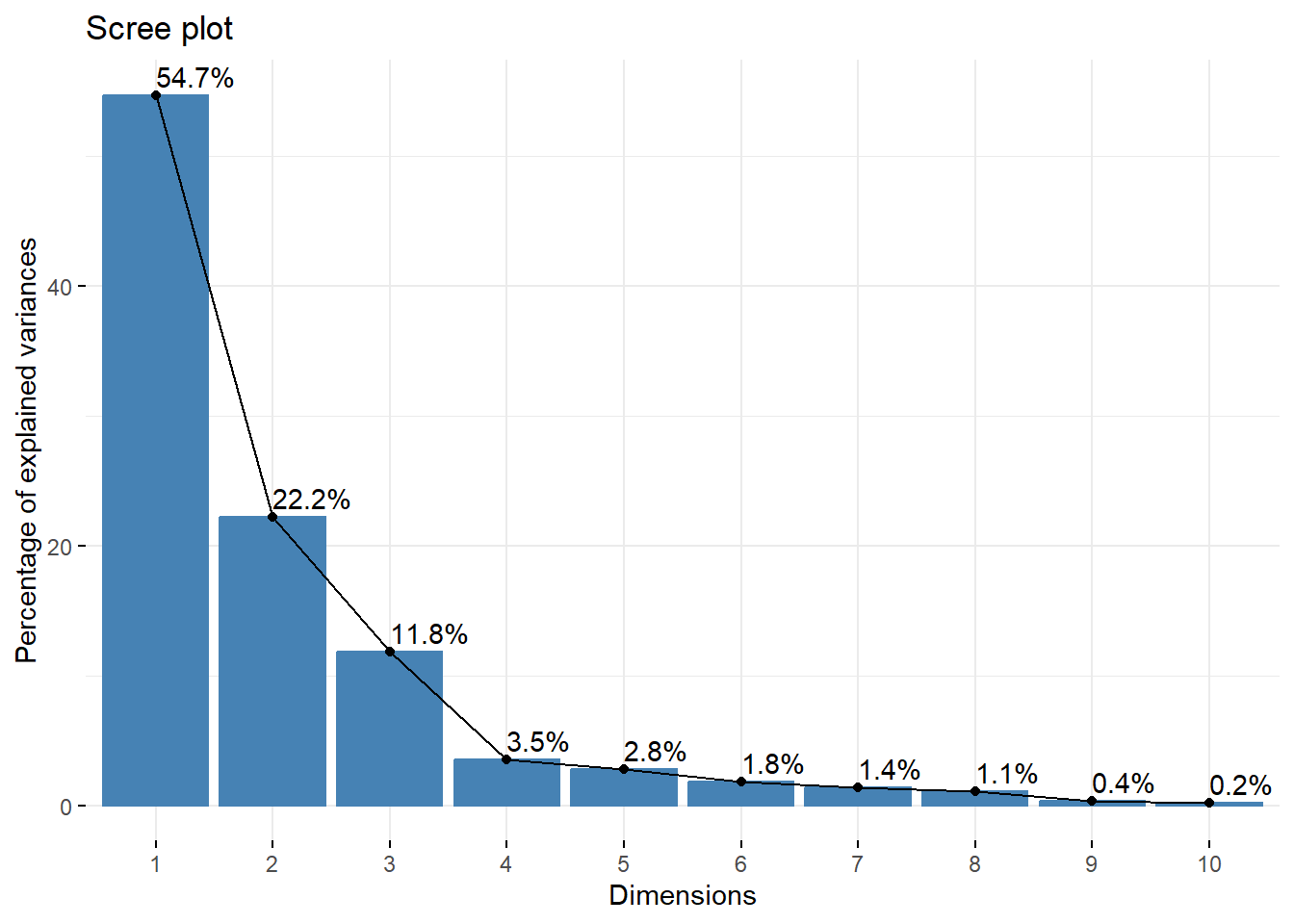
Primeras tres componentes:
library(plotly)
fig <- plot_ly(aco$li, x = ~A1, y = ~A2, z = ~A3)
fig <- fig %>% add_markers(text = rownames(aco$li))
fig <- fig %>% add_text(text = rownames(aco$li))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)
fig <- fig %>% layout(showlegend = FALSE)
figPlanos factoriales
plot(aco, gg=T, Tcol=FALSE, col.row=4)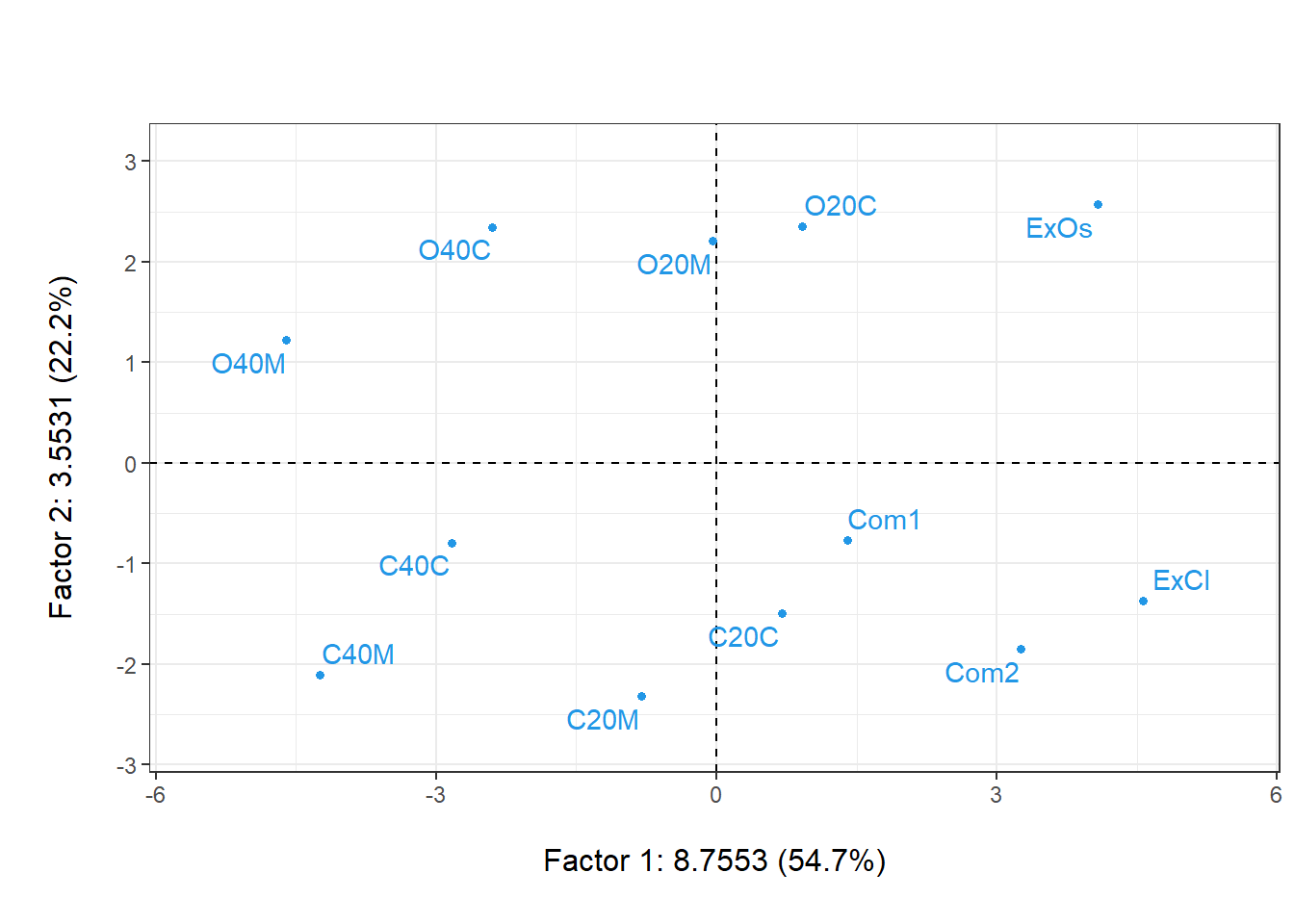
plot(aco, 3, 2, gg=T, Tcol=FALSE, col.row=4)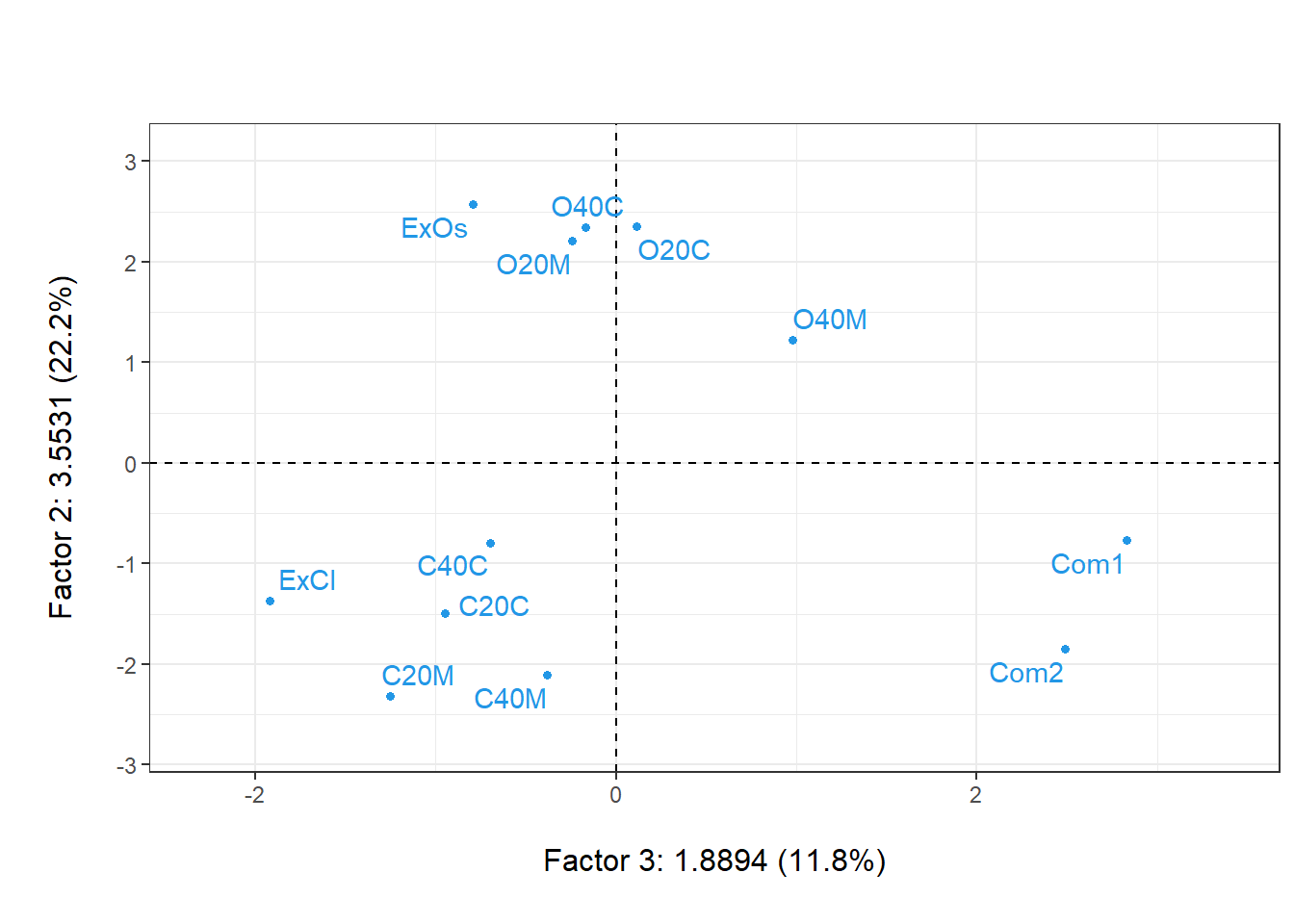
En este caso, todo lo que se puede hacer y lograr con un ACP canónico para una nube de individuos, también se puede realizar con el análisis en coordenadas principales de una matriz de distancias euclidianas.