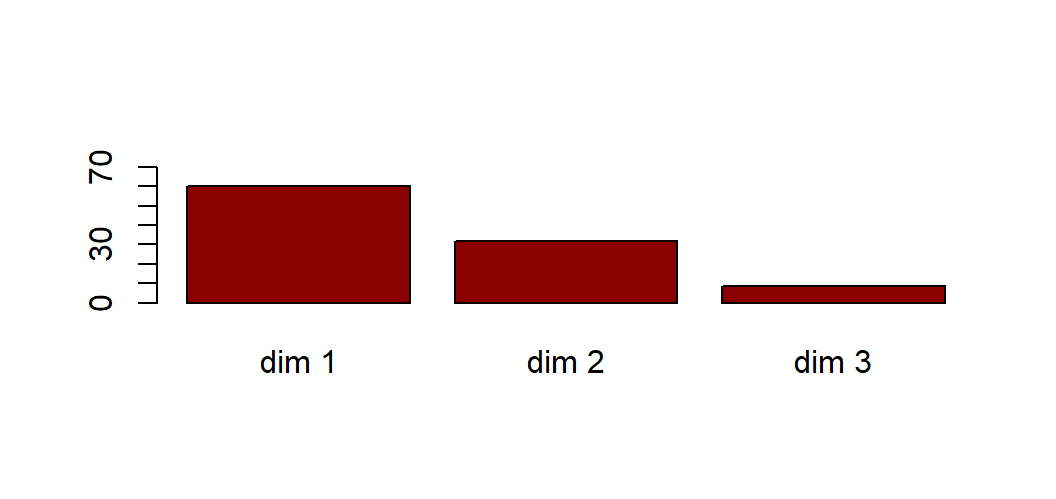# cambia idioma de la consola de R a español:
Sys.setenv(LANG="es")
# usar 2 cifras significativas y tiende a evitar
# notación científica (ver ayuda de función: `options`):
options(digits = 2, scipen = 999)
# cargar librerías:
if(!require(FactoClass)){
install.packages("FactoClass"); library(FactoClass)}
if(!require(Factoshiny)){
install.packages("Factoshiny"); library(Factoshiny)}
if(!require(factoextra)){
install.packages("factoextra"); library(factoextra)}
if(!require(plotly)){
install.packages("plotly"); library(plotly)} # gráficos dinámicos5 ACM
Ver Capítulo 6 de: Pardo, C. (2020). Estadística descriptiva multivariada. https://repositorio.unal.edu.co/handle/unal/79914
Código a ejecutar antes de empezar:
5.1 Introducción
El análisis de correspondencias múltiples (ACM) se utiliza para analizar tablas de individuos descritos por variables cualitativas.
Para cada individuo, cada variable debe tener como valor solamente una opción o categoría (“selección múltiple con única respuesta”).
El ACM es una extensión del ACS con propiedades muy particulares.
Dependiendo del objetivo del análisis, las variables de uno de los temas suelen jugar el papel de variables activas para el análisis.
El ACM nos permite:
- Descubrir asociaciones entre categorías de las variables.
- Identificar posibles patrones en los individuos.
- Estudiar la relación entre las categorías de las variables activas y elementos ilustrativos o suplementarios.
El ACM también se puede usar para:
- Reducir la dimensión.
- Separar información de “ruido”.
- Dar valores numéricos a las categorías.
De lo anterior se deduce que uno de los posibles usos del ACM es como un pretratamiento de los datos, para aplicar luego métodos estadísticos multivariados aptos para variables continuas (como por ejemplo, regresión o algunos métodos de agrupamiento y de discriminación).
5.2 Ejemplo de “juguete” (admitidos)
Supongamos que los objetivos de análisis son describir el espacio sociodemográfico de los admitidos, y explorar las diferencias en las condiciones sociodemográficas, entre los grupos de admitidos según las carreras.
Se utilizan como variables activas, las sociodemográficas disponibles:
-
Género (
gene): Femenino, Masculino -
Edad (
edad): 16 o menos, 17, 18, 19 o más -
Estrato (
estr): bajo, medio, alto -
Procedencia (
orig): Bogotá, Cundinamarca, Otro
IMPORTANTE: No olvidemos que en R, las variables cualitativas siempre deberían ser de tipo de dato factor.
5.2.1 Tabla de código condensado (Y)
Las filas representan los (n) individuos y las columnas las (s) variables cualitativas. Note que esta tabla no tiene significado numérico.
5.2.2 Tabla disyuntiva completa (TDC) (Z)
La TDC es una tabla binaria, que sigue teniendo por filas los individuos, pero por columnas tiene todas las (p) categorías. ¿Qué significarán el uno o cero en cada celda?
Código
Z <- acm.disjonctif(Y) # función de ade45.2.3 Tabla de Burt (B)
La tabla de Burt o tabla de contingencias múltiples es la matriz cuadrada y simétrica: B = Z^T Z. ¿Qué significarán los números en cada celda?
ge.F ge.M ed.a16m ed.a17 ed.a18 ed.a19M es.baj es.med es.alt or.Bog or.Cun or.Otr
ge.F 128 0 46 45 18 19 46 59 23 89 9 30
ge.M 0 317 72 126 38 81 133 126 58 222 29 66
ed.a16m 46 72 118 0 0 0 44 47 27 70 9 39
ed.a17 45 126 0 171 0 0 58 74 39 116 19 36
ed.a18 18 38 0 0 56 0 22 26 8 47 2 7
ed.a19M 19 81 0 0 0 100 55 38 7 78 8 14
es.baj 46 133 44 58 22 55 179 0 0 95 22 62
es.med 59 126 47 74 26 38 0 185 0 151 11 23
es.alt 23 58 27 39 8 7 0 0 81 65 5 11
or.Bog 89 222 70 116 47 78 95 151 65 311 0 0
or.Cun 9 29 9 19 2 8 22 11 5 0 38 0
or.Otr 30 66 39 36 7 14 62 23 11 0 0 965.3 El ACM como un ACS de la TDC
El ACM se podría ver como un ACS de la tabla disyuntiva completa o de la tabla de Burt. Sin embargo, en el segundo caso se perdería la información de los individuos. Por tal razón, es mejor verlo como un ACS de la TDC.
Teniendo en cuenta lo anterior, el ACP generalizado correspondiente para las filas (los individuos) sería:
ACP\left(X = \tfrac{1}{s} Z \, , \, M = n s D_{p}^{-1} \, , \, N = \tfrac{1}{n} I_{n}\right)
Planos factoriales de los individuos:
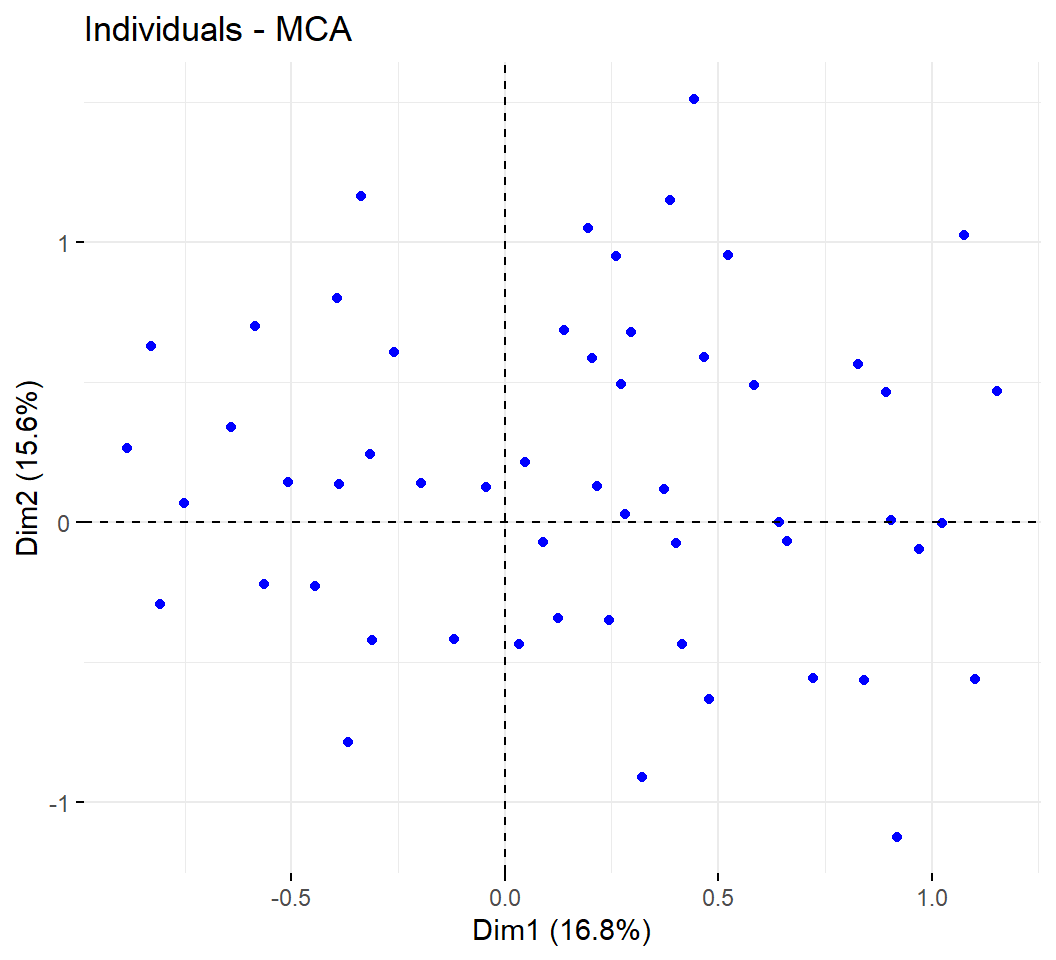
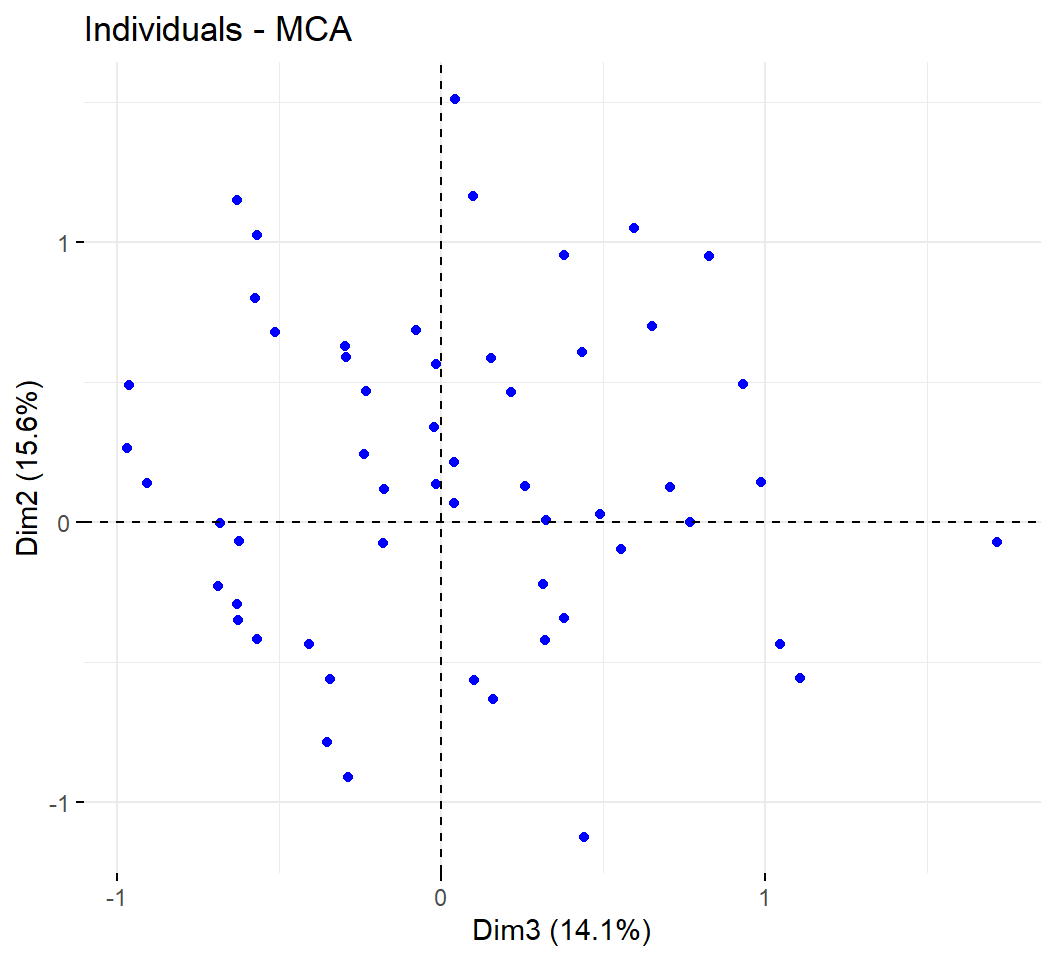
Del análisis de las filas (los individuos) concluimos que:
Dos individuos se parecen cuando asumen más o menos las mismas categorías. La distancia se amplifica más cuando uno solo de los dos individuos asume una categoría de baja frecuencia.
La inercia de la nube de individuos depende del cociente entre el número de categorías y el número de variables \left( \tfrac{p}{s} - 1\right), no de los valores internos de la tabla. Por lo tanto, no tiene significado estadístico.
En el ACM se pone más atención a las categorías, porque los individuos son anónimos en la mayoría de las aplicaciones.
Planos factoriales de las categorías:
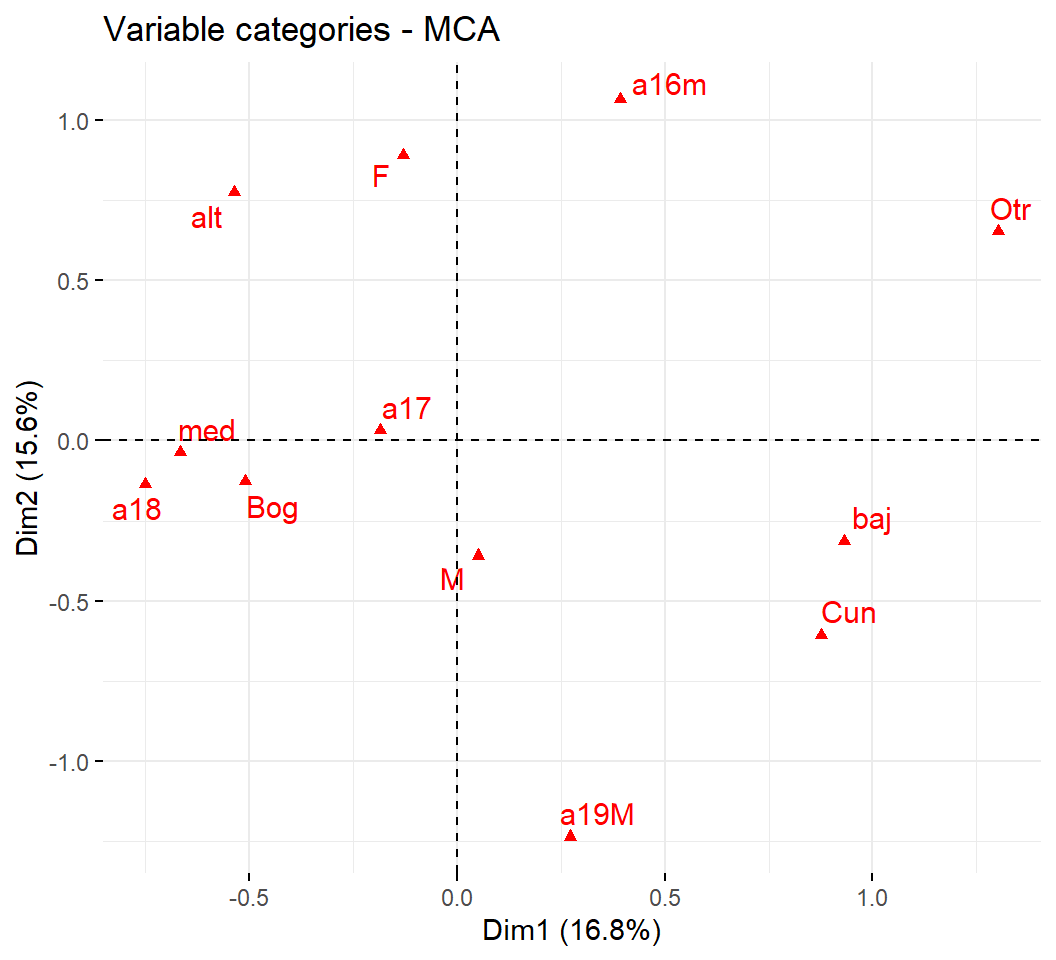
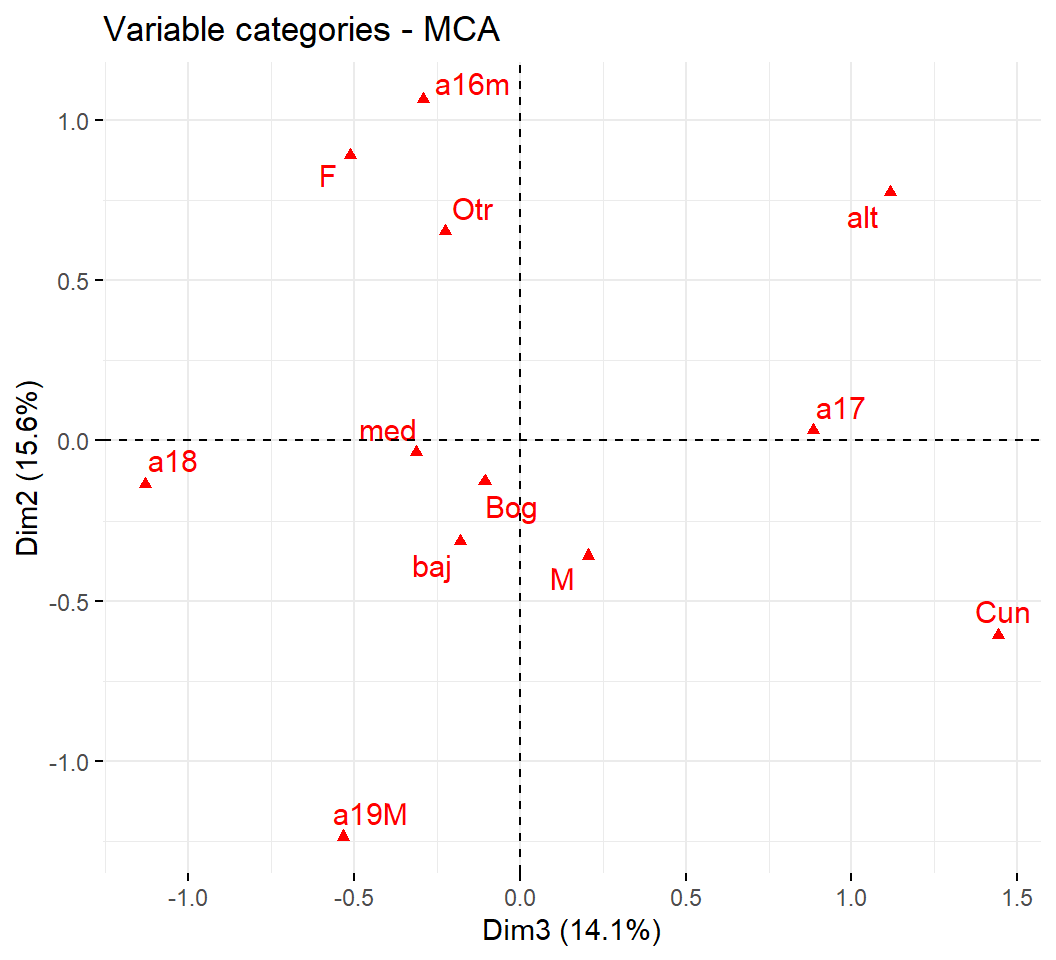
Del análisis de las categorías concluimos que:
La inercia de la nube de categorías es la misma que la de la nube de individuos, que como ya se mencionó, no tiene significado estadístico.
Las variables con más número de categorías contribuyen más a la inercia.
Por otro lado, las categorías de baja frecuencia contribuyen más a la inercia. En consecuencia, las categorías de menores frecuencias son las más alejadas del origen.
5.4 El ACM como un ACP de la TDC
El ACM también se podría ver como un ACP de la tabla disyuntiva completa.
Bajo esta visión, el ACP generalizado correspondiente sería:
ACP\left(X = n Z D_{p}^{-1} \, , \, M = \tfrac{1}{n s} D_{p} \, , \, N = \tfrac{1}{n} I_{n}\right)
Las fórmulas de transición que se obtienen a partir de este ACP, que son las mismas relaciones cuasibaricéntricas que se obtienen del mencionado ACS de la TDC, permiten la representación simultanea de la nube de individuos y la nube de categorías.
Código
# OPCIÓN 1:
library("FactoMineR")
acm <- MCA(Y, graph=FALSE)Código
# OPCIÓN 2:
library("Factoshiny") # cargar Factoshiny
res <- MCAshiny(admi) # activar ACM para admiRepresentaciones simultaneas:
Código
fviz_mca_biplot(acm, axes=c(1,2),
repel = TRUE, label = "var",
ggtheme=theme_minimal())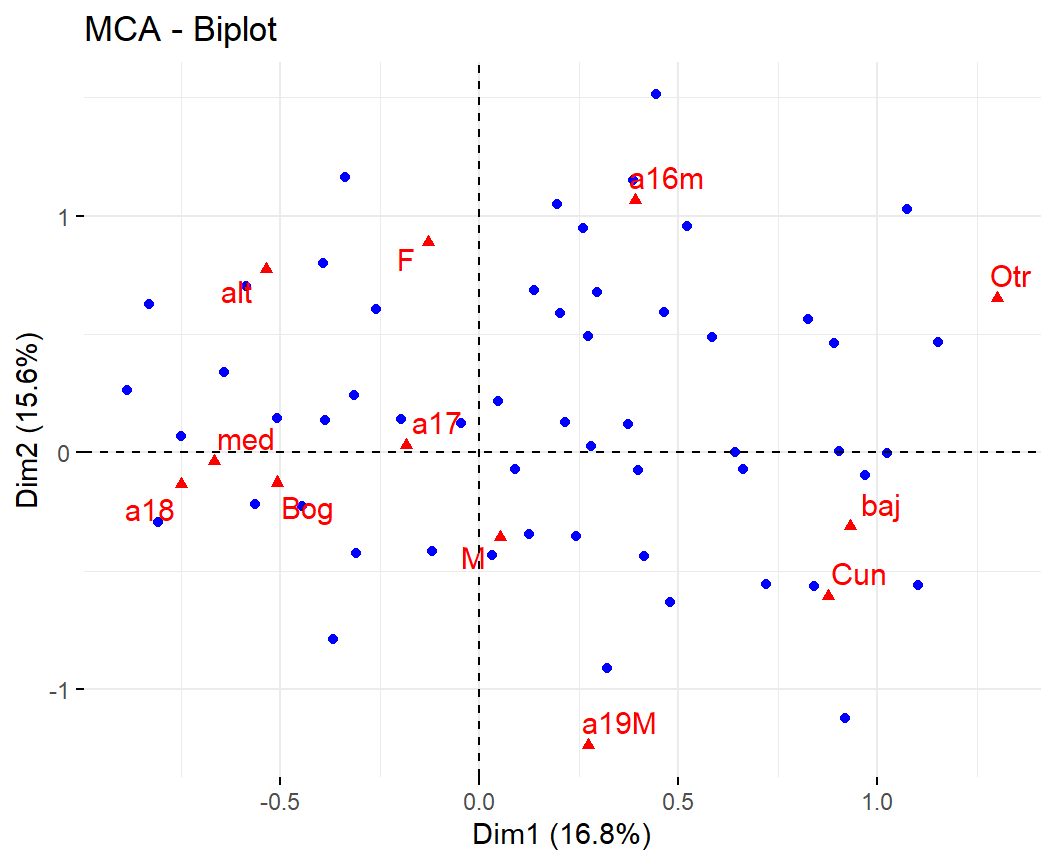
Código
fviz_mca_biplot(acm, axes=c(3,2),
repel = TRUE, label = "var",
ggtheme=theme_minimal())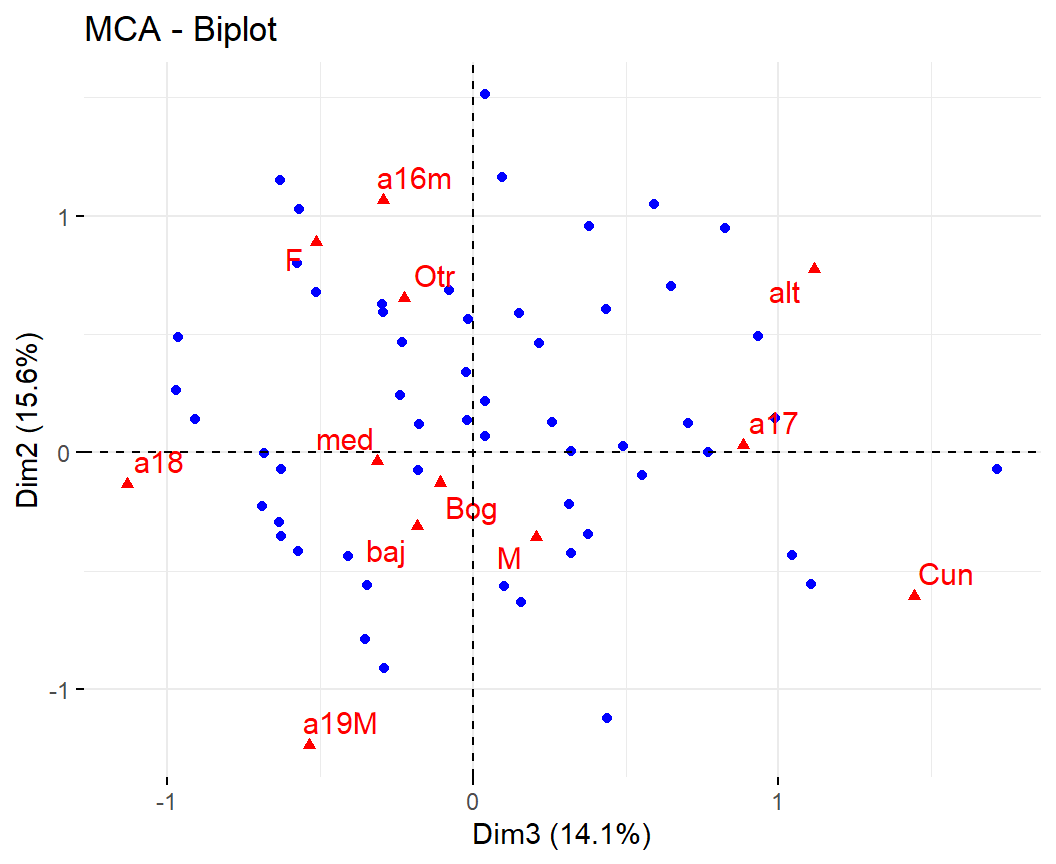
5.5 El criterio de Benzécri
El ACM tiene ejes que se pueden considerar “parásitos”, en el sentido en que realmente no están aportando información. Por lo tanto, el porcentaje de inercia no es un criterio apropiado en el caso del ACM.
Benzécri propuso considerar solamente los ejes asociados a valores propios superiores al inverso multiplicativo del número de variables y recalcular las tasas de inercia mediante la fórmula: \tau(\lambda) = \left(\tfrac{s}{s-1}\right)^2 \left(\lambda-\tfrac{1}{s}\right)^2 para \lambda > \tfrac{1}{s}.
fviz_screeplot(acm, addlabels = TRUE, ylim = c(0, 20))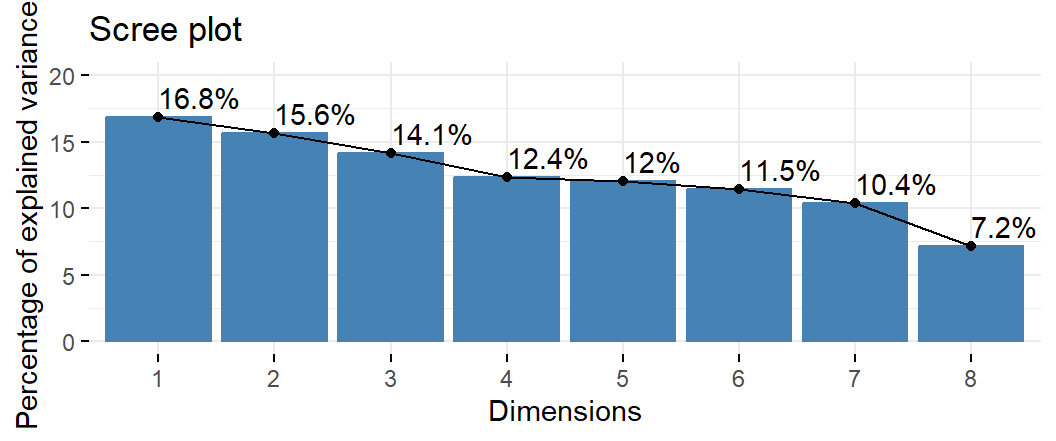
5.6 Ayudas para la interpretación
Las ayudas para la interpretación de los individuos y de las categorías tienen las mismas expresiones que las del ACP y ACS. No olvide consultar la ayudas numéricas (incluso antes de escoger qué gráficos va a producir), especialmente los valores test para identificar cuándo las diferencias SON o NO SON significativas con respeto al centro de gravedad.
fviz_contrib(acm, choice = "var", axes = 1)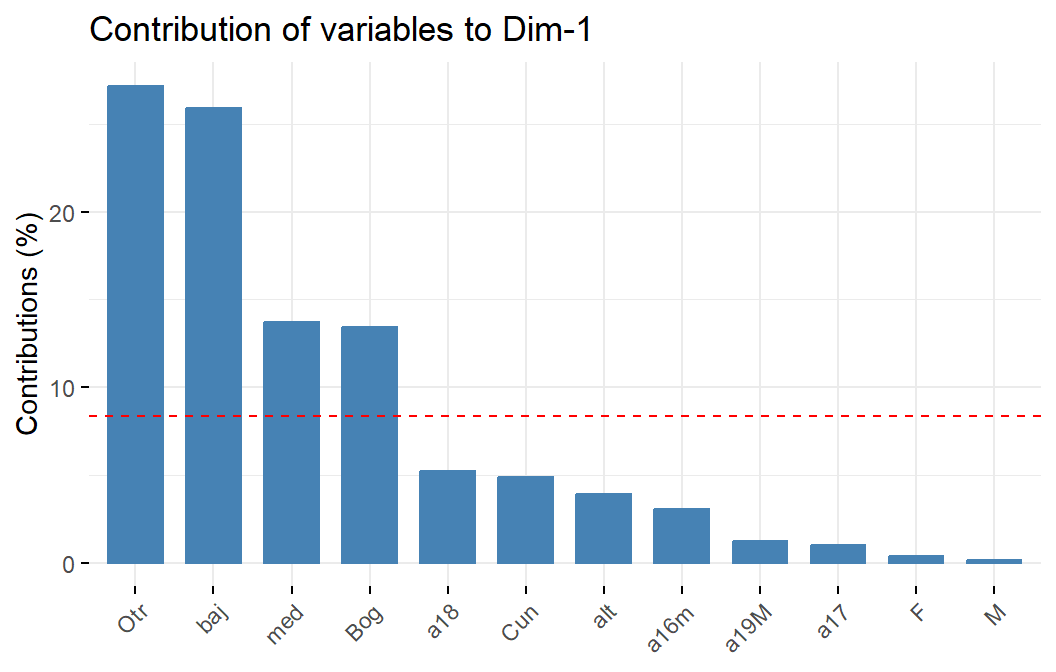
fviz_mca_var(acm, col.var = "cos2", repel = TRUE,
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
ggtheme = theme_minimal())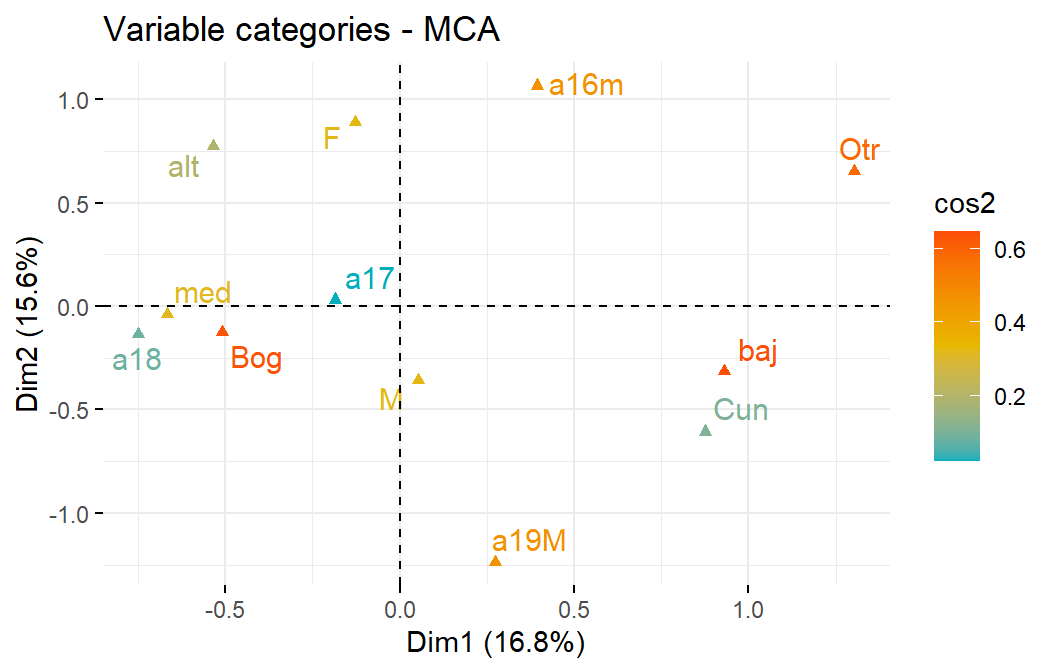
También se calcula la contribución de cada variable, que es la suma de las contribuciones de sus categorías. Además, para una variable cualitativa se puede calcular la razón de correlación con respecto a un eje (los ejes son variables cuantitativas). La razón de correlación en este caso sería la contribución de la variable sobre el eje, multiplicado por el número de variables, multiplicado por el valor propio del eje.
fviz_mca_var(acm, axes = c(1,2),
choice = "mca.cor", repel = TRUE,
ggtheme = theme_minimal())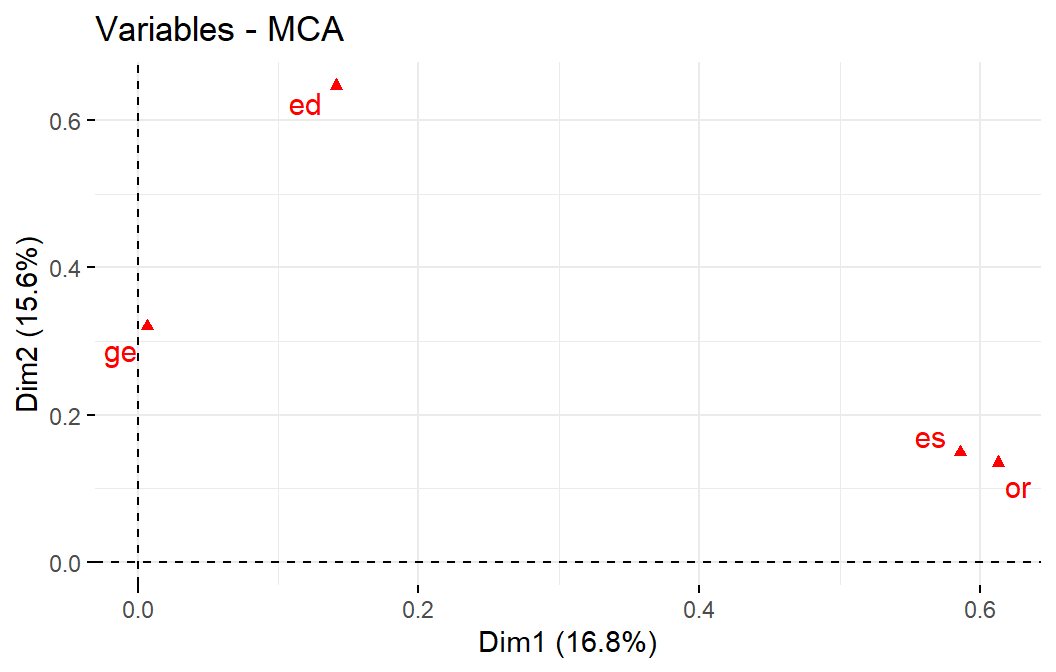
## ¿parece que no está funcionando correctamente?:
# fviz_mca_var(acm, axes = c(3,2),
# choice = "mca.cor", repel = TRUE,
# ggtheme = theme_minimal())
## Haciendo el gráfico sin uso de librerías adicionales:
# plot(acm$var$eta2[,c(3,2)], col="red", pch=17,
# bty="n", xlim = c(0,0.7), ylim = c(0,0.7))
# text(acm$var$eta2[,c(3,2)], col="red", pos = 1,
# labels = rownames(acm$var$eta2))
## Haciendo el gráfico con ggplot:
ggplot(data = acm$var$eta2, aes(x = `Dim 3`, y = `Dim 2`)) +
geom_point(colour = "red") + xlim(0,0.7) + ylim(0,0.7) +
geom_text(label=rownames(acm$var$eta2), colour = "red", hjust=1) +
theme_minimal()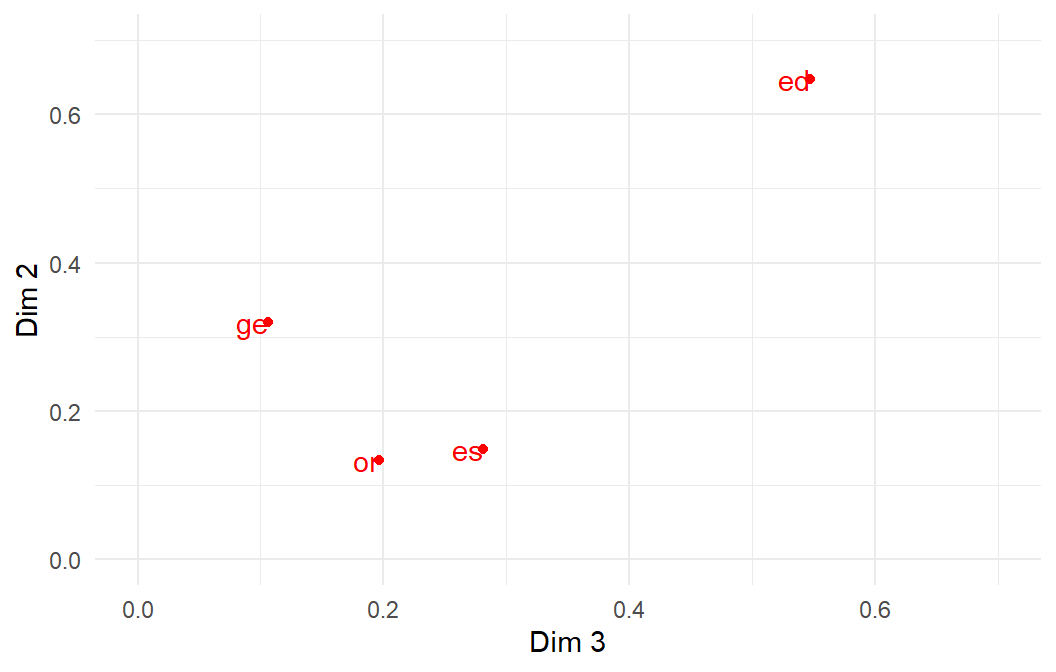
5.7 Elementos ilustrativos o suplementarios
De la misma manera que en ACP y ACS, en el ACM se pueden proyectar individuos, variables cualitativas y variables continuas como elementos ilustrativos.
fviz_mca_var(res.mca, repel = TRUE,
ggtheme= theme_minimal())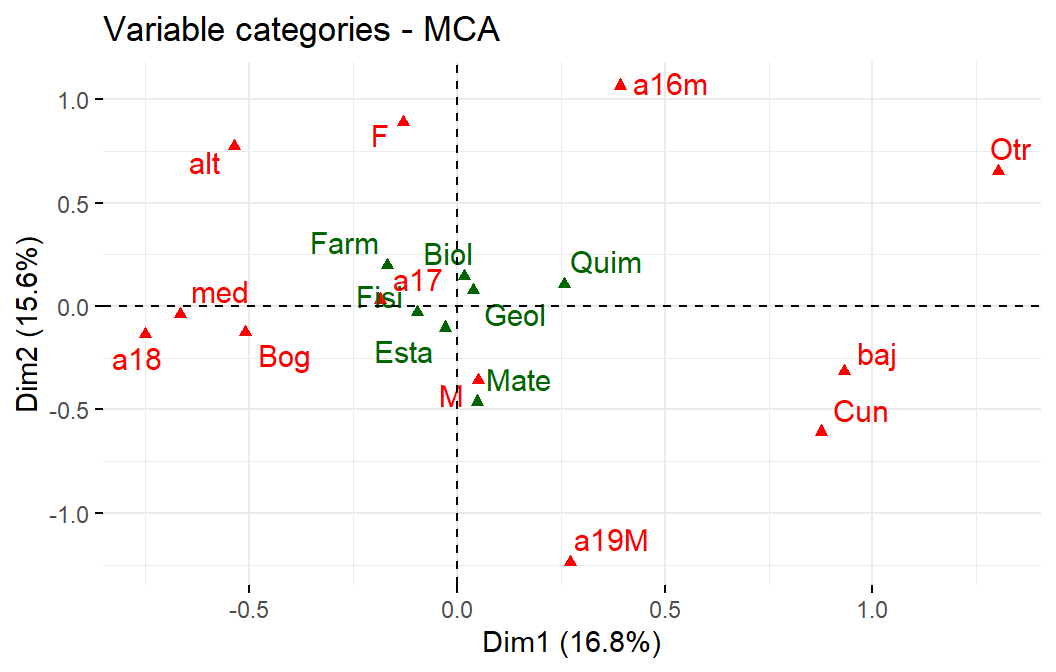
fviz_mca_var(res.mca, axes=c(1,2),
choice="quanti.sup",
ggtheme=theme_minimal())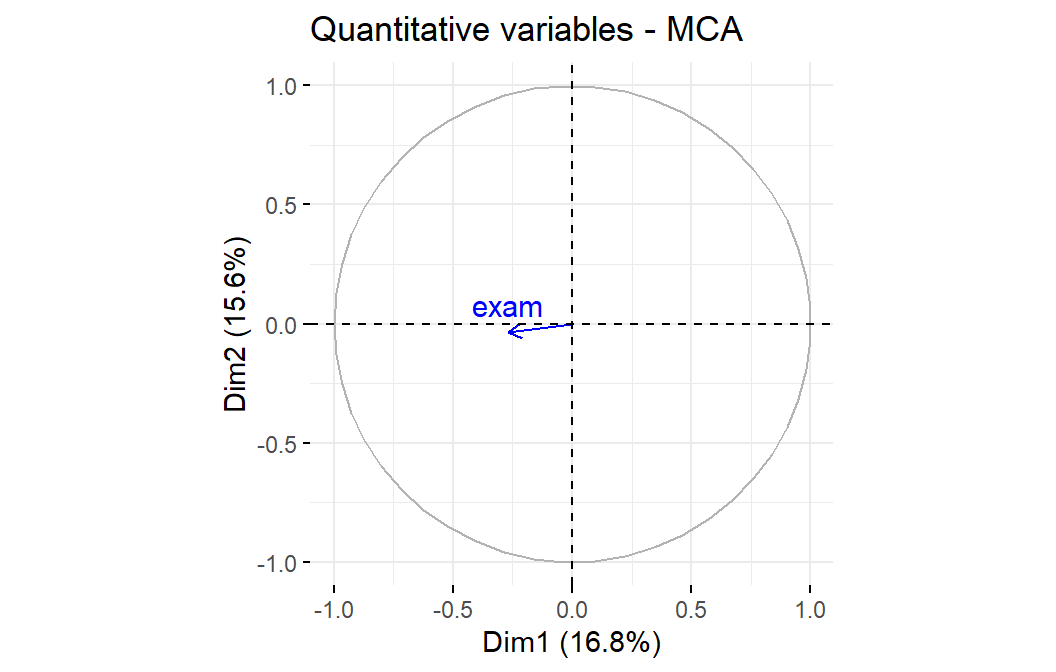
5.8 Otro ejemplo de aplicación del ACM
Consumo cultural (ver la Sección 6.5. del libro guía)
Se presenta un ejemplo de análisis parcial de la Encuesta de Consumo Cultural del Dane (2014). La encuesta aplica un formulario a una subpoblación de niños de 5 a 11 años, sobre consumo cultural. Se adicionan algunas variables sociodemográficas de los módulos de hogares y viviendas. Para este análisis, se seleccionan los niños que tienen edades entre 8 y 11 años y que saben leer.
Objetivos del análisis
Describir el consumo cultural de niños entre 8 y 11 años, que saben leer y explorar su relación con algunas variables sociodemográficas.
# cargar datos de archivo .Rda:
load("./data/ninios8a11.Rda")
# cambia variable a tipo factor
# (también elimina categorías con 0 individuos):
ninios8a11$Edad <- factor(ninios8a11$Edad)
# variables activas: Teat, Libr, Cine, Vide, Radi, Musi
Y <- ninios8a11[, c("Teat","Libr","Cine","Vide","Radi","Musi")]
# variables suplementarias:
Ys <- ninios8a11[, c("Pare","Sexo","Edad","Regi","Estr")]
# ACM con Factoshiny
library(Factoshiny)
res <- MCAshiny(cbind(Y,Ys))