Estadística descriptiva bivariada

Estadística Descriptiva Bivariada (Sección 3 del material de PyEF) https://cjtorresj.quarto.pub/pyef/03-estad_descr_bivar.html

# 4 cifras significativas y sin notación científica:
options(digits = 4, scipen = 999) 
# cargar librerías: 
library(FactoClass)
library(plotly) # para gráficos interactivos
library(knitr) # para función kable (tablas estáticas)
library(DT) # para tablas interactivas
# cargar la tabla ejemplo admitidos:
data(admi) 
n <- nrow(admi) # n: número de individuos

Variables continuas

# Algunas correlaciones
kable(cor(admi[,c(7,15)], admi[,2:6]), digits = 2)

	mate	cien	soci	text	imag
exam	0.75	0.65	0.59	0.52	0.46
age	0.10	-0.02	-0.03	-0.01	0.04

# Diagramas de dispersión y densidades _kernel_
plotpairs(admi[,2:6])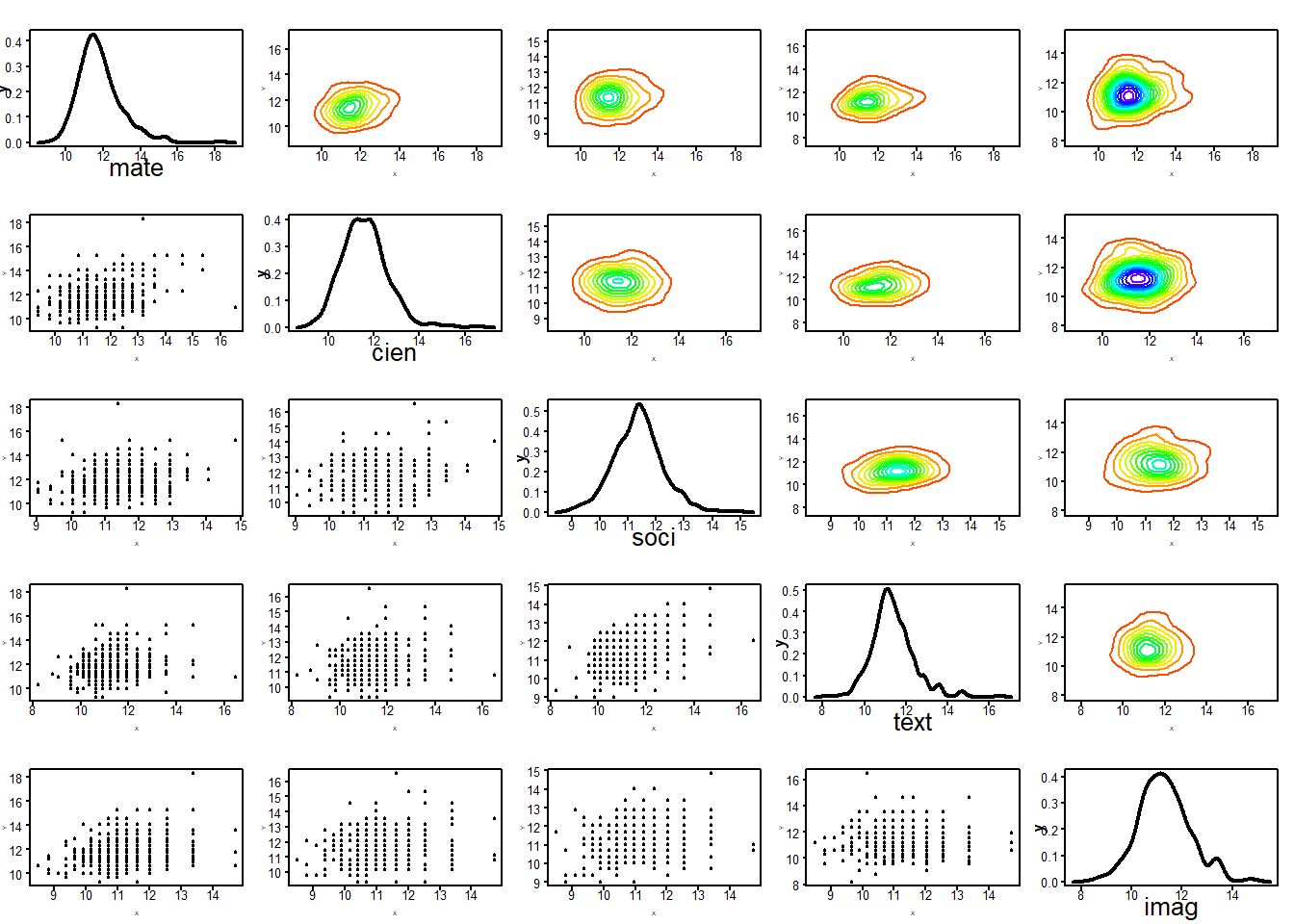

# Matriz de varianzas y covarianzas muestrales
kable(var(admi[,2:6]), digits = 2)

	mate	cien	soci	text	imag
mate	1.28	0.39	0.24	0.27	0.24
cien	0.39	1.00	0.14	0.20	0.12
soci	0.24	0.14	0.75	0.32	0.09
text	0.27	0.20	0.32	0.98	0.05
imag	0.24	0.12	0.09	0.05	1.01

# Matriz de varianzas y covarianzas poblacionales
n <- nrow(admi)
kable(var(admi[, 2:6])*(n-1)/n, digits = 2)

	mate	cien	soci	text	imag
mate	1.28	0.39	0.24	0.27	0.24
cien	0.39	1.00	0.14	0.20	0.12
soci	0.24	0.14	0.75	0.32	0.09
text	0.27	0.20	0.32	0.98	0.05
imag	0.24	0.12	0.09	0.05	1.00

# Matriz de correlaciones
kable(cor(admi[, 2:6]), digits = 2)

	mate	cien	soci	text	imag
mate	1.00	0.34	0.24	0.24	0.21
cien	0.34	1.00	0.16	0.20	0.12
soci	0.24	0.16	1.00	0.37	0.11
text	0.24	0.20	0.37	1.00	0.05
imag	0.21	0.12	0.11	0.05	1.00

Variables continua y cualitativa

# Diagramas de caja _boxplots_
par(bty="n")
sorted_carr <- with(admi, reorder(carr, mate, median, na.rm = T))
boxplot(admi$mate ~ sorted_carr, las = 1, col = 4, horizontal = T)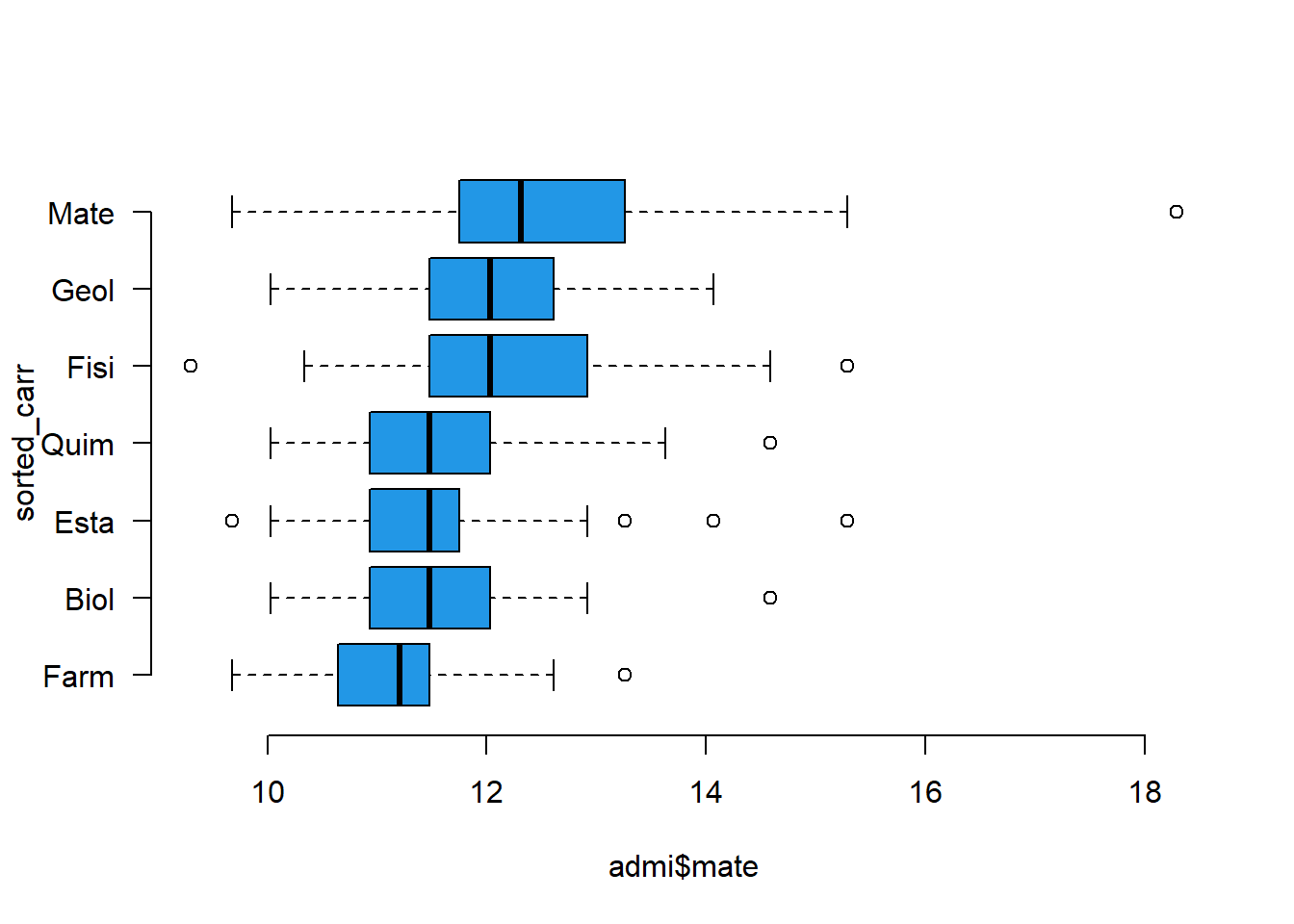

Razón de correlación

\eta^2_{XY} = \frac{\sigma^2_{entre}}{\sigma^2} donde \sigma^2_{entre} = \sum_{k=1}^{K} \frac{n_k}{n} \left( \bar{x}_k - \bar{x}\right)^2

# Gráficos de violín con puntos y media
sorted_carr <- with(admi, reorder(carr, mate, mean, na.rm=T))
fig <- admi %>% plot_ly(x = ~mate, split = sorted_carr, type = 'violin', 
                        points = "all", pointpos = 0,
                        meanline = list(visible = T, color = "black"))
fig <- fig %>% layout(xaxis = list(title = "mate"), 
                      yaxis = list(title = "sorted carr"))

fig

# Razones de correlación (porcentajes)
kable(centroids(admi[, 2:7], admi$carr)$cr*100, digits = 2)

mate	cien	soci	text	imag	exam
15.86	4.31	3.22	2.34	4.42	11.87

Valores test

Sea X con E[X] = \mu y Var[X] = \sigma^2, entonces, para una muestra de tamaño n_k tomada con reemplazamiento (o para una población infinita), se tiene que: E[\bar{X}_k] = \mu y Var\left[\bar{X}_k\right] = \frac{\sigma^2}{n_k}.

Para una muestra sin reemplazamiento de una población finita n, se aplica el factor de corrección: \frac{n - n_k}{n - 1}, entonces, en este caso se tiene que: E[\bar{X}_k] = \mu y Var\left[\bar{X}_k\right] = \frac{n - n_k}{n - 1} \frac{\sigma^2}{n_k}.

Estandarizando el valor \bar{x}_k que tenemos, se obtiene que, \frac{\bar{x}_k - \mu}{\sigma_k} = \sqrt{\frac{(n - 1)n_k}{n - n_k}} \frac{\bar{x}_k - \mu}{\sigma}

Mediante la anterior fórmula podemos obtener valores indicativos, de qué tan lejos está una media \bar{x}_k con respecto a la media general o global, en términos de cantidad de desviaciones estándar \sigma_k, ya sea a la derecha o a la izquierda.

# Valores test para caracterización de carreras
# según los resultados del examen
cluster.carac(admi[,2:7], admi$carr, tipo.v = "co", 
              v.lim = 2, dn = 2, dm = 2, neg = TRUE)

class: Biol
     Test.Value Class.Mean Frequency Global.Mean
mate      -2.26       11.5        63        11.8
------------------------------------------------------------ 
class: Esta
     Test.Value Class.Mean Frequency Global.Mean
text      -2.60      11.06        66       11.36
soci      -2.84      11.08        66       11.36
cien      -3.58      11.18        66       11.59
exam      -3.74     680.21        66      718.35
------------------------------------------------------------ 
class: Farm
     Test.Value Class.Mean Frequency Global.Mean
imag      -2.94      10.98        73        11.3
exam      -3.40     685.74        73       718.4
mate      -4.47      11.25        73        11.8
------------------------------------------------------------ 
class: Fisi
     Test.Value Class.Mean Frequency Global.Mean
mate       3.37      12.18        82       11.80
exam       3.32     748.01        82      718.35
cien       2.48      11.84        82       11.59
------------------------------------------------------------ 
class: Geol
     Test.Value Class.Mean Frequency Global.Mean
exam       2.47     749.61        45       718.4
mate       2.04      12.12        45        11.8
------------------------------------------------------------ 
class: Mate
     Test.Value Class.Mean Frequency Global.Mean
mate       5.82      12.65        53        11.8
exam       3.91     763.53        53       718.4
imag       3.13      11.70        53        11.3
------------------------------------------------------------ 
class: Quim
     Test.Value Class.Mean Frequency Global.Mean
mate       -2.1      11.52        63        11.8

Variables cualitativas

# Tabla de contigencias edad - estrato (frec. abs. y rel.)
tc <- table(admi$edad, admi$estr)
tabtc <- cbind(tc, totF = rowSums(tc))
tabtc <- rbind(tabtc, totC=colSums(tabtc))
kable(cbind(tabtc, rep(" ", 5), round(tabtc/n*100, 1)), 
      digits = 1)

	bajo	medio	alto	totF	bajo	medio	alto	totF
a16m	44	47	27	118	9.9	10.6	6.1	26.5
a17	58	74	39	171	13	16.6	8.8	38.4
a18	22	26	8	56	4.9	5.8	1.8	12.6
a19M	55	38	7	100	12.4	8.5	1.6	22.5
totC	179	185	81	445	40.2	41.6	18.2	100

# Perfiles fila
pf <- prop.table(tc, 1)
kable(rbind(addmargins(pf, margin = 2)*100,
            totC = tabtc[5,]/n*100), digits = 1)

	bajo	medio	alto	Sum
a16m	37.3	39.8	22.9	100
a17	33.9	43.3	22.8	100
a18	39.3	46.4	14.3	100
a19M	55.0	38.0	7.0	100
totC	40.2	41.6	18.2	100

# Perfiles columna
pc <- prop.table(tc, 2)
kable(cbind(addmargins(pc, margin = 1)*100,
            totF = tabtc[,4]/n*100), digits = 1)

	bajo	medio	alto	totF
a16m	24.6	25.4	33.3	26.5
a17	32.4	40.0	48.1	38.4
a18	12.3	14.1	9.9	12.6
a19M	30.7	20.5	8.6	22.5
Sum	100.0	100.0	100.0	100.0

# Gráficos de los perfiles fila y perfiles columna
par(mfrow=c(2,1), mai=c(0.4,1,0.3,0.1))
plotct(t(tc), "row", col=2:5)
plotct(tc, "row", col=2:4)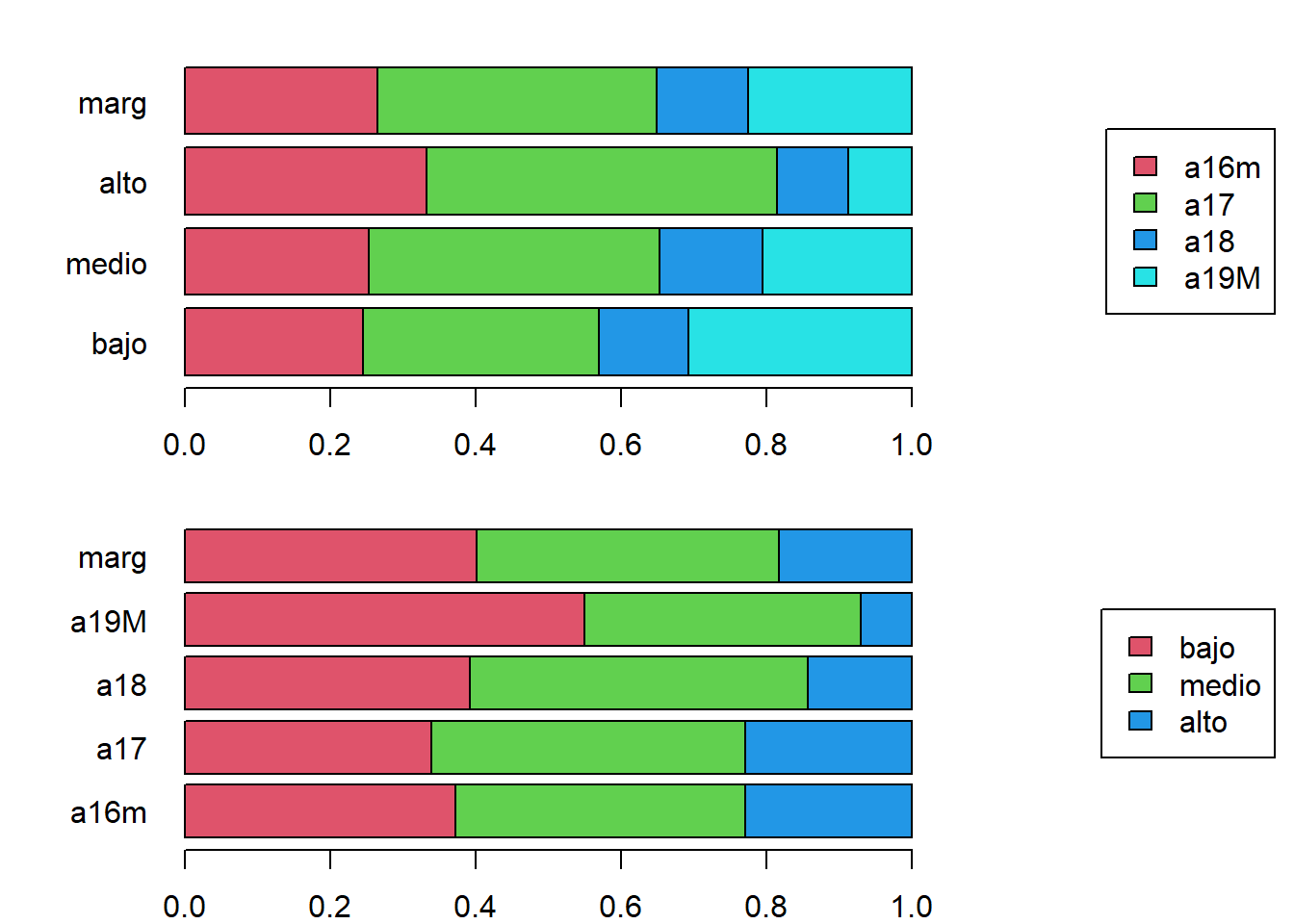

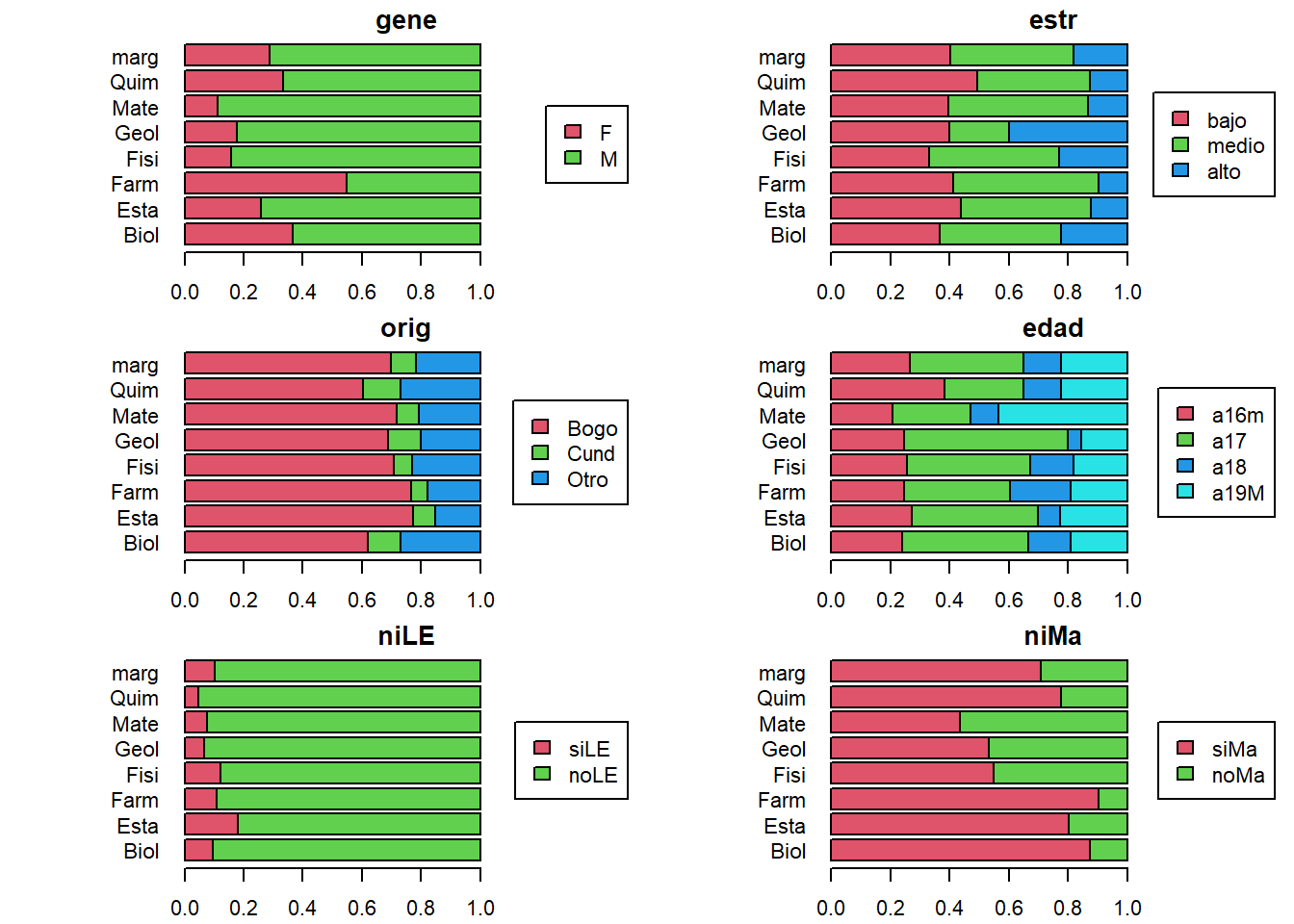
# Gráficos de perfiles de las carreras según cada cualitativa
par(mfrow = c(3,2), mai = c(0.3,1,0.2,0.1), las = 1, cex = 0.7)
for(i in 8:13){
  tc <- unclass(table(admi$carr, admi[,i]))
  plotct(tc, "row", col=1+(1:ncol(tc)))
  title(main = names(admi)[i])
}

Medida de asociación

\chi^2 = \sum_{j=1}^J \sum_{k=1}^K \frac{\left(n_{jk}-\dfrac{n_{j\cdot} n_{\cdot k}}{n} \right)^2}{\dfrac{n_{j\cdot} n_{\cdot k}}{n} }

\phi^2 = \frac{\chi^2}{n}

# Valores indicativos de asociación
kable(chisq.carac(admi[,8:11], admi$carr, decr = FALSE), digits=3)

	chi2	dfr	pval	tval	phi2
gene	44.108	6	0.000	5.264	0.099
estr	29.190	12	0.004	2.679	0.066
orig	9.676	12	0.644	-0.370	0.022
edad	33.553	18	0.014	2.189	0.075

Valores test

# Además de graficar, la función plotct devuelve 
# tabla de contingencia y tablas de perfiles
tcCarrNiMa <- unclass(table(admi$niMa, admi$carr))
tabs <- plotct(tcCarrNiMa, tables = TRUE)

# Tabla perfiles fila
kable(tabs$perR, digits = 1)

	Biol	Esta	Farm	Fisi	Geol	Mate	Quim
siMa	17.5	16.8	21.0	14.3	7.6	7.3	15.6
noMa	6.2	10.0	5.4	28.5	16.2	23.1	10.8
marg	14.2	14.8	16.4	18.4	10.1	11.9	14.2

# Tabla perfiles columna
kable(tabs$perC, digits = 1)

	Biol	Esta	Farm	Fisi	Geol	Mate	Quim	marg
siMa	87.3	80.3	90.4	54.9	53.3	43.4	77.8	70.8
noMa	12.7	19.7	9.6	45.1	46.7	56.6	22.2	29.2

# Tabla de contingencia (frec. rel.)
kable(tabs$ctm/n*100, digits = 1)

	Biol	Esta	Farm	Fisi	Geol	Mate	Quim	marR
siMa	12.4	11.9	14.8	10.1	5.4	5.2	11.0	70.8
noMa	1.8	2.9	1.6	8.3	4.7	6.7	3.1	29.2
marC	14.2	14.8	16.4	18.4	10.1	11.9	14.2	100.0

# Tabla de contingencia (frec. abs.)
kable(tabs$ctm, digits = 0)

	Biol	Esta	Farm	Fisi	Geol	Mate	Quim	marR
siMa	55	53	66	45	24	23	49	315
noMa	8	13	7	37	21	30	14	130
marC	63	66	73	82	45	53	63	445

# Valor test para Biología (k=1) y "siMa" (j=1)
# De n = 445, n_j = 315 tienen la característica "siMa"
# Al tomar una muestra sin reemplazamiento de n_k = 63
# ¿cuál es la probabilidad de que hayan salido n_kj = 55
# o algo "peor" (más alejado de la independencia)?
# valor p = P[ X >= 55 ] donde X ~ Hg(N = 445, M = 315, n = 63)
# P[ X >= 55 ] = 1 - P[ X <= 54 ]
(vp <- 1 - phyper(54, 315, 445-315, 63))

[1] 0.0008624

# P[ X >= 55 ] = P[ X > 54 ]
(vp <- phyper(54, 315, 445-315, 63, lower.tail = FALSE))

[1] 0.0008624

# Cuantil de la normal asociado a ese valor p (dos colas)
(t <- qnorm(vp/2, lower.tail = FALSE))

[1] 3.332

# Representación gráfica del cuantil (valor test) obtenido
plot(c(-5,5), c(-0.03, 0.4), type = "n", bty = "n", 
     axes = F, xlab = "", ylab = "")
abline(v = seq(-5,5), h = seq(0, 0.4, 0.1), col = "gray")
abline(v = c(-t,t), lty = 2, col = "red") # cuantiles
axis(1, pos=0)
axis(2, pos=0, las=1)
curve(dnorm(x), add = T, las = 1, col = "blue")
text(t, 0, signif(vp/2,2), adj = c(0,1), cex = 0.7, col = "blue")
text(t, -0.03, round(t,3), col = "red", cex = 0.9)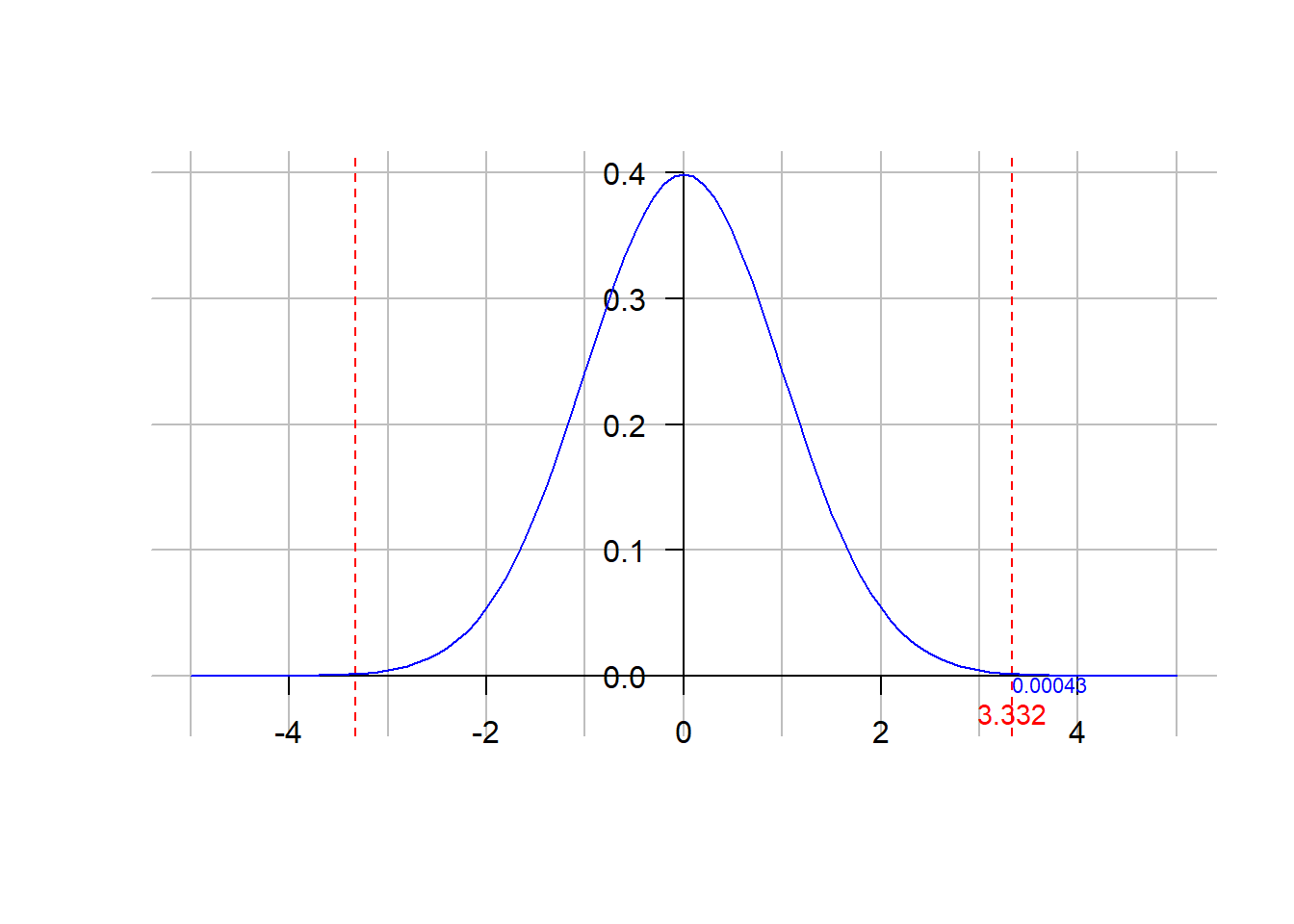

# Valores test para caracterización de carreras
# según las variables cualitativas
cluster.carac(admi[,8:13], admi[,1])

class: Biol
          Test.Value p.Value Class.Cat Cat.Class Global Weight
niMa.siMa      3.332   0.001      17.5      87.3   70.8    315
niMa.noMa     -3.332   0.001       6.2      12.7   29.2    130
------------------------------------------------------------ 
class: Esta
          Test.Value p.Value Class.Cat Cat.Class Global Weight
niLE.siLE      2.235   0.025      26.1      18.2   10.3     46
niMa.siMa      2.034   0.042      16.8      80.3   70.8    315
niMa.noMa     -2.034   0.042      10.0      19.7   29.2    130
niLE.noLE     -2.235   0.025      13.5      81.8   89.7    399
------------------------------------------------------------ 
class: Farm
          Test.Value p.Value Class.Cat Cat.Class Global Weight
gene.F         5.152   0.000      31.2      54.8   28.8    128
niMa.siMa      4.355   0.000      21.0      90.4   70.8    315
edad.a18       2.252   0.024      26.8      20.5   12.6     56
estr.alto     -2.281   0.023       8.6       9.6   18.2     81
niMa.noMa     -4.355   0.000       5.4       9.6   29.2    130
gene.M        -5.152   0.000      10.4      45.2   71.2    317
------------------------------------------------------------ 
class: Fisi
          Test.Value p.Value Class.Cat Cat.Class Global Weight
niMa.noMa      3.475   0.001      28.5      45.1   29.2    130
gene.M         3.045   0.002      21.8      84.1   71.2    317
gene.F        -3.045   0.002      10.2      15.9   28.8    128
niMa.siMa     -3.475   0.001      14.3      54.9   70.8    315
------------------------------------------------------------ 
class: Geol
           Test.Value p.Value Class.Cat Cat.Class Global Weight
estr.alto       3.677   0.000      22.2      40.0   18.2     81
niMa.noMa       2.706   0.007      16.2      46.7   29.2    130
edad.a17        2.554   0.011      14.6      55.6   38.4    171
niMa.siMa      -2.706   0.007       7.6      53.3   70.8    315
estr.medio     -3.242   0.001       4.9      20.0   41.6    185
------------------------------------------------------------ 
class: Mate
          Test.Value p.Value Class.Cat Cat.Class Global Weight
niMa.noMa      4.467   0.000      23.1      56.6   29.2    130
edad.a19M      3.683   0.000      23.0      43.4   22.5    100
gene.M         3.218   0.001      14.8      88.7   71.2    317
edad.a17      -2.089   0.037       8.2      26.4   38.4    171
gene.F        -3.218   0.001       4.7      11.3   28.8    128
niMa.siMa     -4.467   0.000       7.3      43.4   70.8    315
------------------------------------------------------------ 
class: Quim
          Test.Value p.Value Class.Cat Cat.Class Global Weight
edad.a16m      2.320   0.020      20.3      38.1   26.5    118
edad.a17      -2.189   0.029       9.9      27.0   38.4    171

Taller (razas de perros)

Caracterización de la función de razas de perros

data(DogBreeds) # cargar datos
# Tabla dinámica con función datatable {DT}:
datatable(DogBreeds, style = "bootstrap4",
          options = list(pageLength = 5))

summary(DogBreeds) # Resumen

  SIZE     WEIG     SPEE     INTE     AFFE     AGGR     FUNC   
 lar:15   hea: 5   hig: 9   hig: 6   hig:14   hig:13   com:10  
 med: 5   lig: 8   low:10   low: 8   low:13   low:14   hun: 9  
 sma: 7   med:14   med: 8   med:13                     uti: 8

# chisq.carac (valores indicativos de asociación)
kable(chisq.carac(DogBreeds[,1:6], DogBreeds[,7], 
                  decr = FALSE),
      digits=3)

	chi2	dfr	pval	tval	phi2
SIZE	16.354	4	0.003	2.797	0.606
WEIG	24.407	4	0.000	3.822	0.904
SPEE	8.483	4	0.075	1.437	0.314
INTE	4.140	4	0.387	0.286	0.153
AFFE	14.761	2	0.001	3.228	0.547
AGGR	7.073	2	0.029	1.894	0.262

# cluster.carac (valores test)
cluster.carac(DogBreeds[,1:6], DogBreeds[,7], dn = 2, dm = 2)

class: com
         Test.Value p.Value Class.Cat Cat.Class Global Weight
AFFE.hig       3.85       0      71.4       100   51.9     14
WEIG.lig       3.31       0      87.5        70   29.6      8
SIZE.sma       2.87       0      85.7        60   25.9      7
SIZE.lar      -3.54       0       6.7        10   55.6     15
AFFE.low      -3.85       0       0.0         0   48.1     13
------------------------------------------------------------ 
class: hun
         Test.Value p.Value Class.Cat Cat.Class Global Weight
WEIG.med       2.62    0.01      57.1      88.9   51.9     14
AFFE.low       2.08    0.04      53.8      77.8   48.1     13
AFFE.hig      -2.08    0.04      14.3      22.2   51.9     14
------------------------------------------------------------ 
class: uti
         Test.Value p.Value Class.Cat Cat.Class Global Weight
WEIG.hea       3.39    0.00     100.0      62.5   18.5      5
SIZE.lar       2.98    0.00      53.3     100.0   55.6     15
AGGR.hig       2.53    0.01      53.8      87.5   48.1     13
WEIG.lig      -2.12    0.03       0.0       0.0   29.6      8
SPEE.med      -2.12    0.03       0.0       0.0   29.6      8
AGGR.low      -2.53    0.01       7.1      12.5   51.9     14