4  ACS

Código a ejecutar antes de empezar:

# 4 cifras significativas y sin notación científica:
options(digits = 4, scipen = 999) 
# cargar librerías: 
library(FactoClass)
library(factoextra)
library(knitr) # para función kable (tablas estáticas)
library(DT) # para tablas interactivas
library(plotly) # para gráficos interactivos

El análisis de correspondencias simples (ACS) se puede realizar sobre tablas de contingencia (TC), tablas de frecuencias, y algunas tablas de números positivos para las que tenga sentido el análisis.

Un ejemplo, de una tabla de números positivos de interés que se podría describir mediante el ACS, es una tabla del producto interno bruto (PIB) agrupado según departamentos y subsectores de la economía. La suma de las filas es la distribución del PIB por departamentos y la de las columnas la distribución del PIB por subsectores de la economía. El total de la tabla es el PIB del país.

4.1 Ejemplo de “juguete” (admitidos)

Recordemos que una tabla de contingencia (TC) es una tabla de resumen de dos variables cualitativas, las filas son categorías de una variable y las columnas son las categorías de la otra. En una celda se encuentra el número de objetos que asumen simultáneamente la categoría de la fila y la de la columna correspondientes. La suma de una fila, o de una columna, es el total de objetos que tiene la categoría respectiva.

Tabla de frecuencias absolutas (edad y carrera):

library(FactoClass)
data(admi) # carga datos admi de FactoClass
K <- unclass(table(admi$edad, admi$carr))
K_add <- addmargins(K)
Biol Esta Farm Fisi Geol Mate Quim Sum
a16m 15 18 18 21 11 11 24 118
a17 27 28 26 34 25 14 17 171
a18 9 5 15 12 2 5 8 56
a19M 12 15 14 15 7 23 14 100
Sum 63 66 73 82 45 53 63 445

Tabla de frecuencias relativas en porcentaje:

k <- sum(K)
F_add <- K_add / k
Biol Esta Farm Fisi Geol Mate Quim Sum
a16m 3.4 4.0 4.0 4.7 2.5 2.5 5.4 26.5
a17 6.1 6.3 5.8 7.6 5.6 3.1 3.8 38.4
a18 2.0 1.1 3.4 2.7 0.4 1.1 1.8 12.6
a19M 2.7 3.4 3.1 3.4 1.6 5.2 3.1 22.5
Sum 14.2 14.8 16.4 18.4 10.1 11.9 14.2 100.0

Los totales de las filas (las sumas horizontales) se denominan marginal fila, y los totales de las columnas (las sumas verticales), marginal columna.

Tablas de perfiles:

Código
# ver ayuda de la función plotct de FactoClass
tabs <- plotct(K, tables = TRUE)

Tabla de perfiles fila en porcentaje (tabs$perR):

Biol Esta Farm Fisi Geol Mate Quim
a16m 12.7 15.3 15.3 17.8 9.3 9.3 20.3
a17 15.8 16.4 15.2 19.9 14.6 8.2 9.9
a18 16.1 8.9 26.8 21.4 3.6 8.9 14.3
a19M 12.0 15.0 14.0 15.0 7.0 23.0 14.0
marg 14.2 14.8 16.4 18.4 10.1 11.9 14.2

Recuerden que los perfiles fila corresponden a unas probabilidades condicionales entre las categorías de una variable con respecto a las categorías de la otra.

Tabla de perfiles columna en porcentaje (tabs$perC):

Biol Esta Farm Fisi Geol Mate Quim marg
a16m 23.8 27.3 24.7 25.6 24.4 20.8 38.1 26.5
a17 42.9 42.4 35.6 41.5 55.6 26.4 27.0 38.4
a18 14.3 7.6 20.5 14.6 4.4 9.4 12.7 12.6
a19M 19.0 22.7 19.2 18.3 15.6 43.4 22.2 22.5

Recuerden que los perfiles columna corresponden a las otras probabilidades condicionales que se pueden tener entre categorías.

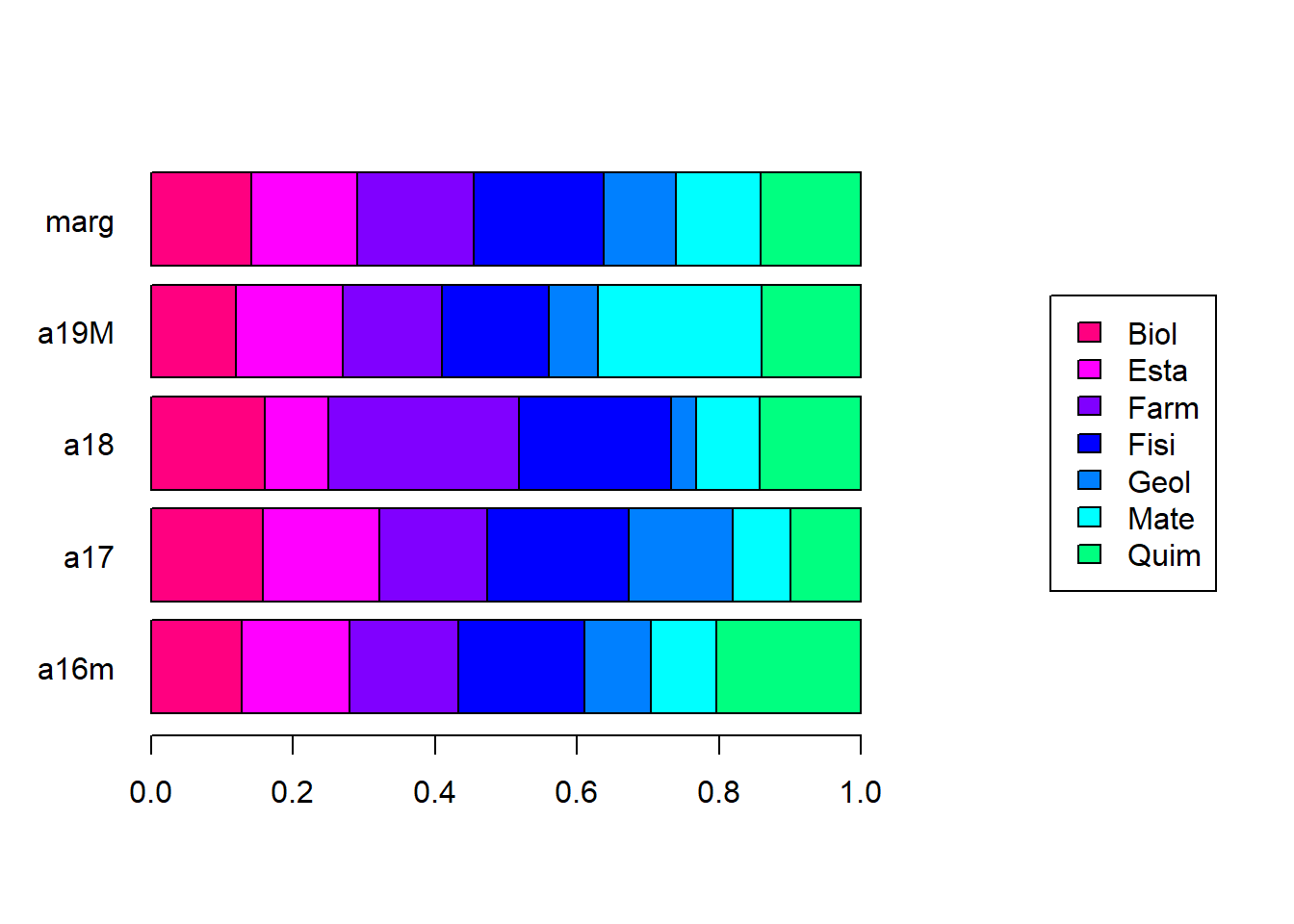
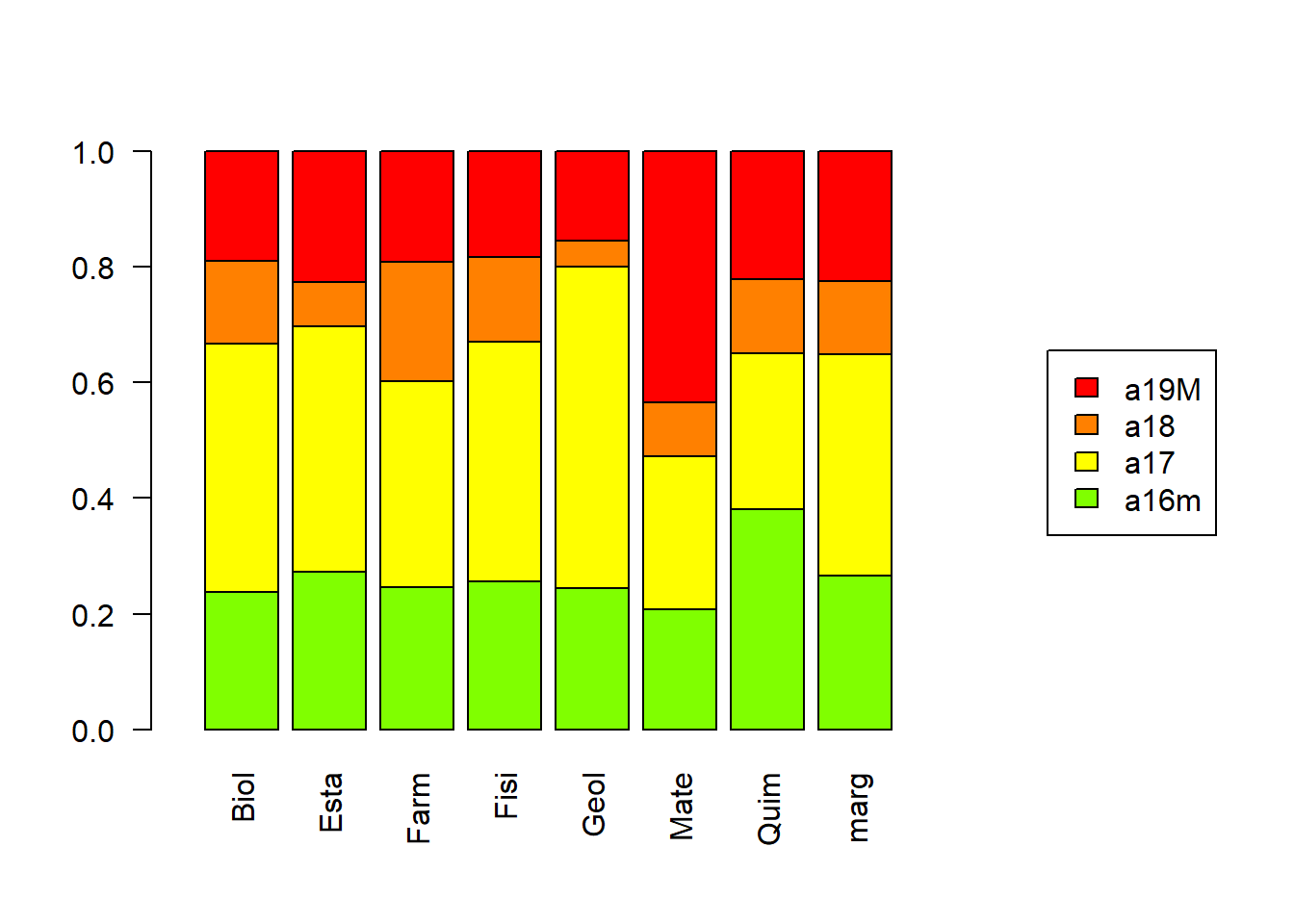
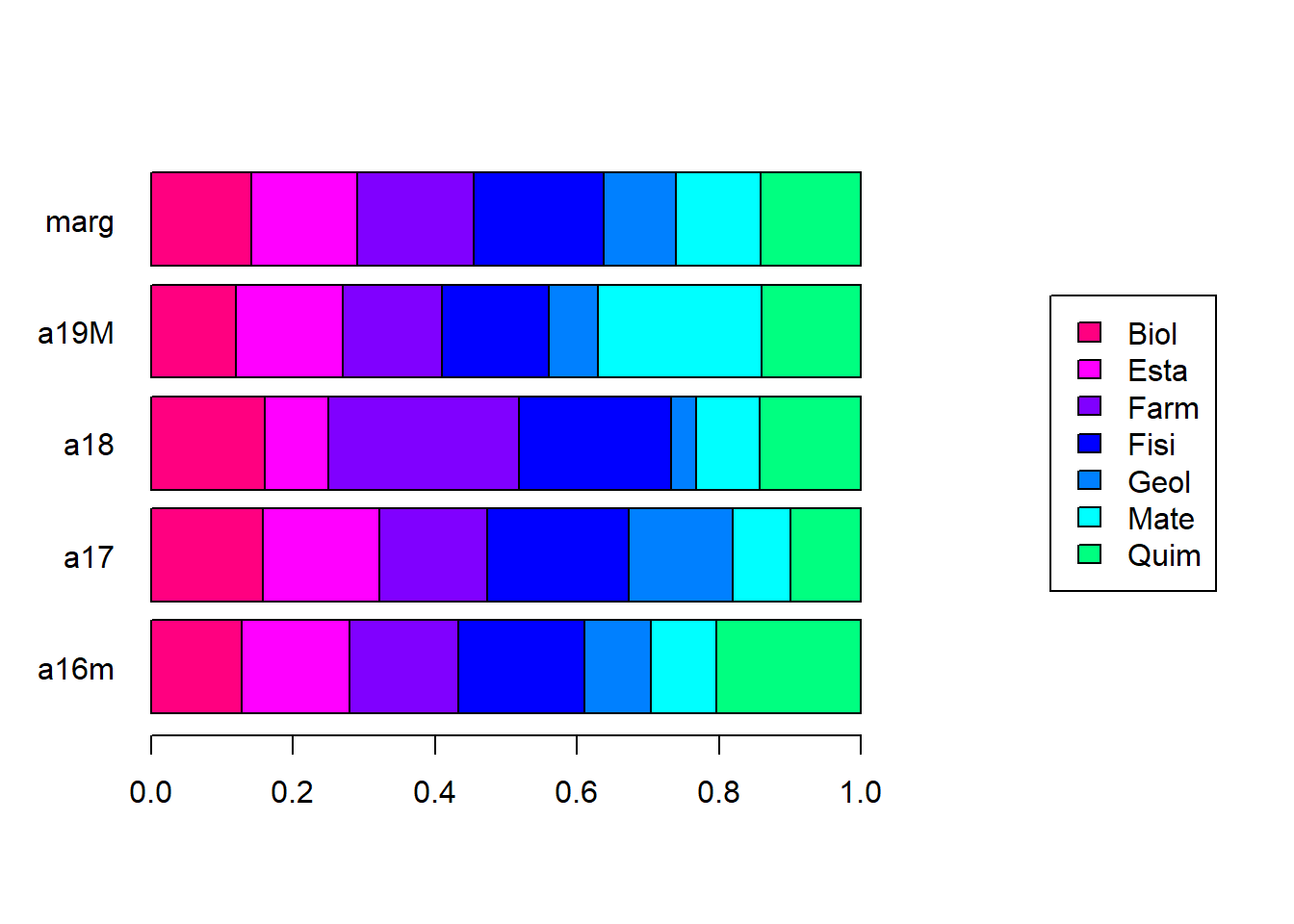
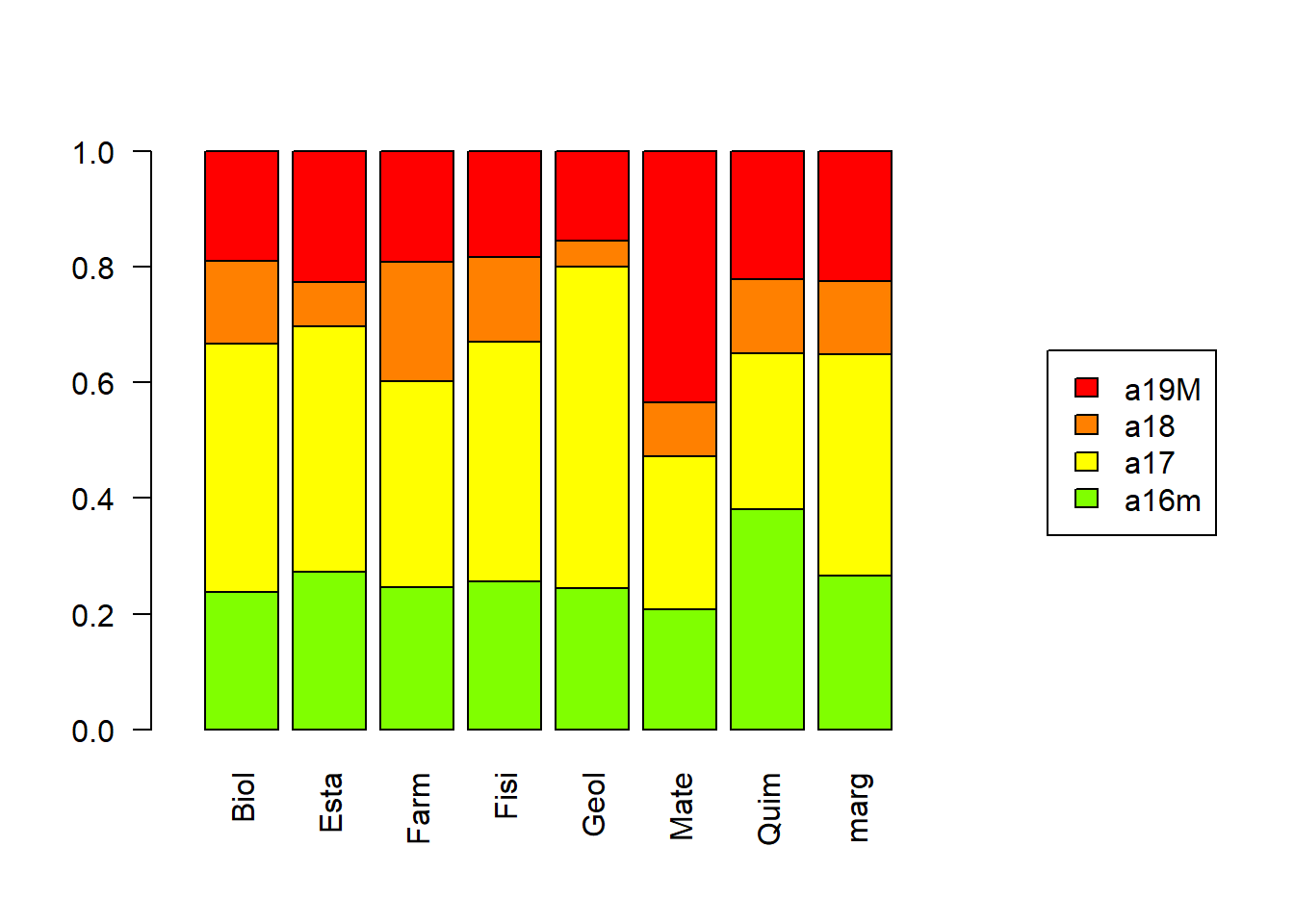
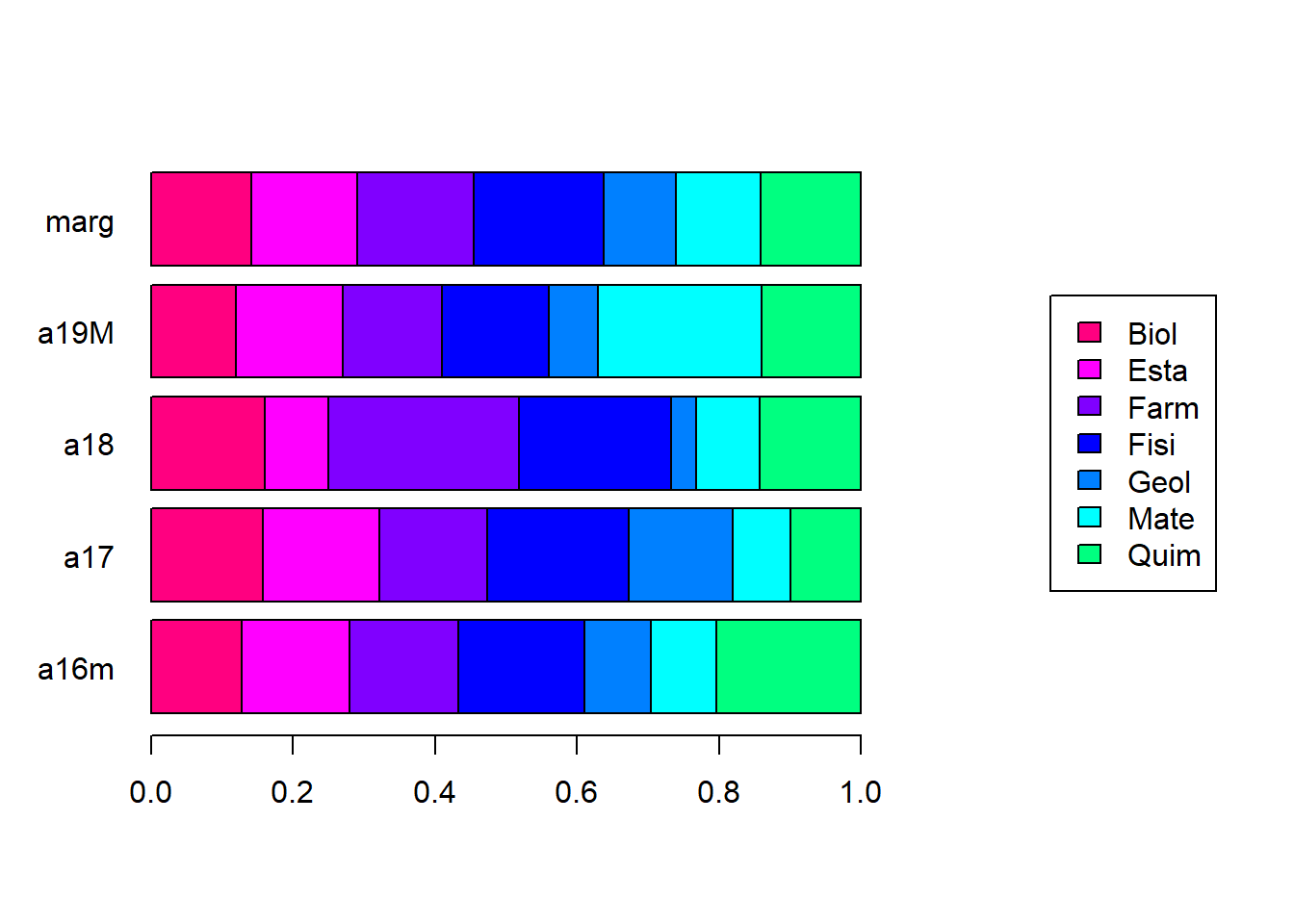
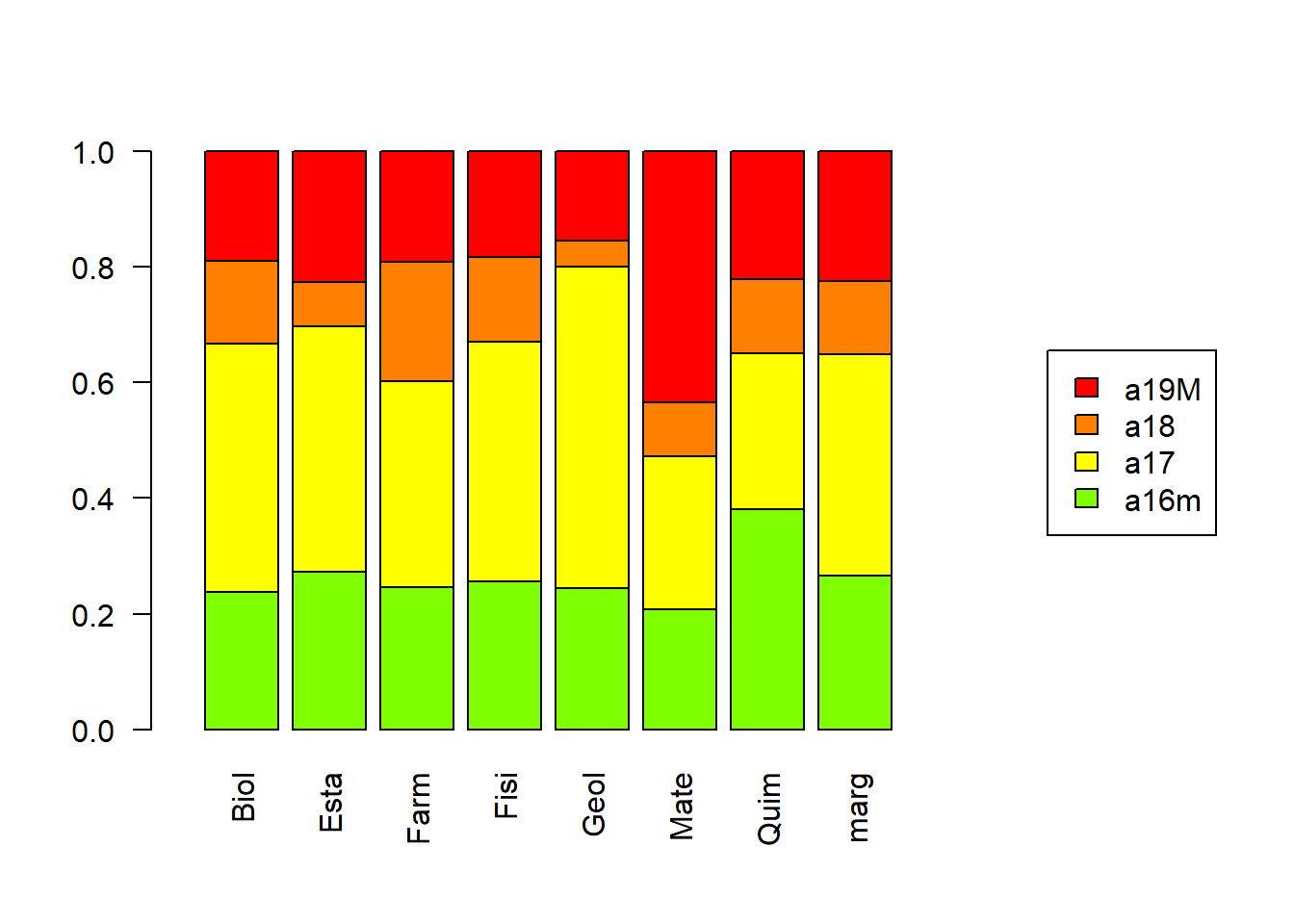
Representación gráfica de las tablas de perfiles:

Código
colores <- rainbow(12, rev = TRUE)
plotct(K, "row", col = colores[1:7])

Código
colores <- rainbow(12, rev = TRUE)
plotct(K, "col", col = colores[9:12])

Si todas las categorías de una variable fueran estadísticamente independientes de todas las categorías de la otra variable, los perfiles fila y columna deberían ser iguales a las marginales, y los gráficos deberían verse así:

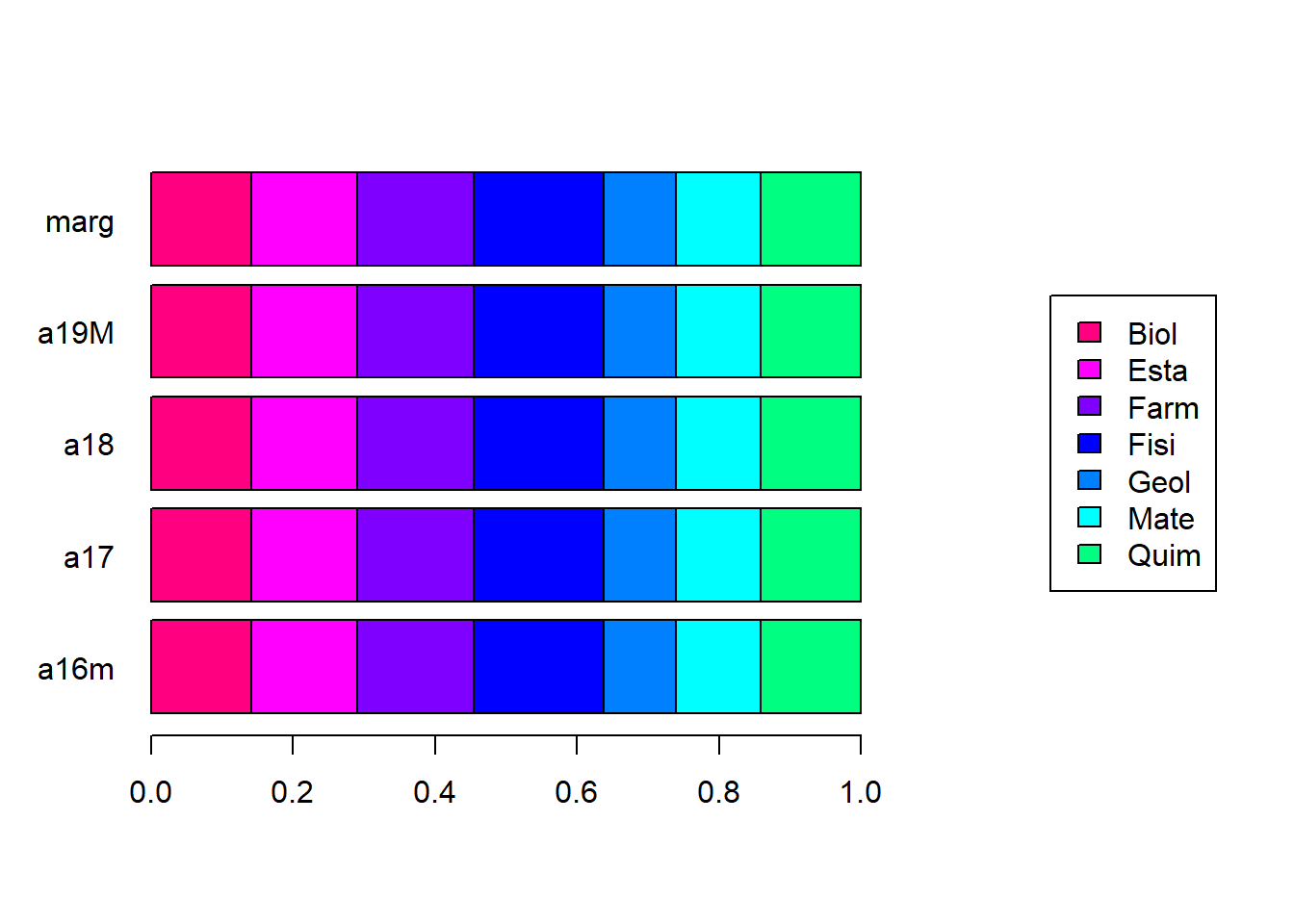
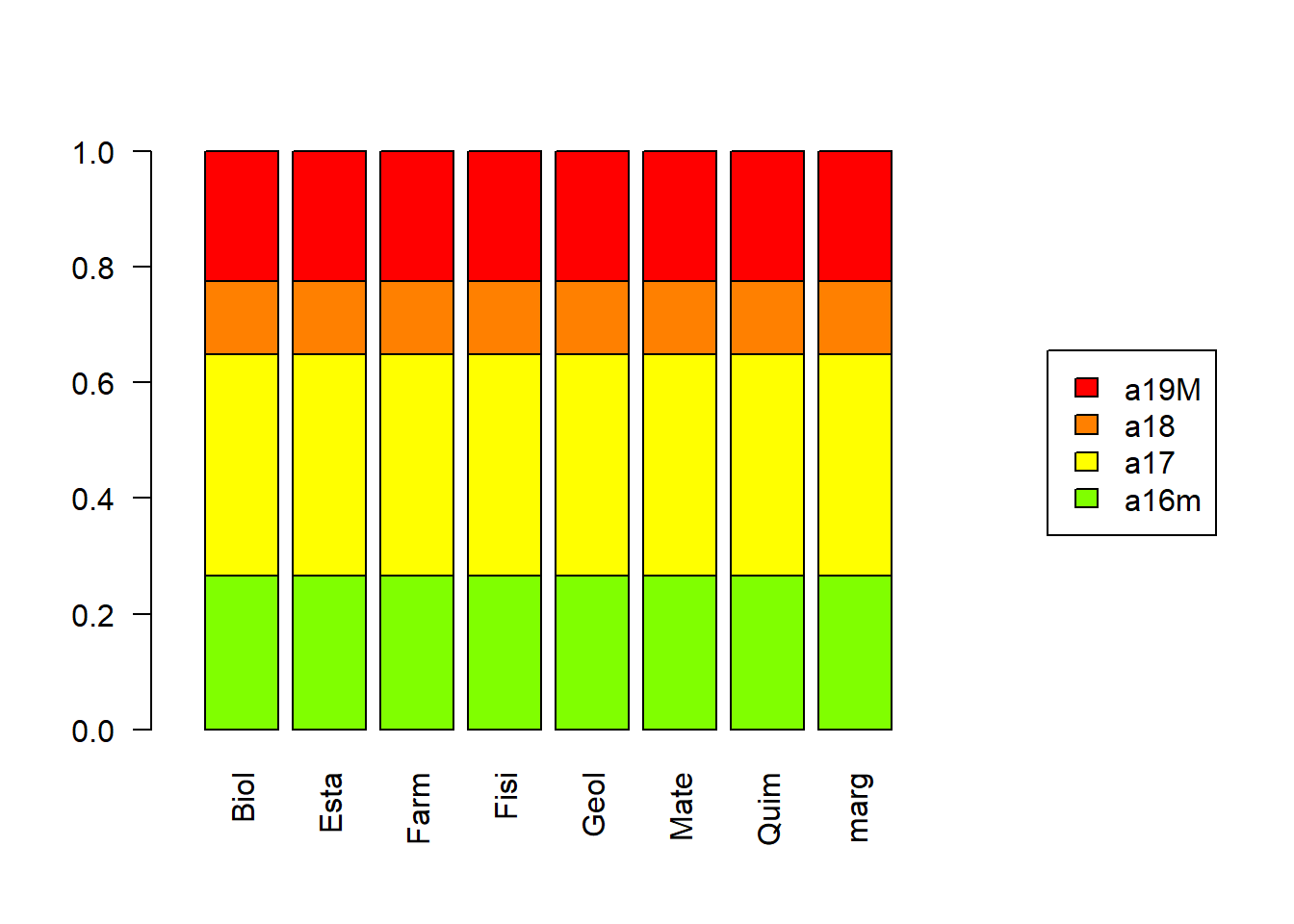
Por otro lado, si todas las categorías de una variable fueran independientes de todas las categorías de la otra variable, cada celda de la tabla de frecuencias relativas debería ser igual al producto de las marginales fila y columna respectivas.

Tabla de frecuencias relativas, esperadas bajo independencia, en porcentaje:

Biol Esta Farm Fisi Geol Mate Quim Sum
a16m 3.8 3.9 4.3 4.9 2.7 3.2 3.8 26.5
a17 5.4 5.7 6.3 7.1 3.9 4.6 5.4 38.4
a18 1.8 1.9 2.1 2.3 1.3 1.5 1.8 12.6
a19M 3.2 3.3 3.7 4.1 2.3 2.7 3.2 22.5
Sum 14.2 14.8 16.4 18.4 10.1 11.9 14.2 100.0

Tabla de diferencias (desvíos), entre las frecuencias relativas observadas y las esperadas bajo independencia, en puntos porcentuales:

Biol Esta Farm Fisi Geol Mate Quim
a16m -0.38 0.11 -0.31 -0.17 -0.21 -0.69 1.64
a17 0.63 0.59 -0.46 0.56 1.73 -1.43 -1.62
a18 0.24 -0.74 1.31 0.38 -0.82 -0.38 0.02
a19M -0.48 0.04 -0.54 -0.77 -0.70 2.49 -0.04

El ACS va más allá de la denominada prueba (de hipótesis) de independencia que se suele hacer para las tablas de contingencia, ya que permite describir las dependencias entre categorías fila y columna, al comparar perfiles fila y columna obtenidos a partir de la tabla de datos de interés.

4.2 Características del ACS

El ACS nos permite:

  • Comparar los perfiles fila.
  • Comparar los perfiles columna.
  • Estudiar las correspondencias entre perfiles fila y columna.

El ACS también se puede usar para:

  • Reducir la dimensión.
  • Separar información de “ruido”.
  • Asociar valores numéricos a las categorías fila y columna (cuantificar).

El ACS se puede ver como:

  • Dos ACP, uno de los perfiles fila y otro de perfiles columna, que se superponen.
  • Un ACP de las diferencias (los desvíos) entre las frecuencias relativas observadas y las esperadas bajo independencia.

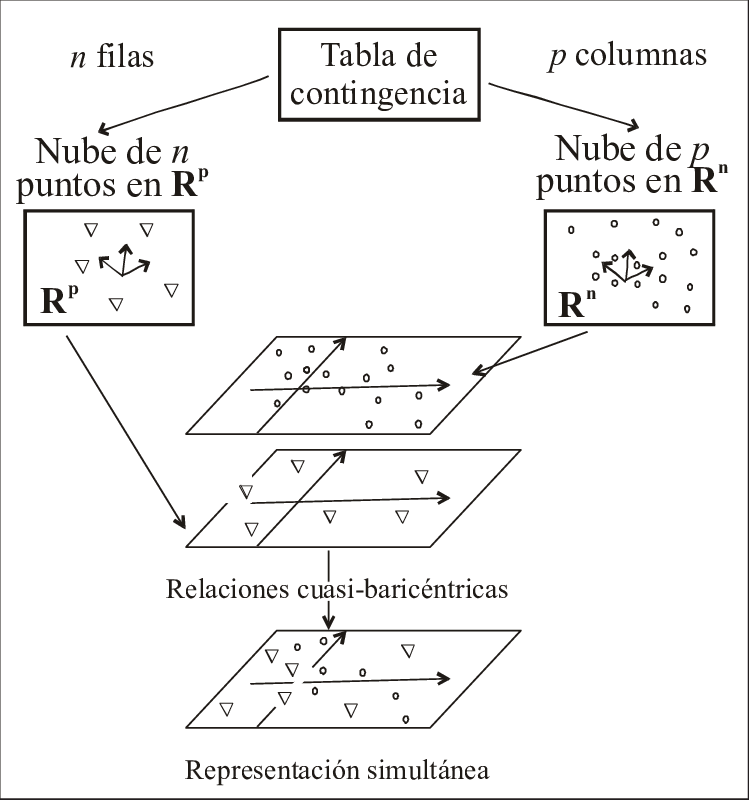
4.3 El ACS como dos ACP generalizados

Para cada tabla de perfiles se realiza un ACP generalizado, pero como los dos ACP están relacionados, esto permite representaciones simultaneas de los planos factoriales resultantes de los dos ACP.

Sea F la matriz de frecuencias relativas, D_n la matriz diagonal con los valores marginales fila y D_p la matriz diagonal con los valores marginales columna.

El ACP generalizado de los perfiles fila es:

ACP\left(X = D_{n}^{-1}F \, , \, M = D_{p}^{-1} \, , \, N = D_{n}\right)

El ACP generalizado de los perfiles columna es:

ACP\left(X = D_{p}^{-1}F' \, , \, M = D_{n}^{-1} \, , \, N = D_{p}\right)

4.3.1 ACP perfiles fila

Código
# OPCIÓN 1 (ade4 + FactoClass):
library(FactoClass) # cargar FactoClass
acs <- dudi.coa(K, scannf=FALSE, nf=3)
Código
# OPCIÓN 2 (FactoMineR + Factoshiny):
library(Factoshiny) # cargar Factoshiny
K <- as.data.frame(K) # cambia a tipo dataframe
res <- CAshiny(K) # activar ACS para K

Primer plano factorial de los perfiles fila (edades):

Código
plot(acs, ex=1, ey=2, Tcol=FALSE, 
     asp=1, cframe=1, gg=TRUE)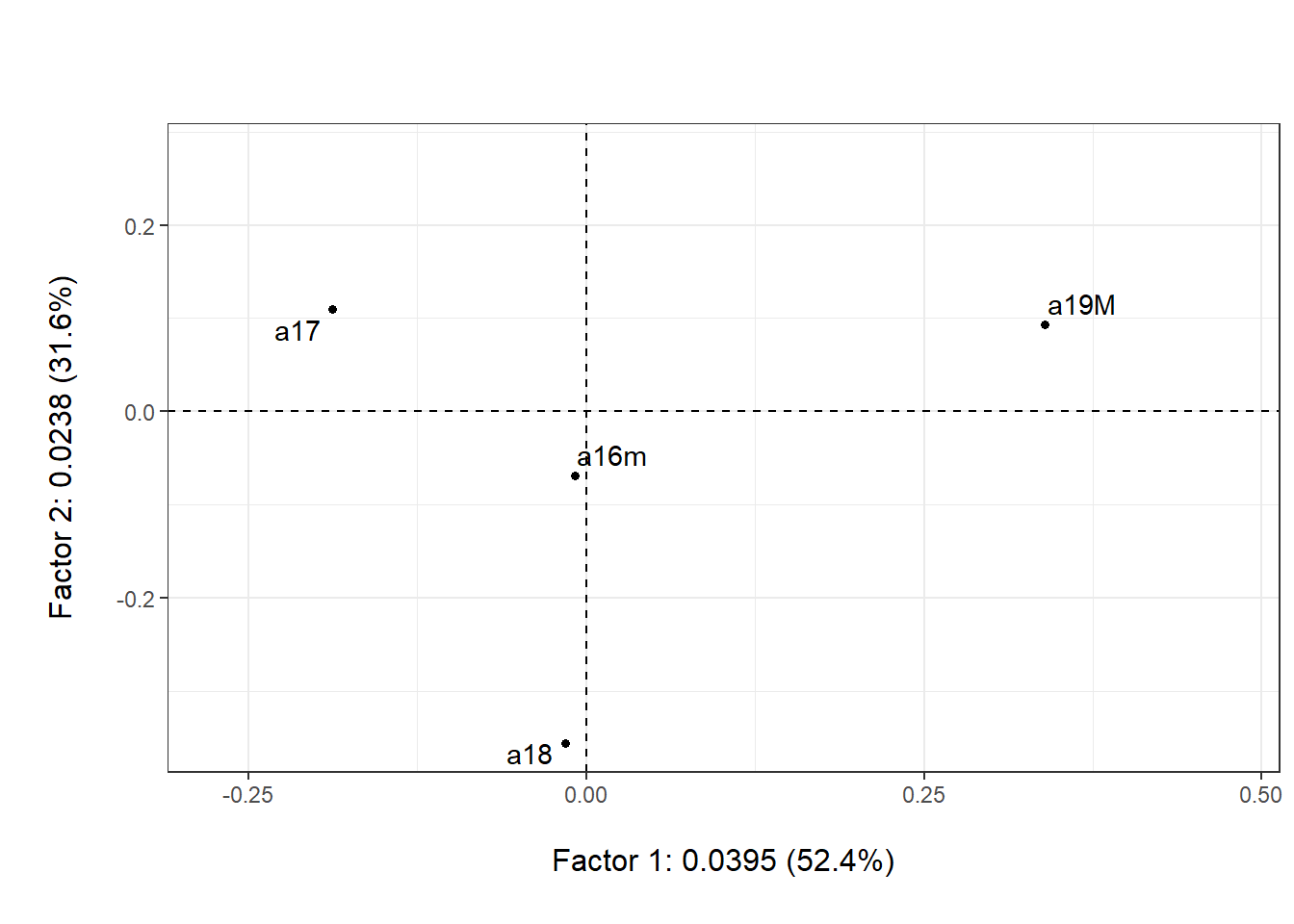

Código
colores <- rainbow(12, rev = TRUE)
plotct(K, "row", col = colores[1:7])

Como el ACP generalizado de los perfiles fila es ACP\left(X = D_{n}^{-1}F \, , \, M = D_{p}^{-1} \, , \, N = D_{n}\right), entonces:

  • Las coordenadas de los puntos son las filas de la tabla X = D_{n}^{-1} F \left(x_{ij} = \tfrac{f_{ij}}{f_{i\cdot}}\right), es decir que cada perfil fila (diagrama de barras de cada fila) se representa por un punto en \mathbb{R}^p.

  • Los pesos de los puntos fila son los valores de la marginal de filas \left(f_{i \cdot}\right) (valores de la suma horizontal de la tabla de frecuencias relativas).

  • El centro de gravedad es la distribución marginal columna (suma vertical)

  • La diferencia entre dos perfiles (dos diagramas de barras) es la distancia entre los puntos en \mathbb{R}^p, dada por la matriz D_{p}^{-1} (distancia ji cuadrado o de Benzécri). Se amplifican las diferencias entre coordenadas, cuando se deben a columnas de baja frecuencia marginal.

  • La inercia coincide con el valor del estadístico de una prueba de independencia (\chi^2) dividido por el total de individuos (k) (índice de asociación \phi^2).

4.3.2 ACP perfiles columna

Primer plano factorial de los perfiles columna (carreras):

Código
plot(acs, ex=1, ey=2, Trow=FALSE, 
     asp=1, cframe=1, gg=TRUE)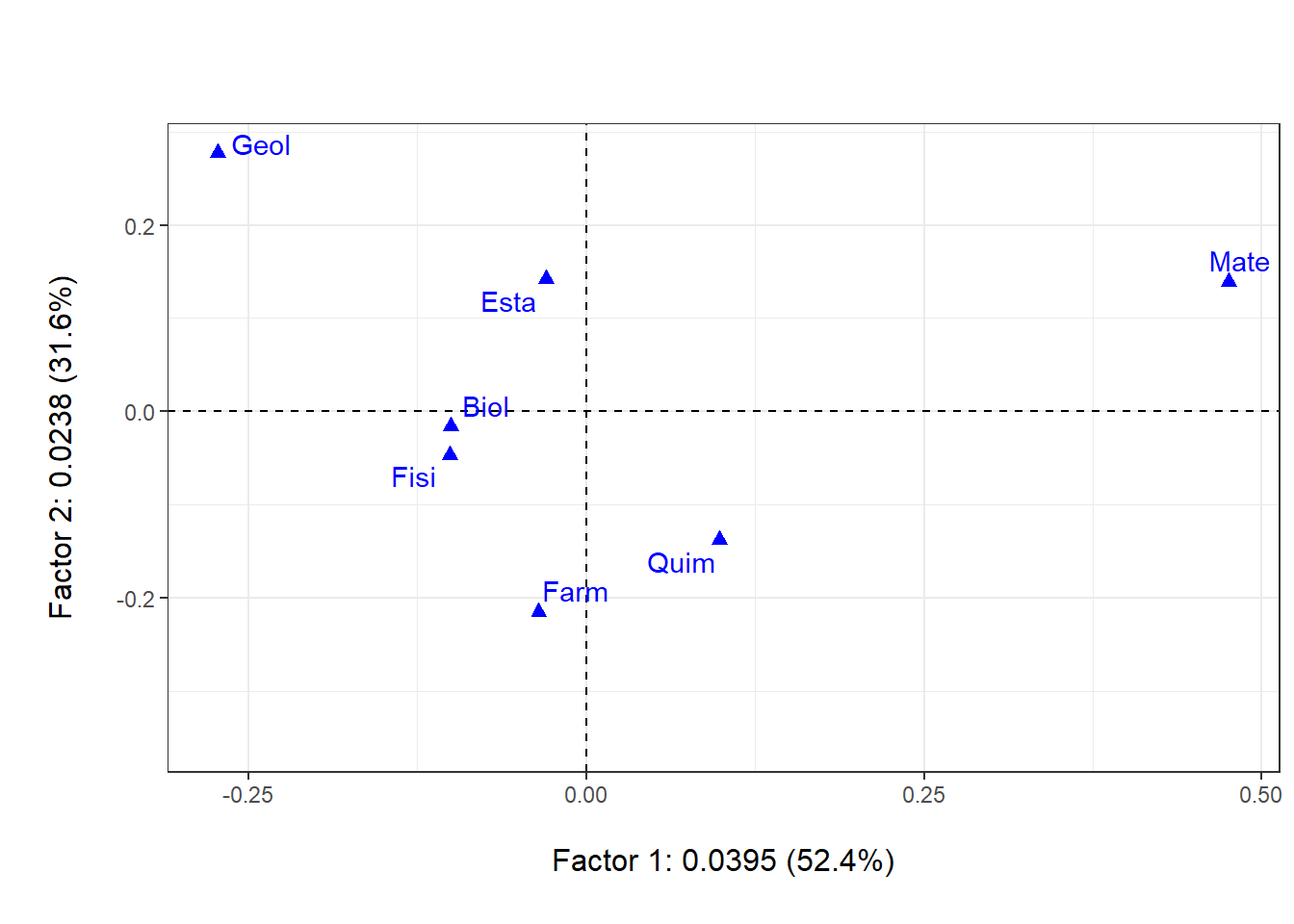

Código
colores <- rainbow(12, rev = TRUE)
plotct(K, "col", col = colores[9:12])

Las características del análisis para los perfiles columna son similares (“simétricos”) a los ya mencionados para los perfiles filas.

4.4 El ACS como un ACP generalizado de los desvios

El ACS de la tabla de frecuencias relativas también se puede obtener mediante el ACP generalizado de los desvíos (con respecto a lo esperado bajo independencia):

ACP\left(X = D_{n}^{-1}FD_{p}^{-1} \, , \, M = D_{p} \, , \, N = D_{n}\right)

  • Las coordenadas de los puntos son las frecuencias observadas menos las frecuencias esperadas, dividido por las esperadas,

    x_{ij} = \tfrac{ f_{ij} - f_{ i \cdot } f_{ \cdot j } }{ f_{ i \cdot } f_{ \cdot j } } = \tfrac{ f_{ij} }{ f_{ i \cdot } f_{ \cdot j } } - 1

Visto de una forma o de la otra, la distancia ji cuadrado le confiere al ACS dos propiedades:

  • Las relaciones cuasi-baricéntricas (que son las que permiten la representación simultánea de perfiles fila y columna).
  • La equivalencia distribucional.

4.4.1 Representación simultánea de perfiles fila y columna

Código
plot(acs, ex=1, ey=2, asp=1, cframe=1, gg=TRUE)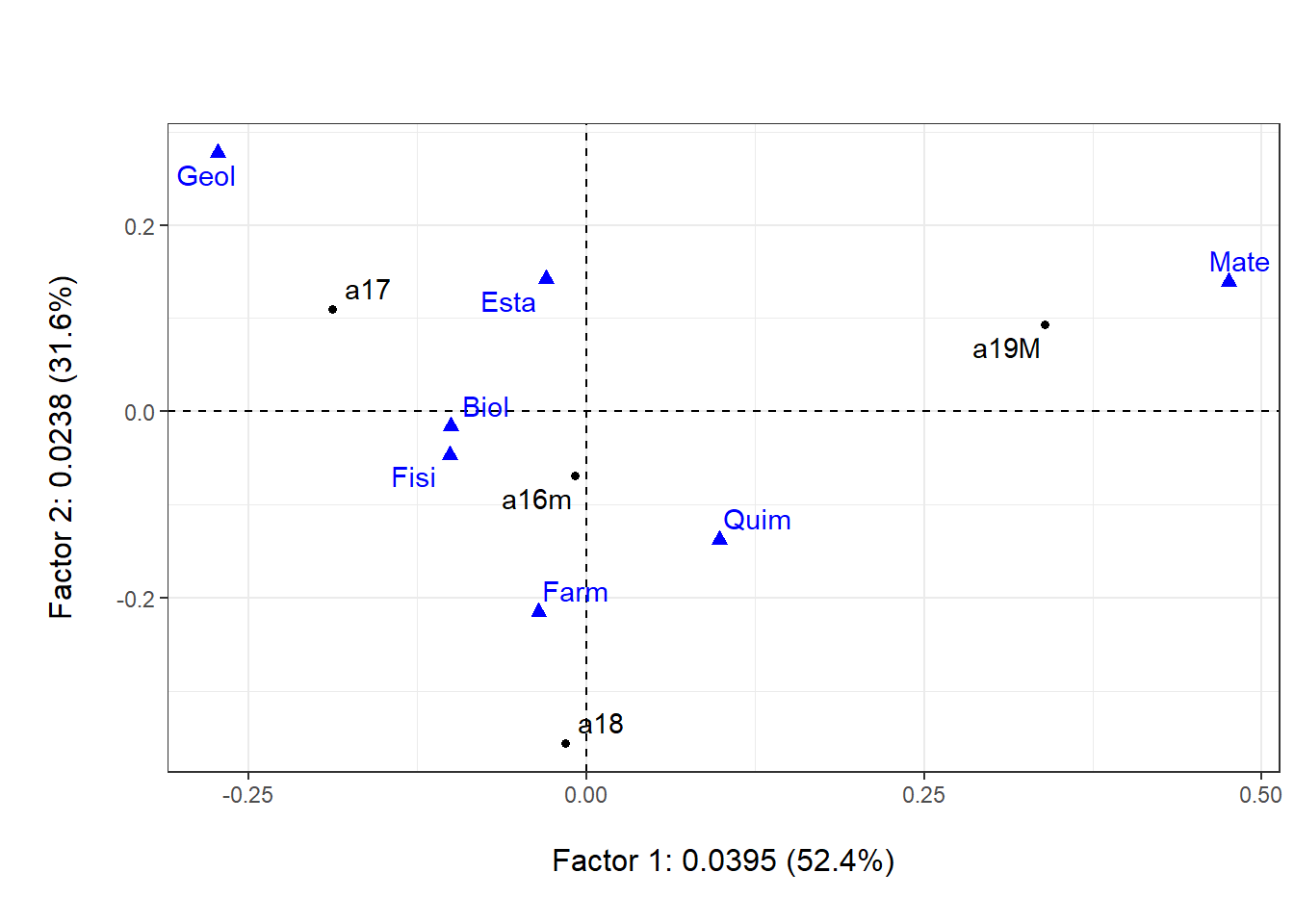

4.4.2 Relaciones cuasibaricéntricas

  • Una coordenada de una fila se puede dar en función de las coordenadas de las columnas. Una coordenada de una columna se puede dar en función de las coordenadas de las filas.

    F_s(i) = \tfrac{1}{\sqrt{\lambda_s}}\sum_{j=1}^p{\tfrac{f_{ij}}{f_{i\cdot}} G_s(j)} \quad \text{y} \quad G_s(j) = \tfrac{1}{\sqrt{\lambda_s}}\sum_{i=1}^n{{\tfrac{f_{ij}}{f_{\cdot j}} F_s(i)}}

  • Las sumatorias son promedios ponderados, lo que las hace ser centros de gravedad o baricentros. La multiplicación por \tfrac{1}{\sqrt{\lambda_s}} dilata, es decir, aleja la coordenada del baricentro. Por eso se denominan relaciones cuasibaricéntricas.

  • Las relaciones cuasibaricéntricas hacen posible la representación simultánea y su interpretación como una doble atracción o un doble “jalonamiento” entre las coordenadas de los perfiles fila y los de los perfiles columna.

  • La dilatación hace que la asociación más destacada sea también la más alejada.

4.4.3 Equivalencia distribucional

  • El ACS no se modifica si se unen dos puntos que tienen el mismo perfil. El peso del punto colapsado es la suma de los pesos de los puntos que se unen.

  • Lo anterior permite unir filas o columnas con perfiles parecidos, para simplificar las tablas originales.

  • Esta propiedad hace que el ACS sea “robusto” ante la “arbitrariedad” en la conformación de las categorías de una variable.

En el caso de ACS, también tendremos las respectivas ayudas numéricas para la interpretación (inercia, valores propios, coordenadas, contribuciones y cosenos cuadrados), y elementos ilustrativos o suplementarios (filas, columnas u otras variables que no participan en la obtención de los ejes del análisis).

4.5 Otros ejemplos de aplicación del ACS

4.5.1 Resultados de los exámenes de Estado de la educación básica en Colombia según departamentos

El objetivo principal del análisis es comparar los perfiles departamentales según la calidad educativa de los colegios. También se desea explorar la influencia de la jornada sobre el ordenamiento de los departamentos y la influencia de su tamaño, en términos de población, en ese ordenamiento. (Ver la ayuda de los datos ?icfes08 y la Sección 5.4. del libro guía)

Código
library(Factoshiny) # cargar Factoshiny
data("icfes08") # cargar datos 
res <- CAshiny(icfes08) # ACS

4.5.2 Adjetivos × colores

Una agencia de publicidad encarga un estudio sobre las asociaciones entre colores y adjetivos, para armonizar la publicidad de los productos con las imágenes que los compradores potenciales tienen de los colores (Ver la ayuda de los datos ?ColorAdjective y el taller de la Subsección 5.6.2. del libro guía).

Código
library(Factoshiny) # cargar Factoshiny
data("ColorAdjective") # cargar datos 
res <- CAshiny(ColorAdjective) # ACS