# cambia idioma de la consola de R a español:
Sys.setenv(LANG="es")
# usar 2 cifras significativas y tiende a evitar
# notación científica (ver ayuda de función: `options`):
options(digits = 2, scipen = 999)
# cargar librerías:
if(!require(FactoClass)){
install.packages("FactoClass"); library(FactoClass)}
if(!require(Factoshiny)){
install.packages("Factoshiny"); library(Factoshiny)}
if(!require(factoextra)){
install.packages("factoextra"); library(factoextra)}
if(!require(plotly)){
install.packages("plotly"); library(plotly)} # gráficos dinámicos6 Agrupamiento
Ver Capítulo 7 de: Pardo, C. (2020). Estadística descriptiva multivariada. https://repositorio.unal.edu.co/handle/unal/79914
Código a ejecutar antes de empezar:
6.1 Introducción
El objetivo de los métodos de agrupamiento es descubrir patrones en los datos, en forma de grupos bien diferenciados, que tengan individuos homogéneos en su interior.
En las áreas de minería de datos, aprendizaje automático y reconocimiento de patrones, estos métodos hacen parte de lo que se denominaría como aprendizaje no supervisado (unsupervised learning).
En la literatura francesa de análisis de datos (d’analyse des données) se los denomina métodos de clasificación (techniques de classification), mencionando que son no supervisados (non supervisé) cuando se necesita la aclaración. Por otro lado, Partitionnement de données, en francés, sería un término similar o equivalente a data clustering en inglés.
Los métodos de agrupamiento se pueden dividir inicialmente en dos categorías principales:
Agrupamiento estricto (hard): en este enfoque, cada elemento se asigna de forma clara y definitiva a un solo grupo o se considera fuera de cualquier grupo.
Agrupamiento difuso (soft, fuzzy): en este caso, cada elemento puede estar asociado a múltiples grupos, con diferentes grados de pertenencia, como una probabilidad de que forme parte de cada uno.
En el sentido matemático, un algoritmo de agrupamiento estricto buscaría una partición de un conjunto de elementos (los individuos) en subconjuntos (grupos). Esto es equivalente a asignarle una categoría a cada individuo (una etiqueta que indica el subconjunto o grupo al que pertenece), y por lo tanto es como obtener una nueva variable cualitativa a partir de los datos.
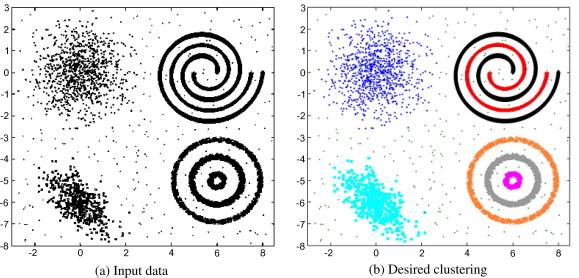
Existen una gran cantidad de métodos de agrupamiento, y diferentes tipos de ellos, con sus respectivas ventajas y desventajas. En esta sección nos concentraremos, primero, en un método que obtiene los grupos a partir de una sucesión de particiones (agrupamiento jerárquico), y luego, en un método que obtiene los grupos a partir de la cantidad de grupos deseados, unos puntos iniciales y un criterio de parada (agrupamiento directo).
6.2 Medidas de similitud, disimilitud o distancia
Los algoritmos de agrupamiento suelen necesitar medidas de similitud, disimilitud o distancia entre individuos y entre grupos.
Las medidas de similitud evalúan el grado de parecido o proximidad existente entre dos elementos. Los valores más altos indican mayor parecido o proximidad entre los elementos comparados.
Las medidas de disimilitud ponen el énfasis en el grado de diferencia o lejanía existente entre dos elementos. Los más altos indican mayor diferencia o lejanía entre los elementos comparados.
Si la medida de disimilitud cumple la propiedad 1, se denomina índice de distancia; si verifica la propiedad 2, se llama desviación; si cumple la 1 y 2, se llama distancia y si cumple las propiedades 1 y 3 (la propiedad 3 implica la 2), se llama ultra-métrica:
- d(i,l) = 0 implica que i = l.
- d(i,l) \leq d(i,k) + d(l,k) para todo i, j, k.
- d(i,l) \leq \max \{d(i,k) \, , \, d(l,k)\} para todo i, j, k.
Existen varias medidas de similitud, disimilitud y distancia entre individuos, dependiendo del tipo de variable y del contexto de aplicación.
6.2.1 Algunas distancias entre individuos para variables continuas
Distancia euclidiana:
\begin{aligned} d(i, l) = d(\vec{x}_i,\vec{x}_l) &= \sqrt{( x_{i1} - x_{l1} )^2 + \dots + ( x_{ip} - x_{lp} )^2} \end{aligned}
Distancia Manhattan o Cityblock:
\begin{aligned} d(i, l) = d(\vec{x}_i,\vec{x}_l) &= | x_{i1} - x_{l1} | + \dots + | x_{ip} - x_{lp} | \end{aligned}
Distancia del máximo o de Chebyschev:
\begin{aligned} d(i, l) = d(\vec{x}_i,\vec{x}_l) &= \max \{ |x_{i1} - x_{l1}| , \dots , |x_{ip} - x_{lp}| \} \end{aligned}
6.3 Agrupamiento jerárquico
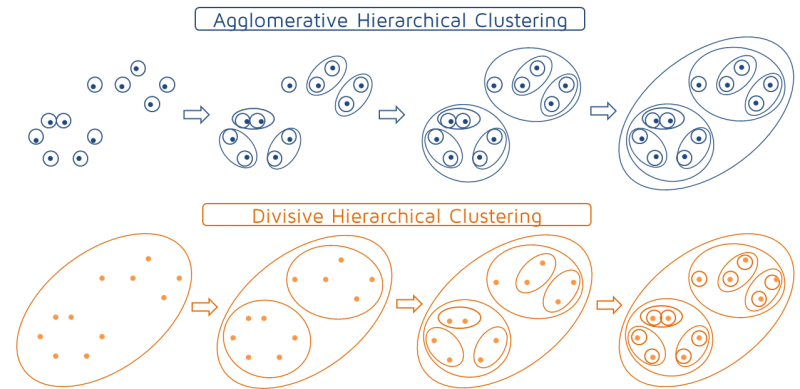
6.3.1 Agrupamiento jerárquico aglomerativo
Un procedimiento de agrupamiento jerárquico aglomerativo procede de la siguiente manera:
- Seleccionar una medida de disimilitud (o distancia) entre individuos, y seleccionar un criterio de agregación o medida de disimilitud (o distancia) entre grupos.
- Calcular las disimilitudes (o distancias) entre los n individuos.
- Unir los dos individuos menos disimiles, obteniendo n - 1 grupos.
- Calcular las disimilitudes entre el nuevo grupo y los demás individuos (se pueden considerar grupos de un solo individuo).
- Unir los dos grupos menos disimiles, obteniendo n - 2 grupos.
- Continuar calculando las disimilitudes entre el nuevo grupo y los demás grupos, para luego, unir los dos grupos menos disimiles, hasta que obtenga un solo grupo con todos los individuos.
El proceso de uniones se representa por medio de un gráfico llamado Dendrograma.
Para un procedimiento de aglomeración jerárquica se debe seleccionar una similitud, disimilitud o distancia entre grupos, que se denomina también criterio de agregación.
6.3.1.1 Algunos criterios de agregación
-
Enlace simple: La distancia entre dos grupos A y B es igual a la distancia de los dos individuos de diferente grupo más cercanos: d(A,B) = \min \{ d(i,l) : i \in A, l \in B \}
Este criterio tiende a producir grupos alargados (efecto de encadenamiento), que pueden incluir elementos muy distintos en los extremos.
-
Enlace completo: La distancia entre los dos grupos A y B es igual a la distancia entre los dos individuos de diferente grupo más alejados: d(A,B) = \max \{ d(i,l) : i \in A, l \in B \}
El enlace completo tiende a producir grupos esféricos.
Ejemplo 6.1 Ilustremos con la distancia de Manhattan y el enlace completo:
a <- c(1,1); b <- c(2,2); c <- c(3,1)
d <- c(3,3); e <- c(3,4); f <- c(5,4)
X <- rbind(a,b,c,d,e,f)
s.label(X, clabel=1)
Las distancias de Manhattan entre individuos son:
D <- dist(X, "manhattan")| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| a | 0 | 2 | 2 | 4 | 5 | 7 |
| b | 2 | 0 | 2 | 2 | 3 | 5 |
| c | 2 | 2 | 0 | 2 | 3 | 5 |
| d | 4 | 2 | 2 | 0 | 1 | 3 |
| e | 5 | 3 | 3 | 1 | 0 | 2 |
| f | 7 | 5 | 5 | 3 | 2 | 0 |
Árbol o Dendrograma:
hc <- hclust(D)
plot(hc, las=1, col="darkblue", main="", sub="", xlab="")
abline(h=0:7, col="gray90", lty=3)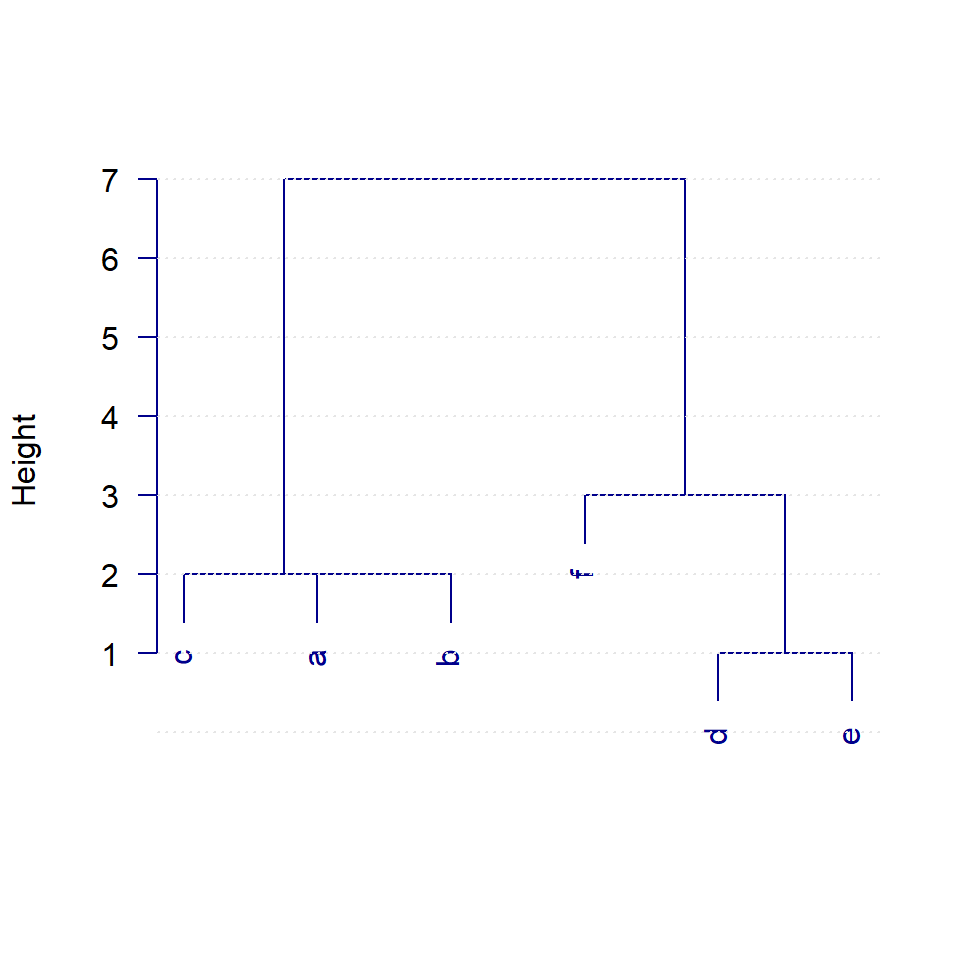
Pasos:
- Se unen d y e a una distancia de 1
- Se unen a y b a una distancia de 2
- Se unen ab y c a una distancia de 2
- Se unen de y f a una distancia de 3
- Se unen abc y def a una distancia de 7
Ultra-métrica asociada al árbol:
| a | b | c | d | e
-------------------
b | 2 |
c | 2 | 2
d | 7 | 7 | 7
e | 7 | 7 | 7 | 1
f | 7 | 7 | 7 | 3 | 36.3.1.2 Método de Ward
Para lograr grupos que tengan inercia “dentro-grupos” / “intra-grupos” mínima se debe utilizar una distancia euclidiana y unir en cada paso del procedimiento los dos grupos que menos aumenten la inercia dentro-grupos. Al incremento de inercia dentro-grupos al unir dos grupos lo llamaremos distancia de Ward entre esos dos grupos y la notaremos W(,). Entonces, al tener tres grupos A, B y C, es necesario calcular W(A, B), W(A, C) y W(B, C) y el menor valor determinará los grupos a unir.
Sean A y B dos grupos o clases no vacías y disyuntas, y sean p_A, p_B y g_A, g_B, los pesos y centros de gravedad de los grupos A y B según el caso.
\begin{aligned} W(A, B) &= p_{_A} d^2(\mathbf{g}_{_{A}},\mathbf{g}_{_{AB}}) + p_{_B} d^2(\mathbf{g}_{_{B}},\mathbf{g}_{_{AB}}) \\ &= \frac{p_{_A} p_{_B}}{p_{_A} + p_{_B}}d^{2}(\mathbf{g}_{_A} , \mathbf{g}_{_B}) \end{aligned}
En particular, para dos individuos i y l (considerados como grupos de un solo elemento), la distancia de Ward es: W(i,l) = \frac{p_i p_l}{p_i + p_l}d^{2}(i,l)
Si los pesos para los dos individuos son iguales a \tfrac{1}{n}, entonces: W(i,l) = \frac{1}{2n}d^{2}(i,l)
Al formar el árbol:
- Antes de empezar las uniones toda la inercia corresponde a inercia entre-grupos (cada individuo es un grupo).
- A medida que llevan a cabo las uniones, la inercia entre-grupos va pasando a inercia dentro-grupos
- Al terminar, toda es inercia dentro-grupos (todos los elementos conforman un grupo)
Ejemplo 6.2 Distancias de Ward entre cafés:
Código
ExCl C40M C40C C20M C20C ExOs O40M O40C O20M O20C Com1
C40M 3.36
C40C 2.36 0.16
C20M 1.26 0.53 0.28
C20C 0.66 1.05 0.54 0.13
ExOs 0.71 3.81 2.46 2.00 1.17
O40M 4.13 0.54 0.42 1.33 1.63 3.35
O40C 2.72 0.97 0.43 1.06 1.04 1.77 0.31
O20M 1.53 1.52 0.71 0.92 0.62 0.73 0.97 0.23
O20C 1.30 1.95 1.03 1.11 0.67 0.45 1.36 0.46 0.04
Com1 1.37 1.83 1.26 1.00 0.64 1.31 1.81 1.38 0.85 0.72
Com2 0.89 2.69 2.01 1.28 0.77 1.29 3.06 2.36 1.45 1.20 0.20Árbol:
hclCafe <- ward.cluster(dista=dist(F), h.clust=1) # función de FactoClass
plot(hclCafe, las=1, col="darkblue", main="", sub="", xlab="")
abline(h=seq(0, 7, 0.5), col="gray90", lty=3)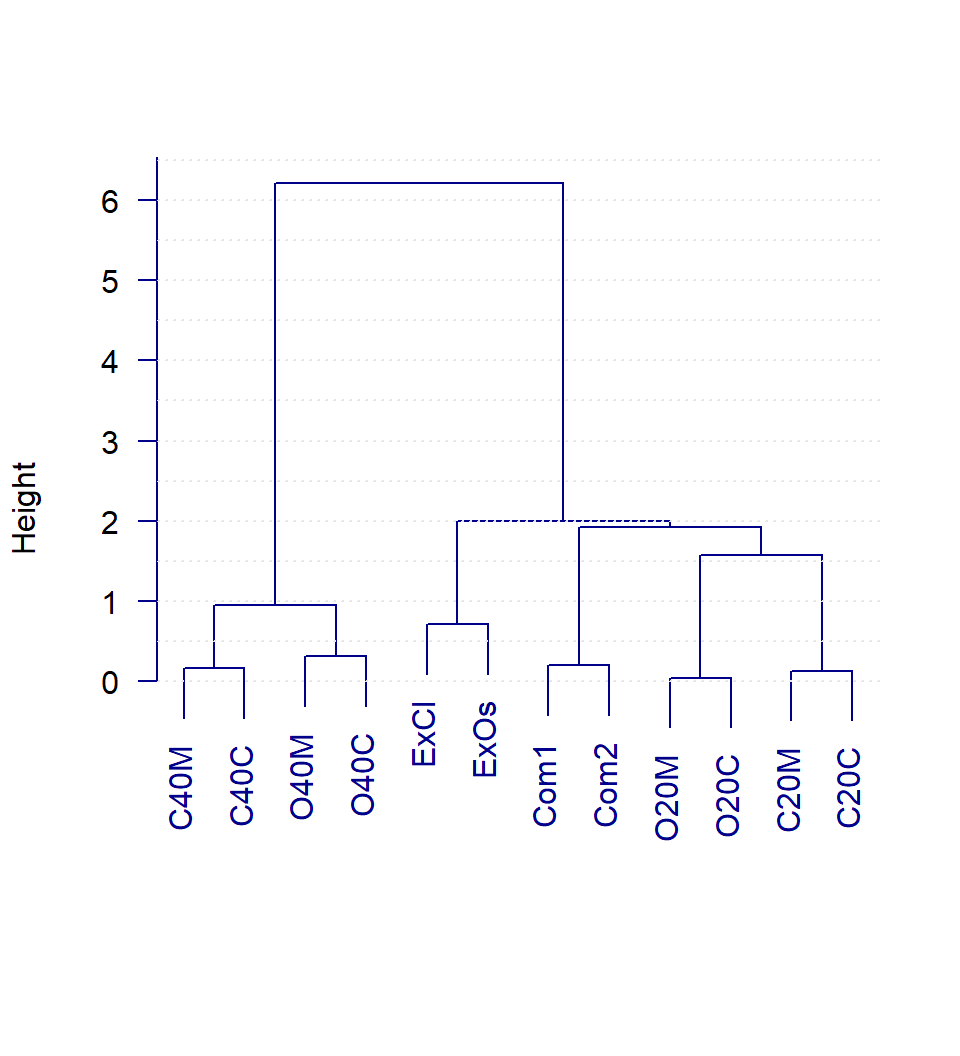
6.4 Agrupamiento directo
En este caso, los métodos suelen requerir: la cantidad de grupos a obtener, valores iniciales para poder empezar y un criterio de parada para poder detenerse. Uno de los métodos más sencillo y más conocido de agrupamiento directo (basado en particiones y basado en centroides) es el de K-means.
6.4.1 Método K-means
Está relacionado con la geometría utilizada en los métodos factoriales porque recurre a la distancia Euclidiana entre individuos.
La distancia entre grupos se calcula como la distancia Euclidiana entre sus respectivos centros de gravedad.
El método K-means busca una partición en K grupos que tenga inercia dentro-grupos mínima, es decir, lo que hace es minimizar las distancias euclidianas al cuadrado entre los individuos y el centro de gravedad del grupo al que pertenecen.
Además, el minimizar esta inercia dentro-grupos coincide con el buscar que los individuos de cada grupo sean lo más “parecidos” entre sí que se pueda (individuos homogéneos dentro de cada grupo).
Por otro lado, como inercia (total) = inercia dentro-grupos + inercia entre-grupos, entonces, también se está buscando que los individuos de grupos distintos sean lo más “diferentes” que se pueda (individuos heterogéneos entre grupos distintos).
6.4.1.1 Algoritmo de Lloyd/Forgy
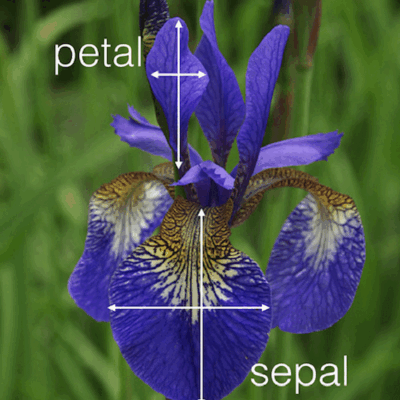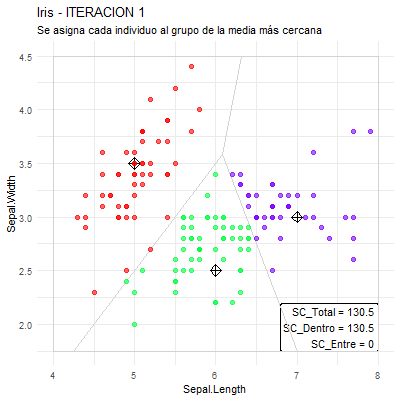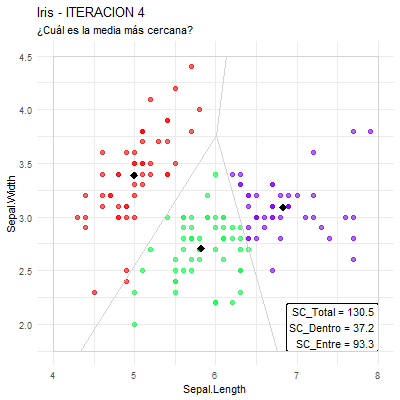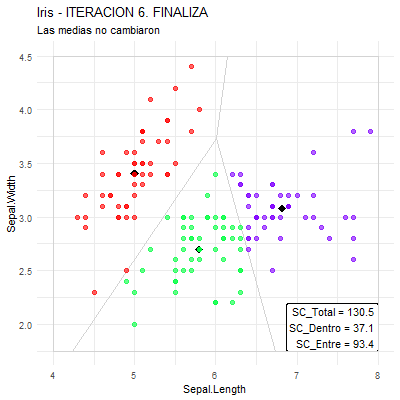
ENTRADA: Tabla de datos de variables cuantitativas y la cantidad de grupos a obtener (K).
- Pedir como entrada o seleccionar K puntos (“centros de gravedad”) iniciales.
Repetir:
- Asignar a cada individuo el grupo cuyo centro de gravedad sea el más cercano.
- Calcular los nuevos centros de gravedad de cada grupo.
Hasta que: los centros de gravedad no cambien.
SALIDA: Conformación de los grupos (asociación individuo-grupo).
6.4.1.2 Ventajas
- Es muy rápido. Usualmente converge en pocas iteraciones.
- Poco exigente en recursos computacionales. Por ejemplo, no requiere calcular distancias entre todos los individuos, basta con calcular las distancias de los individuos a los centros de gravedad de los grupos. Como K suele ser mucho menor a n, la cantidad de distancias a calcular es menor.
6.4.1.3 Aplicaciones
10 Interesting Use Cases for the K-Means Algorithm
https://dzone.com/articles/10-interesting-use-cases-for-the-k-means-algorithm
6.4.1.4 Desventajas
Se debe suministrar la cantidad de grupos a obtener. De alguna manera se debe determinar el número de grupos más adecuado para el conjunto de datos.
El resultado obtenido por el algoritmo depende de los puntos (“centros de gravedad”) iniciales dados. No hay garantía de que la inercia dentro-grupos alcanzada sea un mínimo global, incluso podría estar bastante lejos de serlo.
El método solamente es capaz de identificar adecuadamente grupos de individuos cuando estos se encuentran en regiones separables por “puntos equidistantes” con respecto a los centros de gravedad.
6.5 Combinación de métodos
Los métodos de agrupación de Ward y de K-means son compatibles, ya que los dos buscan la más baja inercia dentro-grupos.
Además, estos dos métodos tienen ventajas y desventajas que se complementan.
-
La recomendación para combinar los métodos sería:
Cuando el número de elementos a agrupar no es tan grande, y el equipo de cálculo lo permite, se realiza la agrupación jerárquica aglomerativa con el método de Ward. Si el número de elementos a clasificar es demasiado grande se puede utilizar el K-means para un pre-agrupamiento (miles de grupos), y luego realizar el agrupamiento jerárquico con los centros de gravedad del pre-agrupamiento.
A partir del Dendrograma, es posible escoger un corte del árbol que nos daría la cantidad de grupos potencialmente más adecuada.
Luego, con los centros de gravedad dados por el corte en el árbol, utilizar el K-means para disminuir tanto como se pueda la inercia dentro-grupos, y así mejorar o consolidar la agrupación respectiva.
6.6 Agrupamiento a partir de ejes factoriales
Los métodos factoriales se pueden utilizar para transformar los datos antes de realizar procedimientos de agrupación. Estos métodos pueden cumplir dos funciones: reducir la dimensión de los datos y cuantificar las variables cualitativas. Por ejemplo:
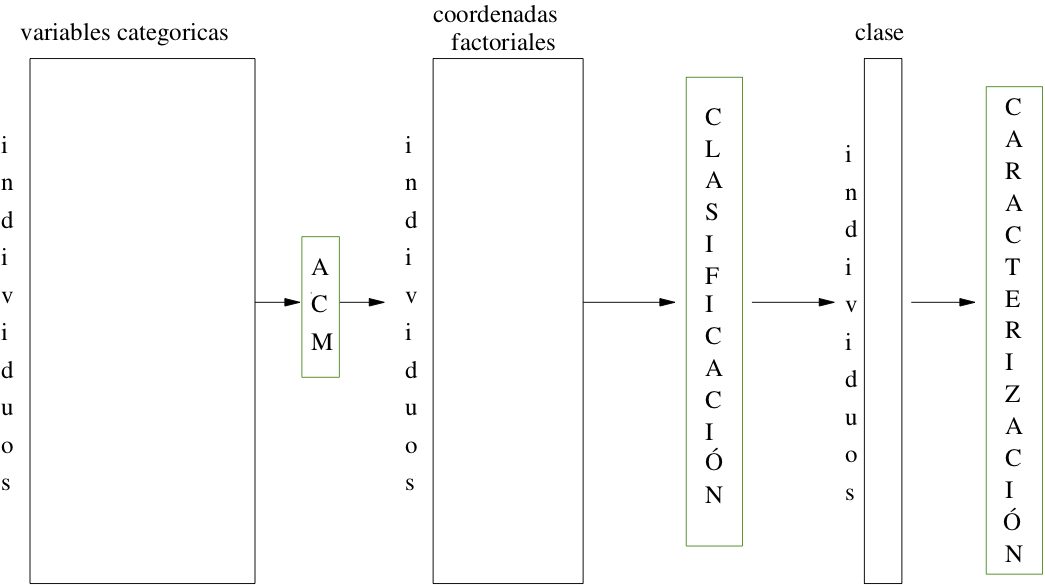
6.7 Caracterización automática de grupos
Luego de obtener los grupos de individuos, es natural el querer identificar las características que distinguen a cada grupo, de los demás grupos, o del conjunto completo de individuos.
Como al agrupar se obtiene una nueva variable cualitativa a partir de los datos, esta nueva variable se puede contrastar con las demás mediante un análisis bivariado. En particular, se pueden utilizar los valores test:
Para una variable cuantitativa, los valores test son valores indicativos de que tan lejos, en desviaciones estándar, está la media de la variable cuantitativa para los individuos de un grupo, con respecto a la media general o global de la variable.
En el caso de una variable cualitativa, un valor test nos indica que tan diferente es la frecuencia de una categoría dentro de un grupo, con respecto a su frecuencia global.
Las variables cuantitativas o las categorías de las variables cualitativas con un valor test en magnitud superior a un umbral se dice que caracterizan al grupo.
6.8 Estrategia completa de agrupamiento
La estrategia completa de agrupamiento que se propondría, se resume en los siguientes pasos:
- Realizar el análisis en ejes factoriales que corresponda.
- Seleccionar el número de ejes factoriales para el agrupamiento.
- Si el número de “individuos” es muy grande, realizar un K-means de pre-agrupamiento en miles de grupos.
- Realizar el agrupamiento jerárquico con el método de Ward sobre los “individuos” o los grupos del paso anterior.
- Decidir el número de grupos y cortar el árbol.
- Realizar un K-means de consolidación, partiendo de los centros de gravedad de la partición obtenida al cortar el árbol.
- Caracterizar los grupos.
- Proyectar los grupos sobre los planos factoriales.
6.9 Ejemplo de “juguete” (admitidos)
A continuación se procederá a realizar la agrupación de admitidos. Este análisis es complementario al realizado en la sesión anterior. Las variables activas son género, edad, estrato y origen, y las variables ilustrativas, los resultados del examen de admisión (continuas) y la carrera.
Código
gene edad estr orig
1 F a17 alto Bogo
2 M a17 medio Bogo
3 F a18 bajo Bogo
4 F a18 bajo Bogo
5 M a17 medio Bogo
6 F a17 medio Bogo
7 F a17 medio Bogo
8 M a17 medio Bogo
9 F a19M medio Bogo
10 M a18 medio BogoSiguiendo la estrategia completa de agrupamiento propuesta:
1. El análisis en ejes factoriales que corresponde es un ACM.
Código
# OPCIÓN 1:
# ejecuta de forma interactiva:
fc <- FactoClass(Y, dudi.acm, admi[, 1:7])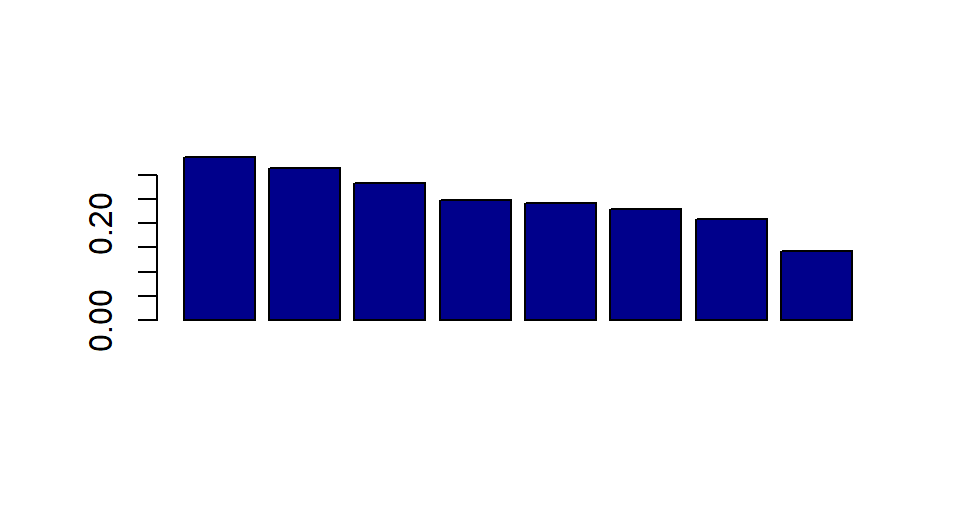
2. Se seleccionan seis (6) ejes.
3. No se requiere un K-means de pre-agrupamiento.
4. Indices de la agrupación jerárquica:
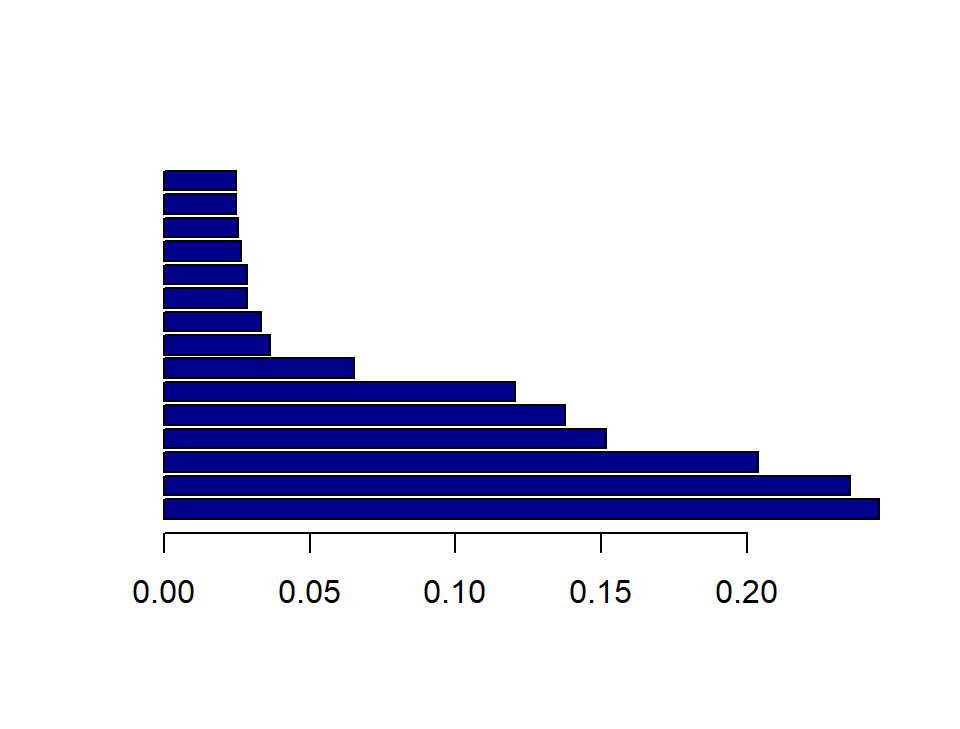
5. Se hace el corte para ocho (8) grupos.
6. Cambios debidos al K-means:
Código
fc$clus.summ[, 1:4] Bef.Size Aft.Size Bef.Inertia Aft.Inertia
1 68 68 0.100 0.100
2 55 55 0.018 0.018
3 54 54 0.081 0.081
4 77 48 0.107 0.038
5 62 62 0.056 0.056
6 58 66 0.025 0.035
7 38 38 0.082 0.082
8 33 54 0.021 0.054
TOTAL 445 445 0.490 0.4647. Valores test para la caracterización:
Código
# Valores test variables cuantitativas
fc$carac.contCódigo
# Valores test categorías de v. cualitativas
fc$carac.cate8. Gráfico del primer plano factorial:
Código
plotFactoClass(fc, x=1, y=2, cex.col=0.5,
roweti="", infaxes="no", cstar=0)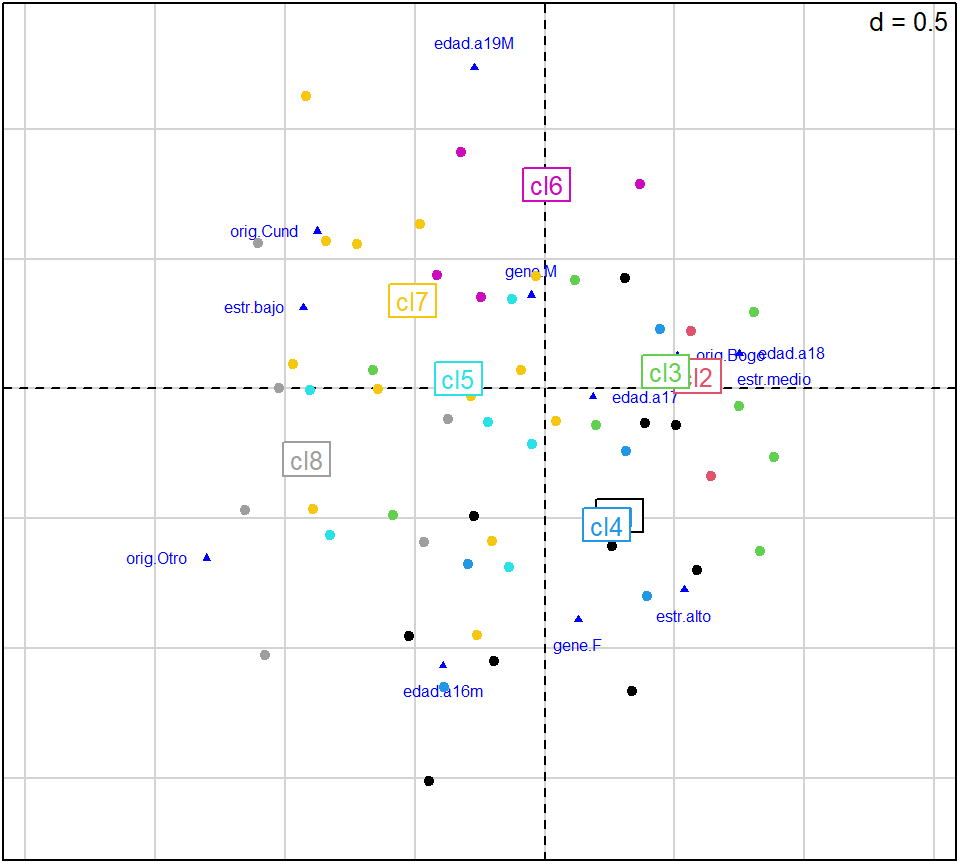
Si así lo prefiere, para seguir los pasos de la estrategia completa de agrupamiento, también puede optar por utilizar el paquete Factoshiny. Basta con:
- Hacer el análisis factorial que corresponda. Por ejemplo, para los datos de Adjetivos × Colores de la sesión 2, se requeriría un ACS (la función correspondiente sería
CAshiny()):
Seleccionar la opción “Perform clustering after leaving CA app?”.
Indicar el número de ejes a conservar para el agrupamiento.
Dar clic en “Quit the app”.
Este último paso abre la aplicación web que tiene como título: “HCPC on the dataset”, que es la encargada específicamente de la parte del agrupamiento, a partir de los resultados del análisis factorial.