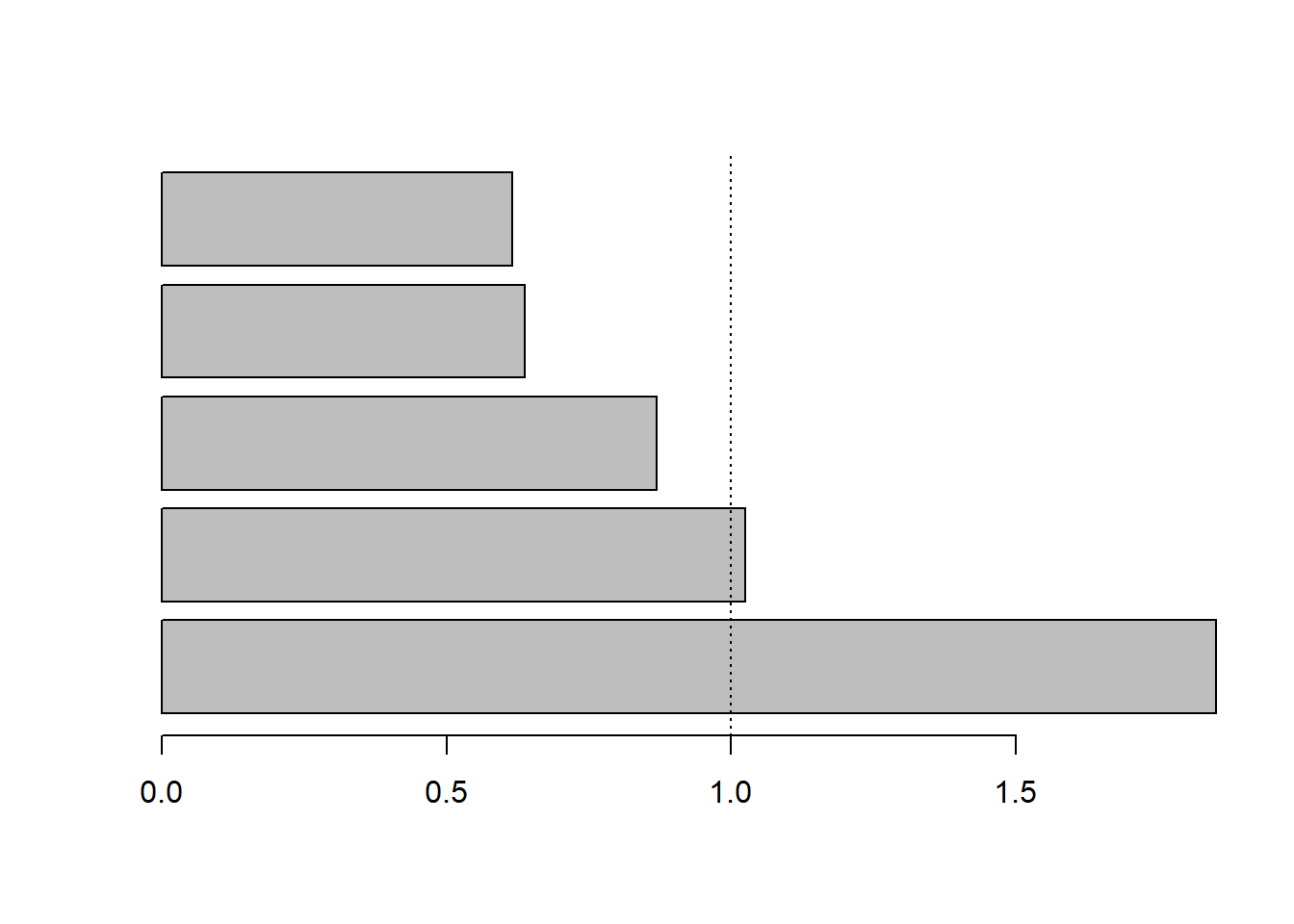2 ACP

Código a ejecutar antes de empezar:

# 4 cifras significativas y sin notación científica:
options(digits = 4, scipen = 999) 
# cargar librerías: 
library(FactoClass)
library(factoextra)
library(knitr) # para función kable (tablas estáticas)
library(DT) # para tablas interactivas
library(plotly) # para gráficos interactivos

El análisis de componentes principales (ACP) es un procedimiento estadístico que utiliza una transformación para convertir un conjunto de observaciones de variables numéricas posiblemente correlacionadas en un conjunto de valores de variables no correlacionadas linealmente llamadas componentes principales. Las componentes principales son combinación lineal (suma ponderada) de las variables originales.

El ACP permite reducir la dimensión (de manera lineal), describir relaciones lineales entre variables y comparar individuos a partir de la distancia entre ellos.

Esta transformación se define de tal manera que el primer componente principal tiene la mayor variabilidad posible (es decir, representa la mayor cantidad posible de variabilidad en los datos), y cada componente subsiguiente, a su vez, tiene la mayor variabilidad posible bajo la restricción de ser ortogonal (perpendicular) a las componentes anteriores.

A continuación utilizaremos el ejemplo que se presenta en la pág. 41 del libro. Adicionalmente, este es un extracto del resumen (abstract) del artículo origen de los datos:

“Ocasionalmente el café tostado y molido es objeto de adulteraciones, mediante la adición de toda clase de materiales extraños. Debido a que estos adulterantes modifican notablemente las características sensoriales, químicas y físicas del café, es necesario desarrollar métodos de análisis que permitan establecer el grado contenido en un producto comercial. En este estudio se analizaron 14 muestras y se realizaron determinaciones de color, acidez titulable, extracto acuoso, contenido de ácidos clorogénicos, cafeína, intensidad del aroma, acidez, amargo y cuerpo, entre otros. Se buscó sintetizar la información contenida en cada una de las determinaciones, con el fin de obtener tanto relaciones entre éstas, así como una evaluación de las muestras estudiadas. Con el análisis estadístico multivariado por componentes principales realizado se logró reducir la dimensión del problema de 16 variables estudiadas a sólo 3 factores, manteniéndose representativamente el 85,36% de la variación total…”

Duarte et al. (1996). Análisis multivariado por componentes principales, de cafés tostados y molidos adulterados con cereales. Cenicafé, 478(2):65-76

Análisis de cafés tostados y molidos adulterados con cereales

Se usa una identificación nemotécnica de los individuos, que corresponden a 2 marcas comerciales de café y a 10 tratamientos del experimento (Agregado: Sin, Maíz, Cebada. Porcentaje del Agregado: 0, 20% y 40%. Grado de tostión: Clara y Oscura).

data(cafe) # cargar datos cafe de FactoClass
n <- nrow(cafe) # n: número de individuos
kable(cafe)

	Color	DA	EA	pH	AcidezT	Cafeina	AcidosCl	D2325	D2272	Intensidad	Aroma	Cuerpo	Acidez	Amargo	Astringencia	Impresion
ExCl	298	385.1	25	5.02	11.7	1.40	2.74	-0.101	-0.057	7.72	7.00	6.84	5.02	5.04	5.36	7.46
C40M	361	481.3	41	5.11	6.5	0.81	1.62	-0.058	-0.038	6.02	5.42	6.22	4.34	4.60	4.78	6.24
C40C	321	422.6	40	5.12	5.8	0.80	1.61	-0.057	-0.038	6.48	5.98	6.44	4.58	4.82	4.80	6.12
C20M	335	444.3	33	5.05	8.8	1.10	2.20	-0.079	-0.045	6.82	6.44	6.70	4.62	4.38	4.80	6.04
C20C	314	368.7	32	5.04	9.3	1.10	2.19	-0.080	-0.046	7.08	6.20	6.72	4.78	4.94	4.90	6.22
ExOs	186	346.6	28	5.31	8.7	1.35	2.30	-0.049	-0.064	7.66	7.42	6.98	5.12	5.18	5.22	7.40
O40M	278	422.6	43	5.45	4.9	0.80	1.35	-0.025	-0.037	6.18	5.82	6.26	4.00	4.46	4.96	5.90
O40C	238	403.0	42	5.33	5.2	0.79	1.36	-0.026	-0.036	6.84	6.56	6.82	4.30	4.96	4.84	6.94
O20M	226	368.7	36	5.33	6.7	1.10	1.83	-0.035	-0.051	6.66	7.06	6.70	4.64	5.00	4.90	6.90
O20C	210	368.7	35	5.31	7.0	1.05	1.83	-0.040	-0.056	7.00	6.70	7.04	4.60	4.88	5.18	7.16
Com1	221	413.3	27	5.18	9.3	1.30	2.06	-0.053	-0.065	6.48	5.46	7.06	4.60	5.26	5.16	5.68
Com2	264	400.9	23	5.20	11.5	1.35	2.84	-0.096	-0.051	6.66	6.26	7.36	4.44	5.64	5.24	6.00

summary(cafe)

     Color           DA            EA             pH          AcidezT     
 Min.   :186   Min.   :347   Min.   :23.0   Min.   :5.02   Min.   : 4.90  
 1st Qu.:225   1st Qu.:369   1st Qu.:27.8   1st Qu.:5.09   1st Qu.: 6.33  
 Median :271   Median :402   Median :34.0   Median :5.19   Median : 7.85  
 Mean   :271   Mean   :402   Mean   :33.8   Mean   :5.20   Mean   : 7.95  
 3rd Qu.:316   3rd Qu.:423   3rd Qu.:40.2   3rd Qu.:5.32   3rd Qu.: 9.30  
 Max.   :361   Max.   :481   Max.   :43.0   Max.   :5.45   Max.   :11.70  
    Cafeina         AcidosCl        D2325             D2272        
 Min.   :0.790   Min.   :1.35   Min.   :-0.1010   Min.   :-0.0650  
 1st Qu.:0.807   1st Qu.:1.62   1st Qu.:-0.0793   1st Qu.:-0.0563  
 Median :1.100   Median :1.95   Median :-0.0550   Median :-0.0485  
 Mean   :1.079   Mean   :1.99   Mean   :-0.0583   Mean   :-0.0487  
 3rd Qu.:1.312   3rd Qu.:2.23   3rd Qu.:-0.0387   3rd Qu.:-0.0380  
 Max.   :1.400   Max.   :2.84   Max.   :-0.0250   Max.   :-0.0360  
   Intensidad       Aroma          Cuerpo         Acidez         Amargo    
 Min.   :6.02   Min.   :5.42   Min.   :6.22   Min.   :4.00   Min.   :4.38  
 1st Qu.:6.48   1st Qu.:5.94   1st Qu.:6.63   1st Qu.:4.42   1st Qu.:4.76  
 Median :6.74   Median :6.35   Median :6.77   Median :4.60   Median :4.95  
 Mean   :6.80   Mean   :6.36   Mean   :6.76   Mean   :4.59   Mean   :4.93  
 3rd Qu.:7.02   3rd Qu.:6.78   3rd Qu.:7.00   3rd Qu.:4.67   3rd Qu.:5.08  
 Max.   :7.72   Max.   :7.42   Max.   :7.36   Max.   :5.12   Max.   :5.64  
  Astringencia    Impresion   
 Min.   :4.78   Min.   :5.68  
 1st Qu.:4.83   1st Qu.:6.03  
 Median :4.93   Median :6.23  
 Mean   :5.01   Mean   :6.50  
 3rd Qu.:5.19   3rd Qu.:7.00  
 Max.   :5.36   Max.   :7.46

Imagine un análisis bivariado de todas las anteriores variables (un análisis de todos los posibles pares de variables)

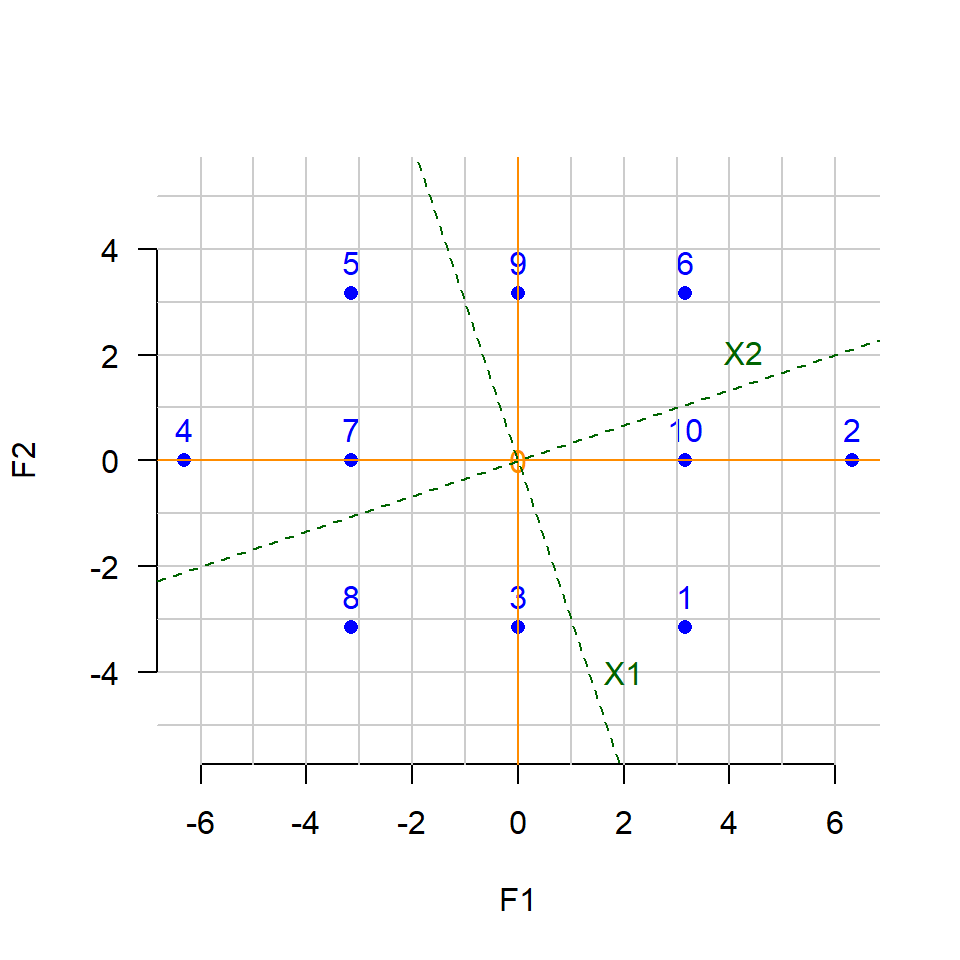
Para comenzar con un enfoque descriptivo multivariado, tomemos solamente los datos de dos individuos y tres variables (numéricas). Esta matriz, que denotaremos como Y, está conformada por vectores fila que representan a los individuos y por vectores columna que representan a las variables.

Aux <- cafe[c(1,6), 1:3]
kable(Aux)

	Color	DA	EA
ExCl	298	385.1	25
ExOs	186	346.6	28

A partir de dicha matriz, es posible tener una representación gráfica por vectores fila (nube de individuos) y otra por vectores columna (nube de variables).

fig <- plot_ly(Aux, x = ~Color, y = ~DA, z = ~EA)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(Aux))
fig <- fig %>% layout(title = "vectores fila\n(individuos)",
                      scene = list(xaxis = list(range = c(0,400)),
                                   yaxis = list(range = c(0,400)),
                                   zaxis = list(range = c(0,40))),
                      showlegend = FALSE)
fig

tAux <- as.data.frame(t(Aux))
fig <- plot_ly(tAux, x = ~ExCl, y = ~ExOs)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(tAux), textposition = "top")
fig <- fig %>% layout(title = "vectores columna\n(variables)",
                      xaxis = list(range = c(-10,400)),
                      yaxis = list(range = c(-10,400)),
                      showlegend = FALSE)
fig

2.1 La nube de individuos

Cada punto corresponderá a un vector fila y representará a un individuo en un espacio de tantas dimensiones como variables.

Y <- cafe[1:10 ,1:3]
n <- nrow(Y) 
p <- ncol(Y)
kable(Y)

	Color	DA	EA
ExCl	298	385.1	25
C40M	361	481.3	41
C40C	321	422.6	40
C20M	335	444.3	33
C20C	314	368.7	32
ExOs	186	346.6	28
O40M	278	422.6	43
O40C	238	403.0	42
O20M	226	368.7	36
O20C	210	368.7	35

2.1.1 Centro de gravedad

Es una suma ponderada de los vectores fila (uno vector por individuo). \vec{\mathrm{g}} = \sum_{i = 1}^n p_i \vec{y}_i

Cuando todos los pesos p_i son iguales a \frac{1}{n} (o lo que es lo mismo, cuando todos los individuos tienen el mismo peso o ponderación), es la suma de los vectores fila, para luego dividir por la cantidad de individuos, \begin{aligned} \vec{\mathrm{g}} &= \frac{\vec{y}_1 + \vec{y}_2 + \dots + \vec{y}_n}{n} \\ &= \frac{1}{n} \vec{y}_1 + \frac{1}{n} \vec{y}_2 + \dots + \frac{1}{n} \vec{y}_n \\ &= \sum_{i = 1}^n \frac{1}{n} \vec{y}_i \end{aligned}

par(las = 1) # gráfica
Y3D <- scatterplot3d(Y, main = "Y", type = "h", color = 4, 
                     box = FALSE, las = 1)
Y3D$points3d(Y, pch = 16, col = 4)
addgrids3d(Y, grid = c("xy","xz","yz"))
cord2d <- Y3D$xyz.convert(Y) # convertir coordenadas 3D a 2D
# poner etiquetas:
text(cord2d, labels = rownames(Y), cex = 0.8, pos = 3)

g <- colMeans(Y) # centro de gravedad
Y3D$points3d(t(g), pch = 19, col = 3, type = "h")
text(Y3D$xyz.convert(t(g)), labels = "g", 
     pos = 3, cex = 1.3)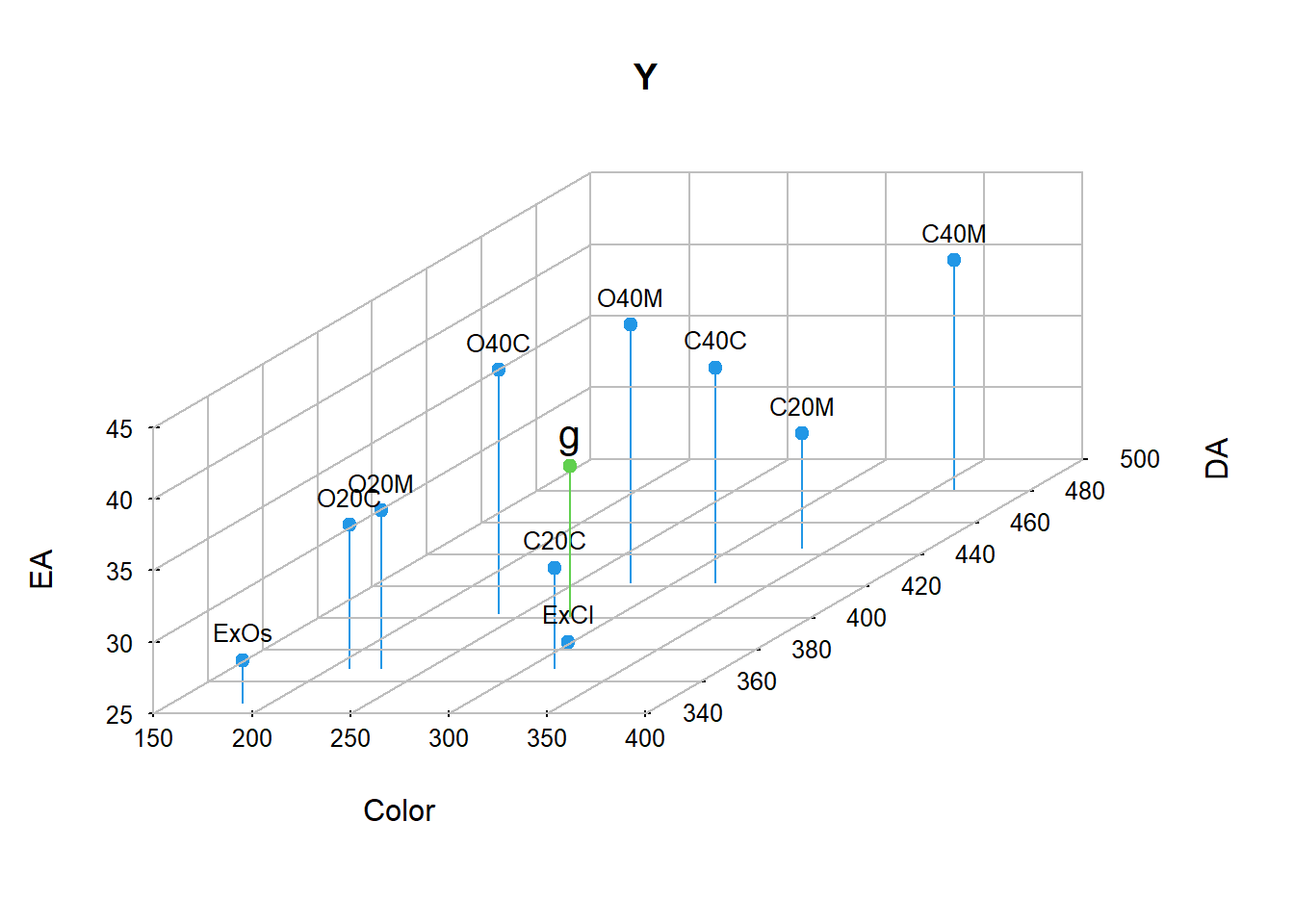

2.1.2 Centrado

Centrar los puntos es hacer que el centro de gravedad quede en el origen de las coordenadas (“en el cero”).

A cada vector fila se le resta el vector de medias, de esta manera se da una traslación de todos los individuos. Esta operación se escribiría así para cada vector fila (para el i-ésimo): \vec{y}_{Ci} = \vec{y}_i - \vec{\mathrm{g}} y matricialmente para todos los individuos a la vez, así: Y_C = Y - \mathbf{1}_n \, \vec{\mathrm{g}}'

par(las = 1)
unos <- rep(1, n) # vector de n unos
Yc <- Y - unos %*% t(g)
kable(Yc)

	Color	DA	EA
ExCl	21.3	-16.06	-10.5
C40M	84.3	80.14	5.5
C40C	44.3	21.44	4.5
C20M	58.3	43.14	-2.5
C20C	37.3	-32.46	-3.5
ExOs	-90.7	-54.56	-7.5
O40M	1.3	21.44	7.5
O40C	-38.7	1.84	6.5
O20M	-50.7	-32.46	0.5
O20C	-66.7	-32.46	-0.5

# grafica de datos centrados
Yc3D <- scatterplot3d(Yc, main = "Yc", type = "h", 
                      color = 4, box = FALSE, las = 1)
Yc3D$points3d(Yc, pch = 16, col = 4)
addgrids3d(Yc, grid = c("xy","xz","yz"))
text(Yc3D$xyz.convert(Yc), labels = rownames(Yc), 
     cex = 0.8, pos = 3)
Yc3D$points3d(t(c(0,0,0)), pch = 19, col = 3, type = "h")
text(Yc3D$xyz.convert(t(c(0,0,0))), labels = "0", 
     pos = 3, cex = 1.3)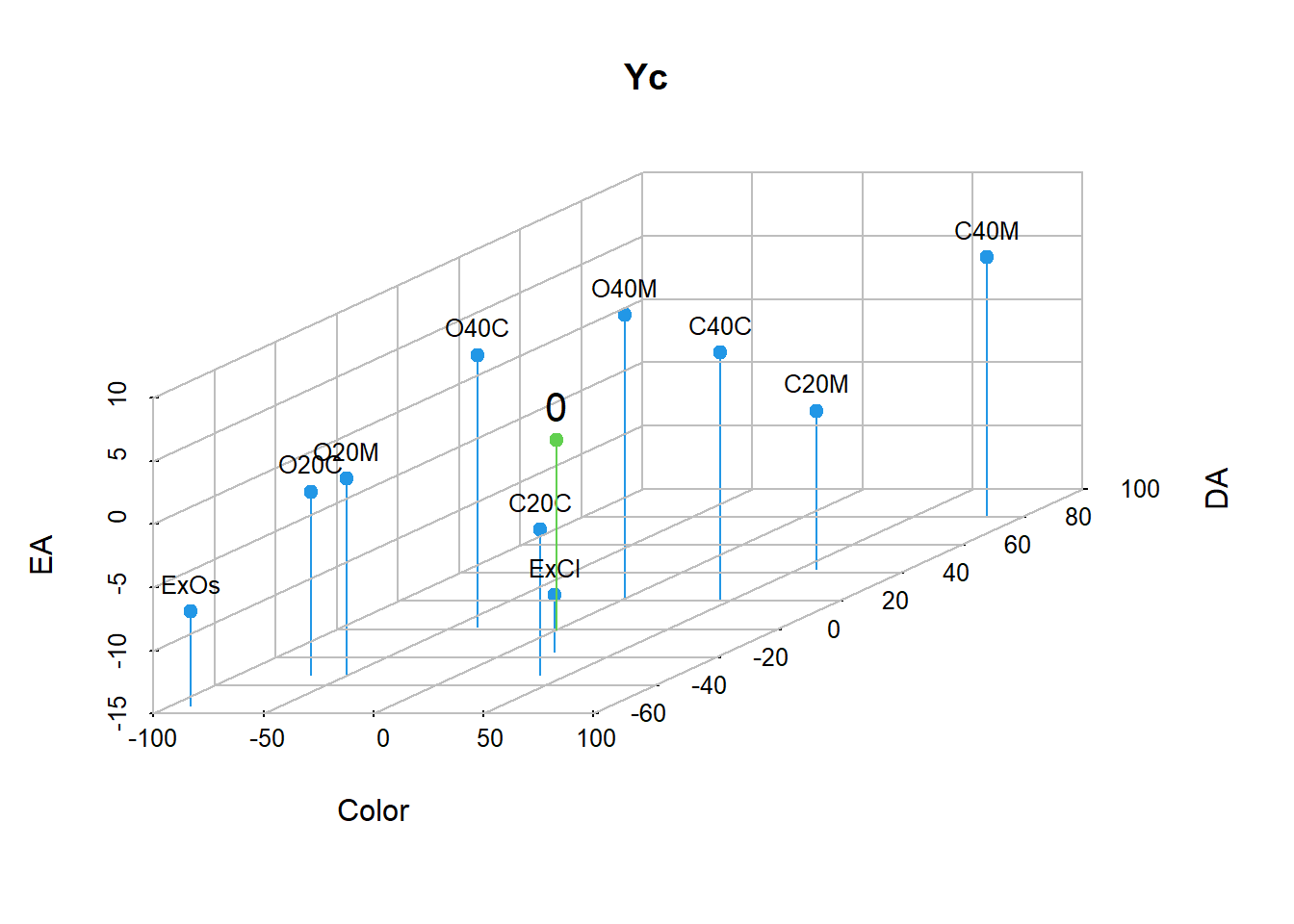

2.1.3 Distancia entre individuos

fig <- plot_ly(Yc, x = ~Color, y = ~DA, z = ~EA)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(Yc))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)
fig <- fig %>% layout(showlegend = FALSE)
fig

La distancia euclidiana al cuadrado entre dos individuos (dos vectores fila) es la suma de las diferencias al cuadrado de sus componentes variable por variable: d^2(\vec{y}_i,\vec{y}_l) = \sum_{j=1}^p ( y_{ij} - y_{lj} )^2 Suma ponderada en donde cada diferencia al cuadrado (una por cada variable) tiene la misma ponderación: 1.

(d <- round(dist(Y), 1))

      ExCl  C40M  C40C  C20M  C20C  ExOs  O40M  O40C  O20M
C40M 116.1                                                
C40C  46.5  71.0                                          
C20M  70.3  45.9  26.8                                    
C20C  24.0 122.3  54.9  78.5                              
ExOs 118.5 221.2 155.4 178.2 130.0                        
O40M  46.2 101.7  43.1  61.8  65.7 120.3                  
O40C  64.9 145.8  85.3 105.8  84.0  78.0  44.6            
O20M  74.7 175.9 109.3 132.7  88.1  46.4  75.2  36.8      
O20C  90.1 188.5 123.5 146.1 104.0  33.4  87.1  44.8  16.0

summary(as.vector(d))

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   16.0    46.5    84.0    90.7   120.3   221.2

length(as.vector(d))

[1] 45

2.1.4 Inercia

La inercia de la nube de individuos es, \begin{aligned} Inercia(N_n) &= \sum\limits_{i=1}^{n}{p_i \, d^2\left(\vec{y}_i,\vec{\mathbf{g}}\right)} \\ &= \sum\limits_{i=1}^{n}{p_i \, d^2\left(\vec{y}_{Ci} ,\vec{0}\right)} \\ &= \sum\limits_{i=1}^{n}{p_i \, \left(\sum\limits_{j=1}^{p}y_{{_C}_{ij}}^2\right)} \end{aligned} Cuando todos los pesos p_i son iguales a \frac{1}{n}, \begin{aligned} Inercia(N_n) &= \dfrac{1}{n}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{p}y_{{_C}_{ij}}^2 \\ &= \sum\limits_{j=1}^{p}\dfrac{1}{n}\sum\limits_{i=1}^{n}y_{{_C}_{ij}}^2 \\ &= \sum\limits_{j=1}^{p}\sigma_j^2 \end{aligned}

Concluimos que la inercia de la nube de individuos es la suma de las varianzas de las variables.

La matriz de varianzas y covarianzas de \mathbf{Y} (que es la misma matriz de varianzas y covarianzas de \mathbf{Y}_C) es, V=\dfrac{1}{n} Y'_C Y_C La suma de las varianzas, es decir la inercia de la nube de individuos, es igual a traza(V).

2.1.5 Reducción

Si a cada término de la matriz Y lo centramos y lo reducimos (lo estandarizamos), entonces obtenemos, x_{ij}=\dfrac{y_{ij}-\bar{y}_j}{\sigma_j} donde \bar{y}_j y \sigma_j son respectivamente la media y la desviación estándar de la variable j.

Matricialmente, X = Y_C \, D_{\sigma}^{-1} donde D_{\sigma}=diag(\sigma_{_j}).

var(Y)*(n-1)/n

        Color     DA     EA
Color 3105.81 1738.4  60.95
DA    1738.39 1560.2 129.36
EA      60.95  129.4  33.45

(V <- t(Yc) %*% as.matrix(Yc)/n)

        Color     DA     EA
Color 3105.81 1738.4  60.95
DA    1738.39 1560.2 129.36
EA      60.95  129.4  33.45

Dsigma <- diag(sqrt(diag(V))) 
round(diag(Dsigma), 1)

[1] 55.7 39.5  5.8

X <- as.matrix(Yc) %*% solve(Dsigma)
colnames(X) <- colnames(Y)
kable(as.data.frame(X), digits = 1)

	Color	DA	EA
ExCl	0.4	-0.4	-1.8
C40M	1.5	2.0	1.0
C40C	0.8	0.5	0.8
C20M	1.0	1.1	-0.4
C20C	0.7	-0.8	-0.6
ExOs	-1.6	-1.4	-1.3
O40M	0.0	0.5	1.3
O40C	-0.7	0.0	1.1
O20M	-0.9	-0.8	0.1
O20C	-1.2	-0.8	-0.1

par(las = 1) # etiquetas en los dos ejes serán horizontales
X3D <- scatterplot3d(X, main = "X", type = "h", 
                     box = FALSE, color = 4, asp = 1)
X3D$points3d(X, pch = 16, col = 4)
addgrids3d(X, grid = c("xy","xz","yz"))
text(X3D$xyz.convert(X), labels = rownames(X), cex =0.8, pos =3)
X3D$points3d(t(c(0,0,0)), pch = 19, col = 3, type = "h")
text(X3D$xyz.convert(t(c(0,0,0))), labels = "0", 
     pos = 3, cex = 1.3)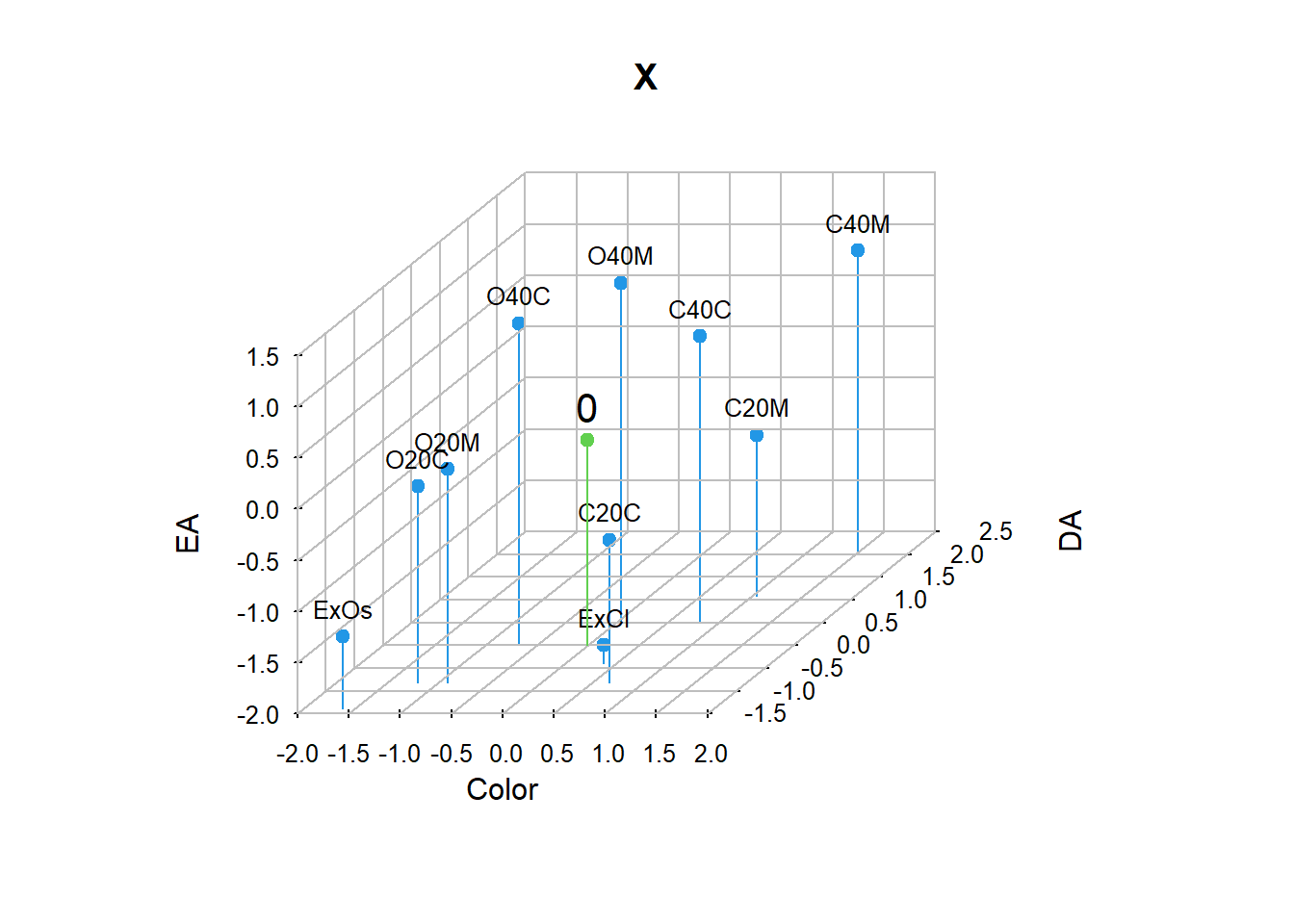

V <- var(Y)*(n-1)/n # Varianza poblacional
Dsigma <- diag(sqrt(diag(V))) # Desv. estandar 
X <- as.matrix(Yc) %*% solve(Dsigma)
colnames(X) <- colnames(Y)
X <- as.data.frame(X)
fig <- plot_ly(X, x = ~Color, y = ~DA, z = ~EA)
fig <- fig %>% add_markers(text = rownames(X))
fig <- fig %>% add_text(text = rownames(X))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)
fig <- fig %>% layout(showlegend = FALSE)
fig

fig <- plot_ly(X, x = ~Color, y = ~DA)
fig <- fig %>% add_markers(text = rownames(X))
fig <- fig %>% add_text(text = rownames(X), textposition = "top")
fig <- config(fig, displayModeBar = FALSE) %>% 
         layout(xaxis = list(range = c(-2.5,2.5)),
                      yaxis = list(range = c(-2.5,2.5)),
                      showlegend = FALSE)
fig

fig <- plot_ly(X, x = ~Color, y = ~EA)
fig <- fig %>% add_markers(text = rownames(X))
fig <- fig %>% add_text(text = rownames(X), textposition = "top")
fig <- config(fig, displayModeBar = FALSE) %>% 
         layout(xaxis = list(range = c(-2.5,2.5)),
                      yaxis = list(range = c(-2.5,2.5)),
                      showlegend = FALSE)
fig

fig <- plot_ly(X, x = ~DA, y = ~EA)
fig <- fig %>% add_markers(text = rownames(X))
fig <- fig %>% add_text(text = rownames(X), textposition = "top")
fig <- config(fig, displayModeBar = FALSE) %>% 
         layout(xaxis = list(range = c(-2.5,2.5)),
                yaxis = list(range = c(-2.5,2.5)),
                showlegend = FALSE)
fig

(d <- round(dist(X),1))

     ExCl C40M C40C C20M C20C ExOs O40M O40C O20M
C40M  3.9                                        
C40C  2.8  1.7                                   
C20M  2.1  1.7  1.4                              
C20C  1.3  3.4  1.9  2.0                         
ExOs  2.3  5.2  3.7  3.7  2.5                    
O40M  3.3  2.1  0.9  2.1  2.4  3.6               
O40C  3.2  3.0  1.6  2.6  2.4  3.0  0.9          
O20M  2.3  3.8  2.3  2.8  1.7  1.7  2.0  1.4     
O20C  2.4  4.1  2.6  3.0  1.9  1.4  2.3  1.6  0.3

summary(as.vector(d))

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.30    1.70    2.30    2.41    3.00    5.20

La matriz de varianzas y covarianzas de X (que es la misma matriz de correlaciones de \mathbf{Y}_C y de \mathbf{Y}) es, V_X= \dfrac{1}{n} X'X

var(X)*(n-1)/n

       Color     DA     EA
Color 1.0000 0.7897 0.1891
DA    0.7897 1.0000 0.5663
EA    0.1891 0.5663 1.0000

X <- as.matrix(X)
( V <- ( t(X) %*% X )/n ) # = var(X)*(n-1)/n

       Color     DA     EA
Color 1.0000 0.7897 0.1891
DA    0.7897 1.0000 0.5663
EA    0.1891 0.5663 1.0000

cor(Y)

       Color     DA     EA
Color 1.0000 0.7897 0.1891
DA    0.7897 1.0000 0.5663
EA    0.1891 0.5663 1.0000

Además, la inercia de la nube de individuos con sus coordenadas estandarizadas es, \begin{aligned} Inercia\left(N_{n_X}\right) &= 1 + 1 + \dots + 1 = p \end{aligned}

2.1.6 Nuevos ejes (cambio de base)

“A function \left\langle \,\cdot ,\cdot \,\right\rangle :\mathbb{R}^{p}\times \mathbb{R}^{p}\to \mathbb{R} is an inner product on \mathbb{R}^{p} if and only if there exists a symmetric positive-definite matrix \mathbf{M} such that \left\langle u,v\right\rangle =u' \mathbf {M} v for all u,v \in \mathbb {R} ^{p}. If \mathbf{M} is the identity matrix then \left\langle u,v\right\rangle =u' \mathbf{M} v = u' v is the dot product.”

Norma:

\left\| u \right\|^2 = \left\langle u,u\right\rangle

Ángulo:

\begin{aligned} \cos\left(\angle_{\vec{u}}^{\vec{v}}\right) &= \frac{\left\langle u,v \right\rangle}{\left\| u \right\| \left\| v \right\|} \end{aligned} de donde se tiene que, \left\langle u,v \right\rangle = \cos\left(\angle_{\vec{u}}^{\vec{v}}\right) \left\| u \right\| \left\| v \right\|

La proyección ortogonal de un vector x_i (individuo i-ésimo) sobre un vector unitario u (\left\| u \right\| = 1) es, \begin{aligned} &\left\| x_i \right\| \cos\left(\angle_{\vec{u}}^{\vec{v}}\right) \\ &= \left\| x_i \right\| \frac{\left\langle x_i,u \right\rangle}{\left\| x_i \right\| \left\| u \right\|} \\ &= \left\langle x_i,u \right\rangle \end{aligned}

La inercia de la nube de individuos sobre la recta que genera el vector u es, \begin{aligned} \sum_{i = 1}^{n} p_i \, d^2\left(\left\langle x_i,u \right\rangle, 0\right) &= \frac{1}{n} \sum_{i = 1}^{n} \left(\left\langle x_i,u \right\rangle\right)^2 \\ &= \frac{1}{n} \sum_{i = 1}^{n} \left( x_i' u \right)^2 \\ &= \frac{1}{n} \left(Xu\right)' \left(Xu\right) \\ &= \frac{1}{n} u'X'Xu \\ &= u' \left( \frac{1}{n} X'X \right) u \\ &= u' \, V_X \, u \end{aligned}

¿Cuál sería el vector unitario que hace que la inercia de la nube sobre la recta que genera el vector sea la máxima posible?

\begin{aligned} {\underset {u \in \mathbb{R}^p}{\text{arg max}}}\quad & u' \left( \frac{1}{n} X'X \right) u \\ {\text{subject to}}\quad &u'u - 1 = 0. \end{aligned}

Usando multiplicadores de Lagrange, f(u) = u' \left( \frac{1}{n} X'X \right) u - \lambda \left( u'u - 1 \right) que tiene como primera derivada, \frac{d}{du} f(u) = 2 \left( \frac{1}{n} X'X \right) u - 2 \lambda u Igualando a cero, \begin{aligned} 2 \left( \frac{1}{n} X'X \right) u - 2 \lambda u &= 0 \\ \left( \frac{1}{n} X'X \right) u &= \lambda u \\ V_X \, u &= \lambda u \end{aligned}

u tiene que ser un vector propio y \lambda tiene que ser un valor propio (todos son candidatos a ser el que maximiza). ¿Pero cuál de todos ellos maximiza la inercia u' \left( \frac{1}{n} X'X \right) u?

\begin{aligned} \left( \frac{1}{n} X'X \right) u &= \lambda u \\ u' \left( \frac{1}{n} X'X \right) u &= u'\lambda u \\ u' \left( \frac{1}{n} X'X \right) u &= \lambda \\ u' \, V_X \, u = \lambda \end{aligned}

De todos los vectores candidatos, el vector propio (unitario) asociado al valor propio más grande, es el que genera la recta sobre la cual la inercia de la nube es máxima.

Sea \lambda_1 el valor propio más grande y u_1 su respectivo vector propio unitario. El vector -u_1 también es solución del problema de optimización planteado. El significado del sentido del eje se busca a partir de las variables, ya que el signo de las coordenadas depende del vector propio seleccionado.

Las coordenadas de los individuos sobre el eje generado por u_1, denominado primer eje principal, se denotan por F_1 y son: F_1 = X u_1

Ya se obtuvo la recta sobre la cual la inercia de la nube es máxima. Para obtener el plano sobre el cual la inercia de la nube es máxima, se busca una segunda recta o eje generado por un vector unitario ortogonal a u_1 que tenga la mayor inercia posible de la nube de individuos. Es decir,

\begin{aligned} {\underset {u \in \mathbb{R}^p}{\text{arg max}}}\quad & u' \left( \frac{1}{n} X'X \right) u \\ {\text{subject to}}\quad &u'u - 1 = 0. \\ & u'u_1 = 0 \end{aligned}

Usando multiplicadores de Lagrange, f(u) = u' \left( \frac{1}{n} X'X \right) u - \lambda \left( u'u - 1 \right) - \mu \left(u'u_1\right) Que tiene como primera derivada, \frac{d}{du} f(u) = 2 \left( \frac{1}{n} X'X \right) u - 2 \lambda u - \mu u_1 Igualando a cero, \begin{aligned} 2 \left( \frac{1}{n} X'X \right) u - 2 \lambda u - \mu u_1 &= 0 \\ 2 u_1' \left( \frac{1}{n} X'X \right) u - 2 \lambda u_1' u - \mu u_1' u_1 &= 0 \\ \mu &= 0 \end{aligned} de donde nos queda que, \begin{aligned} 2 \left( \frac{1}{n} X'X \right) u - 2 \lambda u &= 0 \\ \left( \frac{1}{n} X'X \right) u &= \lambda u \\ V_X \, u &= \lambda u \end{aligned} De nuevo, todos los vectores propios son candidatos. Pero el que maximiza la inercia es aquel con mayor valor propio, que además debe ser ortogonal al primer valor propio, es decir, u tendría que ser el segundo vector propio unitario (o su inverso aditivo).

Siguiendo la misma lógica, encontramos que el subespacio 3D en donde la inercia de la nube es máxima sería el generado por los tres vectores propios unitarios asociados a los tres valores propios más grandes de \frac{1}{n} X'X = V_X.

El número de valores propios diferentes de \frac{1}{n} X'X coincide con el rango de \frac{1}{n} X'X, que si n > p entonces coincide con el número de vectores columna (variables) linealmente independientes de X.

Si r = p, los p vectores propios constituyen una base ortonormal para el espacio de la nube de individuos, que permite, en orden, las proyecciones de mayor inercia.

Las n coordenadas de los individuos sobre un eje factorial s, F_s, constituyen los valores de una variable nueva denominada componente principal, F_s = X u_s Su varianza es, \begin{aligned} \frac{1}{n}\sum_{i=1}^n \left[F_s(i)\right]^2 &= \frac{1}{n}F'_s F_s \\ &= \frac{1}{n} \left( X u_s \right)' X u_s \\ &= u'_s \left( \frac{1}{n} X'X \right) u_s \\ &= \lambda_s \end{aligned}

Note que (si r = p) la inercia de la nube de individuos estandarizada (centrada y reducida) es, traza\left(\frac{1}{n} X'X\right) = p = \sum_{s=1}^p \lambda_s

# V = t(X) %*% as.matrix(X)/n = var(X)*(n-1)/n = cor(Y) 
des <- eigen(V)
lambda <- des$values
names(lambda) <- paste("lambda_", 1:p)
res <- data.frame(var = lambda, perc = 100*lambda/p)
res <- cbind(res, acum = cumsum(res$perc))
res <- rbind(res, Total = c(colSums(res[,1:2]), NA))
kable(res, digits = 2)

	var	perc	acum
lambda_ 1	2.07	68.90	68.90
lambda_ 2	0.82	27.39	96.29
lambda_ 3	0.11	3.71	100.00
Total	3.00	100.00	NA

U <- des$vectors
rownames(U) <- rownames(V)
colnames(U) <- c("Eje1","Eje2","Eje3")
kable(as.data.frame(U), digits = 3)

	Eje1	Eje2	Eje3
Color	0.579	-0.571	0.581
DA	0.673	-0.067	-0.737
EA	0.460	0.818	0.346

Las coordenadas de la nube de individuos en los nuevos ejes (en las componentes principales) se pueden obtener haciendo, F = X U en donde los vectores propios (ordenados por su valor propio correspondiente) son los vectores columna de la matriz U.

F <- as.matrix(X) %*% U
F_df <- as.data.frame(F)
kable(F_df, digits = 3)

	Eje1	Eje2	Eje3
ExCl	-0.887	-1.676	-0.106
C40M	2.679	-0.222	-0.287
C40C	1.184	0.146	0.331
C20M	1.142	-1.024	-0.346
C20C	-0.443	-0.823	0.785
ExOs	-2.469	-0.038	-0.377
O40M	0.975	1.011	0.062
O40C	0.146	1.313	-0.049
O20M	-1.040	0.645	0.107
O20C	-1.286	0.668	-0.120

Teniendo en cuenta todo lo anterior, ¿hasta ahora, para qué podríamos llegar a utilizar un análisis de componentes principales? (¿que utilidad le puedo encontrar a todo el proceso realizado con la nube de individuos?)

tpos <- rep(c("top","bottom"), length.out = n)[rank(F[,1])]
fig <- plot_ly(F_df, x = ~Eje1, y = "")
fig <- fig %>% add_markers(marker = list(symbol = 4), 
                           hovertext = rownames(F_df))
fig <- fig %>% add_text(text = rownames(F_df), 
                        textposition = tpos)
fig <- fig %>% layout(showlegend = FALSE)
fig

fig <- plot_ly(F_df, x = ~Eje1, y = ~Eje2)
fig <- fig %>% add_markers(hovertext = rownames(F_df))
fig <- fig %>% add_text(text = rownames(F_df), textposition = tpos)
fig <- fig %>% layout(showlegend = FALSE)
fig

fig <- plot_ly(F_df, x = ~Eje1, y = ~Eje2, z = ~Eje3)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(F_df))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)
fig <- fig %>% layout(showlegend = FALSE)
fig

2.1.7 Ayudas interpretación

Distancia al origen:

\begin{aligned} d^2\left(\vec{x}_i, 0\right) &= \left\|\vec{x}_i\right\|^2 \\ &= \sum_{j=1}^p x_{ij}^2 \\ &= \sum_{j=1}^p \left[ \left\langle \vec{x}_i, \vec{e}_j \right\rangle \right]^2 \\ &= \sum_{s=1}^p \left[ \left\langle \vec{x}_i, \vec{u}_s \right\rangle \right]^2 \\ &= \sum_{s=1}^p \left[ \vec{x}_i' \vec{u}_s \right]^2 \\ &= \sum_{s=1}^p \left[F_s(i)\right]^2 \end{aligned}

Contribución absoluta:

\begin{aligned} Inercia_s (N_n) = \sum_{i=1}^n p_i \left[F_s(i)\right]^2 &= \lambda_s \\ \sum_{i=1}^n \frac{p_i \left[F_s(i)\right]^2}{\lambda_s} &= 1 \\ \sum_{i=1}^n Ca_s(i) = 1 \end{aligned} donde, Ca_s(i) = \frac{p_i \left[F_s(i)\right]^2}{\lambda_s} con p_i = \frac{1}{n} cuando todos los individuos tienen el mismo peso.

Coseno cuadrado:

\begin{aligned} \cos \left(\angle_s^{\vec{x}_i}\right) &= \frac{\left\langle \vec{x}_i, \vec{u}_s \right\rangle}{\left\| \vec{x}_i \right\| \left\| \vec{u}_s \right\|} \in [-1,1] \end{aligned}

\begin{aligned} \cos^2 \left(\angle_s^{\vec{x}_i}\right) &= \frac{\left[ \left\langle \vec{x}_i, \vec{u}_s \right\rangle \right]^2}{\left\| \vec{x}_i \right\|^2} \in [0,1] \\ &= \frac{\left[F_s(i)\right]^2}{\left\| \vec{x}_i \right\|^2} \end{aligned}

\begin{aligned} \sum_{s=1}^p \cos^2 \left(\angle_s^{\vec{x}_i}\right) &= \frac{\sum_{s=1}^p \left[F_s(i)\right]^2}{\left\| \vec{x}_i \right\|^2} \\ &= \frac{\left\|\vec{x}_i\right\|^2}{\left\| \vec{x}_i \right\|^2} \\ &= 1 \end{aligned}

# tabla de ayudas para la interpretacion
# sobre el primer plano factorial
d2 <- rowSums(F^2) # distancias
cont <- 1/n*F^2 %*% diag(1/lambda)*100 # contribuciones
cos2 <- F^2/d2*100 # cosenos cuadrados
Ayu <- cbind(dis2 = d2, F1 = F[,1], F2=F[,2], 
             cont1 = cont[,1], cont2 = cont[,2], 
             cos21 = cos2[,1], cos22 = cos2[,2], 
             cosp = rowSums(cos2[,1:2]))
Ayu <- rbind(Ayu, Total = c(colSums(Ayu[,1:5]), rep(NA, 3)))
kable(Ayu, digits = 2)

	dis2	F1	F2	cont1	cont2	cos21	cos22	cosp
ExCl	3.61	-0.89	-1.68	3.80	34.19	21.80	77.89	99.69
C40M	7.31	2.68	-0.22	34.72	0.60	98.20	0.67	98.87
C40C	1.53	1.18	0.15	6.78	0.26	91.45	1.39	92.84
C20M	2.47	1.14	-1.02	6.31	12.77	52.75	42.41	95.16
C20C	1.49	-0.44	-0.82	0.95	8.23	13.20	45.42	58.62
ExOs	6.24	-2.47	-0.04	29.49	0.02	97.70	0.02	97.73
O40M	1.98	0.98	1.01	4.60	12.44	48.09	51.72	99.81
O40C	1.75	0.15	1.31	0.10	20.98	1.21	98.65	99.86
O20M	1.51	-1.04	0.65	5.24	5.07	71.67	27.58	99.25
O20C	2.12	-1.29	0.67	8.00	5.43	78.22	21.10	99.32
Total	30.00	0.00	0.00	100.00	100.00	NA	NA	NA

fig <- plot_ly(F_df, x = ~Eje1, y = ~Eje2, z = ~Eje3)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(F_df))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)
fig <- fig %>% layout(showlegend = FALSE)
fig

2.1.8 Individuos suplementarios

Adicionalmente, en los ejes factoriales se pueden representar:

Individuos que no participaron en la obtención de los ejes (individuos nuevos)

F_s(i^{+}) = \left\langle \vec{x}_{i^+}, \vec{u}_s \right\rangle = \vec{x}'_{i^{+}} \vec{u}_s
Centro de gravedad de un grupo de individuos, por ejemplo un grupo dado por la categoría de una variable categórica (el valor de una variable cualitativa). Equivalente al centro de gravedad de las coordenadas factoriales de los individuos que pertenecen al grupo.

comer <- as.matrix(cafe[11:12,1:3])
comc <- comer - rep(1,2) %*% t(g) # centrado
comcr <- comc %*% solve(Dsigma) # reducido
colnames(comcr) <- colnames(comer)
Fsup <- comcr %*% U
# primer plano factorial
plot(F[,1:2], las = 1, asp = 1, bty = "n") 
text(F[,1:2], label = rownames(F), col = "black", pos = 4)
abline(h = 0, v = 0, col = "darkgrey")
points(Fsup, col="black", pch=20)  # cafes comerciales
text(Fsup, labels=c("Com1","Com2"), col="darkgreen", pos = 2)
conta <- factor(c("exce","maiz","ceba","maiz","ceba",
                  "exce","maiz","ceba","maiz","ceba"))
Fconta <- centroids(F, conta)$centroids
points(Fconta, col = "brown", pch = 20)
text(Fconta, col = "brown", labels = rownames(Fconta), pos = 2)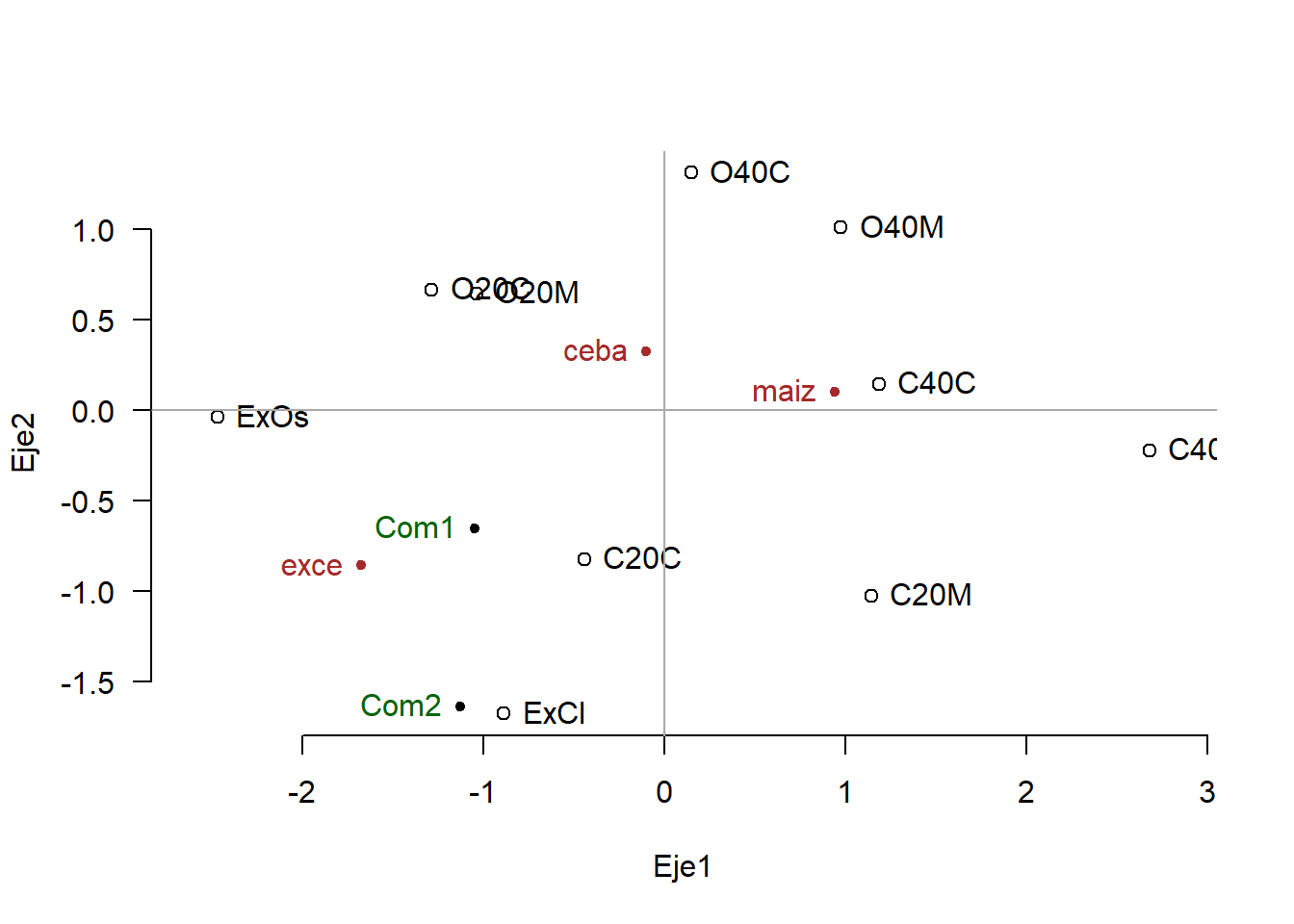

Para los centros de gravedad de las categorías se puede calcular la distancia al origen y los cosenos cuadrados, pero las contribuciones absolutas son cero porque no participan en la obtención de los ejes factoriales.

Adicionalmente, se puede hacer un análisis descriptivo bivariado entre las categorías (variable categórica) y cada uno de los ejes factoriales (variable cuantitativa). Recordemos que la media de un componente principal es cero porque es centrado \left(\mu = 0\right) y su varianza es su valor propio asociado \left(\sigma^2 = \lambda_s\right). Entonces, el valor test para una categoría k, asumida por n_k, estaría dada por, \begin{aligned} \frac{F_s(k) - \mu}{\sigma_k} &= \sqrt{\frac{(n - 1)n_k}{n - n_k}} \frac{F_s(k) - \mu}{\sigma} \\ &= \sqrt{\frac{(n - 1)n_k}{\left(n - n_k\right)\lambda_s}} F_s(k) \end{aligned}

2.2 La nube de variables

Cada punto corresponderá a un vector columna y representará a una variable en un espacio de tantas dimensiones como individuos.

kable(cafe[1:3 ,1:9], digits = 2)

	Color	DA	EA	pH	AcidezT	Cafeina	AcidosCl	D2325	D2272
ExCl	298	385.1	25	5.02	11.7	1.40	2.74	-0.10	-0.06
C40M	361	481.3	41	5.11	6.5	0.81	1.62	-0.06	-0.04
C40C	321	422.6	40	5.12	5.8	0.80	1.61	-0.06	-0.04

tAux = as.data.frame(t(cafe[1:3 ,1:9]))
fig <- plot_ly(tAux, x = ~ExCl, y = ~C40M, z = ~C40C)
fig <- fig %>% add_markers()
fig <- fig %>% add_text(text = rownames(tAux))
fig <- fig %>% layout(title = "vectores columna\n(variables)",
                      showlegend = FALSE)
fig

Sea \vec{y}_j, \vec{y_C}_j y \vec{x}_j el j-ésimo vector columna, respectivamente, de las matrices Y, Y_C y X.

Por otra parte, nos será de mucha utilidad el producto interno dado por la matriz \frac{1}{n} I_n, \left\langle \vec{u}, \vec{v} \right\rangle_{\frac{1}{n} I_n} = \vec{u}' \left( \frac{1}{n} I_n \right) \vec{v}

Note que, \begin{aligned} \left\|\vec{1}_n \right\|^2_{\frac{1}{n} I_n} &= \left\langle \vec{1}_n, \vec{1}_n \right\rangle_{\frac{1}{n} I_n} \\ &= \vec{1}_n' \left( \frac{1}{n} I_n \right) \vec{1}_n \\ &= \frac{1}{n} \vec{1}_n' \vec{1}_n \\ &= \frac{1}{n} \sum_{i=1}^n 1^2 \\ &= \frac{1}{n} n \\ &= 1 \end{aligned} es decir, \vec{1}_n es un vector unitario (para el producto interno dado por \frac{1}{n} I_n).

2.2.1 Significado de la media

\begin{aligned} \bar{y}_j &= \frac{1}{n} \sum_{i=1}^n y_{ij} \\ &= \frac{1}{n} \sum_{i=1}^n (y_{ij})(1) \\ &= \frac{1}{n} \vec{y}_j' \vec{1}_n \\ &= \vec{y}_j' \left( \frac{1}{n} I_n \right) \vec{1}_n \\ &= \left\langle \vec{y}_j \, , \, \vec{1}_n \right\rangle_{\frac{1}{n} I_n} \end{aligned} La media de las componentes de la j-ésima variable es la proyección del vector columna sobre la recta que genera el vector unitario \vec{1}_n.

2.2.2 Significado del centrado

Sea \vec{\bar{y}}_j un vector en donde sus n componentes son iguales a \bar{y}_j, entonces \vec{\bar{y}}_j = \bar{y}_j \vec{1}_n y, {\vec{y}_{C}}_j = \vec{y}_j - \vec{\bar{y}}_j Lo que quiere decir que una variable centrada es la proyección de la variable sobre el subespacio ortogonal a la recta generada por \vec{1}_n; subespacio que naturalmente es de una dimensión menos que el de la variable sin centrar.

2.2.3 Significado de las varianzas y covarianzas

\begin{aligned} \sigma_{jk} = cov\left( \vec{y}_j \, , \, \vec{y}_k \right) &= \frac{1}{n}\sum_{i=1}^n \left(y_{ij} - \bar{y}_j \right) \left(y_{ik} - \bar{y}_j\right) \\ &= \left\langle {\vec{y}_{C}}_j \, , \, {\vec{y}_{C}}_k \right\rangle_{\frac{1}{n} I_n} \end{aligned} de donde, \begin{aligned} \sigma^2_{j} = var\left( \vec{y}_j \right) &= \frac{1}{n}\sum_{i=1}^n \left( y_{ij} - \bar{y}_j \right)^2 \\ &= \left\langle {\vec{y}_{C}}_j \, , \, {\vec{y}_{C}}_j \right\rangle_{\frac{1}{n} I_n} \\ &= \left\| {\vec{y}_{C}}_j \right\|^2_{\frac{1}{n} I_n} \end{aligned} La covarianza es el producto interno entre vectores columna y la varianza es la norma al cuadrado del vector columna (la desviación estándar es la norma).

2.2.4 Significado de la reducción

\begin{aligned} \vec{x}_j &= \frac{\vec{y}_j - \vec{\bar{y}}_j}{\sigma_j} \\ &= \frac{{\vec{y}_{C}}_j}{\left\| {\vec{y}_{C}}_j \right\|} \end{aligned} Un vector columna después del centrado y reducido es un vector unitario \left\| \vec{x}_j \right\| = 1.

2.2.5 Significado de la correlación

\begin{aligned} \rho_{jk} = cor\left( \vec{y}_j \, , \, \vec{y}_k \right) &= \frac{\sigma_{jk}}{\sigma_{j} \sigma_{k}} \\ &= \frac{\left\langle {\vec{y}_{C}}_j \, , \, {\vec{y}_{C}}_k \right\rangle_{\frac{1}{n} I_n}}{\left\| {\vec{y}_{C}}_j \right\|_{\frac{1}{n} I_n} \left\| {\vec{y}_{C}}_k \right\|_{\frac{1}{n} I_n}} \\ &= \cos\left(\angle_{{\vec{y}_{C}}_j}^{{\vec{y}_{C}}_k}\right) \\ &= \cos\left(\angle_{\vec{x}_j}^{\vec{x}_k}\right) \end{aligned}

Concluimos que la nube de variables, luego del centrado y el reducido, es una representación de la matriz de correlaciones. Por ejemplo, vectores columna ortogonales/perpendiculares indican que las respectivas variables no están correlacionadas.

2.2.6 Inercia

\begin{aligned} Inercia(N_p) &= \sum_{j=1}^{p} m_j \, d^2_{\frac{1}{n} I_n}\left(\vec{y}_{Ci} ,\vec{0}\right) \end{aligned}

Cuando todos los m_j son iguales a 1, \begin{aligned} Inercia(N_p) &= \sum_{j=1}^{p} m_j \, d^2_{\frac{1}{n} I_n}\left(\vec{y}_{Ci} ,\vec{0}\right) \\&= \sum_{j=1}^{p} \left\| {\vec{y}_{C}}_j \right\|^2_{\frac{1}{n} I_n} \\ &= \sum_{j=1}^{p}var\left( \vec{y}_j \right) \\ &= \sum_{j=1}^{p} \sigma_j^2 \end{aligned}

La contribución del vector columna a la inercia de la nube de variables es la varianza de la variable correspondiente. En el caso normado (centrado y reducido) cada variable aporta 1 a la inercia y la inercia total es igual al número de variables.

2.2.7 Nuevos ejes

La proyección de una variable \vec{x}_j sobre una recta generada por el vector v (\frac{1}{n} I_n unitario) en \mathbb{R}^n es, \begin{aligned} \left\langle \vec{x}_j \, , \, \vec{v} \right\rangle_{\frac{1}{n} I_n} &= \vec{x}_j' \left( \frac{1}{n} I_n \right) \vec{v} \\ &= \frac{1}{n} \vec{x}_j' \vec{v} \end{aligned}

La inercia de las p variables proyectadas es, \begin{aligned} \sum_{j=1}^p \left( \frac{1}{n} \vec{x}_j' \vec{v} \right)^2 &= \frac{1}{n^2} \left( X \vec{v} \right)'\left( X \vec{v} \right) \\ &= \frac{1}{n^2} \vec{v}' X X' \vec{v} \\ &= \frac{1}{n} \left[ \vec{v}' \left( \frac{1}{n} X X' \right) \vec{v} \right] \end{aligned}

El eje de mayor inercia proyectada se encuentra solucionando, \begin{aligned} {\underset {v \in \mathbb{R}^n}{\text{arg max}}}\quad & \frac{1}{n} \left[ \vec{v}' \left( \frac{1}{n} X X' \right) \vec{v} \right] \\ {\text{subject to}}\quad &\vec{v}' \left( \frac{1}{n} I_n \right) \vec{v} - 1 = 0. \end{aligned}

Usando multiplicadores de Lagrange, f(u) = \frac{1}{n} \left[ \vec{v}' \left( \frac{1}{n} X X' \right) \vec{v} \right] - \mu \left( \frac{1}{n} \vec{v}' \vec{v} - 1 \right) que tiene como primera derivada, \frac{d}{du} f(u) = \frac{2}{n} \left[ \left( \frac{1}{n} X X' \right) v \right] - \frac{2}{n} \mu v Igualando a cero, \begin{aligned} \frac{2}{n} \left[ \left( \frac{1}{n} X X' \right) v \right] - \frac{2}{n} \mu v &= 0 \\ \left( \frac{1}{n} X X' \right) v &= \mu v \end{aligned} De donde concluimos que la solución está dada por el vector propio (o su inverso aditivo) asociado al mayor valor propio de la matriz \frac{1}{n} X X'. Sin embargo, los valores propios mayores que cero de \frac{1}{n} X' X y \frac{1}{n} X X' son iguales.

La coordenada sobre un eje s de la variable j, se obtiene mediante, G_s(j) = \frac{1}{n} \vec{x}_j' v_s

2.2.8 Relación entre las dos nubes (espacios)

La matriz \frac{1}{n} XX' tiene p valores propios, que son iguales a los valores propios de \frac{1}{n} X'X y los restantes n - p valores propios son 0.
El vector coordenadas de los n individuos sobre el eje s, F_s, es un vector propio de \frac{1}{n} XX'.
La varianza de F_s es \lambda_s, y por lo tanto, el vector propio v_s se puede calcular mediante: v_s = \frac{1}{\sqrt{\lambda_s}} F_s.
G_s, vector de coordenadas de las p variables sobre el eje s, es un vector propio de \frac{1}{n} X'X.
La varianza de G_s es \lambda_s, y por lo tanto, se puede obtener mediante: G_s = \sqrt{\lambda_s} u_s.
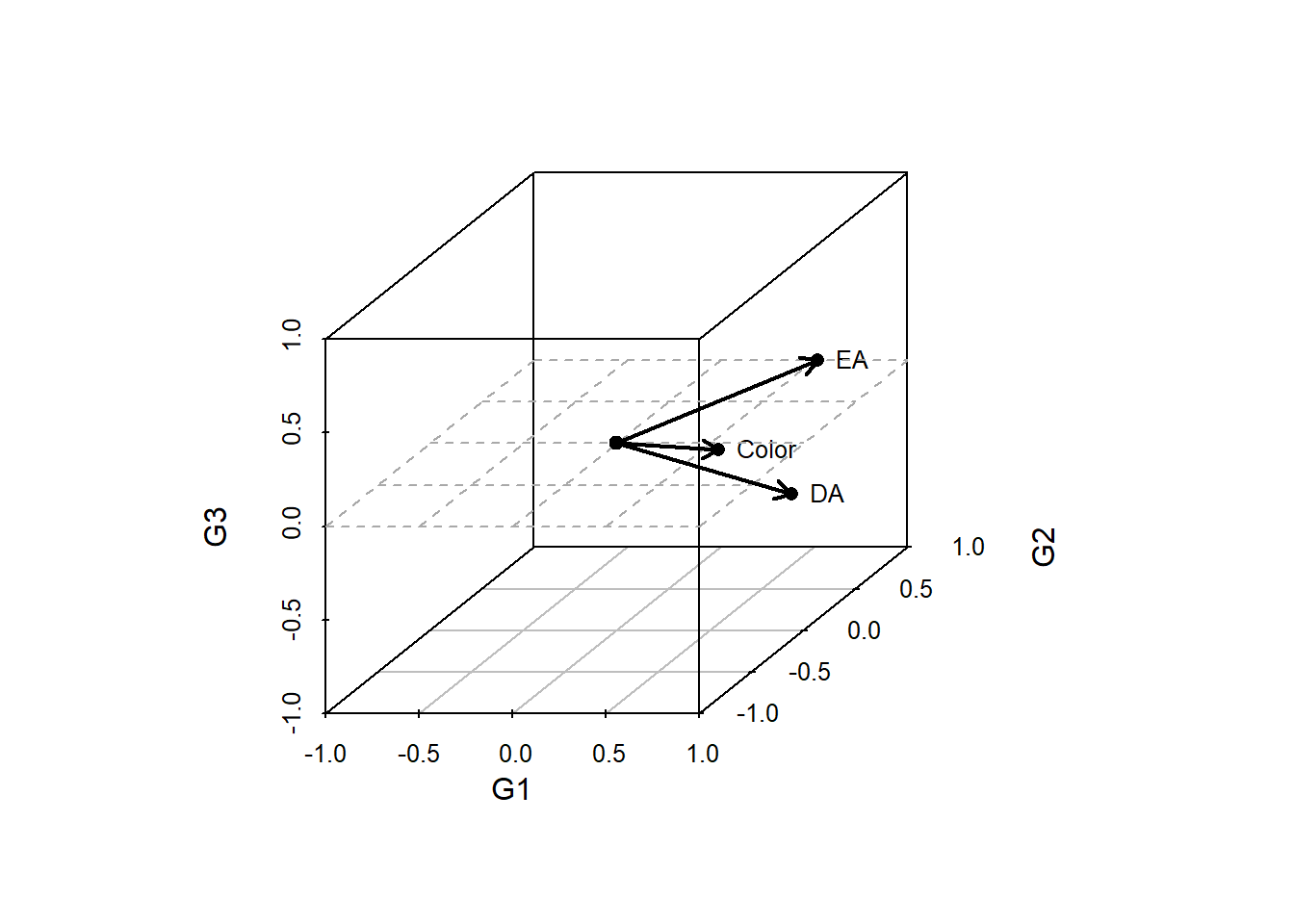
En el ACP normado, las coordenadas de G_s son las correlaciones entre las variables y el eje s.

G <- U %*% diag(sqrt(lambda))
colnames(G)<-c("G1","G2","G3");
kable(as.data.frame(G), digits = 3)

	G1	G2	G3
Color	0.833	-0.518	0.194
DA	0.967	-0.061	-0.246
EA	0.661	0.741	0.115

kable(as.data.frame(cor(Y,F)), digits = 3)

	Eje1	Eje2	Eje3
Color	0.833	-0.518	0.194
DA	0.967	-0.061	-0.246
EA	0.661	0.741	0.115

G3D <- scatterplot3d(G, pch = 16, color = "black", 
                     xlim = c(-1,1), ylim = c(-1,1), 
                     zlim = c(-1,1), asp = 1)
coord <- G3D$xyz.convert(G)
text(coord, labels = rownames(G), 
     cex = 0.8, col = "black", pos = 4)
G3D$plane(0, 0, 0, col="darkgrey")
G3D$points3d(t(c(0,0,0)), pch = 19, col = "black")
cero <- G3D$xyz.convert(0,0,0)
for(eje in 1:3){
  arrows(cero$x, cero$y, coord$x[eje], coord$y[eje], 
         lwd = 2, length = 0.1, col = "black")
}

# Código experimental
G_df = as.data.frame(G)
fig <- plot_ly(G_df, x = ~G1, y = ~G3, z = ~G2)
# Graficare como puntos pero sería mejor como flechas
fig <- fig %>% add_markers() 
fig <- fig %>% add_text(text = rownames(G_df))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)

sphere <- function(n = 100){
  theta <- seq(0, pi, length.out = n)
  phi <- seq(0, 2 * pi, length.out = n)
  r <- 1
  x <- r * outer(sin(theta), cos(phi))
  y <- r * outer(sin(theta), sin(phi))
  z <- r * outer(cos(theta), rep(1, length(phi)))
  return(list(x = x, y = y, z = z))
}
s_c <- sphere()
fig <- fig %>% add_trace(x = s_c$x, y = s_c$y, z = s_c$z, 
                         type = 'surface', opacity = 0.2, 
                         colorscale = "Greys", # cambiar por valor fijo
                         showscale = FALSE)

fig <- fig %>% layout(title = "vectores columna\n(variables)",
                      scene = list(xaxis = list(range = c(-1,1)),
                                   yaxis = list(range = c(-1,1)),
                                   zaxis = list(range = c(-1,1)),
                                   aspectratio = list(x=1,y=1,z=1),
                                   camera = list(eye = list(x=1,y=1,z=1))),
                      showlegend = FALSE)
fig

2.2.9 Ayudas interpretación

De manera equivalente a como se hizo para los individuos, para las variables también se pueden calcular contribuciones absolutas y cosenos cuadrados. En el caso del ACP normado, la distancia al origen de cada una de las variables siempre es igual a 1.

# Primer plano factorial
s.corcircle(G)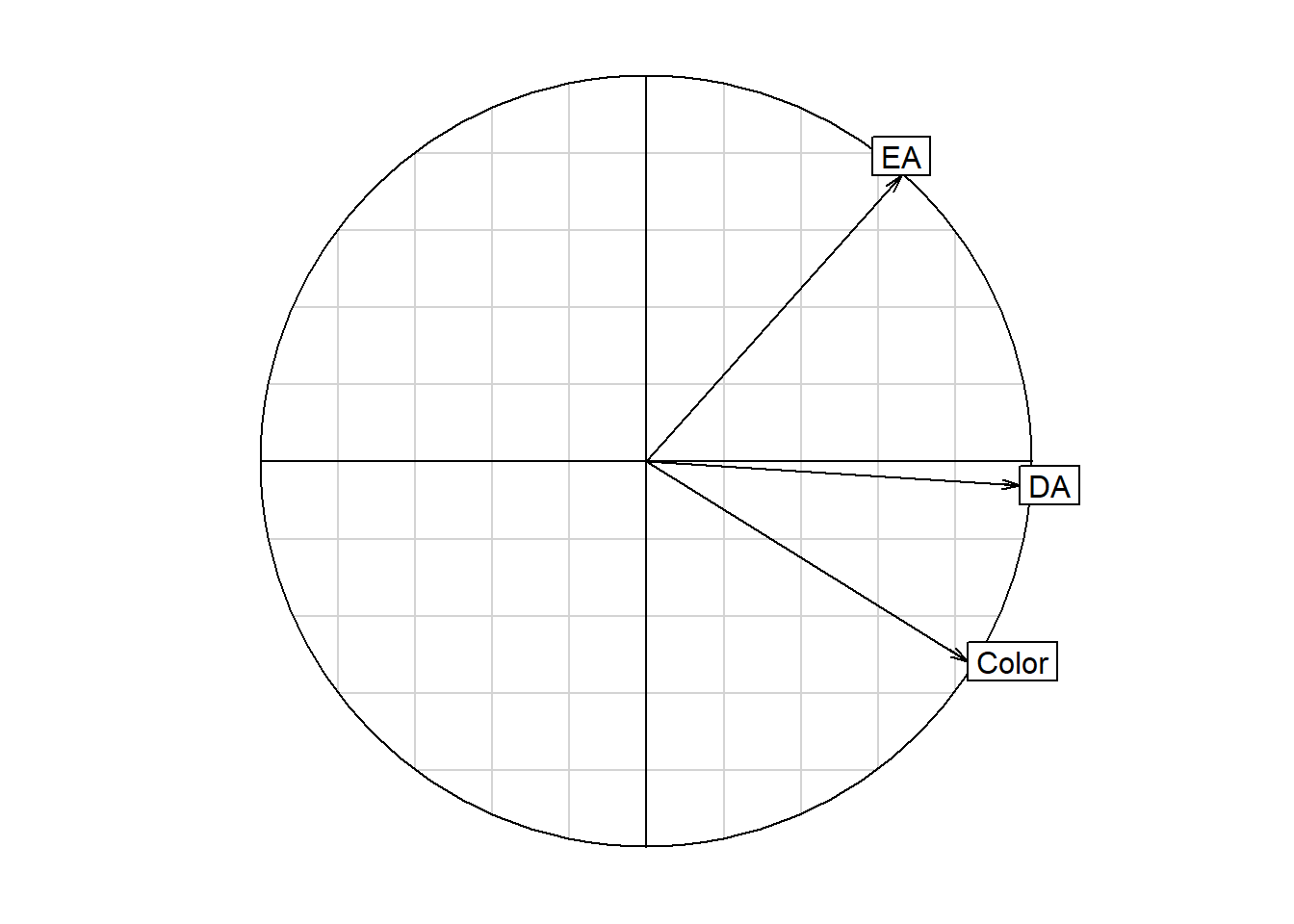

kable(as.data.frame(V), digits = 2)

	Color	DA	EA
Color	1.00	0.79	0.19
DA	0.79	1.00	0.57
EA	0.19	0.57	1.00

2.2.10 Variables continuas suplementarias

Sobre los ejes principales se pueden proyectar variables que no participaron en el análisis. Igual que como ocurre para las demás variables, cada coordenada es la correlación entre la variable y cada eje.

En el ejemplo “Café” se proyecta la nota de impresión global dada por un panel de catadores para explorar su relación con las tres variables físicas en conjunto.

s.corcircle(G)
# proyeccion de nota como variable ilustrativa
Impresion <- cafe[1:10,16]
FImpresion <- cor(Impresion, F)
arrows(0, 0, FImpresion[1], FImpresion[2], 
       col = "black", angle = 10, lty = 3)
text(FImpresion, "Impresion", col="black",
     pos = 1, font = 3)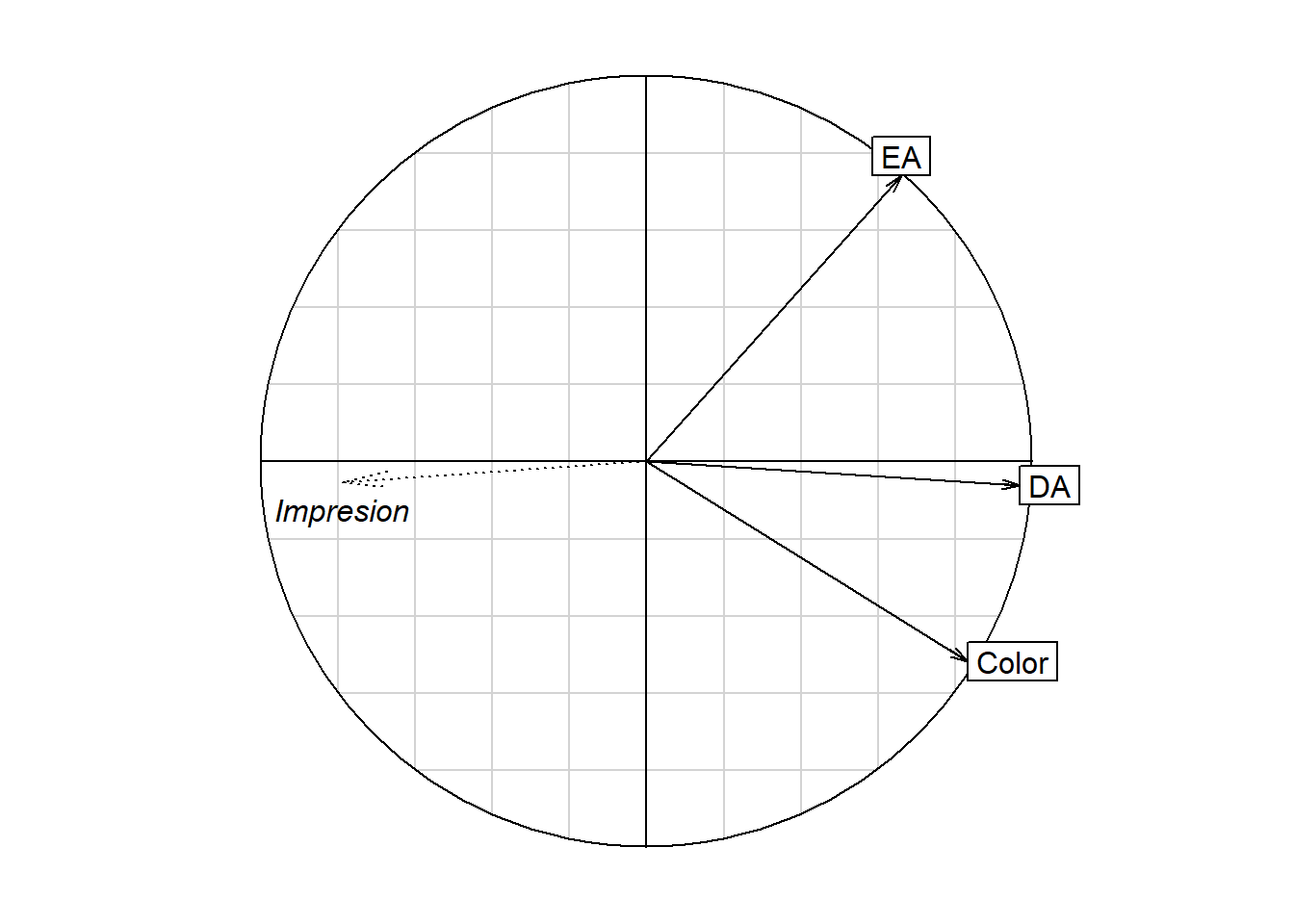

2.3 ACP con ade4 y FactoClass

Función	Librería	Descripción
`dudi.pca`	`ade4`	ACP, por defecto normado.
`inertia.dudi`	`ade4`	Ayudas para la interpretación, por defecto solo valores propios.
`s.corcircle`	`ade4`	Círculos de correlaciones.
`plotcc`	`FactoClass`	Círculos de correlaciones con `ggplot2`.
`s.arrow`	`ade4`	Planos factoriales de las variables, en un ACP no normado.
`s.label`	`ade4`	Planos factoriales de los individuos.
`plot.dudi`	`FactoClass`	Planos factoriales de los individuos, usando el parámetro `Tcol = FALSE`.
`suprow`	`ade4`	Coordenadas de individuos suplementarios.
`points`	`graphics`	Proyectar puntos en un gráfico.
`text`	`graphics`	Poner etiquetas asociadas a los puntos en un gráfico.
`cor(acp$li,Xsup)`	`stats`	Correlaciones entre variables suplementarias y ejes (coordenadas en un ACP normado. Si `ACP` es el objeto de salida del ACP y `Xsup` es la tabla de variables suplementarias.
`arrows`	`graphics`	Proyectar variables ilustrativas sobre un círculo de correlaciones.
`supqual`	`FactoClass`	Coordenadas y ayudas a la interpretación de variables cualitativas ilustrativas.
`s.class`	`ade4`	Planos factoriales de los individuos destacando las clases de una partición definida por una variable cualitativa.

# ACP normado con variables físicas y reteniendo dos ejes
acp <- dudi.pca(cafe[1:10,1:3], scannf=FALSE)
acp$cent          # medias de las variables:

Color    DA    EA 
276.7 401.2  35.5

round(acp$norm, 2) # desviación estándar de las variables

Color    DA    EA 
55.73 39.50  5.78

inertia(acp)      # valores propios y porcentajes

Inertia information:
Call: inertia.dudi(x = acp)

Decomposition of total inertia:
    inertia     cum  cum(%)
Ax1  2.0670   2.067   68.90
Ax2  0.8216   2.889   96.29
Ax3  0.1113   3.000  100.00

barplot(acp$eig)  # histograma de valores propios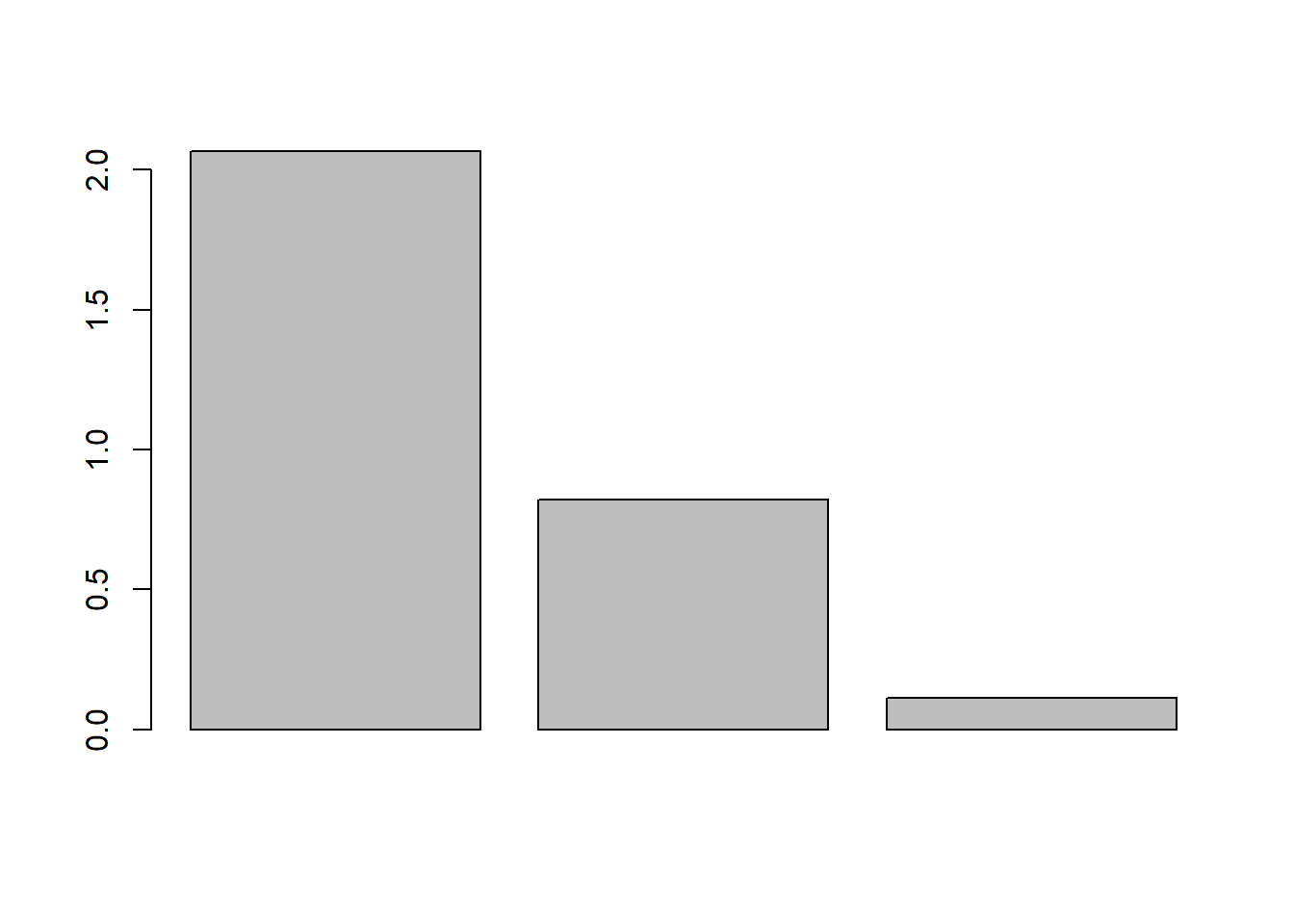

round(acp$c1, 3)   # vectores propios

        CS1    CS2
Color 0.579 -0.571
DA    0.673 -0.067
EA    0.460  0.818

Código

fviz_screeplot(acp, addlabels = TRUE, 
               ylim = c(0, 100))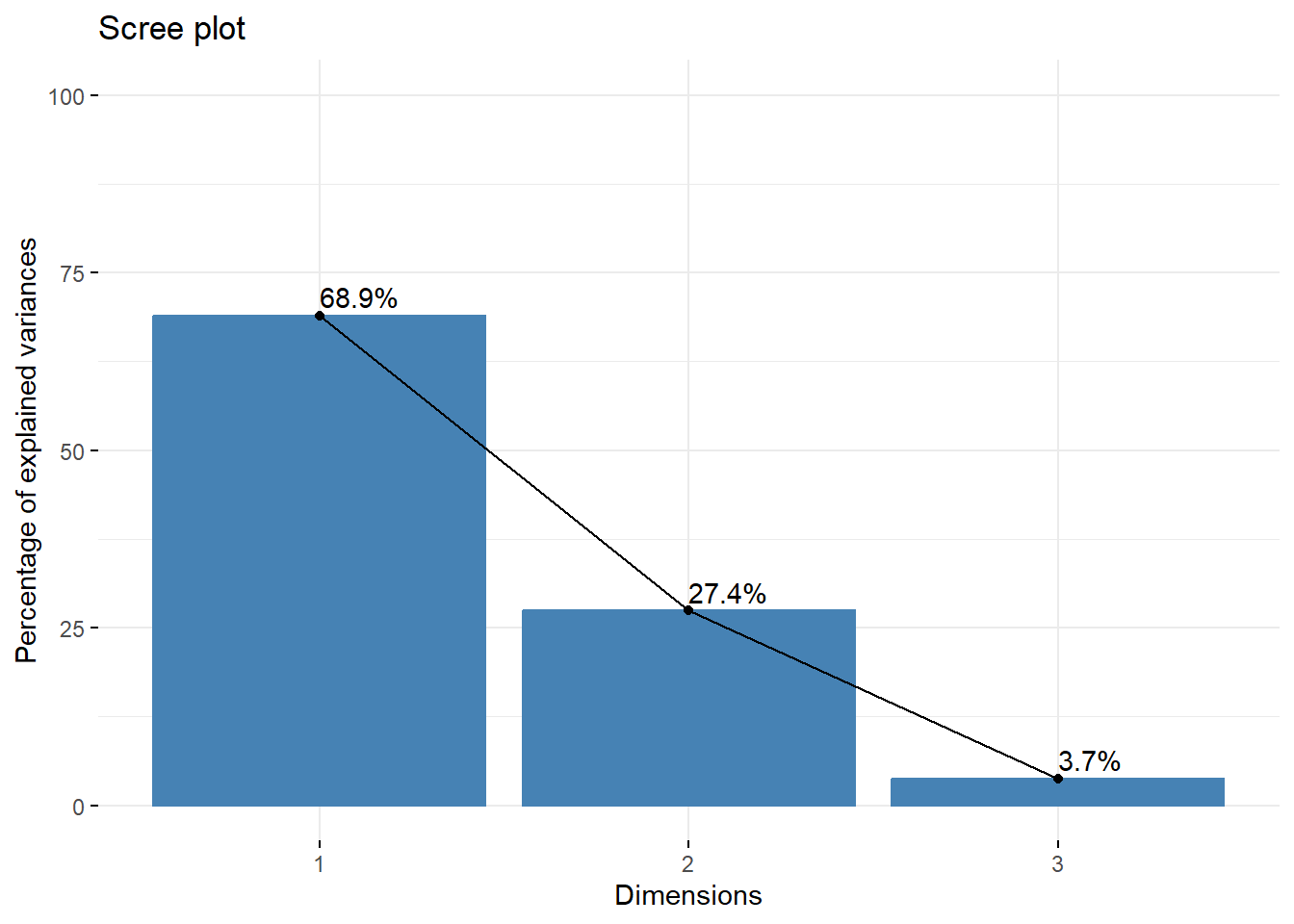

s.corcircle(acp$co)
# proyeccion de la variable Impresion como ilustrativa
(coimpre <- cor(cafe[1:10,16], acp$li))

       Axis1    Axis2
[1,] -0.7887 -0.05268

s.arrow(coimpre, label="Impresion", 
        add.plot = TRUE, boxes = FALSE)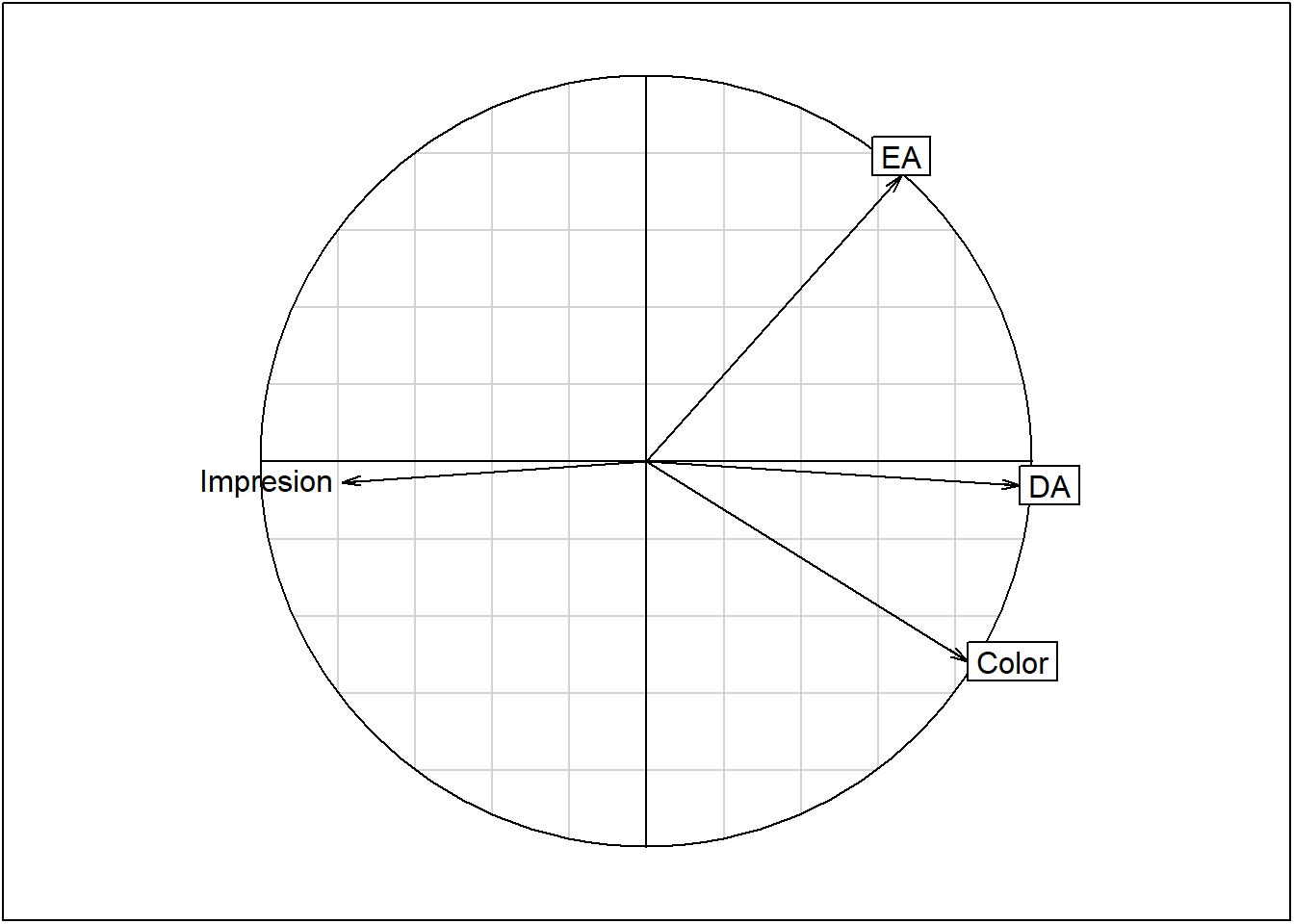

# coordenadas de las variables = correlaciones con los ejes
round(acp$co, 3)

      Comp1  Comp2
Color 0.833 -0.518
DA    0.967 -0.061
EA    0.661  0.741

# ayudas para la interpretación de las variables  
inertia(acp, , TRUE)

Inertia information:
Call: inertia.dudi(x = acp, col.inertia = TRUE)

Decomposition of total inertia:
    inertia     cum  cum(%)
Ax1  2.0670   2.067   68.90
Ax2  0.8216   2.889   96.29
Ax3  0.1113   3.000  100.00

Column contributions (%):
  Color      DA      EA 
  33.33   33.33   33.33 

Column absolute contributions (%):
        Axis1   Axis2
Color   33.58 32.6507
DA      45.28  0.4463
EA      21.14 66.9029

Signed column relative contributions:
        Axis1    Axis2
Color   69.41 -26.8274
DA      93.59  -0.3667
EA      43.70  54.9706

Cumulative sum of column relative contributions (%):
        Axis1 Axis1:2 Axis3:3
Color   69.41   96.24   3.759
DA      93.59   93.96   6.042
EA      43.70   98.67   1.331

fig <- fviz_pca_var(acp, col.var = "black")
coord <- cor(cafe[1:10,16], F)
rownames(coord) <- "Impresión"
fviz_add(fig, coord, color ="blue", geom="arrow", labelsize=3)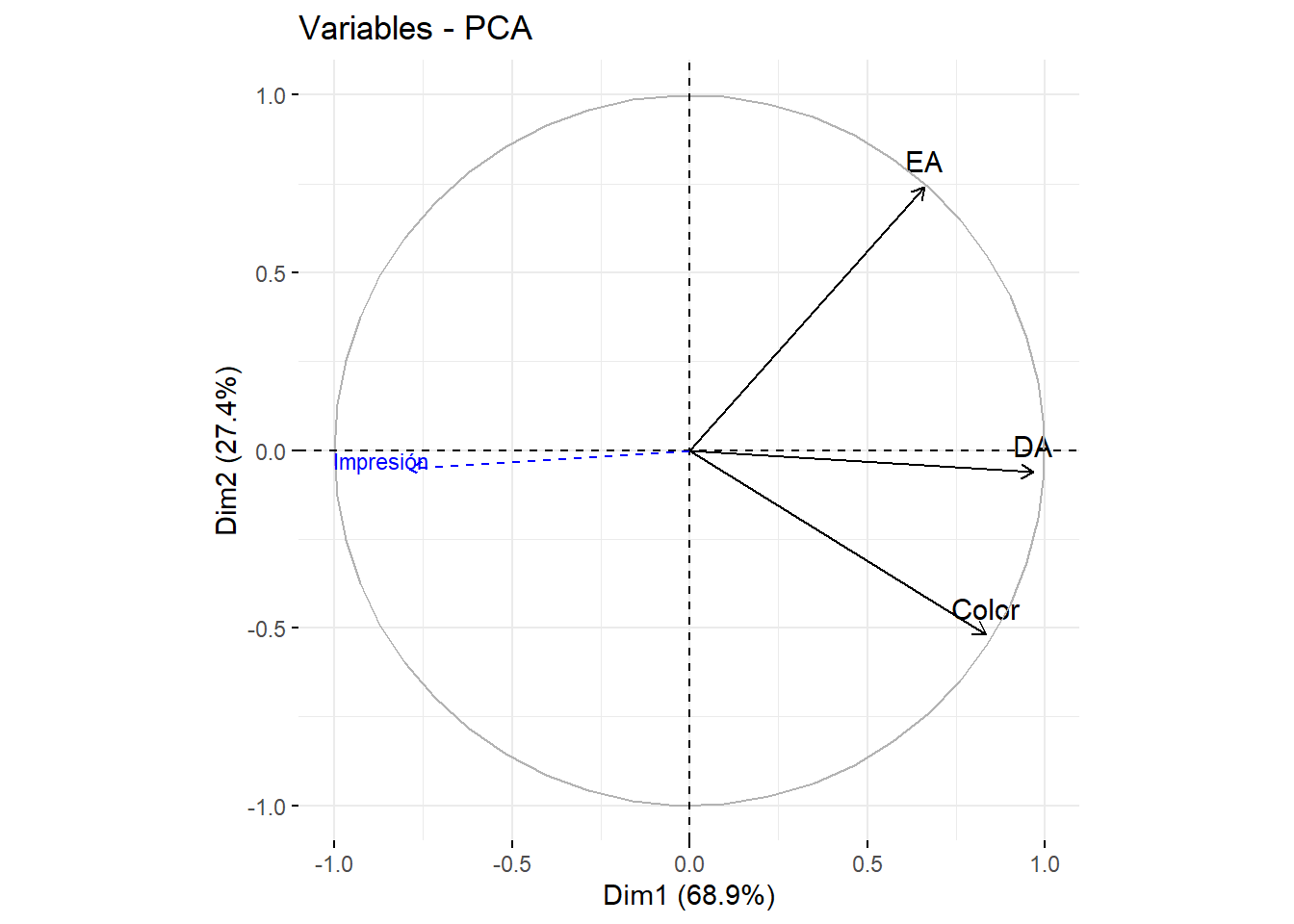

Primer plano factorial de las variables, más nota de impresión global de los catadores (variable suplementaria proyectada)

plot(acp, Tcol = FALSE, gg = TRUE)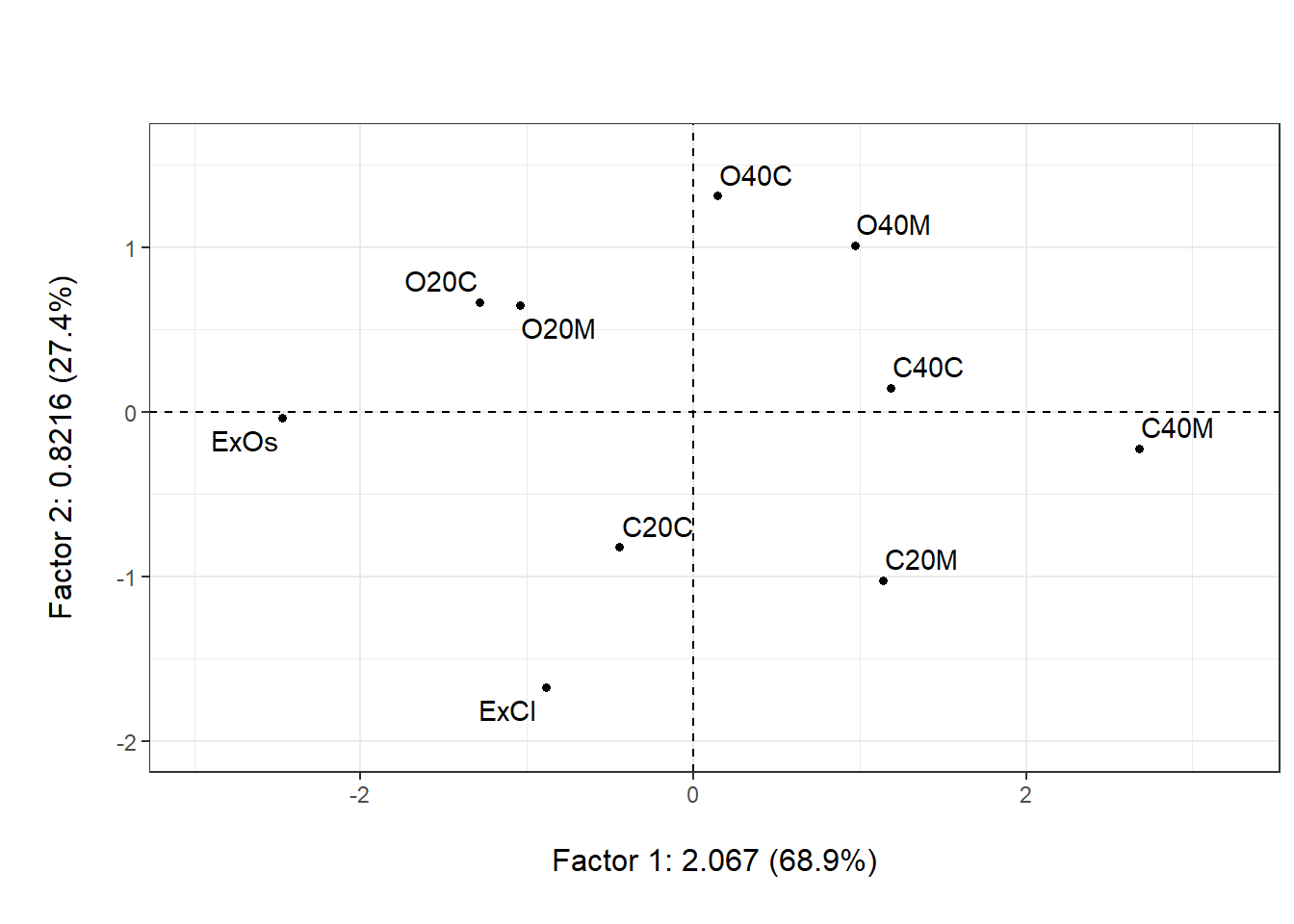

round(acp$li, 2)   # coordenadas de los cafés

     Axis1 Axis2
ExCl -0.89 -1.68
C40M  2.68 -0.22
C40C  1.18  0.15
C20M  1.14 -1.02
C20C -0.44 -0.82
ExOs -2.47 -0.04
O40M  0.98  1.01
O40C  0.15  1.31
O20M -1.04  0.65
O20C -1.29  0.67

inertia(acp, TRUE) # ayudas para la interpretación de los cafés

Inertia information:
Call: inertia.dudi(x = acp, row.inertia = TRUE)

Decomposition of total inertia:
    inertia     cum  cum(%)
Ax1  2.0670   2.067   68.90
Ax2  0.8216   2.889   96.29
Ax3  0.1113   3.000  100.00

Row contributions (%):
   ExCl    C40M    C40C    C20M    C20C    ExOs    O40M    O40C    O20M    O20C 
 12.025  24.363   5.106   8.247   4.965  20.794   6.589   5.825   5.035   7.051 

Row absolute contributions (%):
       Axis1    Axis2
ExCl  3.8050 34.19476
C40M 34.7227  0.60012
C40C  6.7777  0.25918
C20M  6.3136 12.76906
C20C  0.9510  8.23410
ExOs 29.4872  0.01798
O40M  4.5990 12.44216
O40C  0.1027 20.98013
O20M  5.2368  5.07039
O20C  8.0044  5.43211

Signed row relative contributions:
       Axis1     Axis2
ExCl -21.803 -77.88530
C40M  98.199  -0.67464
C40C  91.455   1.39017
C20M  52.749 -42.40673
C20C -13.197 -45.42087
ExOs -97.704  -0.02368
O40M  48.090  51.71557
O40C   1.214  98.64686
O20M -71.665  27.58164
O20C -78.219  21.10044

Cumulative sum of row relative contributions (%):
       Axis1 Axis1:2 Axis3:3
ExCl  21.803   99.69  0.3122
C40M  98.199   98.87  1.1262
C40C  91.455   92.84  7.1552
C20M  52.749   95.16  4.8442
C20C  13.197   58.62 41.3821
ExOs  97.704   97.73  2.2724
O40M  48.090   99.81  0.1949
O40C   1.214   99.86  0.1387
O20M  71.665   99.25  0.7532
O20C  78.219   99.32  0.6803

lcom <- suprow(acp, cafe[11:12,1:3])$lisup
plot(acp, Tcol = FALSE) 
points(lcom, col = "darkgreen")
text(lcom, rownames(lcom), col = "darkgreen", pos = 2)
# proyección variables conta (contaminación) como ilustrativa
conta<-factor(c("exce","maiz","ceba","maiz","ceba",
                "exce","maiz","ceba","maiz","ceba"))
supconta <- supqual(acp, conta)
points(supconta$coor, col = "red", pch = 20)
text(supconta$coor, rownames(supconta$coor), 
     col = "red", pos = 2)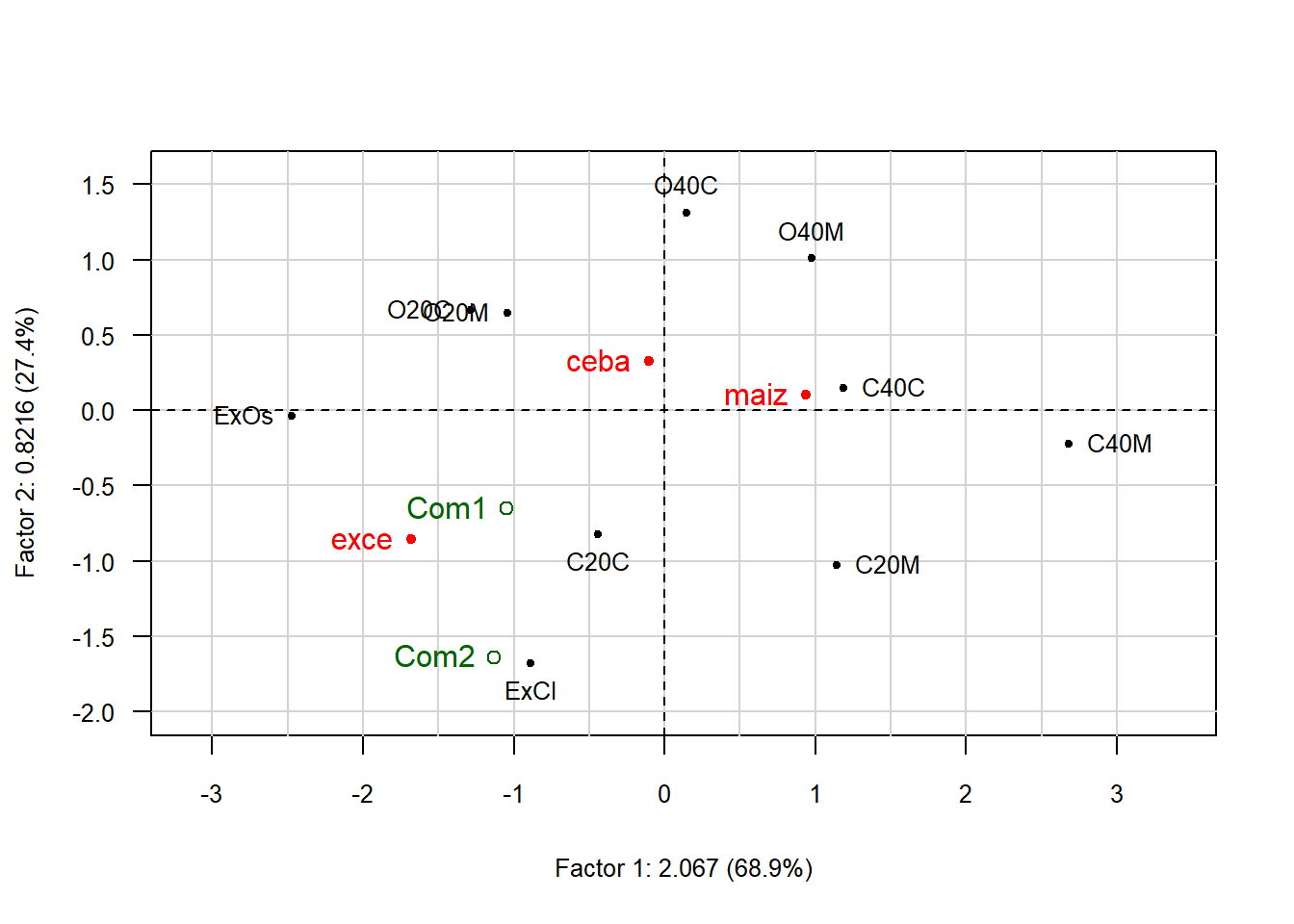

round(supconta$tv, 2); # valores test de categorías de conta

     Axis1 Axis2
ceba -0.17  0.88
exce -1.75 -1.42
maiz  1.60  0.28

plot(acp, Tcol = FALSE)
ade4::s.class(acp$li, conta, col = c("orange","darkgreen","red"),
              add.plot = TRUE, cellipse = 0, clabel = 0.5)
lcom <- suprow(acp, cafe[11:12,1:3])$lisup
points(lcom, col = "blue", pch = 16, cex = .8)
text(lcom, rownames(lcom), col = "blue", pos = 2, cex = .8)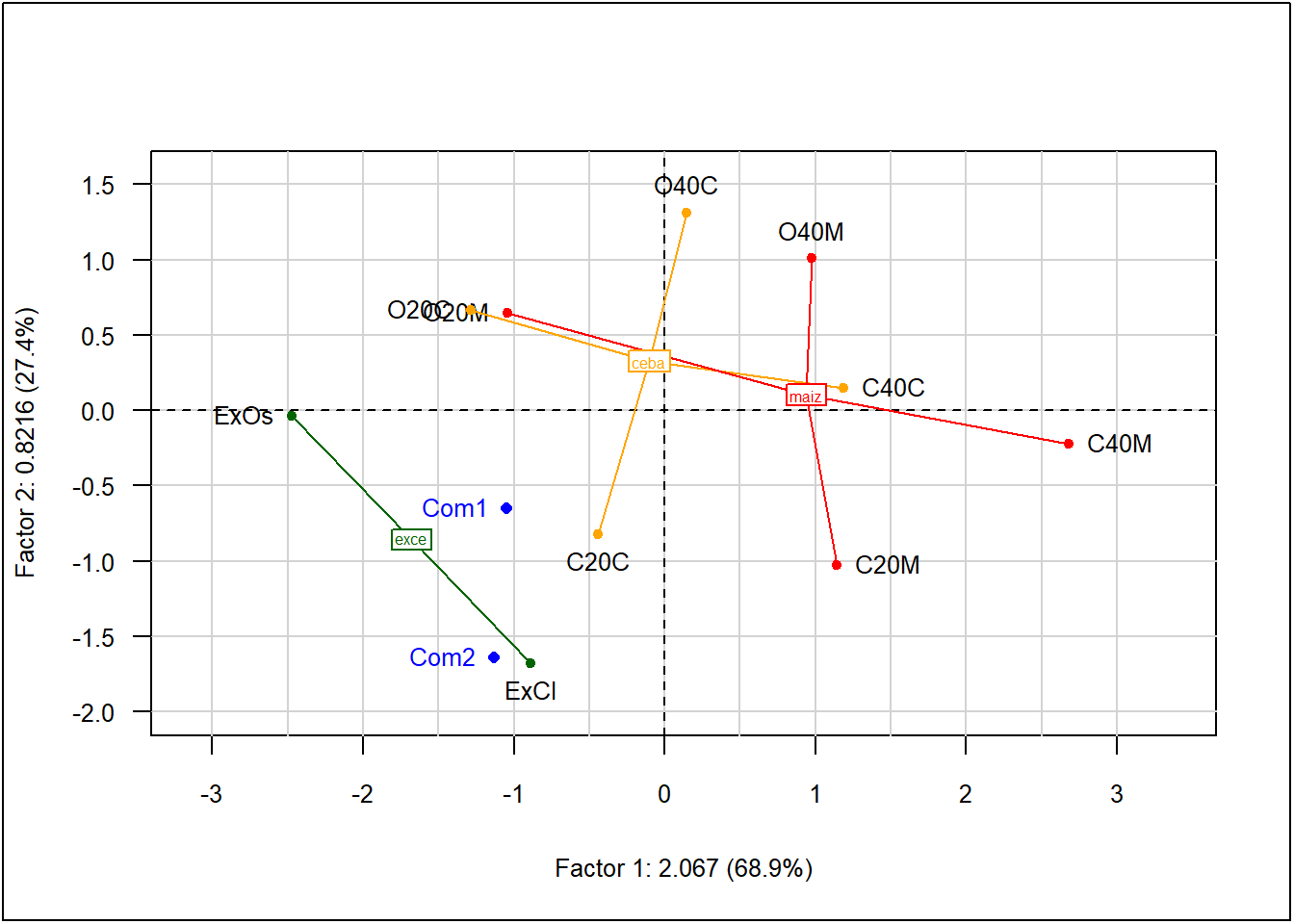

Podemos unir en un solo gráfico:

fig <- fviz_pca_biplot(acp, repel = TRUE)
fig <- fviz_add(fig, coord, color ="blue", geom="arrow")
fviz_add(fig, lcom, color ="purple", geom="point")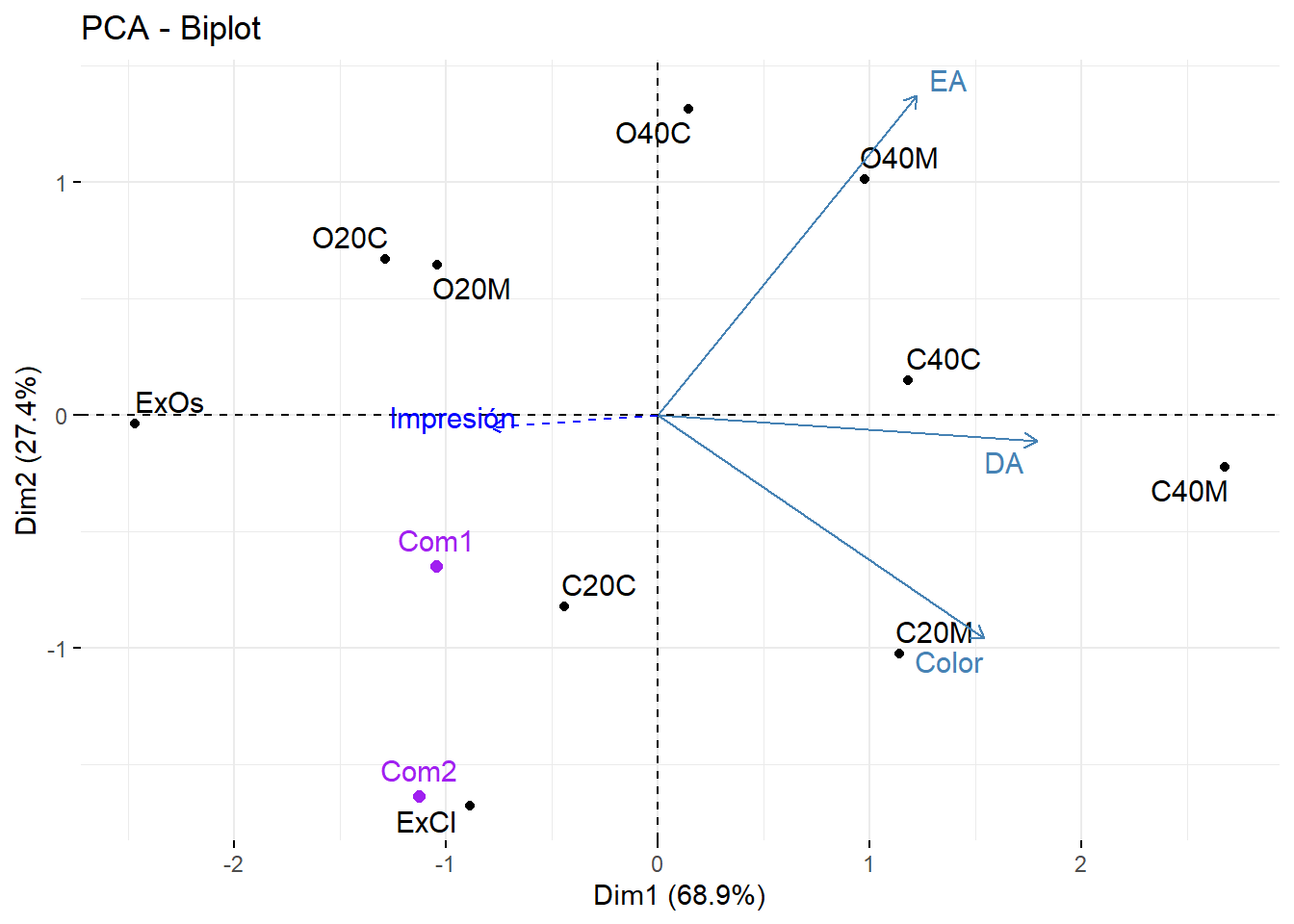

¿Cuál sería el resultado si hubiésemos usado más variables (por ejemplo, todas las físico-químicas)?

Código

library(Factoshiny) # cargar Factoshiny
res <- PCAshiny(cafe) # activar ACP para cafe

2.4 Ejemplo (ACP de examen de admisión)

Ejemplo de aplicación de ACP: resultados del examen de admisión a las carreras de la Facultad de Ciencias

data(admi)
summary(admi)

   carr         mate           cien            soci            text     
 Biol:63   Min.   : 9.3   Min.   : 9.37   Min.   : 9.02   Min.   : 8.2  
 Esta:66   1st Qu.:10.9   1st Qu.:10.84   1st Qu.:10.70   1st Qu.:10.9  
 Farm:73   Median :11.5   Median :11.48   Median :11.36   Median :11.2  
 Fisi:82   Mean   :11.8   Mean   :11.59   Mean   :11.36   Mean   :11.4  
 Geol:45   3rd Qu.:12.3   3rd Qu.:12.12   3rd Qu.:11.71   3rd Qu.:11.9  
 Mate:53   Max.   :18.3   Max.   :16.52   Max.   :14.84   Max.   :16.5  
 Quim:63                                                                
      imag            exam      gene       estr       orig       edad    
 Min.   : 8.48   Min.   : 477   F:128   bajo :179   Bogo:311   a16m:118  
 1st Qu.:10.68   1st Qu.: 667   M:317   medio:185   Cund: 38   a17 :171  
 Median :11.26   Median : 710           alto : 81   Otro: 96   a18 : 56  
 Mean   :11.30   Mean   : 718                                  a19M:100  
 3rd Qu.:12.01   3rd Qu.: 761                                            
 Max.   :14.71   Max.   :1151                                            
                                                                         
   niLE       niMa     stra          age      
 siLE: 46   siMa:315   E0:  2   Min.   :15.0  
 noLE:399   noMa:130   E1: 36   1st Qu.:16.0  
                       E2:141   Median :17.0  
                       E3:185   Mean   :18.1  
                       E4: 72   3rd Qu.:18.0  
                       E5:  8   Max.   :44.0  
                       E6:  1

Y <- admi[, 2:6]
plotpairs(Y)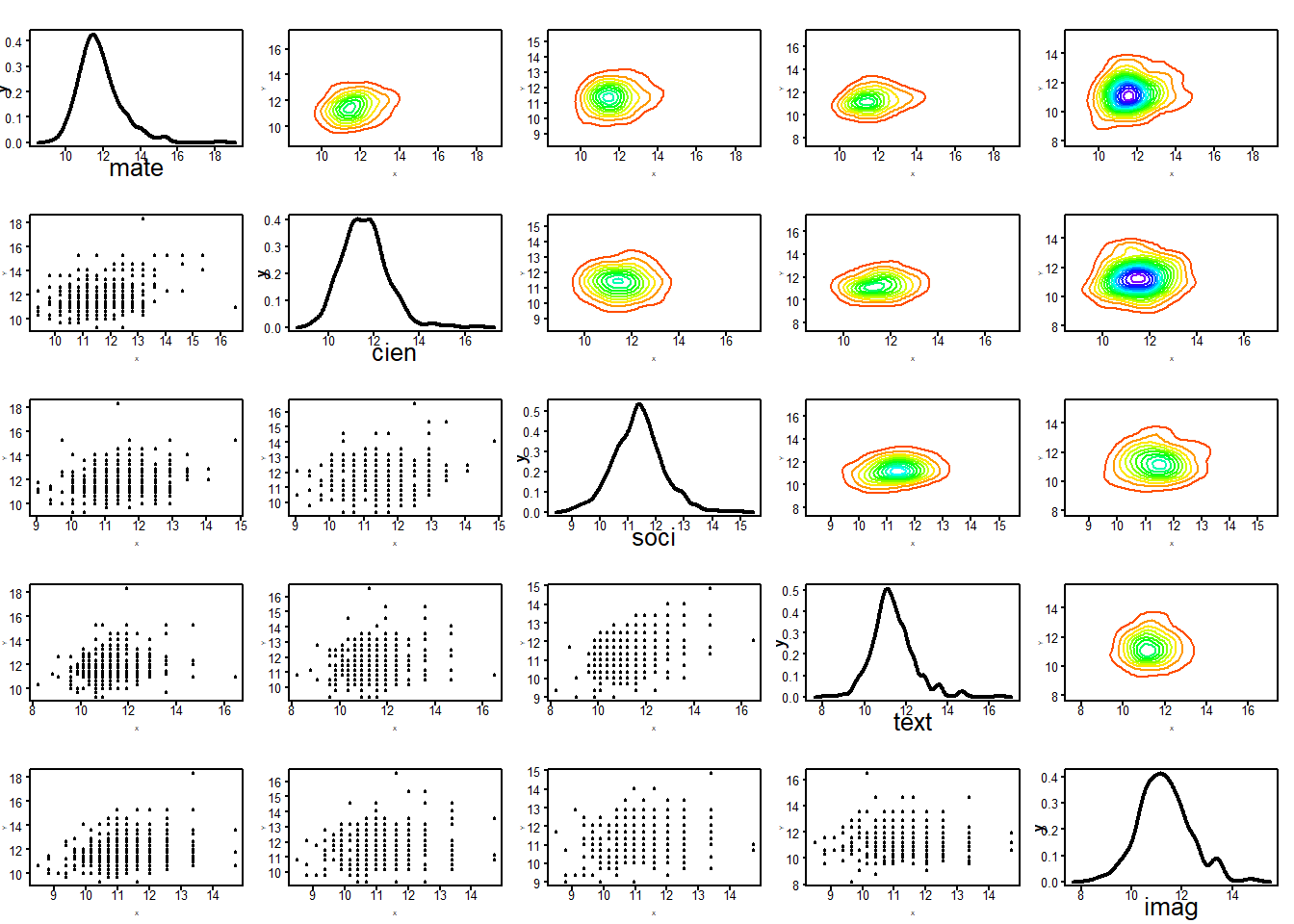

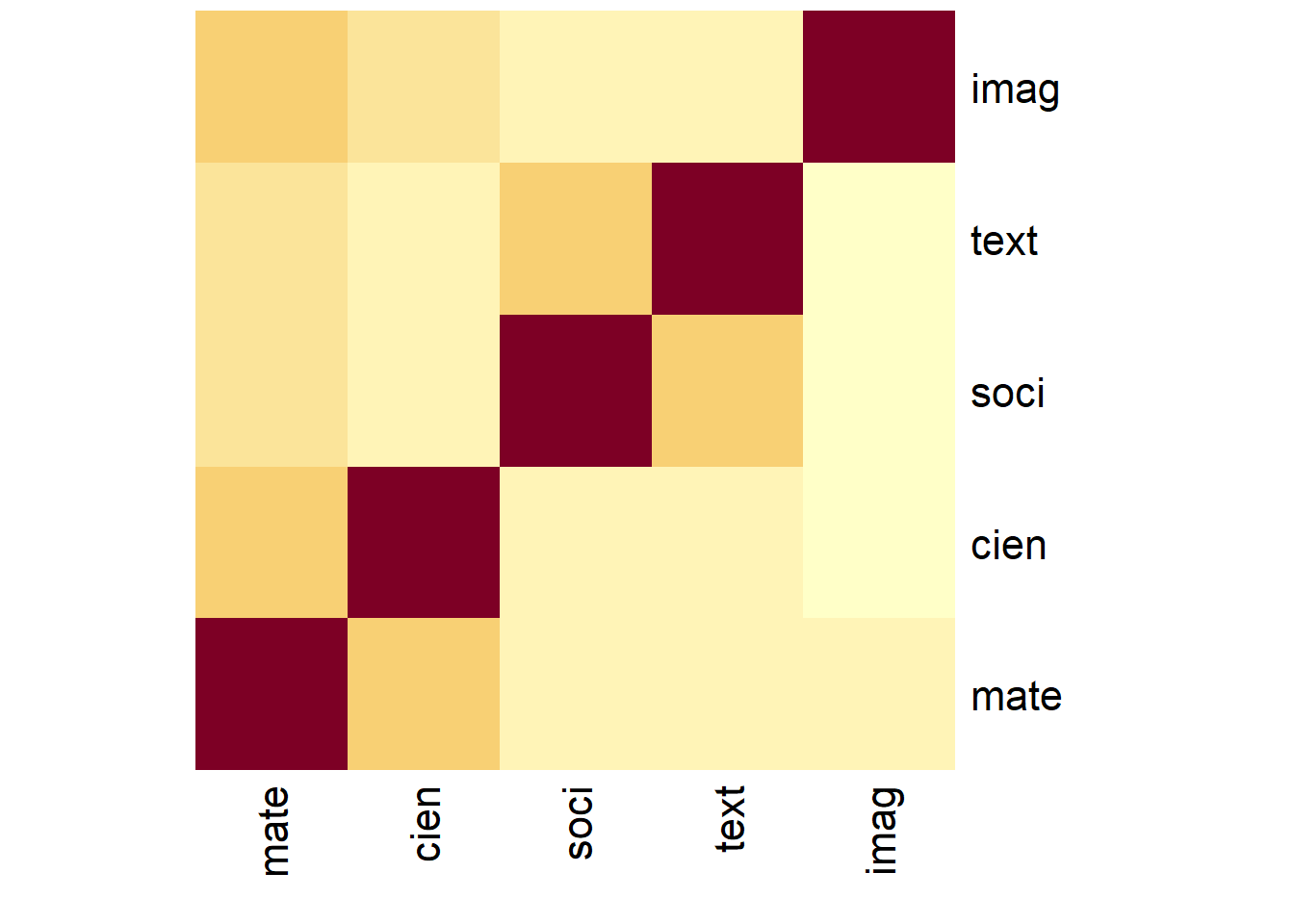
kable(cor(Y), digits = 3)

	mate	cien	soci	text	imag
mate	1.000	0.341	0.242	0.242	0.211
cien	0.341	1.000	0.160	0.202	0.123
soci	0.242	0.160	1.000	0.372	0.105
text	0.242	0.202	0.372	1.000	0.046
imag	0.211	0.123	0.105	0.046	1.000

heatmap(cor(Y), NA, NA)

ACP:

Código

# Con Factoshiny (y FactoMineR):
library(Factoshiny) # cargar Factoshiny
res <- PCAshiny(admi) # activar ACP para admi

# Con ade4 y FactoClass
acp <- dudi.pca(Y, scannf = FALSE, nf = 3)
valp <- t(inertia(acp)$tot.inertia) # valores propios
kable(valp, digits = 3)

	Ax1	Ax2	Ax3	Ax4	Ax5
inertia	1.852	1.025	0.870	0.638	0.616
cum	1.852	2.877	3.746	4.384	5.000
cum(%)	37.034	57.532	74.925	87.686	100.000

barplot(acp$eig, horiz = TRUE) # histograma de valores propios
abline(v = 1, lty = 3)

Código

# Con factoextra:
fviz_screeplot(acp, addlabels = TRUE, ylim = c(0, 50))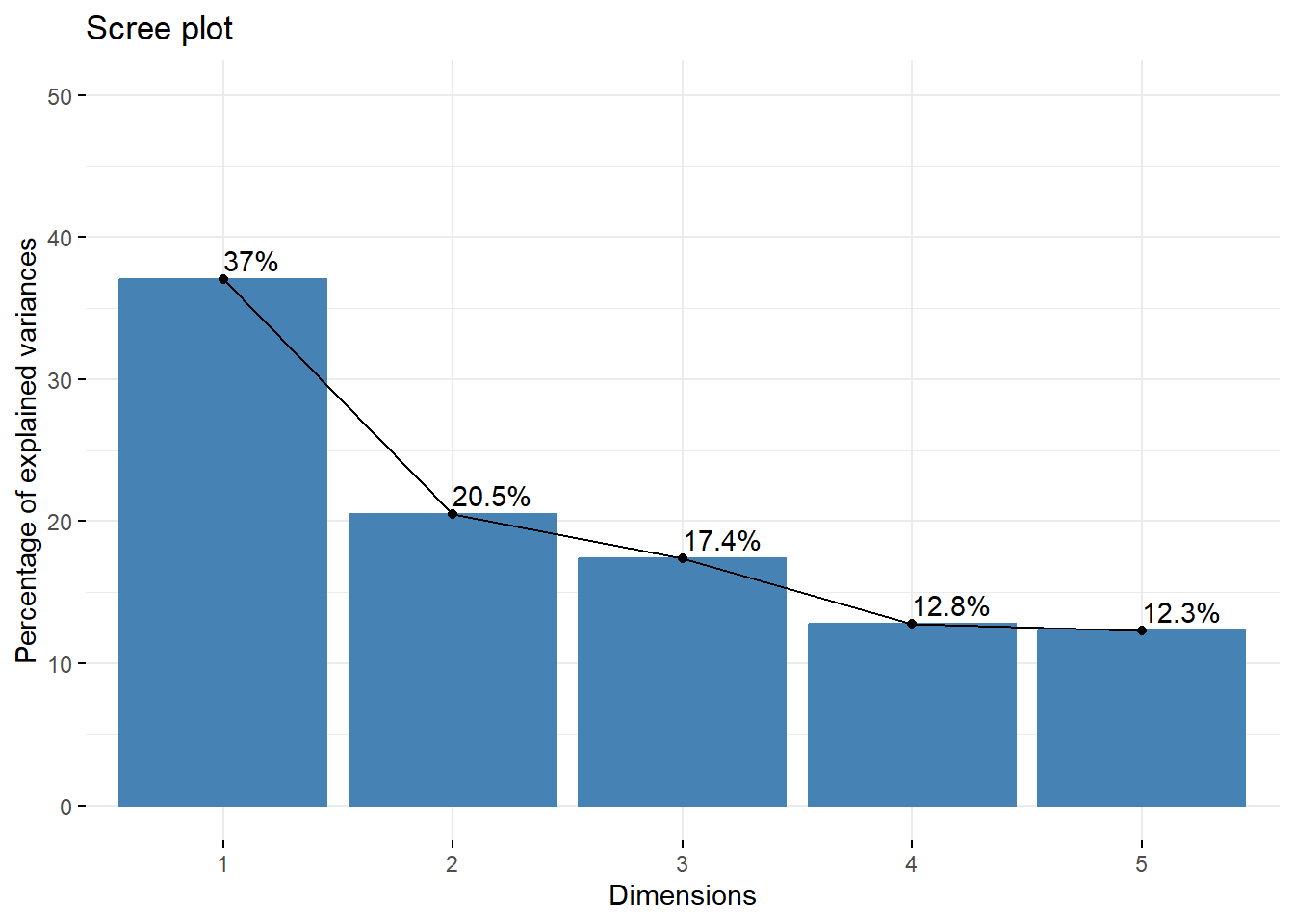

kable(acp$co, digits = 3)

	Comp1	Comp2	Comp3
mate	-0.706	0.259	0.204
cien	-0.612	0.242	0.602
soci	-0.645	-0.420	-0.351
text	-0.648	-0.496	-0.105
imag	-0.378	0.691	-0.576

# exam como ilustrativa
Gexam <- cor(admi$exam, acp$li)
rownames(Gexam)<-"exam"
kable(Gexam, digits = 3)

	Axis1	Axis2	Axis3
exam	-0.985	0.159	0.023

s.corcircle(acp$co)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE)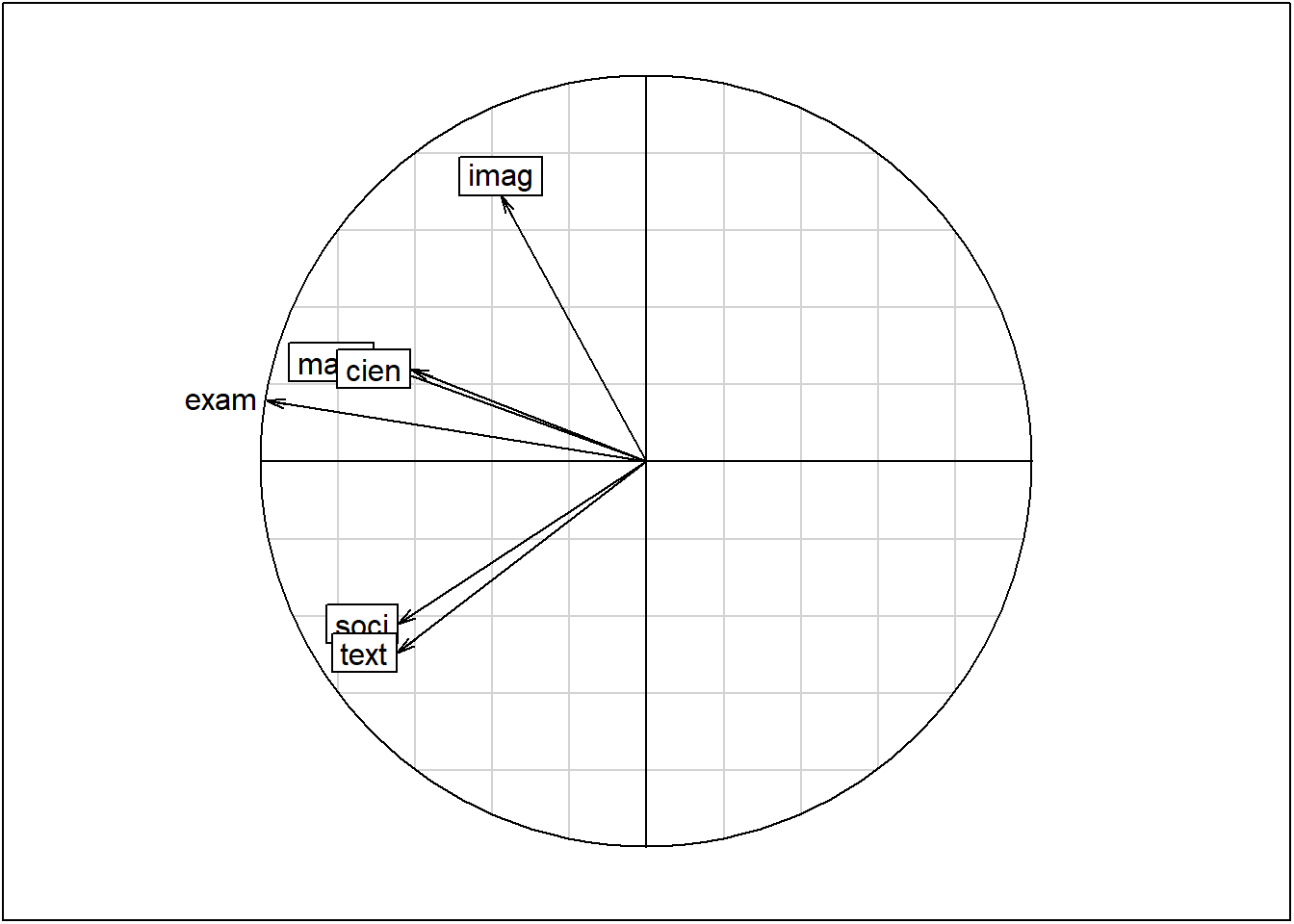

# Plano con los ejes 2 y 3
s.corcircle(acp$co, xax = 2, yax = 3)
s.arrow(Gexam, xax = 2, yax = 3, 
        add.plot = TRUE, boxes = FALSE)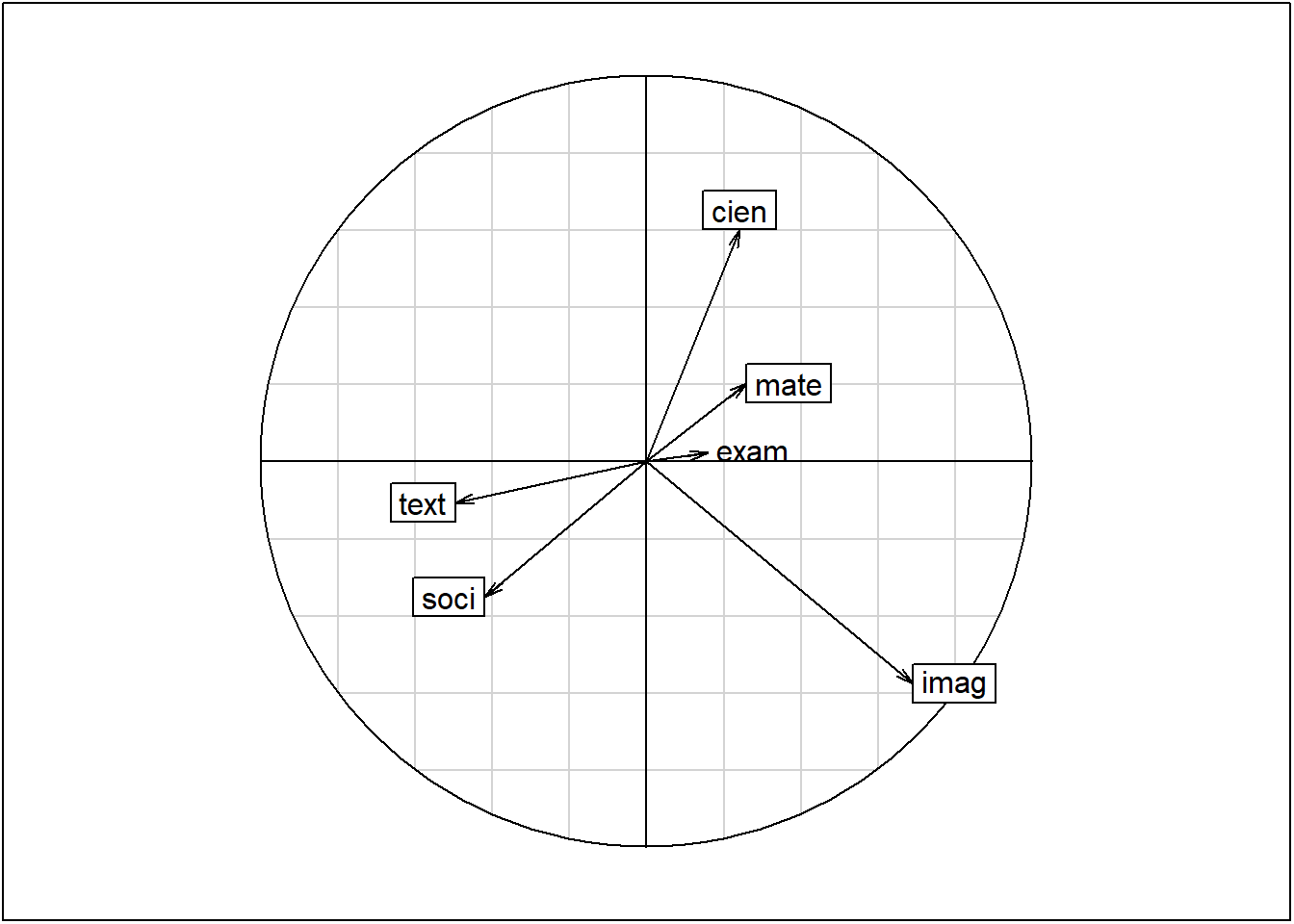

# Código experimental
G_df = as.data.frame(acp$co)
fig <- plot_ly(G_df, x = ~Comp1, y = ~Comp2, z = ~Comp3)
# Graficare como puntos pero sería mejor como flechas
fig <- fig %>% add_markers() 
fig <- fig %>% add_text(text = rownames(G_df))
fig <- fig %>% add_markers(x = 0, y = 0, z = 0)

sphere <- function(n = 100){
  theta <- seq(0, pi, length.out = n)
  phi <- seq(0, 2 * pi, length.out = n)
  r <- 1
  x <- r * outer(sin(theta), cos(phi))
  y <- r * outer(sin(theta), sin(phi))
  z <- r * outer(cos(theta), rep(1, length(phi)))
  return(list(x = x, y = y, z = z))
}
s_c <- sphere()
fig <- fig %>% add_trace(x = s_c$x, y = s_c$y, z = s_c$z, 
                         type = 'surface', opacity = 0.2, 
                         colorscale = "Greys", # cambiar por valor fijo
                         showscale = FALSE)

fig <- fig %>% layout(title = "vectores columna\n(variables)",
                      scene = list(xaxis = list(range = c(-1,1)),
                                   yaxis = list(range = c(-1,1)),
                                   zaxis = list(range = c(-1,1)),
                                   aspectratio = list(x=1,y=1,z=1),
                                   camera = list(eye = list(x=1,y=1,z=1))),
                      showlegend = FALSE)
fig

Ayudas numéricas para interpretación (y gráficos asociados):

Código

var <- get_pca_var(acp)
var

Principal Component Analysis Results for variables
 ===================================================
  Name       Description                                    
1 "$coord"   "Coordinates for the variables"                
2 "$cor"     "Correlations between variables and dimensions"
3 "$cos2"    "Cos2 for the variables"                       
4 "$contrib" "contributions of the variables"

Código

fviz_contrib(acp, choice = "var", axes = 3)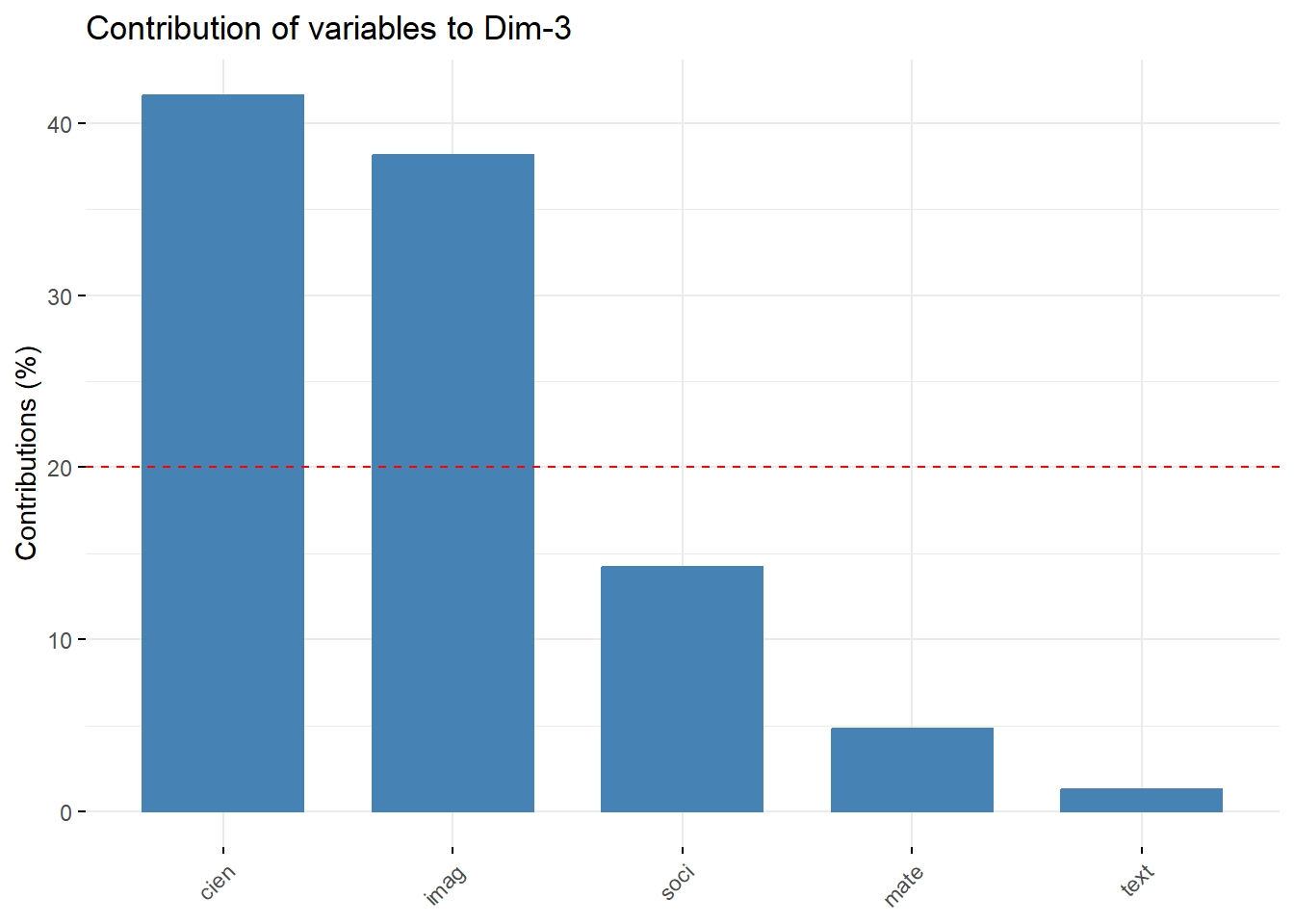

Código

fviz_pca_var(acp, axes=c(3,2), col.var="cos2",
             gradient.cols = c("darkred", 
                               "darkorange", 
                               "darkgreen"))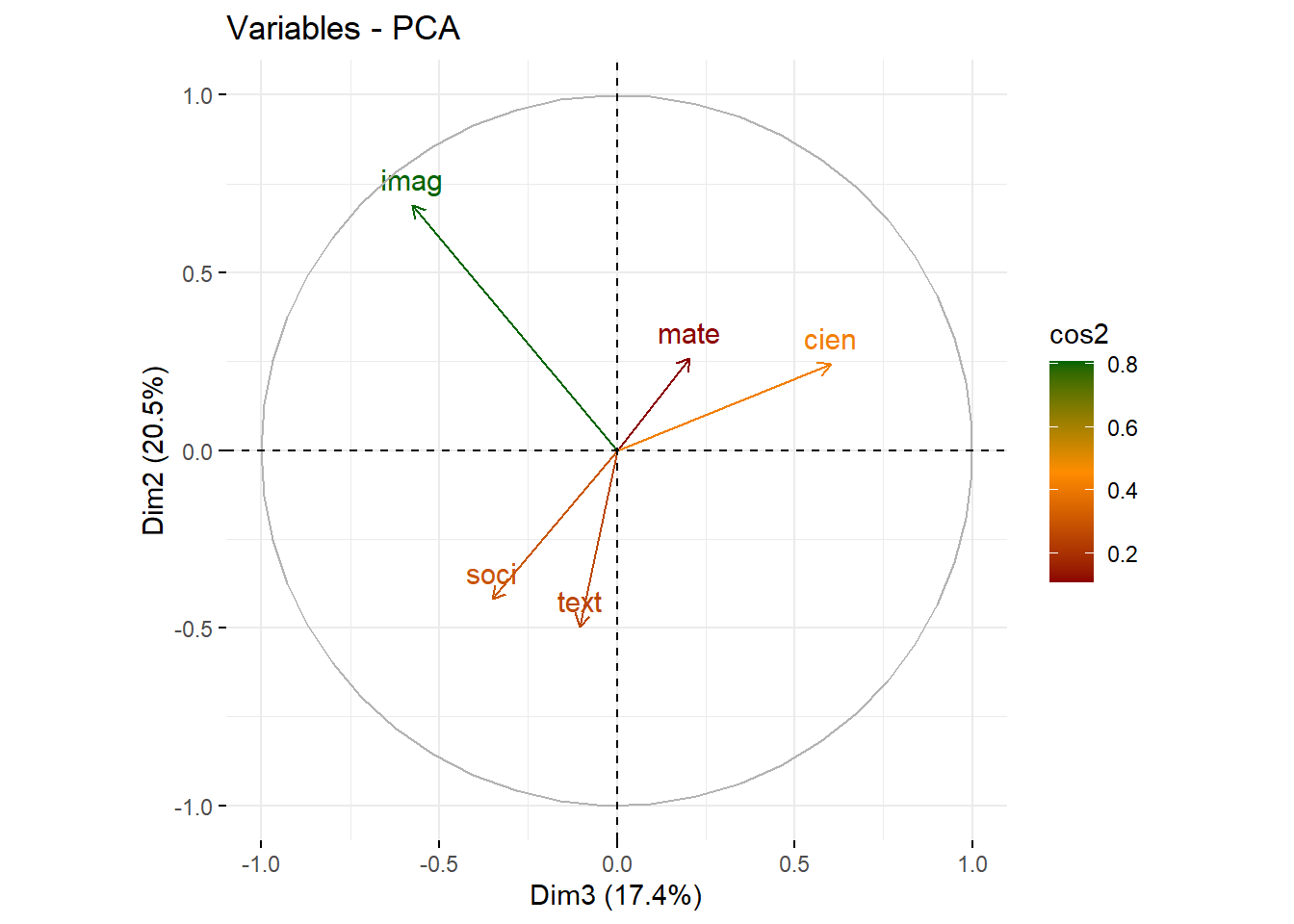

Elementos suplementarios:

Ysupcat <- admi[, c(1, 8:13)]
sup <- supqual(acp, Ysupcat)
kable(cbind(wcat = sup$wcat, d2 = sup$dis2, sup$coor), 
      digits = 3)

	wcat	d2	Axis1	Axis2	Axis3
Biol	0.142	0.117	-0.036	-0.152	-0.080
Esta	0.148	0.403	0.601	0.082	-0.109
Farm	0.164	0.346	0.427	-0.315	0.068
Fisi	0.184	0.214	-0.416	0.114	0.108
Geol	0.101	0.244	-0.483	-0.010	-0.071
Mate	0.119	0.751	-0.573	0.496	-0.014
Quim	0.142	0.106	0.280	-0.127	0.036
F	0.288	0.229	0.410	-0.211	0.117
M	0.712	0.037	-0.166	0.085	-0.047
bajo	0.402	0.267	0.506	0.088	0.035
medio	0.416	0.021	-0.099	-0.030	-0.068
alto	0.182	0.878	-0.891	-0.125	0.078
Bogo	0.699	0.040	-0.182	0.053	-0.062
Cund	0.085	0.080	0.039	-0.246	-0.025
Otro	0.216	0.382	0.573	-0.075	0.210
a16m	0.265	0.052	0.057	-0.079	0.195
a17	0.384	0.079	-0.220	0.044	-0.118
a18	0.126	0.162	0.372	-0.117	-0.068
a19M	0.225	0.059	0.102	0.084	0.011
siLE	0.103	3.636	1.698	0.654	0.388
noLE	0.897	0.048	-0.196	-0.075	-0.045
siMa	0.708	0.309	0.460	-0.116	-0.119
noMa	0.292	1.814	-1.115	0.281	0.287

kable(cbind(sup$tv, sup$cos2), digits = 3)

	Axis1	Axis2	Axis3	Axis1	Axis2	Axis3
Biol	-0.228	-1.287	-0.730	0.011	0.198	0.054
Esta	3.885	0.711	-1.024	0.897	0.017	0.029
Farm	2.928	-2.908	0.684	0.526	0.287	0.013
Fisi	-3.064	1.127	1.160	0.812	0.061	0.055
Geol	-2.507	-0.071	-0.540	0.956	0.000	0.021
Mate	-3.261	3.799	-0.114	0.437	0.328	0.000
Quim	1.763	-1.071	0.331	0.745	0.152	0.012
F	4.036	-2.793	1.675	0.733	0.194	0.059
M	-4.036	2.793	-1.675	0.733	0.194	0.059
bajo	6.430	1.496	0.642	0.961	0.029	0.005
medio	-1.300	-0.530	-1.292	0.468	0.043	0.217
alto	-6.512	-1.225	0.834	0.905	0.018	0.007
Bogo	-4.286	1.685	-2.129	0.828	0.071	0.096
Cund	0.186	-1.567	-0.174	0.019	0.755	0.008
Otro	4.654	-0.814	2.493	0.860	0.015	0.116
a16m	0.526	-0.989	2.649	0.062	0.121	0.738
a17	-2.697	0.717	-2.115	0.616	0.024	0.178
a18	2.188	-0.921	-0.585	0.855	0.084	0.029
a19M	0.847	0.942	0.128	0.176	0.120	0.002
siLE	8.927	4.624	2.973	0.793	0.118	0.041
noLE	-8.927	-4.624	-2.973	0.793	0.118	0.041
siMa	11.093	-3.763	-4.171	0.685	0.044	0.046
noMa	-11.093	3.763	4.171	0.685	0.044	0.046

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2,
     xlim = c(-1,1.5), ylim = c(-0.6,0.6))
points(sup$coor, col = 2, pch = 16)
text(sup$coor, labels = rownames(sup$coor),
     col = 2, pos = 1, font = 3)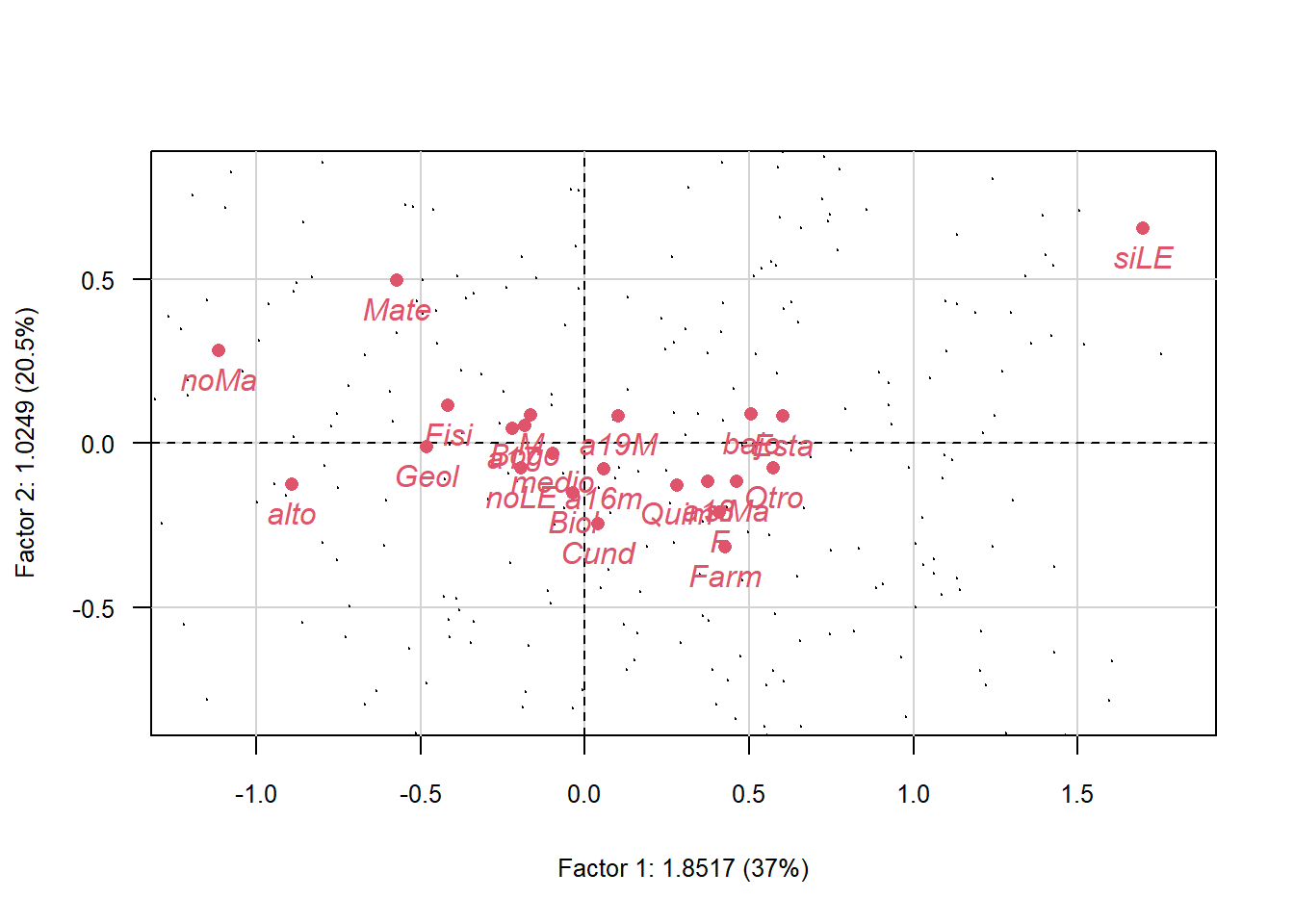

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2,
     xlim = c(-1,1.5), ylim = c(-0.6,0.6))
s.arrow(acp$co, add.plot = TRUE, boxes = FALSE)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE)
points(sup$coor[8:9,], col = 3, pch = 16)
text(sup$coor[8:9,], labels = rownames(sup$coor[8:9,]),
     col = 3, pos = 1, font = 3)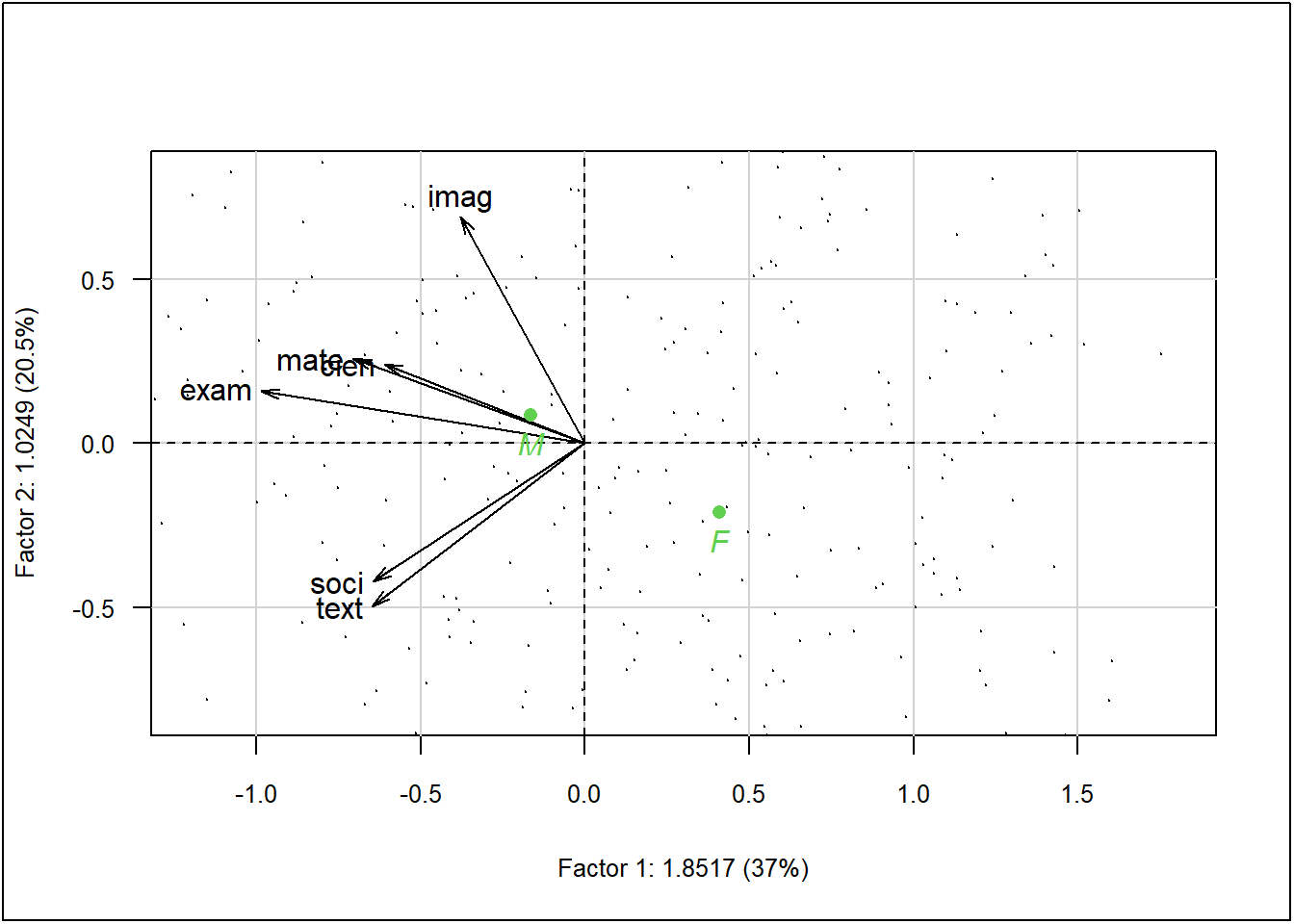

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2,
     xlim = c(-1,1.5), ylim = c(-0.6,0.6))
s.arrow(acp$co, add.plot = TRUE, boxes = FALSE)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE)
points(sup$coor[16:19,], col = 5, pch = 16)
text(sup$coor[16:19,], labels = rownames(sup$coor[16:19,]),
     col = 5, pos = 1, font = 3)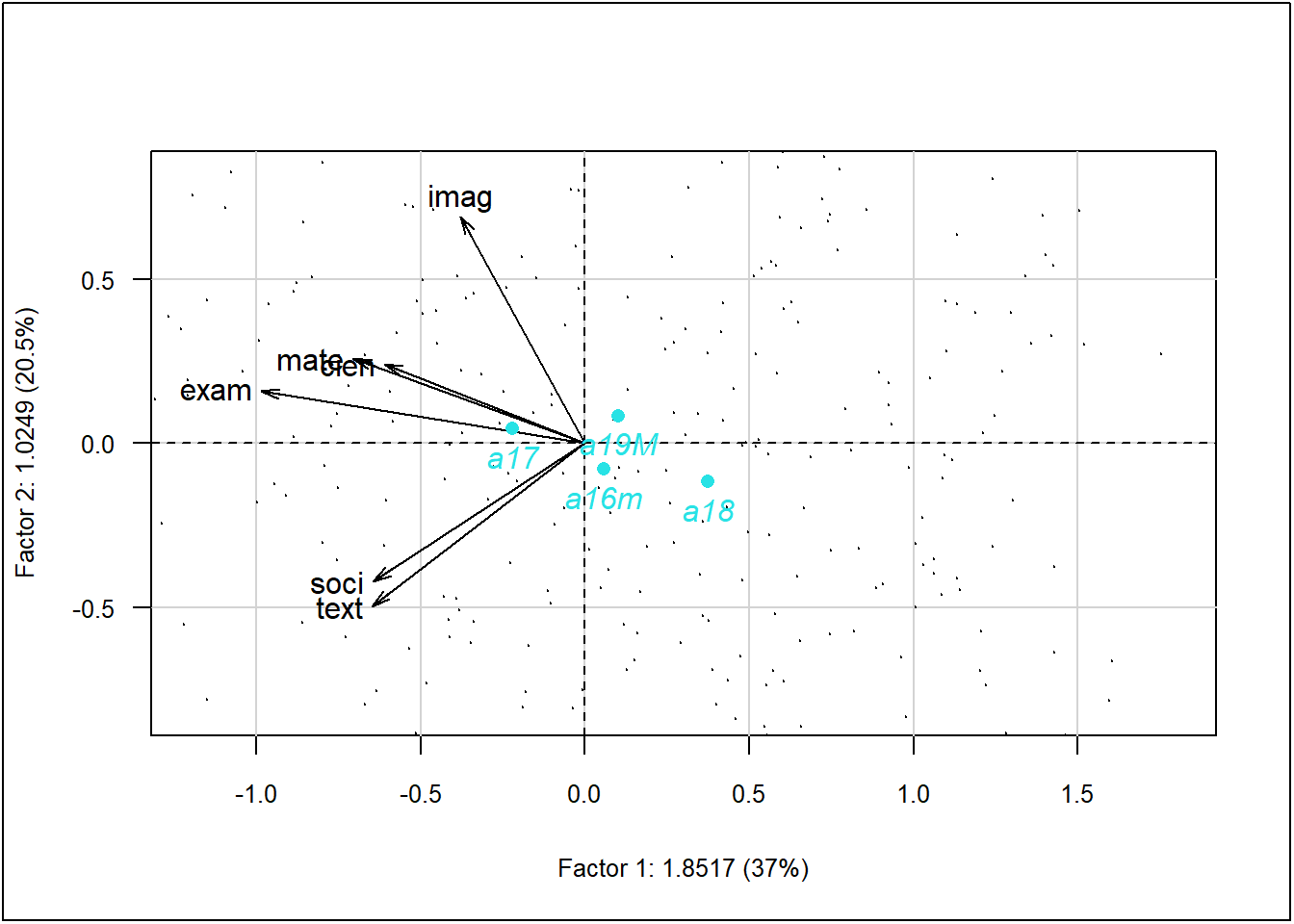

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2,
     xlim = c(-1,1.5), ylim = c(-0.6,0.6))
s.arrow(acp$co, add.plot = TRUE, boxes = FALSE)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE)
points(sup$coor[1:7,], col = 6, pch = 16)
text(sup$coor[1:7,], labels = rownames(sup$coor[1:7,]),
     col = 6, pos = 1, font = 3)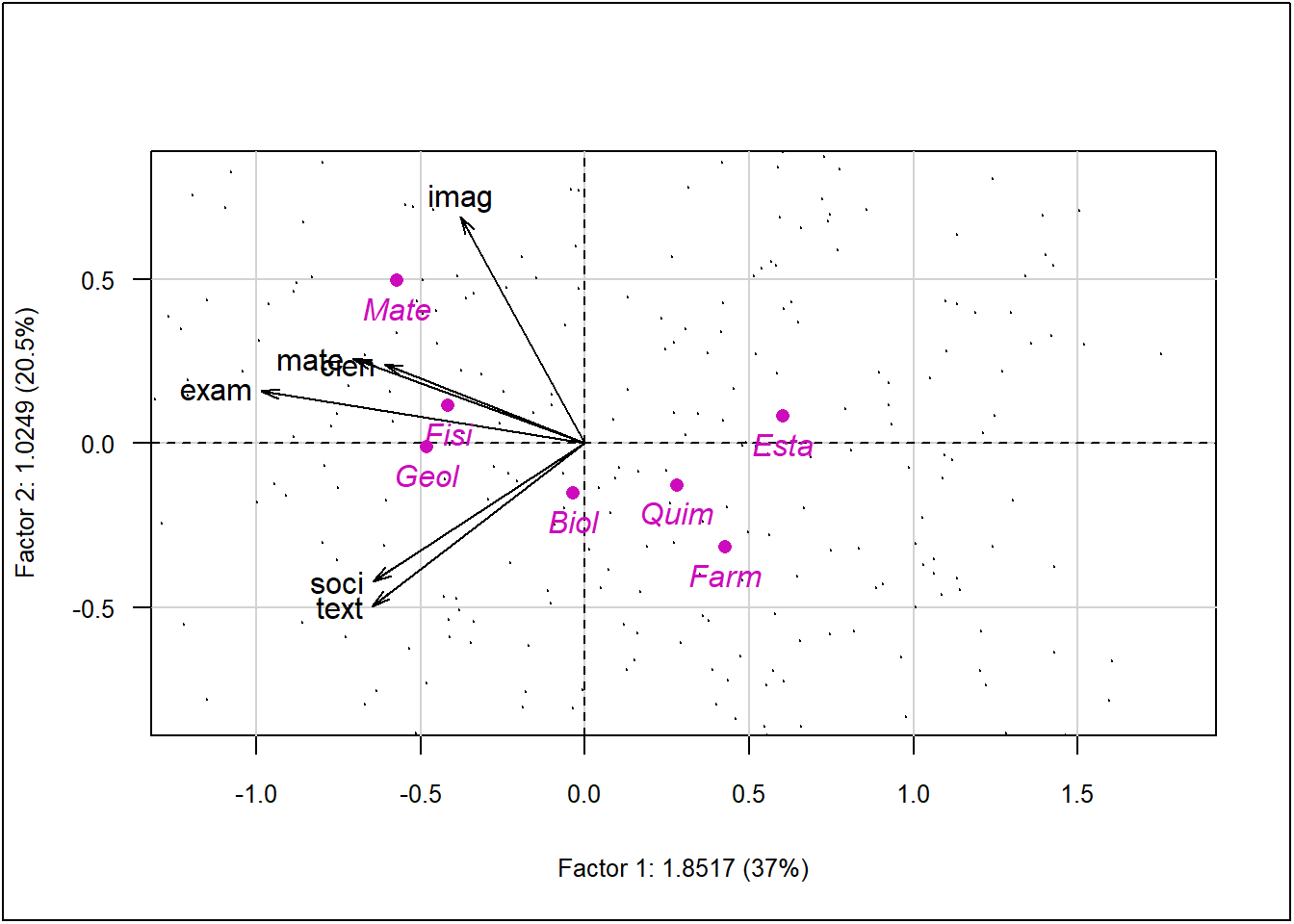

plot(sup$coor[1:7,2:3], col = 6, pch = 16,
     xlim = c(-1,1), ylim = c(-1,1),
     bty="n", axes = FALSE)
text(sup$coor[1:7,2:3], labels = rownames(sup$coor[1:7,]),
     col = 6, pos = 1, font = 3)
curve(sqrt(1 - x*x), -1, 1, 1e4, add = TRUE, lty = 3)
curve(-sqrt(1 - x*x), -1, 1, 1e4, add = TRUE, lty = 3)
abline(h=0, col="grey"); abline(v=0, col="grey")
s.arrow(acp$co, add.plot = TRUE, boxes = FALSE,
        xax = 2, yax = 3)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE,
        xax = 2, yax = 3)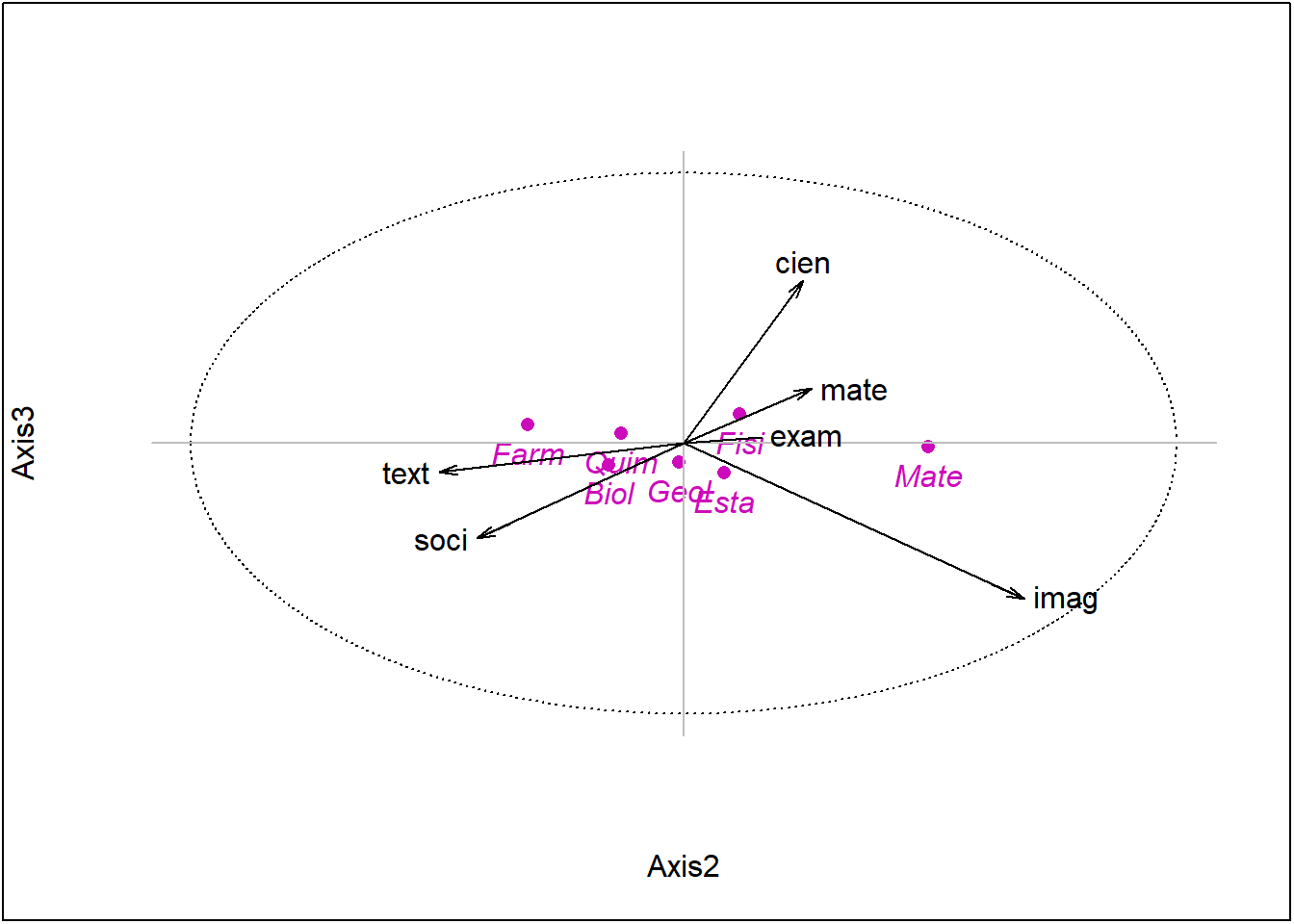

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2)
ade4::s.class(acp$li, admi[, 1], col = rainbow(8)[2:8], 
              add.plot = TRUE, clabel = 0.5)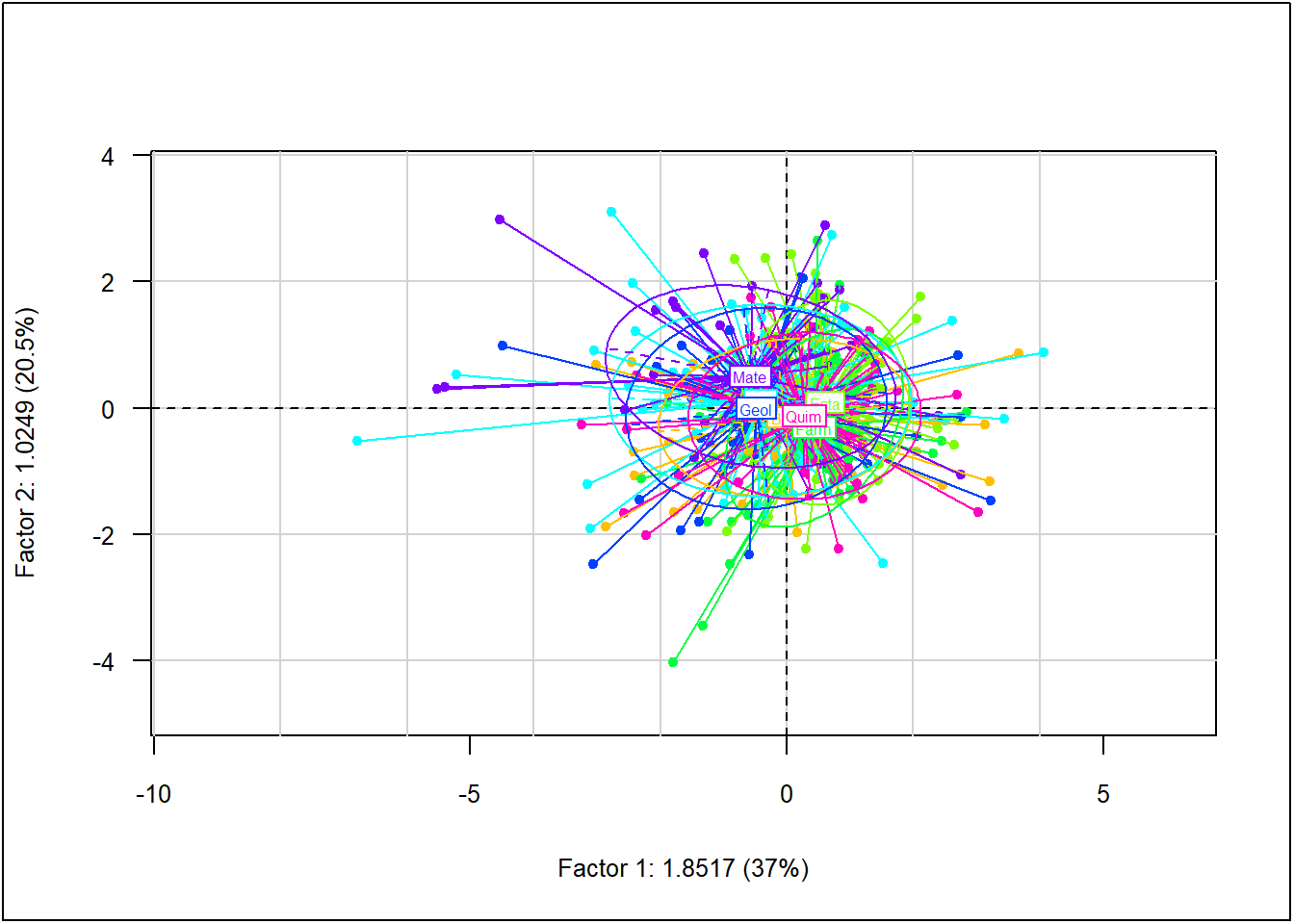

plot(acp, Tcol = FALSE, ucal = 100, cex.row = 0.2,
     xlim = c(-1,1.5), ylim = c(-0.6,0.6))
s.arrow(acp$co, add.plot = TRUE, boxes = FALSE)
s.arrow(Gexam, add.plot = TRUE, boxes = FALSE)
points(sup$coor[10:12,], col = 4, pch = 16)
text(sup$coor[10:12,], labels = rownames(sup$coor[10:12,]),
     col = 4, pos = 1, font = 3)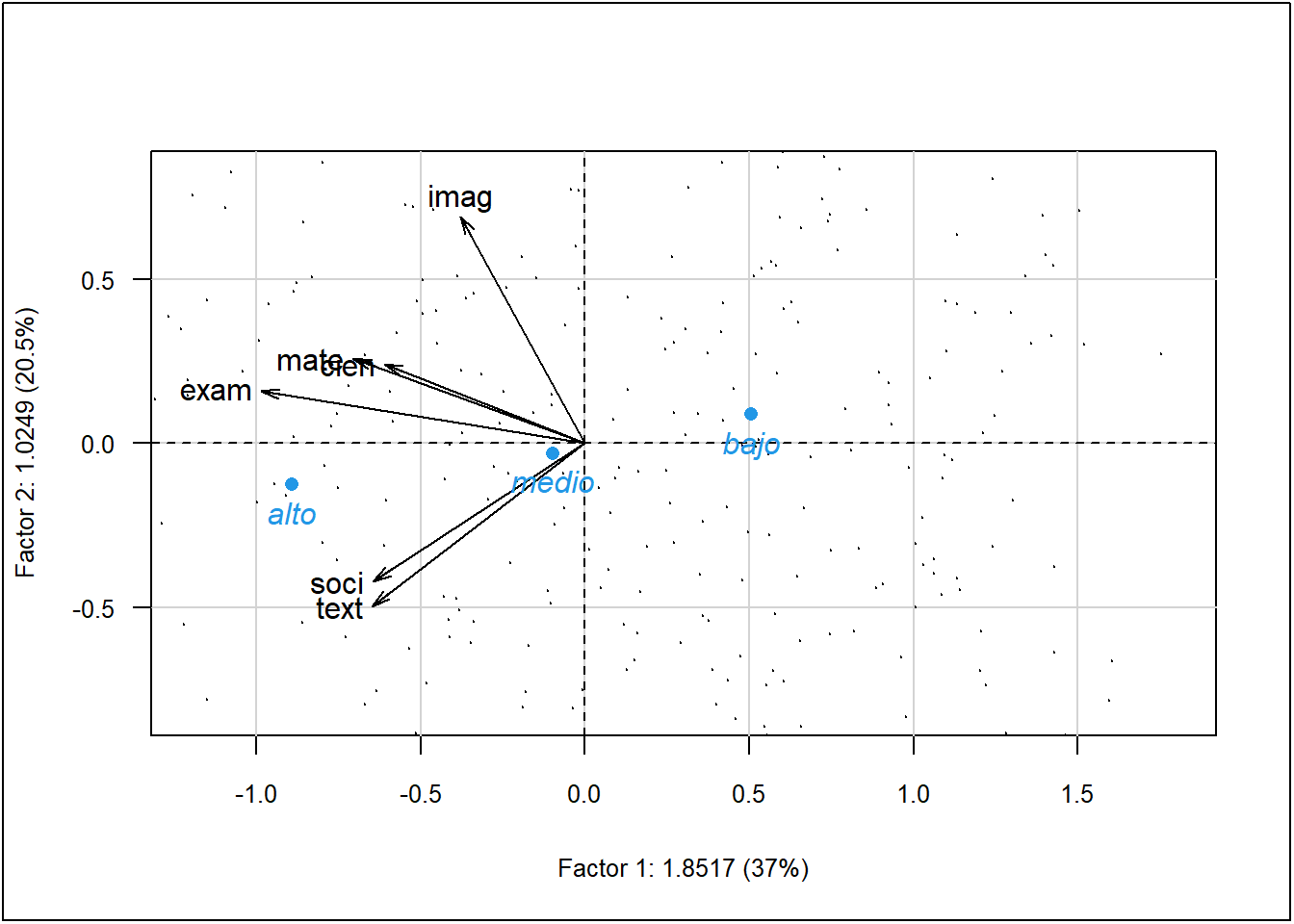

fviz_pca_biplot(acp, label = "var",
                habillage = admi$estr,
                addEllipses = TRUE)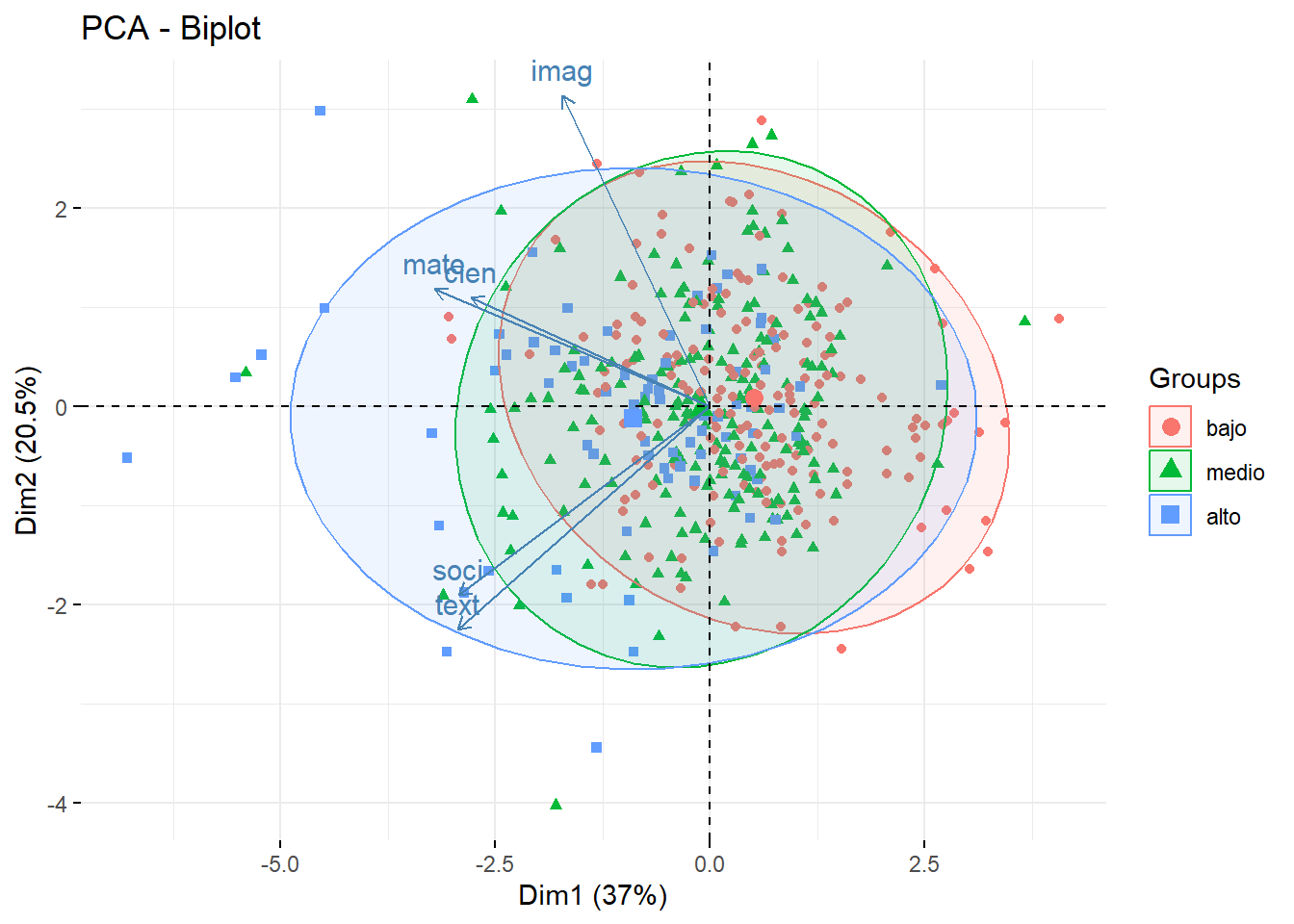

fviz_pca_biplot(acp, axes = c(3,2), 
                label = "var",
                habillage = admi$estr,
                addEllipses = TRUE)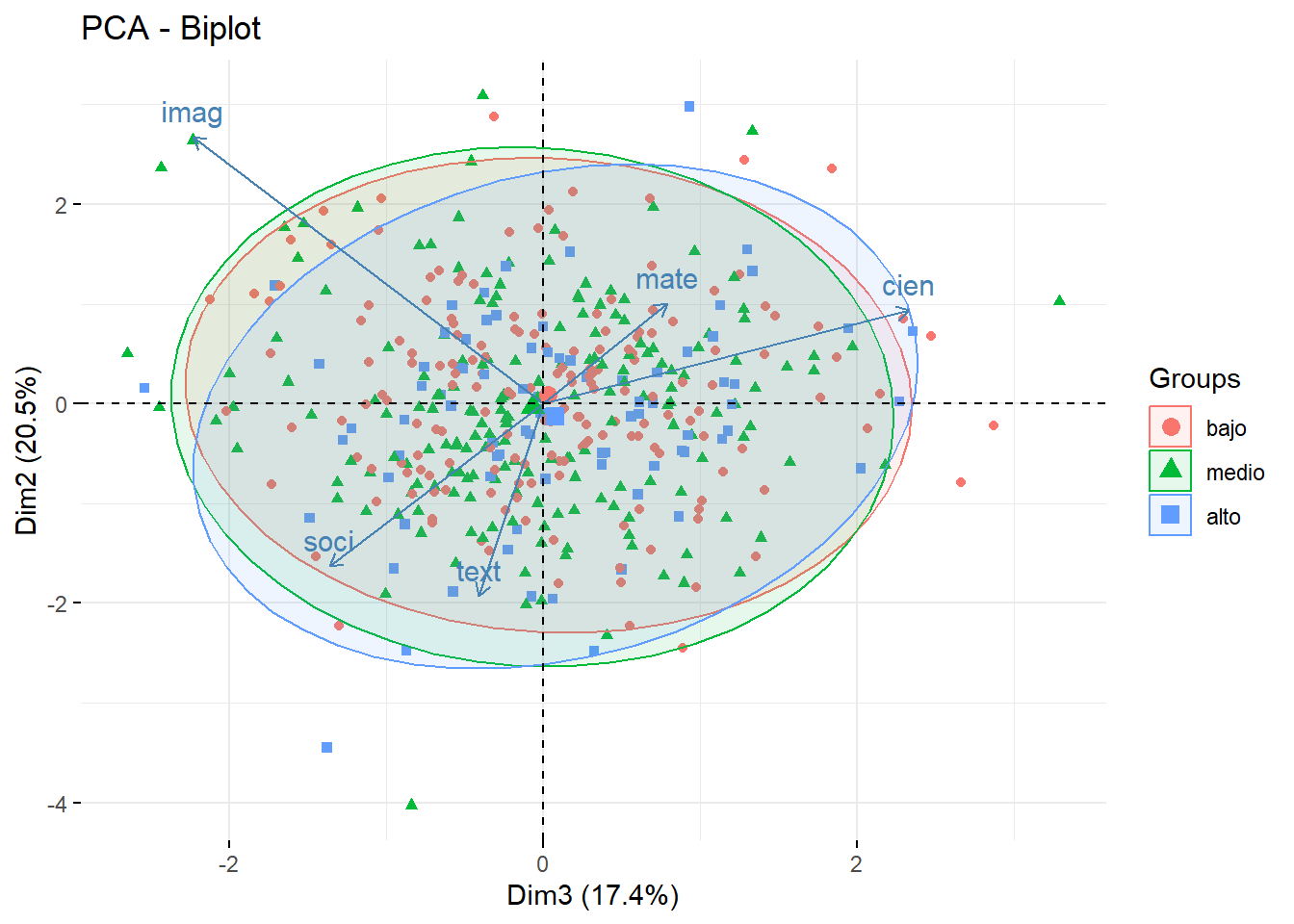

2.5 Taller (ACP de whisky)

data(Whisky)
data <- Whisky[, c(1,2,4,5)] 
summary(data)

     price            malt           aging           taste     
 Min.   : 55.0   Min.   : 20.0   Min.   : 5.00   Min.   :0.00  
 1st Qu.: 73.0   1st Qu.: 30.0   1st Qu.: 8.00   1st Qu.:2.00  
 Median : 83.0   Median : 40.0   Median :10.00   Median :2.00  
 Mean   : 85.7   Mean   : 47.4   Mean   : 9.53   Mean   :2.23  
 3rd Qu.: 91.5   3rd Qu.: 45.0   3rd Qu.:12.00   3rd Qu.:3.00  
 Max.   :160.0   Max.   :100.0   Max.   :12.50   Max.   :4.00

summary(Whisky[, 3])

 low  med pure 
  11   17    7

cov(data) # Muestral

        price    malt   aging  taste
price 395.563 359.735 24.8908 7.6261
malt  359.735 758.247 27.6941 8.7882
aging  24.891  27.694  6.7197 0.9345
taste   7.626   8.788  0.9345 1.4756

Yc <- scale(data, scale = FALSE)
n <- nrow(Yc)
Cov <- (t(Yc) %*% Yc) / n  # Poblacional
# aproximadamente igual a: cov(data) * (n-1) / n

cor(data)

       price   malt  aging  taste
price 1.0000 0.6569 0.4828 0.3156
malt  0.6569 1.0000 0.3880 0.2627
aging 0.4828 0.3880 1.0000 0.2968
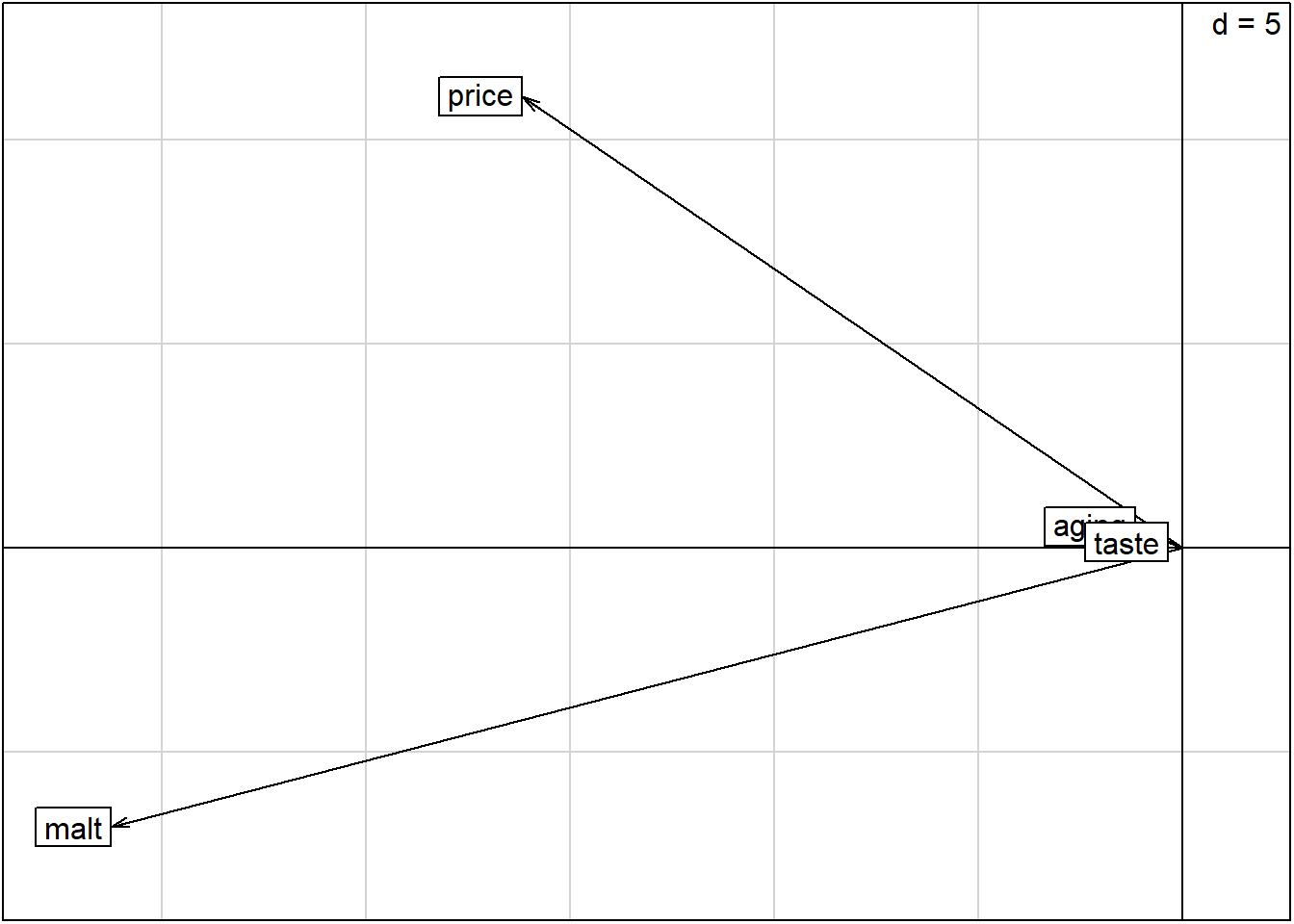
taste 0.3156 0.2627 0.2968 1.0000

acp <- dudi.pca(data, scannf = FALSE, nf = n, scale = FALSE)
s.arrow(acp$co)

acp <- dudi.pca(data, scannf = FALSE, nf = n)
s.corcircle(acp$co)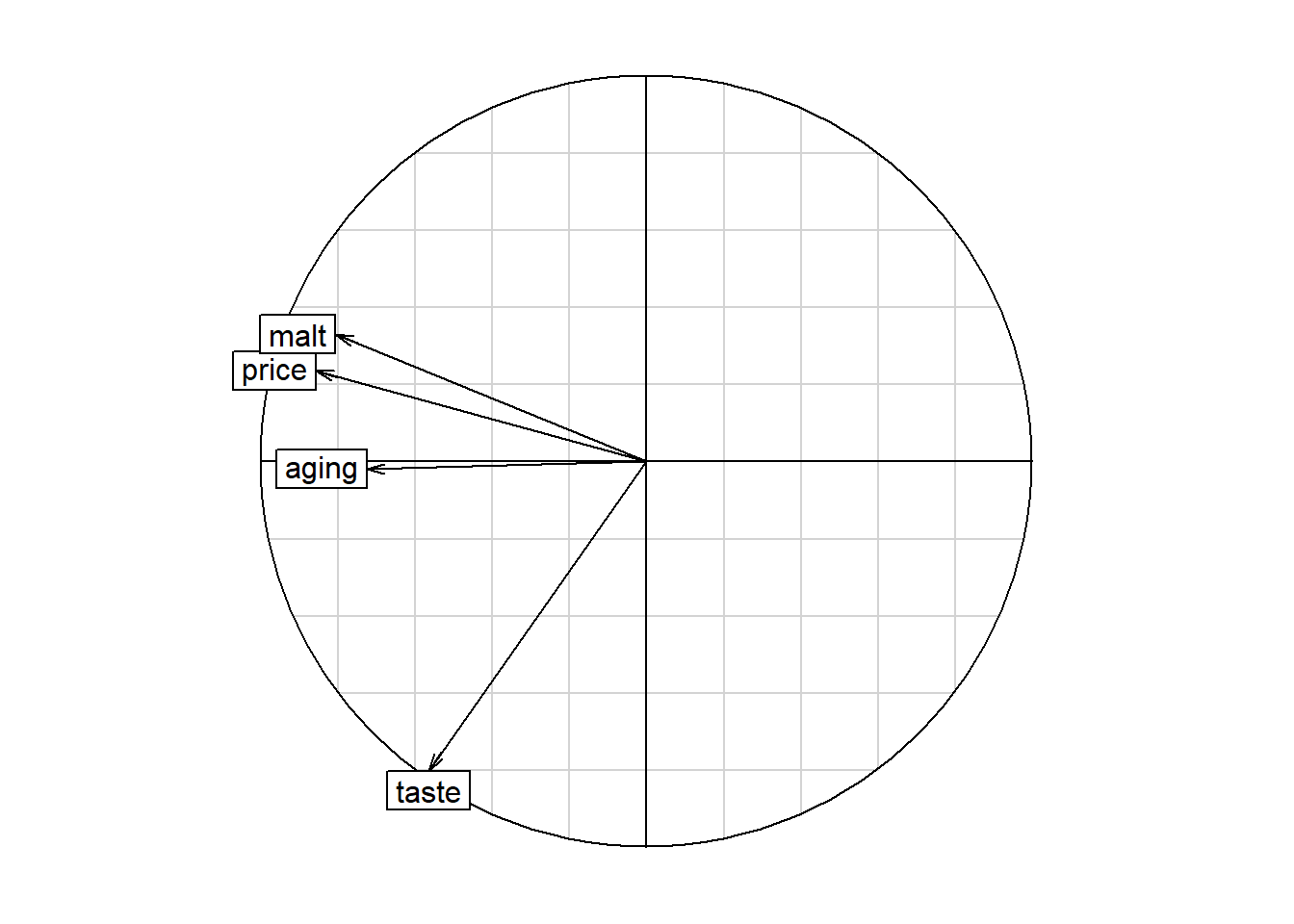

inertia_acp <- inertia(acp, row.inertia = TRUE, col.inertia = TRUE)
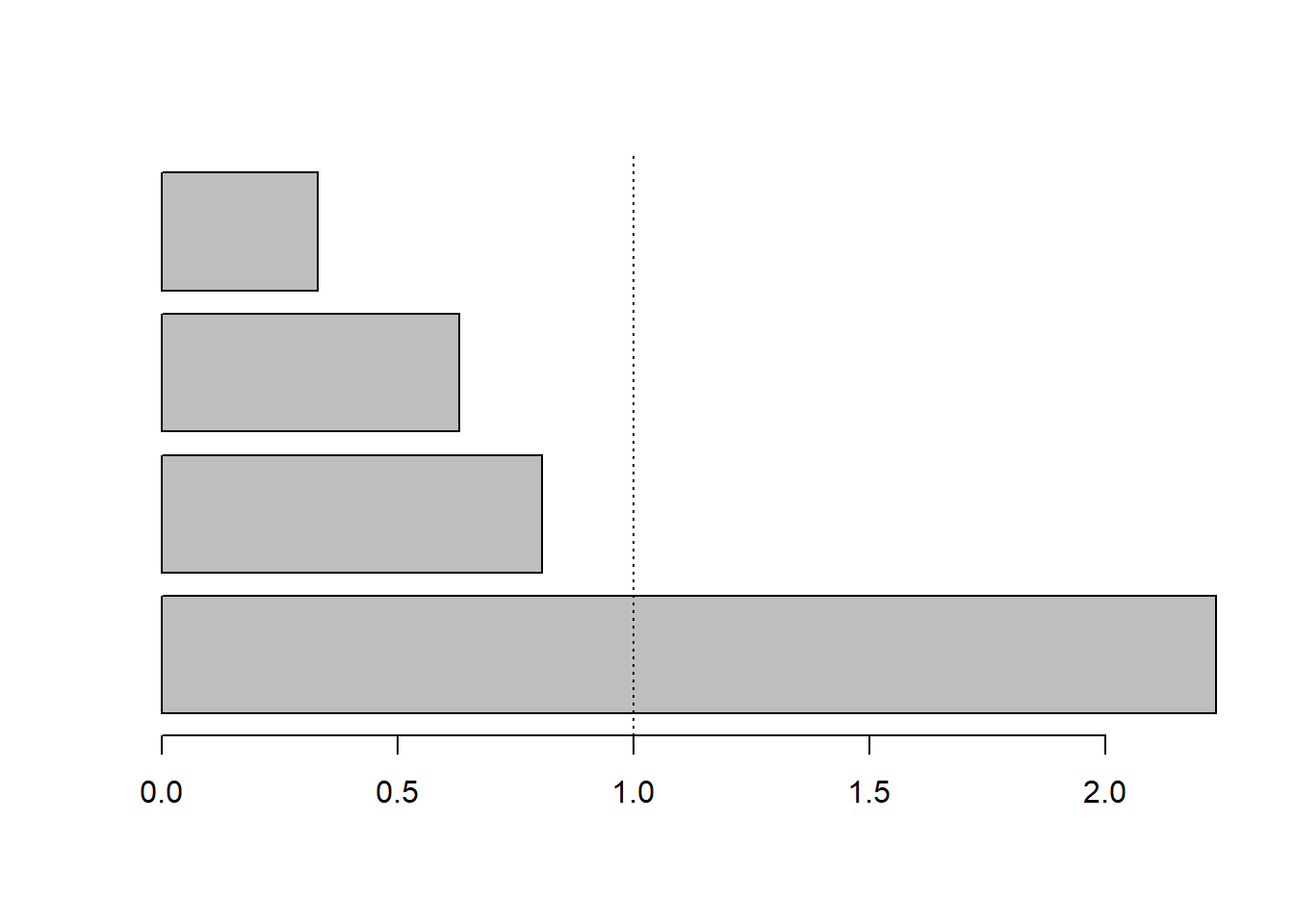
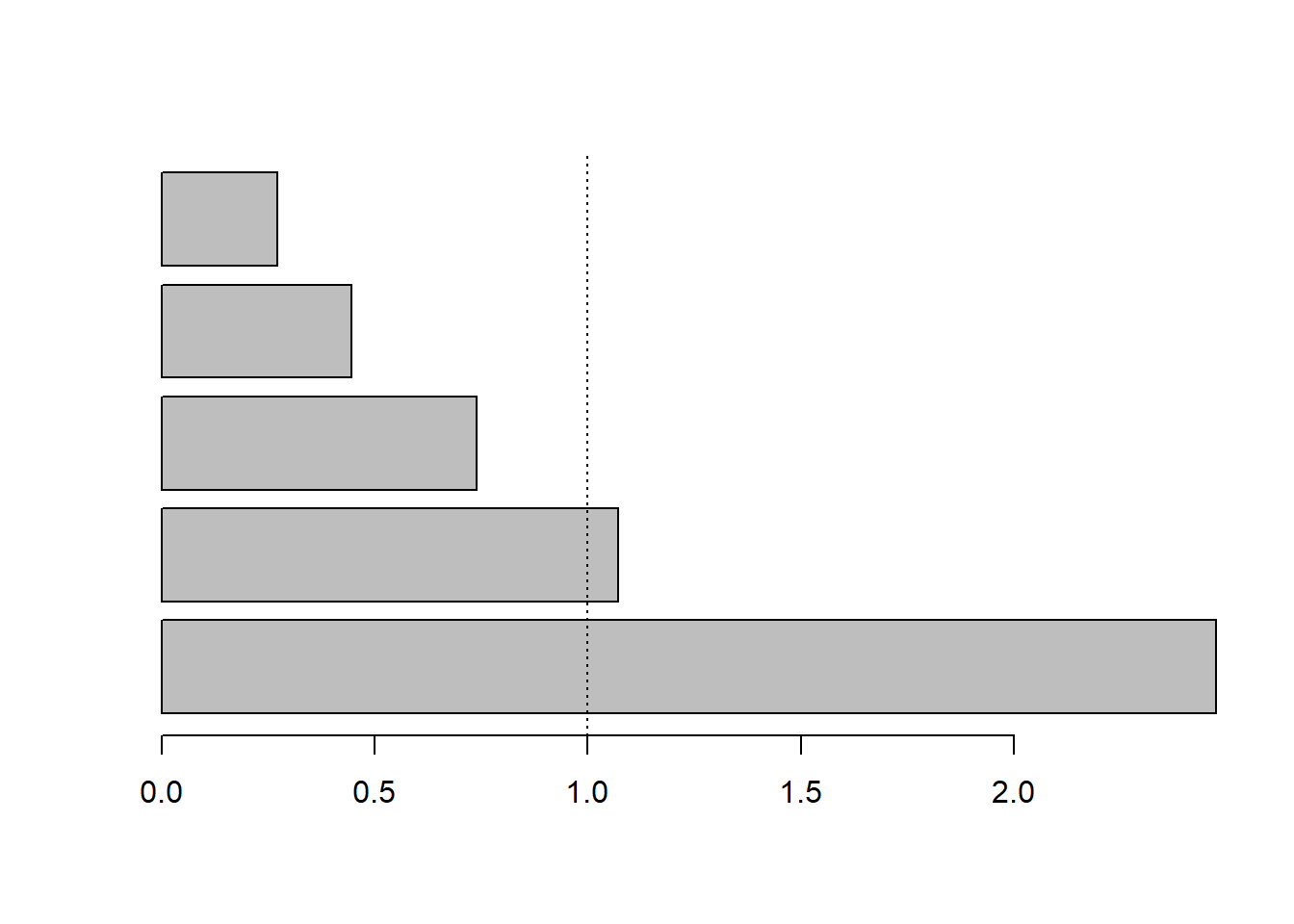
valp <- t(inertia_acp$tot.inertia) # valores propios
kable(valp, digits = 2)

	Ax1	Ax2	Ax3	Ax4
inertia	2.23	0.81	0.63	0.33
cum	2.23	3.04	3.67	4.00
cum(%)	55.83	75.99	91.73	100.00

barplot(acp$eig, horiz = TRUE) # histograma de valores propios
abline(v = 1, lty = 3)

kable(inertia_acp$col.abs, digits = 1)

	Axis1	Axis2	Axis3	Axis4
price	33.0	6.8	3.1	57.1
malt	29.1	13.5	17.2	40.2
aging	23.6	0.0	73.7	2.6
taste	14.3	79.6	6.0	0.1

kable(inertia_acp$col.rel, digits = 1)

	Axis1	Axis2	Axis3	Axis4
price	-73.7	5.5	1.9	18.9
malt	-65.0	10.9	10.8	-13.3
aging	-52.7	0.0	-46.4	-0.9
taste	-32.0	-64.2	3.7	0.0

kable(inertia_acp$row.abs, digits = 1)

Axis1	Axis2	Axis3	Axis4
3.4	4.4	5.7	0.8
6.4	0.9	3.1	0.0
3.3	0.7	0.0	0.0
0.2	0.3	8.0	0.1
0.0	4.4	6.1	0.6
6.7	5.9	2.1	0.6
4.2	5.3	0.5	0.0
6.1	0.7	4.0	2.0
5.5	6.4	1.4	1.3
0.2	8.0	10.0	3.1
0.0	0.1	6.3	0.1
3.4	1.2	0.9	0.0
1.4	4.1	0.3	2.2
0.3	2.1	3.5	0.4
0.3	0.0	1.0	0.0
0.1	9.0	0.2	1.6
0.2	0.0	0.2	0.7
0.4	0.0	0.1	0.0
0.1	0.0	0.1	0.2
0.1	6.9	1.7	0.5
0.2	0.0	0.2	0.0
0.5	2.2	0.6	0.1
0.3	0.0	5.7	0.2
2.1	0.5	1.5	7.5
1.1	0.1	6.6	2.0
4.1	3.6	0.3	7.0
1.2	0.9	1.7	0.6
0.4	1.6	2.5	0.6
8.8	0.0	16.1	1.2
19.8	4.3	2.9	18.3
6.2	1.2	0.6	14.0
2.7	2.7	0.0	16.1
4.1	0.4	3.9	4.6
5.1	0.4	1.6	5.4
1.5	21.7	0.7	8.0

kable(inertia_acp$row.rel, digits = 1)

Axis1	Axis2	Axis3	Axis4
50.4	-23.9	24.0	1.7
84.1	-4.3	11.5	-0.1
92.4	-7.5	0.0	0.0
7.6	-4.8	-87.3	-0.3
1.4	-46.0	-50.0	-2.6
70.1	22.5	6.4	1.0
66.6	30.9	-2.5	0.0
78.5	-3.1	14.4	-3.9
65.4	27.5	4.7	2.3
2.7	45.5	-44.6	7.2
0.2	-1.3	-97.5	0.9
83.3	10.5	5.9	0.2
41.9	-45.7	2.3	-10.1
-13.2	-36.6	-47.5	2.6
47.7	-2.5	-49.5	-0.2
-1.8	-90.3	-1.3	-6.6
51.3	3.3	14.1	31.3
94.8	0.0	5.1	0.2
53.8	3.3	-21.8	21.1
-2.7	-80.0	15.1	2.3
78.5	0.0	-20.7	-0.8
33.6	52.9	-12.5	1.0
-14.7	0.7	-83.0	1.6
-55.2	-4.7	-10.9	29.2
34.5	0.6	55.9	9.0
-62.6	-20.1	-1.4	15.9
-57.3	-14.8	-23.4	4.6
-22.3	-33.0	-39.6	-5.1
-65.1	0.0	33.5	1.3
-79.6	6.3	3.3	10.9
-69.9	-4.7	2.0	-23.4
-44.5	15.9	-0.1	-39.5
-68.2	2.2	18.3	-11.3
-78.5	2.0	7.0	-12.5
-14.0	73.1	-1.9	-11.0

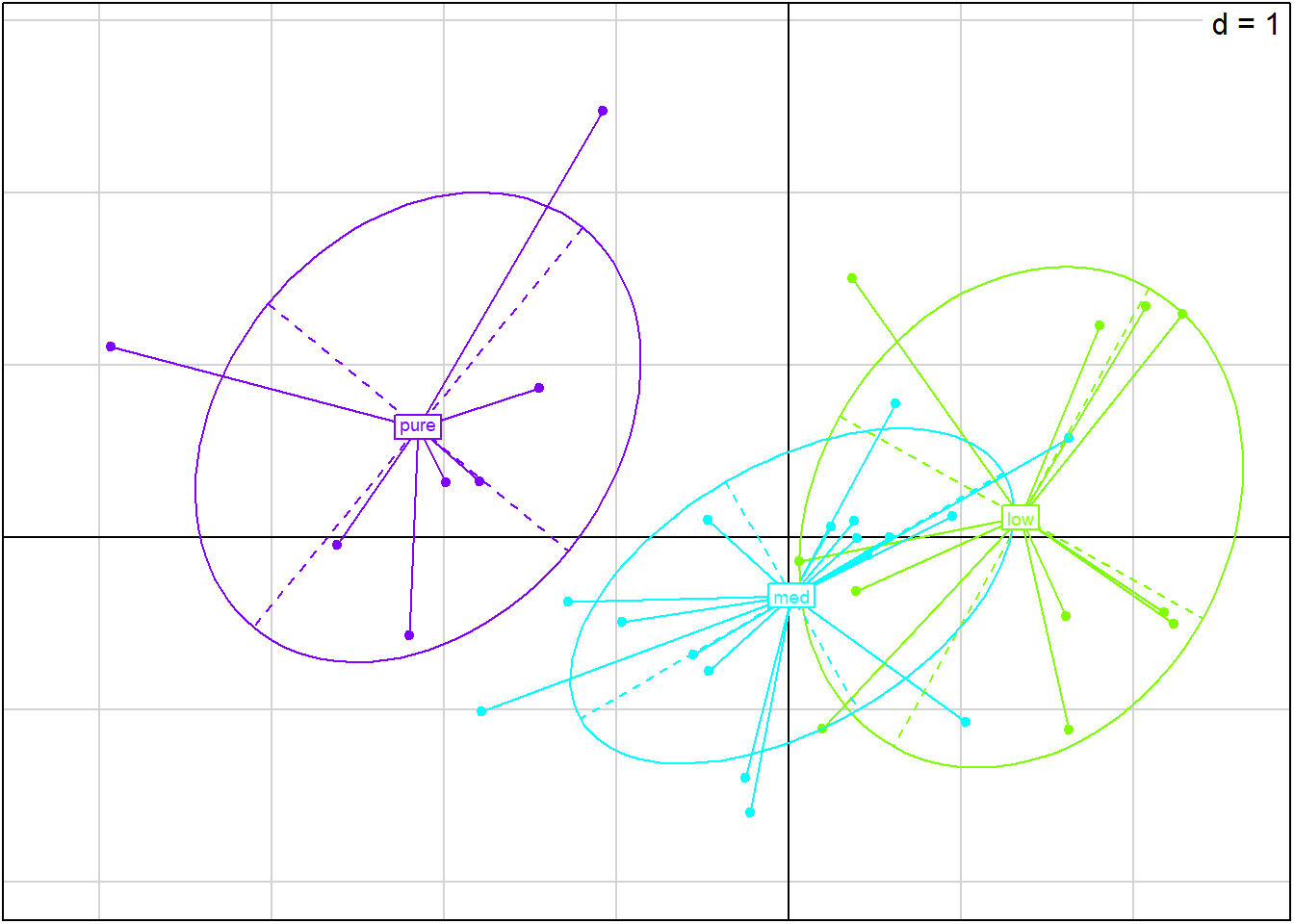
plot(acp, gg = T, cex.row = .6, col.row = 4,
     cex.col = .6, col.col = "darkgrey")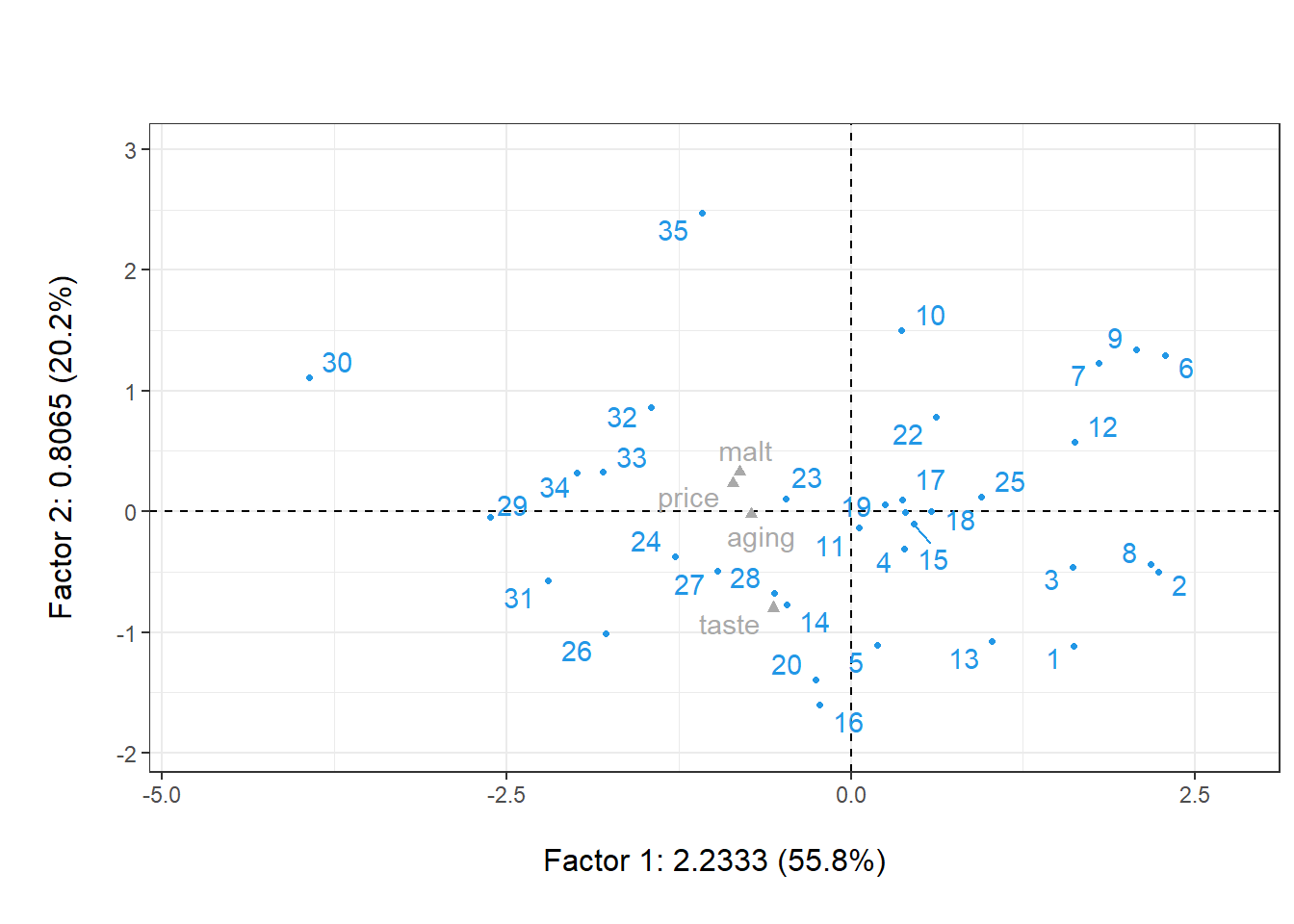

( sup <- supqual(acp, Whisky[, 3]) )

$wcat
   low    med   pure 
0.3143 0.4857 0.2000 

$dis2
   low    med   pure 
1.8445 0.1645 5.6113 

$coor
        Axis1   Axis2   Axis3    Axis4
low   1.34595  0.1174 -0.1214  0.06628
med   0.01583 -0.3391 -0.1630  0.15082
pure -2.15349  0.6389  0.5867 -0.47043

$tv
        Axis1  Axis2   Axis3   Axis4
low   3.55539  0.516 -0.6041  0.4549
med   0.06001 -2.139 -1.1643  1.4861
pure -4.20128  2.074  2.1559 -2.3849

$cos2
        Axis1    Axis2    Axis3    Axis4
low  0.982155 0.007472 0.007992 0.002382
med  0.001522 0.698702 0.161524 0.138251
pure 0.826463 0.072755 0.061343 0.039439

$scr
     Axis1  Axis2   Axis3   Axis4
qual 1.497 0.1418 0.08638 0.05669

ade4::s.class(acp$li, Whisky[, 3], clabel = .6, 
              col = rainbow(4)[2:4])

2.6 Taller (ACP de Lactantes)

if(!require(ISwR)){ # intenta cargar ISwR, si falla entonces
  install.packages("ISwR") # instala ISwR
  library(ISwR) # carga ISwR
}
data(kfm)
data <- kfm[, c(2,4:7)]
summary(data)

    dl.milk          weight        ml.suppl       mat.weight     mat.height 
 Min.   : 4.44   Min.   :4.12   Min.   :  0.0   Min.   :47.0   Min.   :153  
 1st Qu.: 6.55   1st Qu.:4.98   1st Qu.: 16.2   1st Qu.:55.0   1st Qu.:162  
 Median : 7.66   Median :5.35   Median : 57.5   Median :58.0   Median :167  
 Mean   : 7.50   Mean   :5.32   Mean   : 96.0   Mean   :60.0   Mean   :167  
 3rd Qu.: 8.43   3rd Qu.:5.64   3rd Qu.:103.8   3rd Qu.:64.5   3rd Qu.:172  
 Max.   :10.43   Max.   :6.58   Max.   :590.0   Max.   :80.0   Max.   :185

summary(kfm[, 3])

 boy girl 
  25   25

acp <- dudi.pca(data, scannf = FALSE, nf = n)

inertia_acp <- inertia(acp, row.inertia = TRUE, col.inertia = TRUE)
valp <- t(inertia_acp$tot.inertia) # valores propios
kable(valp, digits = 2)

	Ax1	Ax2	Ax3	Ax4	Ax5
inertia	2.47	1.07	0.74	0.44	0.27
cum	2.47	3.54	4.28	4.73	5.00
cum(%)	49.49	70.90	85.70	94.59	100.00

barplot(acp$eig, horiz = TRUE) # histograma de valores propios
abline(v = 1, lty = 3)

kable(inertia_acp$col.abs, digits = 1)

	Axis1	Axis2	Axis3	Axis4	Axis5
dl.milk	27.4	2.4	15.7	19.3	35.2
weight	24.4	0.7	33.5	16.4	25.0
ml.suppl	0.3	90.0	0.0	1.3	8.4
mat.weight	23.0	4.1	27.6	35.4	10.0
mat.height	24.9	2.8	23.3	27.5	21.4

kable(inertia_acp$col.rel, digits = 1)

	Axis1	Axis2	Axis3	Axis4	Axis5
dl.milk	-67.7	-2.6	11.6	8.6	-9.5
weight	-60.4	0.7	24.8	-7.3	6.8
ml.suppl	-0.8	96.4	0.0	-0.6	-2.3
mat.weight	-56.8	-4.3	-20.4	-15.7	-2.7
mat.height	-61.7	3.0	-17.2	12.2	5.8

s.corcircle(acp$co)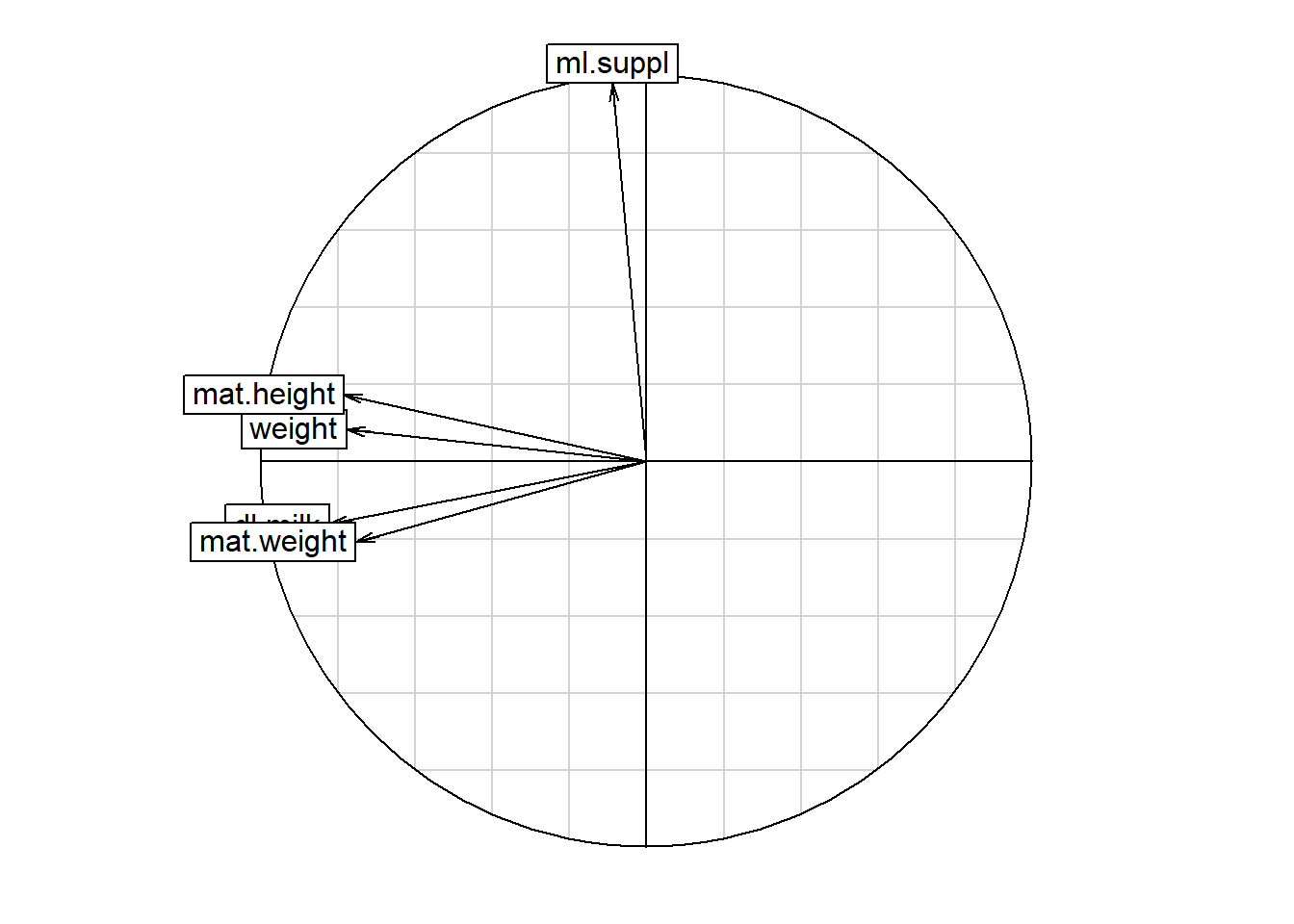

s.corcircle(acp$co, 3, 2)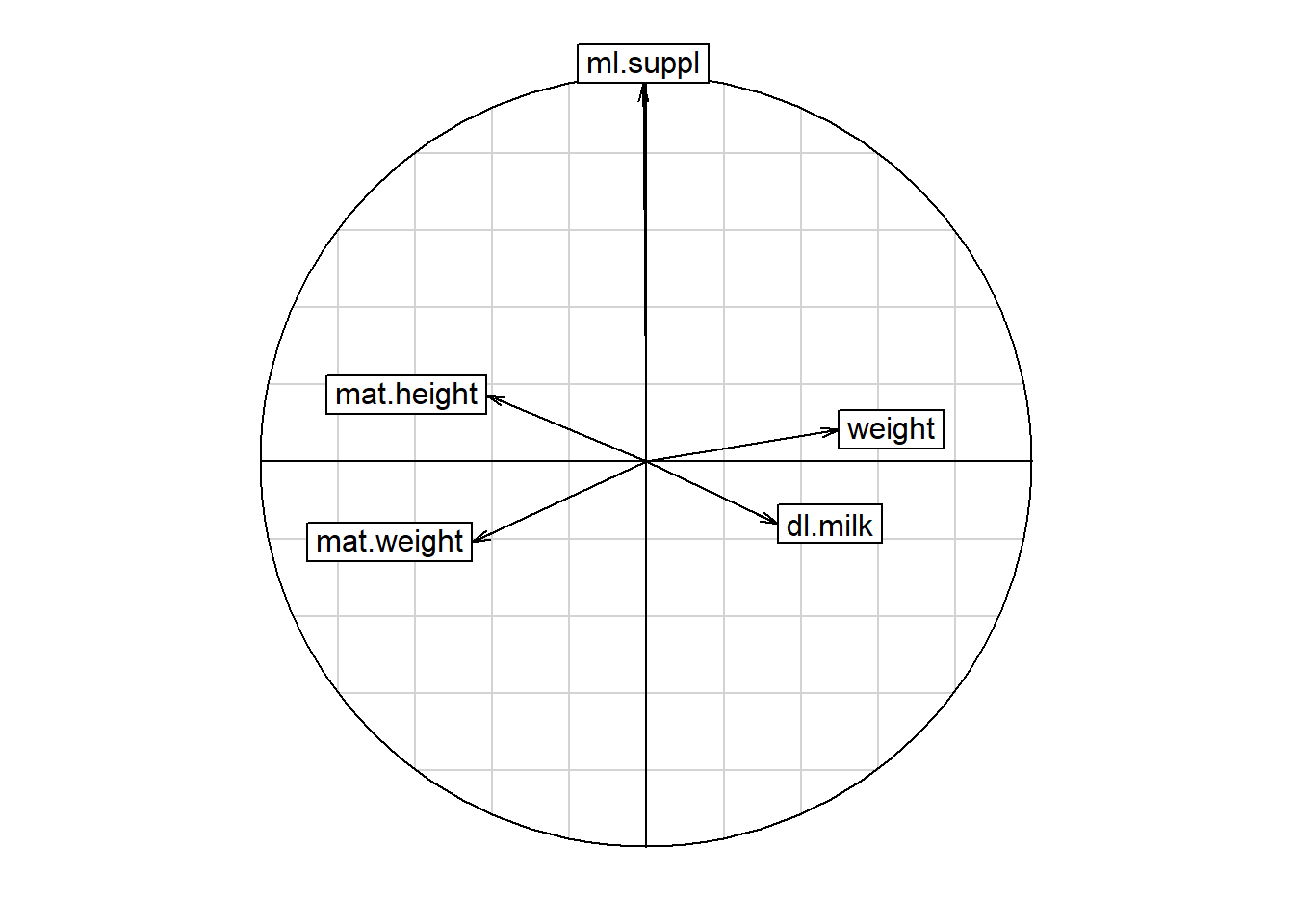

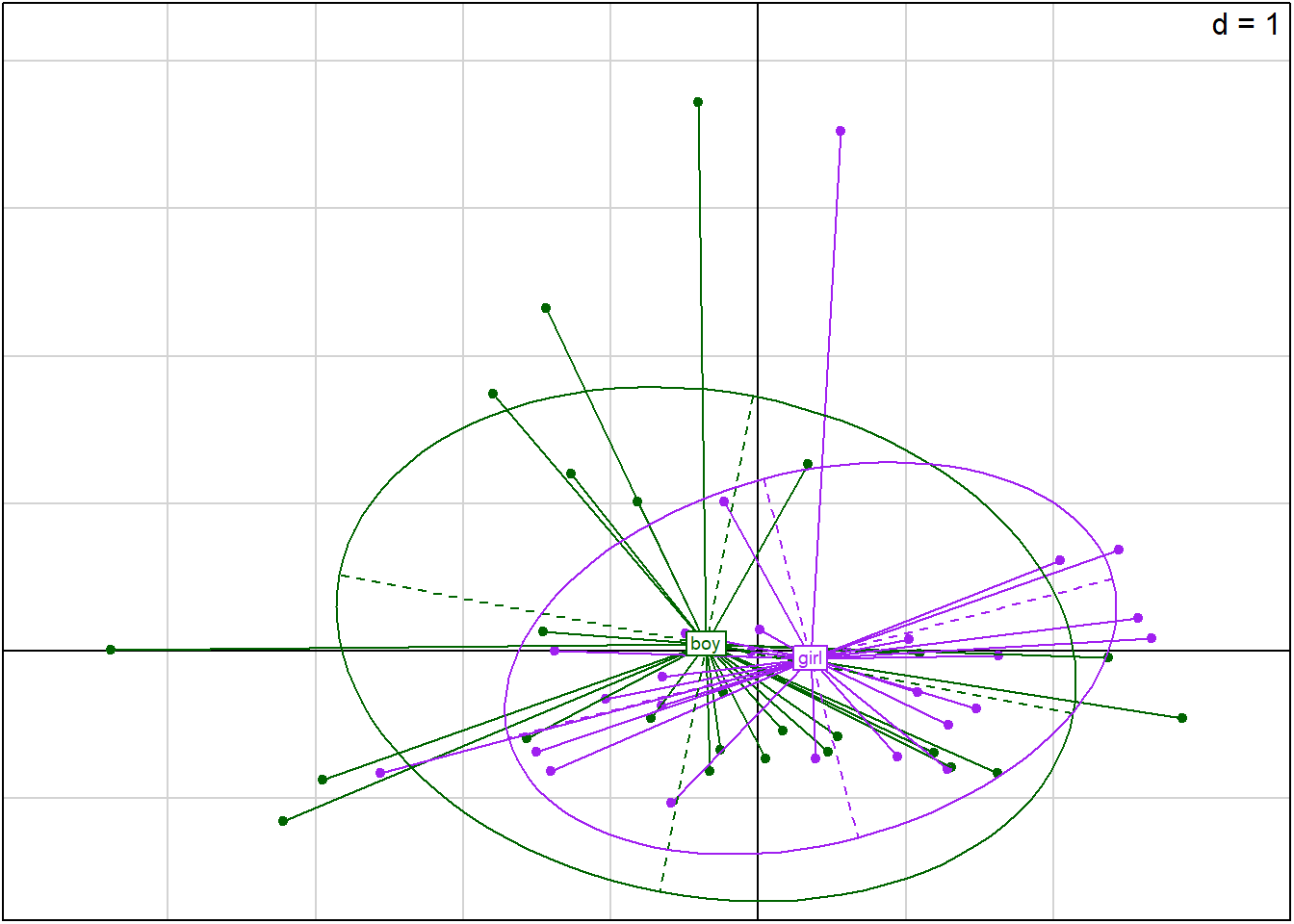
plot(acp, gg = T, cex.row = .5, col.row = 4,
     Tcol = FALSE)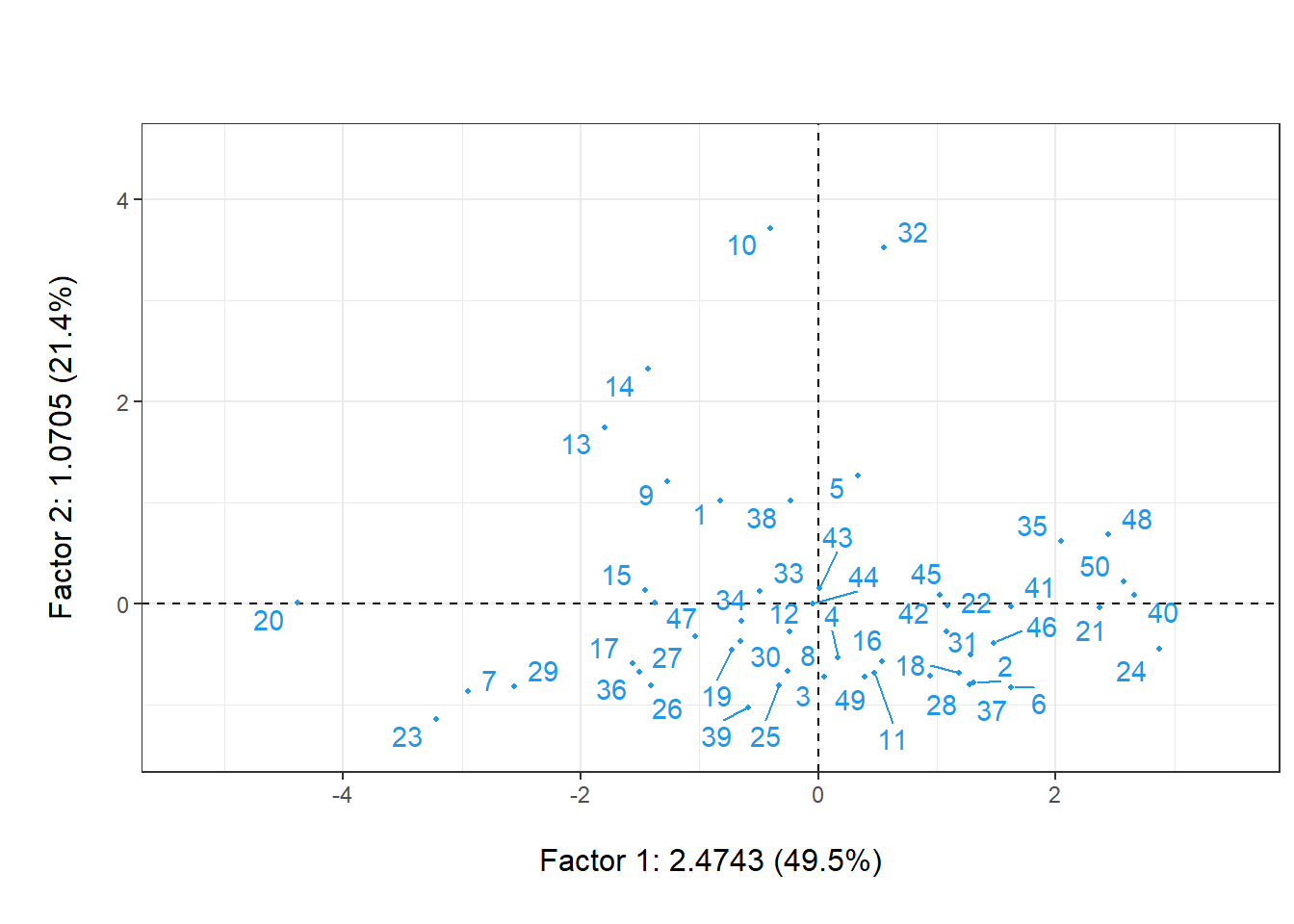

( sup <- supqual(acp, kfm[, 3]) )

$wcat
 boy girl 
 0.5  0.5 

$dis2
   boy   girl 
0.1598 0.1598 

$coor
       Axis1    Axis2   Axis3    Axis4   Axis5
boy  -0.3536  0.04806  0.1604  0.06465 -0.0506
girl  0.3536 -0.04806 -0.1604 -0.06465  0.0506

$tv
      Axis1   Axis2  Axis3   Axis4   Axis5
boy  -1.574  0.3252  1.306  0.6788 -0.6809
girl  1.574 -0.3252 -1.306 -0.6788  0.6809

$cos2
      Axis1   Axis2  Axis3   Axis4   Axis5
boy  0.7823 0.01445 0.1611 0.02616 0.01602
girl 0.7823 0.01445 0.1611 0.02616 0.01602

$scr
     Axis1   Axis2   Axis3   Axis4   Axis5
qual 0.125 0.00231 0.02574 0.00418 0.00256

ade4::s.class(acp$li, kfm[, 3], clabel = .6, 
              col = c("darkgreen","purple"))