3 Bivariada
En esta sección se hará una revisión de algunos temas relacionados con el análisis descriptivo de datos de dos variables.
- Lea todo el contenido de la presente sección (Estadística Descriptiva, 2 Bivariada).
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
El siguiente ejercicio se plantea una situación en donde se tienen varias variables.
Ejercicio 3.1
McGivern Jewelers se ubica en Levis Square Mall, justo al sur de Toledo, Ohio. Recién publicó un anuncio en el periódico local en el que indicaba la forma, el tamaño, el precio y el grado de corte de 33 de sus diamantes en existencia.
Lind, Marchal & Wathen (2012). Estadistica Aplicada a los Negocios y la Economia. (15a. ed.) McGraw-Hill. Capítulo 4, Ejercicio 37.
Los datos asociados a las cuatro variables de los 33 diamantes se encuentran en la pestaña “Datos” de la hoja de cálculo (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
¿Después de trabajar con cada variable por separado, se puede trabajar con más de una variable a la vez? ¿qué se gana al poder trabajar “conjuntamente” con más de una variable, con respecto a trabajarlas cada una por separado? ¿en qué consistiría el hacer estadística descriptiva “conjuntamente” con más de una variable?
3.1 Tablas de contingencia
Una tabla de contingencia es una representación tabular que presenta simultáneamente las frecuencias de los valores/categorías que toman dos variables.
3.1.1 Tabla de frecuencias absolutas conjuntas
Una tabla de frecuencias absolutas conjuntas tiene la siguiente estructura:
| \, | A\,1 | \cdots | A\,s | Total |
|---|---|---|---|---|
| B\,1 | f_{11} | \cdots | f_{1s} | \sum_{j=1}^{s} f_{1j} = f_{1 \cdotp} |
| \vdots | \vdots | \ddots | \vdots | \vdots |
| B\,r | f_{r1} | \cdots | f_{rs} | \sum_{j=1}^{s} f_{rj} = f_{r \cdotp} |
| Total | \sum_{i=1}^{r} f_{i1} = f_{\cdotp 1} | \cdots | \sum_{i=1}^{r} f_{is} = f_{\cdotp s} | f_{\cdotp \cdotp} = N |
A\,1, \dots, A\,s: etiquetas, valores o intervalos asociados a la primera variable.
B\,1, \dots, B\,r: etiquetas, valores o intervalos asociados a la segunda variable.
Ejercicio 3.2 Retomando el Ejercicio 3.1 acerca de los 33 diamantes con sus cuatro variables, ¿cuáles serían las representaciones tabulares y gráficas de las frecuencias absolutas conjuntas para las variables Forma y Grado de corte?
Las representaciones tabulares y gráficas de las frecuencias absolutas conjuntas para las variables Forma y Grado de corte se pueden observar en las pestañas “FrecAbs1” y “FrecAbs2” de la hoja de cálculo (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
3.1.2 Tabla de frecuencias relativas conjuntas
Una tabla de frecuencias relativas conjuntas tiene la siguiente estructura:
| \, | A\,1 | \cdots | A\,s | Total |
|---|---|---|---|---|
| B\,1 | \frac{f_{11}}{N} | \cdots | \frac{f_{1s}}{N} | \frac{f_{1 \cdotp}}{N} |
| \vdots | \vdots | \ddots | \vdots | \vdots |
| B\,r | \frac{f_{r1}}{N} | \cdots | \frac{f_{rs}}{N} | \frac{f_{r \cdotp}}{N} |
| Total | \frac{f_{\cdotp 1}}{N} | \cdots | \frac{f_{\cdotp s}}{N} | \frac{N}{N} = 1 |
A\,1, \dots, A\,s: etiquetas, valores o intervalos asociados a la primera variable.
B\,1, \dots, B\,r: etiquetas, valores o intervalos asociados a la segunda variable.
Ejercicio 3.3 Retomando el Ejercicio 3.1 acerca de los 33 diamantes con sus cuatro variables, ¿cuáles serían las representaciones tabulares y gráficas de las frecuencias relativas conjuntas para las variables Forma y Grado de corte?
Las representaciones tabulares y gráficas de las frecuencias relativas conjuntas para las variables Forma y Grado de corte se pueden observar en la pestaña “FrecRel2” de la hoja de cálculo (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
3.1.3 Tabla de perfiles fila
Ejercicio 3.4 Supongamos que cada manzana de la ciudad de Bogotá es un individuo o unidad estadística. Cada uno de nuestros individuos va a tener un valor para la variable Localidad y uno para la variable Estrato socioeconómico (cada manzana se encuentra en una localidad de Bogotá y tiene asociado un estrato socioeconómico).
Una tabla de contingencia de frecuencias absolutas conjuntas para las variables Localidad y Estrato socioeconómico se encuentran en la pestaña “Estrato y localidad manzanas” de la hoja de cálculo (Google Sheets): EjemploPerfilesFilaTablaContingenciasLocalidadesEstratos.gsheet
¿Existe alguna manera de mostrar e identificar qué localidades de Bogotá se parecen en cuanto a la forma en que están “repartidos” en ellas los estratos socioeconómicos?
Una tabla de perfiles fila tiene la siguiente estructura:
| \, | A\,1 | \cdots | A\,s | Total |
|---|---|---|---|---|
| B\,1 | \frac{f_{11}}{f_{1 \cdotp}} | \cdots | \frac{f_{1s}}{f_{1 \cdotp}} | \frac{f_{1 \cdotp}}{f_{1 \cdotp}} = 1 |
| \vdots | \vdots | \ddots | \vdots | \vdots |
| B\,r | \frac{f_{r1}}{f_{r \cdotp}} | \cdots | \frac{f_{rs}}{f_{r \cdotp}} | \frac{f_{r \cdotp}}{f_{r \cdotp}} = 1 |
| Total | \frac{f_{\cdotp 1}}{f_{\cdotp \cdotp}} | \cdots | \frac{f_{\cdotp s}}{f_{\cdotp \cdotp}} | \frac{N}{N} = 1 |
A\,1, \dots, A\,s: etiquetas, valores o intervalos asociados a la primera variable.
B\,1, \dots, B\,r: etiquetas, valores o intervalos asociados a la segunda variable.
Ejercicio 3.5 Retomando el Ejercicio 3.1 acerca de los 33 diamantes con sus cuatro variables, ¿cuáles serían las representaciones tabulares y gráficas de los perfiles fila para la variable Grado de corte con respecto a la variable Forma?
Las representaciones tabulares y gráficas de los perfiles fila para la variable Grado de corte con respecto a la variable Forma se pueden observar en la pestaña “PerfilFil” (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
Ejercicio 3.6 Retomando el Ejercicio 3.4 acerca de las manzanas en Bogotá con su respectiva localidad y estrato socioeconómico, ¿cuáles serían las representaciones tabulares y gráficas de los perfiles fila para la variable Localidad con respecto a la variable Estrato socioeconómico?
Las representaciones tabulares y gráficas de los perfiles fila para la variable Localidad con respecto a la variable Estrato socioeconómico se pueden observar en las pestañas “Tabla Perfiles Fila” y “Grafico Perfiles Fila” (Google Sheets): EjemploPerfilesFilaTablaContingenciasLocalidadesEstratos.gsheet
3.1.4 Tabla de perfiles columna
| \, | A\,1 | \cdots | A\,s | Total |
|---|---|---|---|---|
| B\,1 | \frac{f_{11}}{f_{\cdotp 1}} | \cdots | \frac{f_{1s}}{f_{\cdotp s}} | \frac{f_{1 \cdotp}}{f_{\cdotp \cdotp}} |
| \vdots | \vdots | \ddots | \vdots | \vdots |
| B\,r | \frac{f_{r1}}{f_{\cdotp 1}} | \cdots | \frac{f_{rs}}{f_{\cdotp s}} | \frac{f_{r \cdotp}}{f_{\cdotp \cdotp}} |
| Total | \frac{f_{\cdotp 1}}{f_{\cdotp 1}} = 1 | \cdots | \frac{f_{\cdotp s}}{f_{\cdotp s}} = 1 | \frac{N}{N} = 1 |
A\,1, \dots, A\,s: etiquetas, valores o intervalos asociados a la primera variable.
B\,1, \dots, B\,r: etiquetas, valores o intervalos asociados a la segunda variable.
Ejercicio 3.7 Retomando el Ejercicio 3.1 acerca de los 33 diamantes con sus cuatro variables, ¿cuáles serían las representaciones tabulares y gráficas de los perfiles columna para la variable Forma con respecto a la variable Grado de corte?
Las representaciones tabulares y gráficas de los perfiles columna para la variable Forma con respecto a la variable Grado de corte se pueden observar en la pestaña “PerfilCol” (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
En el siguiente enlace, en la pestaña “Two Categorical Variables”, encontrarán más ejemplos: https://istats.shinyapps.io/EDA_categorical/
3.2 Diagrama de dispersión
Diagrama de dispersión: Representación gráfica que muestra simultáneamente los datos de dos variables mediante el uso de un plano cartesiano.
A continuación se muestran tres registros de un conjunto de datos asociado a un estudio histórico muy famoso que realizó Karl Pearson, acerca de la capacidad de heredar la estatura. Pearson midió la estatura de 1078 padres (fheight) junto con la estatura de sus respectivos hijos adultos (sheight). Los datos originales fueron medidos y reportados a la pulgada más cercana. A dichos datos, posteriormente se les adicionó un pequeña magnitud aleatoria uniforme para que resaltar que estatura debe considerarse como una variable continua y no como una variable discreta.
| \, | fheight | sheight |
|---|---|---|
| 1 | 65.04851 | 59.77827 |
| 2 | 63.25094 | 63.21404 |
| \vdots | \vdots | \vdots |
| 1078 | 65.62374 | 70.51318 |
El gráfico de dispersión de las 1078 estaturas de padres e hijos se muestra a continuación:
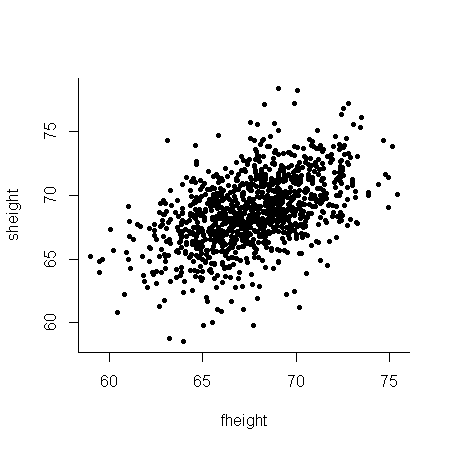
Ejercicio 3.8 Retomando el Ejercicio 3.1 acerca de los 33 diamantes con sus cuatro variables, ¿cuál sería el diagrama de dispersión para las variables Tamaño y Precio?
El diagrama de dispersión para las variables Tamaño y Precio se puede observar en la pestaña “DiagrDispers” (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
3.3 Medidas de relación entre dos variables cuantitativas
¿El aumento o disminución de los valores de una variable está relacionado con el aumento o disminución de los valores de la otra? ¿Se puede establecer una medida que dé cuenta de esa potencial relación entre variables?
Covarianza: La covarianza es una medida descriptiva o medida resumen que nos indica si es posible que exista una relación lineal entre dos variables y si esta es directa o inversa.
\begin{aligned} \sigma_{xy} &= \frac{1}{N} \sum_{i=1}^{N} \left(x_i - \mu_x\right) \left(y_i - \mu_y\right) \\ &= \frac{1}{N} \sum_{i=1}^{N} x_i y_i - \mu_x \mu_y \end{aligned}
¿Qué “expresa” la fórmula de la covarianza? ¿qué representa geométricamente o cuál es la interpretación geométrica de la fórmula de la covarianza?
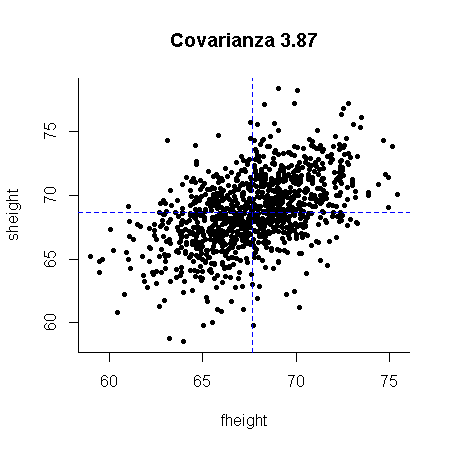
- \sigma_{xy} > 0, Indica una potencial relación lineal directa o positiva.
- \sigma_{xy} = 0, Indica que no hay relación lineal.
- \sigma_{xy} < 0, Indica una potencial relación lineal inversa o negativa.
Coeficiente de correlación de Pearson: Es una medida que indica el tipo y el nivel o grado de la relación lineal entre dos variables (excluyendo rectas horizontales y verticales).
\begin{aligned} \rho = \frac{\sigma_{xy}}{\sigma_x \sigma_y} &= \frac{\frac{1}{N}\sum_{i=1}^{N} \left(x_i - \mu_x\right) \left(y_i - \mu_y\right)}{\sqrt{\frac{1}{N}\sum_{i=1}^{N} \left(x_i - \mu_x\right)^2} \sqrt{\frac{1}{N}\sum_{i=1}^{N} \left(y_i - \mu_y\right)^2}} \\ &= \frac{\frac{1}{N} \sum_{i=1}^{N} x_i y_i - \mu_x \mu_y}{\sqrt{\frac{1}{N} \sum_{i=1}^{N} x_i^2 - \mu_x^2} \sqrt{\frac{1}{N} \sum_{i=1}^{N} y_i^2 - \mu_y^2}} \\ &= \frac{\sum_{i=1}^{N} x_i y_i - N \mu_x \mu_y}{\sqrt{\sum_{i=1}^{N} x_i^2 - N \mu_x^2} \sqrt{\sum_{i=1}^{N} y_i^2 - N \mu_y^2}} \end{aligned}
¿En que unidades está \rho? ¿qué tiene que ocurrir para que \rho = 0? ¿qué pasa cuando y_i = a + b x_i para todo i?
Explorar el contenido de los siguientes enlaces podría ayudar a resolver las anteriores preguntas:
- El coeficiente de correlación de Pearson \rho es adimensional (no tiene unidades).
- \rho toma valores entre -1 y 1.
- \rho tiene el mismo signo que la covarianza, por lo tanto el signo nos indica si hay relación lineal directa (\rho > 0), inversa (\rho < 0), o si no hay relación lineal (\rho = 0).
- Si la relación es lineal directa exacta entonces \rho = 1, si es inversa exacta entonces \rho=-1.
- Cuanto más se acerca \rho a 1 o a -1, mayor es el nivel, grado o fuerza de la relación lineal. Entre más se acerque a 0 más débil es la relación lineal.
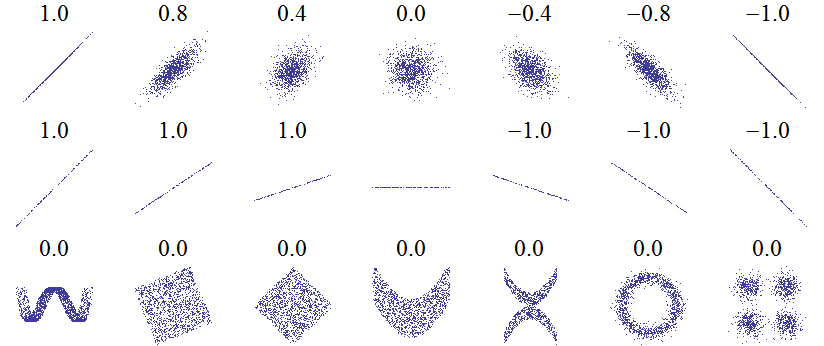
Diferentes autores han dado guías para la interpretación de la magnitud \rho. Sin embargo los criterios de dichas guías no dejan de ser arbitrarios. La interpretación del coeficiente de correlación depende tanto del contexto como del objetivo detrás de su obtención. Por otra parte, \rho^2 puede inicialmente pensarse como una proporción asociada al grado de la relación lineal entre las variables (que al multiplicarla por cien se traduce en un porcentaje).
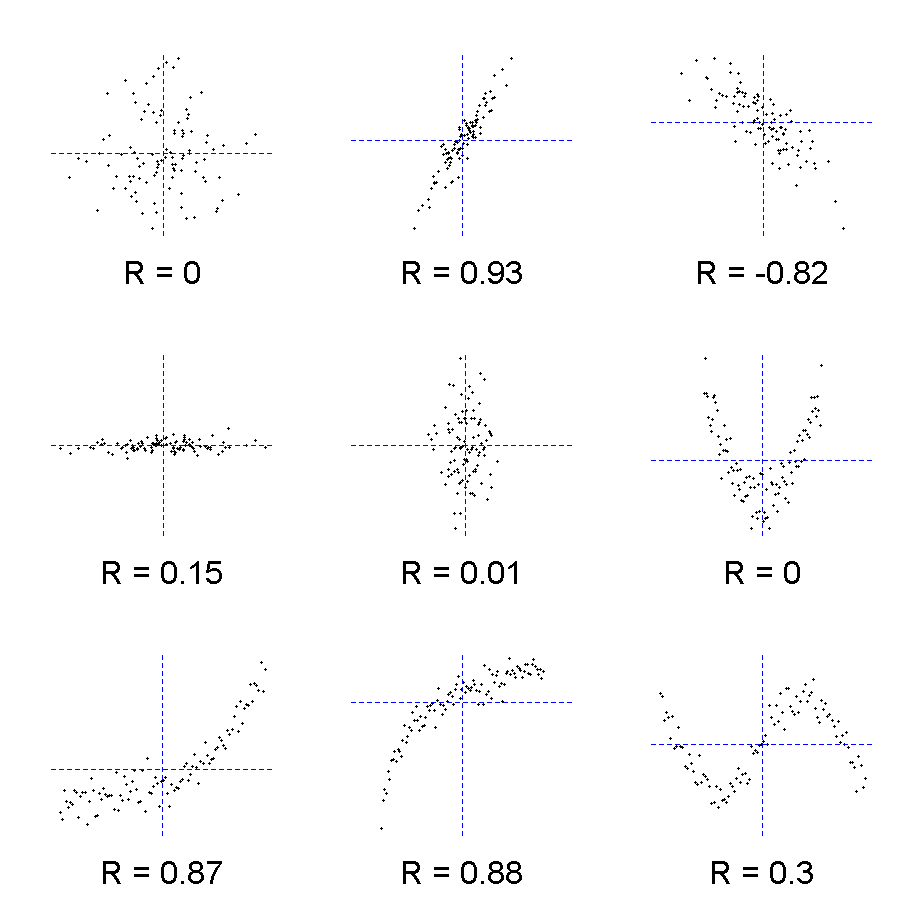
En el siguiente enlace encontrará un juego que consiste en adivinar la correlación (Correlation Game): https://gallery.shinyapps.io/correlation_game/
3.4 La recta que mejor ajusta
Si dos variables tienen en alguna medida una relación lineal, es lógico que nos preguntemos: ¿cuál es la ecuación de la recta que mejor representa dicha relación?, o en otras palabras, ¿cuál es la recta que mejor se ajusta a los datos de las dos variables?
Explorar el contenido del siguiente enlace podría ayudar a resolver las anteriores preguntas: https://www.rossmanchance.com/applets/2021/regshuffle/regshuffle.htm
La ecuación de la recta que relaciona a una variable x con una variable y se escribe así:
y = \beta_0 + \beta_1 x
en donde \beta_0 representa el intercepto y \beta_1 representa la pendiente de la recta.
Ahora, queremos encontrar valores para \beta_0 y \beta_1 tales que minimicen la función: g(\beta_0,\beta_1) = \sum_{i=1}^{n} e^2_i donde e_i = y_i - f(x_i) y f(x_i) = \beta_0 + \beta_1 x_i, es decir, queremos encontrar valores para \beta_0 y \beta_1 que minimicen: g(\beta_0,\beta_1) = \sum_{i=1}^{n} \left(y_i - \left(\beta_0 + \beta_1 x_i\right)\right)^2
Usando derivadas parciales, igualando a cero y solucionando el sistema de ecuaciones resultante, se obtiene que: \begin{aligned} \beta_1 &= \frac{\sigma_{xy}}{\sigma_x^2} = \rho \frac{\sigma_y}{\sigma_x} = b \\ \beta_0 & = \mu_y - \beta_1 \mu_x = a \end{aligned}
Los valores \beta_0 = a y \beta_1 = b son los que minimizan los “errores” al cuadrado (distancias “verticales” entre los valores observados para la variable y y los valores que se obtendrían al usar la ecuación de la recta sobre los valores de la variable x). La anterior manera de encontrar la recta que mejor ajusta corresponde al denominado método de mínimos cuadrados.
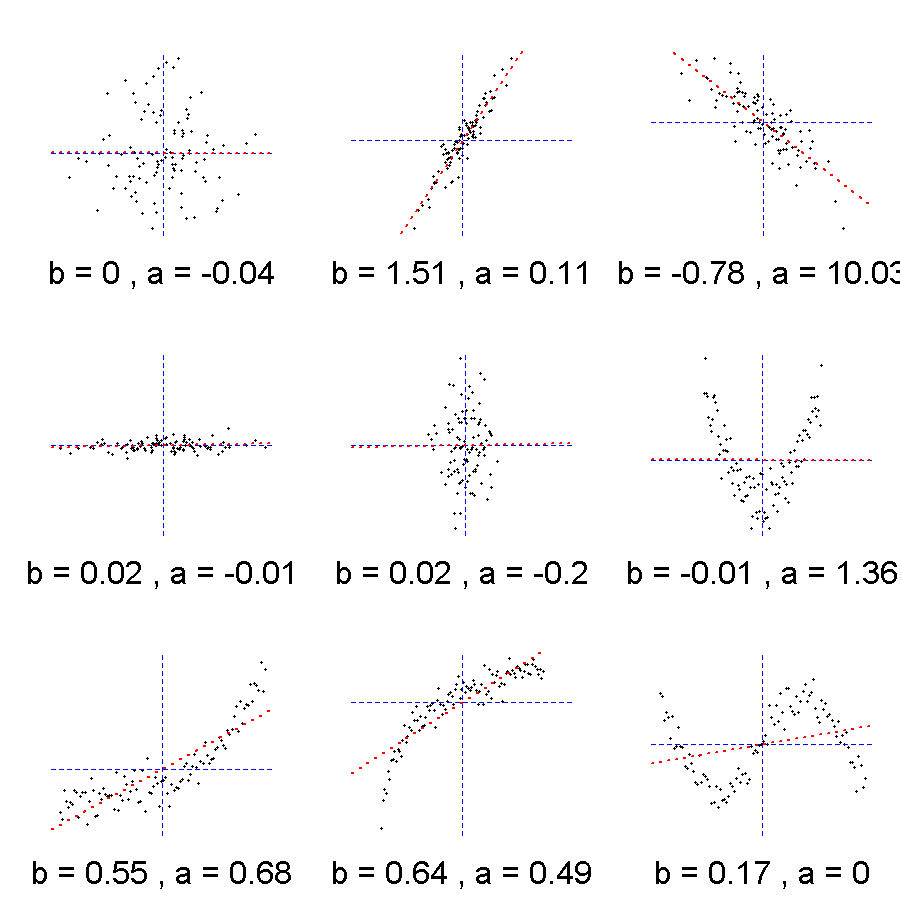
En la siguiente hoja de cálculo (Google Sheets) encontrarán un ejemplo relacionado con el cálculo de covarianza, coeficiente de correlación, intercepto y pendiente (del ajuste por mínimos cuadrados): EjemploCalculosMedidasDescriptivasDosVariablesContinuas.gsheet
No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios del capítulo 3 del libro de Mendenhall o de las secciones 2.3, 2.4 y 3.5 del libro de Anderson.
Aprenda a usar su calculadora para obtener ágilmente: \mu_x (media de X), \mu_y (media de Y), \sigma_x (desviación estándar de X), \sigma_y (desviación estándar de Y), \rho (correlación entre X y Y), b (pendiente de la recta ajustada) y a (intercepto de la recta ajustada). (\sigma_{xy} se puede calcular a partir de \sigma_x, \sigma_y y \rho).
Suponga que y_i = a + bx_i para todo i. Deduzca analíticamente que:
- \mu_y = a + b \mu_x
- \rho = 1 cuando b > 0
- \rho = -1 cuando b < 0