4 Fund. matemáticos
Conceptos básicos clave y fundamentos matemáticos
Pero… ¿PARA QUÉ SIRVEN LAS MATEMÁTICAS? (Derivando - Apr 13, 2022 - 8:28)
4.1 ¿Objetos matemáticos importantes relacionados con los datos?
Retomemos nuevamente la tabla de datos de países, pero en este caso conservemos únicamente las variables cuantitativas:
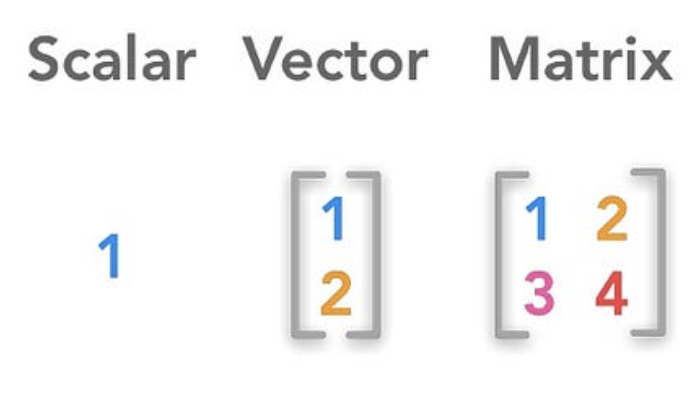
En cada celda de la tabla hay un número, también llamado escalar, un objeto matemático fundamental. No solo eso, toda una fila o toda una columna se pueden ver como un objeto matemático “compuesto” llamado vector. Así mismo, toda la tabla se puede ver como otro objeto matemático llamado matriz.
4.1.1 ¿Los números (los escalares)?
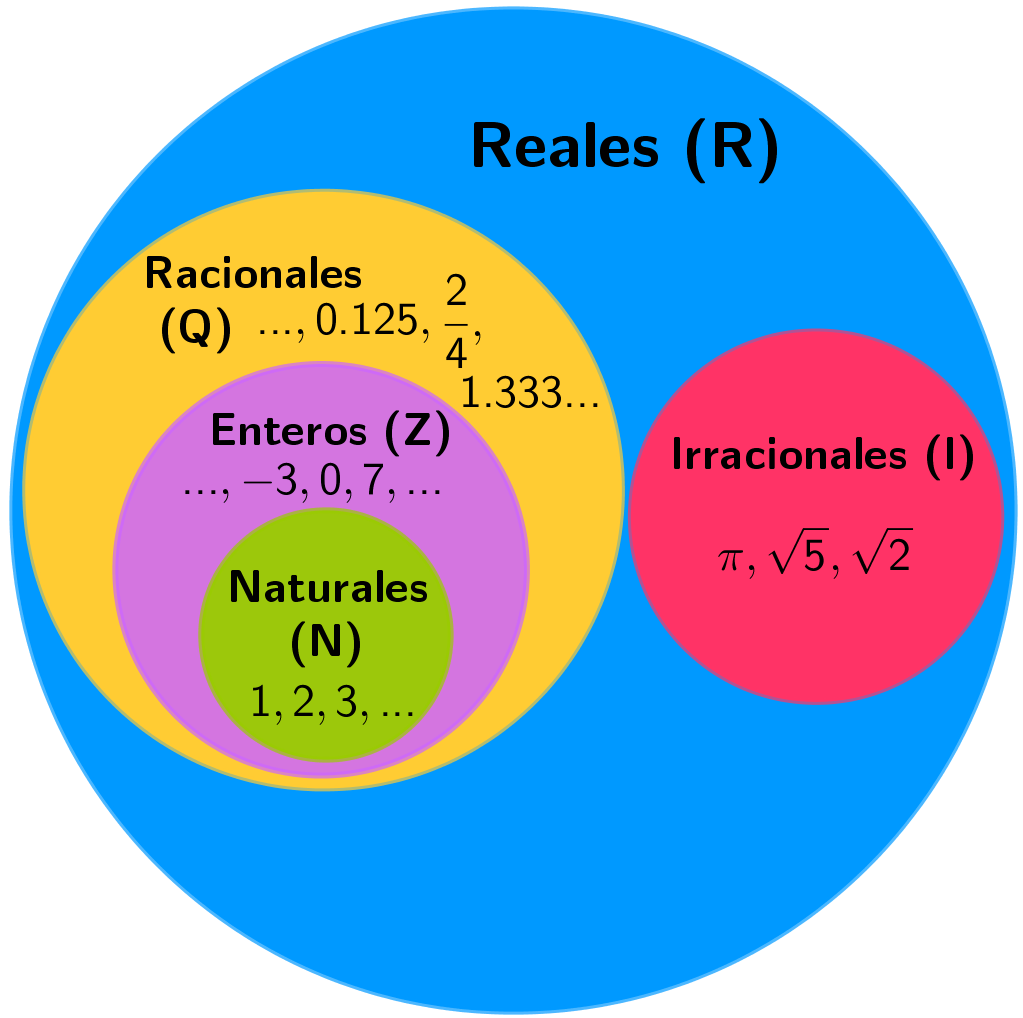
Hay de varios tipos distintos:
Los números naturales \left( \mathbb{N} \right)
Los números enteros \left( \mathbb{Z} \right)
Los números racionales \left( \mathbb{Q} \right)
Los números irracionales \left( \mathbb{I} \right)
Los números reales \left( \mathbb{R} \right)
4.1.2 ¿Vectores?
Un punto en el plano cartesiano queda totalmente determinado por una pareja ordenada de números reales. Las duplas se llaman vectores de tamaño 2 y los elementos de las duplas se llaman componentes del vector.
Sean \mathbf{x}=(x_1,x_2) y \mathbf{y}=(y_1,y_2), se definen dos operaciones.
-
Suma:
\mathbf{x}+\mathbf{y}=(x_1+y_1,x_2+y_2)
Ejemplo:
(1,2)+(1,3)=(1+1,2+3)=(2,5)
-
Multiplicación por escalar:
c \, \mathbf{x} = (c \, x1, c\, x2).
Ejemplo:
3 \, \mathbf{x} = 3 \, (1,2)=(3,6)
En Estadística solemos escribir los vectores como columnas, ya que tienden a representar los valores que toma una variable para un conjunto de individuos.
¿Cómo usar las operaciones?:
Si tenemos 4 vectores,
\mathbf{x}_1=\left[\begin{array}{l} 1 \\ 2 \end{array}\right], \mathbf{x}_2=\left[\begin{array}{l} 1 \\ 3 \end{array}\right], \mathbf{x}_3=\left[\begin{array}{l} 3 \\ 4 \end{array}\right], \mathbf{x}_4=\left[\begin{array}{l} 3 \\ 2 \end{array}\right]
Podemos sumar los 4 vectores:
\begin{aligned} \left[\begin{array}{l} 1 \\ 2 \end{array}\right]+\left[\begin{array}{l} 1 \\ 3 \end{array}\right]+\left[\begin{array}{l} 3 \\ 4 \end{array}\right]+\left[\begin{array}{l} 3 \\ 2 \end{array}\right] &= \left[\begin{array}{l} 1+1+3+3 \\ 2+3+4+2 \end{array}\right] \\ &= \left[\begin{array}{l} 8 \\ 11 \end{array}\right] \end{aligned}
Si multiplicamos el vector suma por \frac{1}{4}=0.25 obtenemos el vector promedio de los 4 vectores:
\frac{1}{4}\left[\begin{array}{l} 8 \\ 11 \end{array}\right]=\left[\begin{array}{l} 2 \\ 2.75 \end{array}\right]
4.1.3 ¿Matrices?
Con matrices podemos seguir los mismos pasos,
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} + \begin{bmatrix} 4 & 2 \\ 1 & 3 \\ \end{bmatrix} = \begin{bmatrix} 1+4 & 2+2 \\ 3+1 & 4+3 \\ \end{bmatrix}= \begin{bmatrix} 5 & 4 \\ 4 & 7 \\ \end{bmatrix}
2\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 2\times 1 & 2\times 2 \\ 2 \times3 & 2 \times 4 \\ \end{bmatrix}= \begin{bmatrix} 2 & 4 \\ 6 & 8 \\ \end{bmatrix}
Se dice que las matrices de este ejemplo son de tamaño 2 \times 2, lo cual quiere decir que son de 2 filas y 2 columnas.
¿Cómo lo usamos y para qué nos podría servir?
Imaginemos que tenemos 3 tablas, cada una tiene pagos que 5 personas realizaron por gas y luz, durante los meses de enero, febrero y marzo, respectivamente
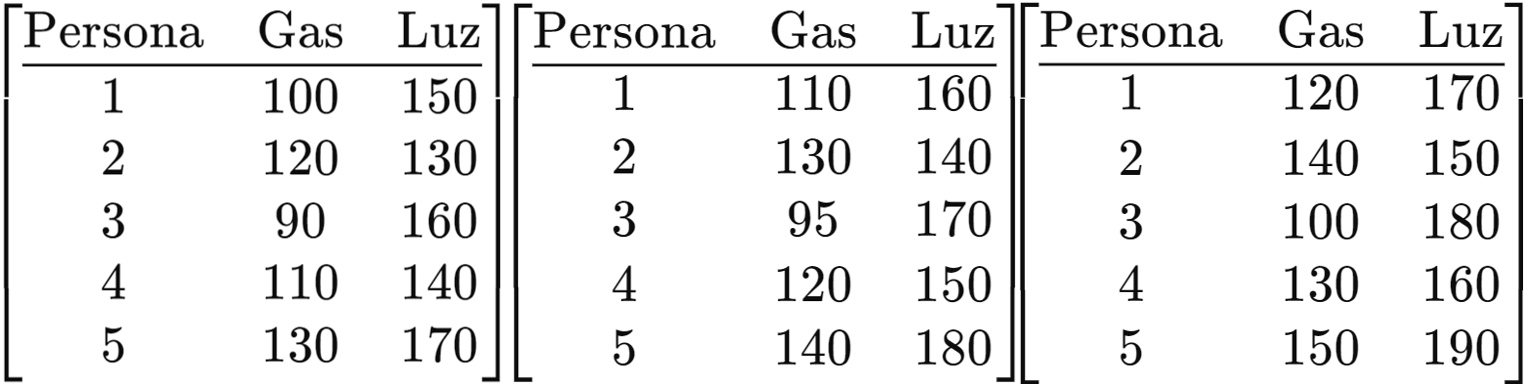
Esto lo podemos ver como 3 matrices para realizar un análisis:
\begin{bmatrix} 100 & 150 \\ 120 & 130 \\ 90 & 160 \\ 110 & 140 \\ 130 & 170 \\ \end{bmatrix}, \begin{bmatrix} 110 & 160 \\ 130 & 140 \\ 95 & 170 \\ 120 & 150 \\ 140 & 180 \\ \end{bmatrix}, \begin{bmatrix} 120 & 170 \\ 140 & 150 \\ 100 & 180 \\ 130 & 160 \\ 150 & 190 \\ \end{bmatrix}
Si sumamos las 3 matrices, podemos ver el total de lo que las personas gastaron en estos 2 servicios durante el primer trimestre del año
\begin{bmatrix} 100 & 150 \\ 120 & 130 \\ 90 & 160 \\ 110 & 140 \\ 130 & 170 \\ \end{bmatrix}+ \begin{bmatrix} 110 & 160 \\ 130 & 140 \\ 95 & 170 \\ 120 & 150 \\ 140 & 180 \\ \end{bmatrix}+ \begin{bmatrix} 120 & 170 \\ 140 & 150 \\ 100 & 180 \\ 130 & 160 \\ 150 & 190 \\ \end{bmatrix}= \begin{bmatrix} 330 & 480 \\ 390 & 420 \\ 285 & 510 \\ 360 & 450 \\ 420 & 540 \\ \end{bmatrix}
Ahora, si eso lo multiplicamos por \frac{1}{3}:
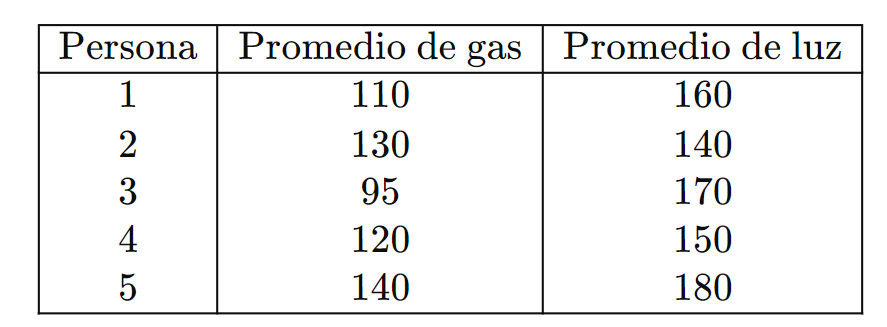
\frac{1}{3}\begin{bmatrix} 330 & 480 \\ 390 & 420 \\ 285 & 510 \\ 360 & 450 \\ 420 & 540 \\ \end{bmatrix}=\begin{bmatrix} 110 & 160 \\ 130 & 140\\ 95 & 170 \\ 120 & 150 \\ 140 & 180 \\ \end{bmatrix}
Obtenemos el gasto promedio de cada persona en gas y luz:
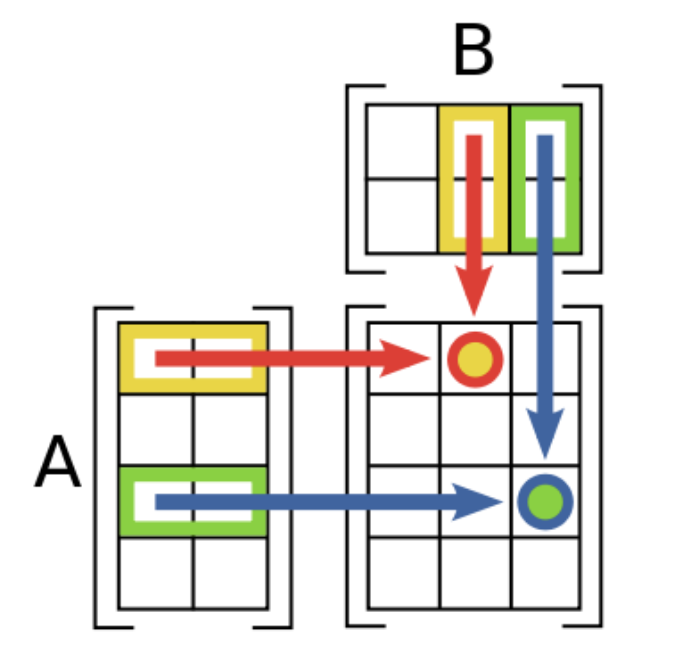
¿Si existe la suma de matrices, existe la multiplicación de matrices?
Veamos cómo se define la multiplicación de dos matrices. Una primera matriz \left(\mathbf{A}\right) se multiplica por una segunda matriz \left(\mathbf{B}\right) y el resultado es una tercera matriz \left(\mathbf{C}\right)
Sean
\mathbf{A}=\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right], \mathbf{B}=\left[\begin{array}{cc} 5 & 10 \\ 20 & 30 \end{array}\right]
Entonces se tiene que
\begin{aligned} \mathbf{A B} &= \left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right]\left[\begin{array}{cc} 5 & 10 \\ 20 & 30 \end{array}\right] \\ &=\left[\begin{array}{cc} 1 \times 5+2 \times 20 & 1 \times 10+2 \times 30 \\ 3 \times 5+4 \times 20 & 3 \times 10+4 \times 30 \end{array}\right] \\ &=\left[\begin{array}{cc} 45 & 70 \\ 95 & 150 \end{array}\right] = \mathbf{C} \end{aligned}
¿Cómo lo usamos y para qué nos podría servir?
Ejercicio 4.1 Una profesora tiene dos estudiantes que realizaron tres actividades evaluativas con calificación: examen, proyecto y presentación.
Las notas obtenidas fueron:
| Estudiante | Examen | Proyecto | Presentación |
|---|---|---|---|
| Estudiante 1 | 4.2 | 4.5 | 3.8 |
| Estudiante 2 | 3.9 | 4.0 | 4.3 |
Se están considerando dos posibles esquemas de ponderación para las actividades:
| Esquema | Examen | Proyecto | Presentación |
|---|---|---|---|
| Esquema A | 40% | 35% | 25% |
| Esquema B | 30% | 50% | 20% |
Calcule la nota definitiva de cada estudiante bajo cada esquema de ponderación.
4.2 ¿El método científico y los modelos?
Objetivo: Resolver problemas de interés en un área mediante la aplicación eficiente de principios científicos.
- Describir el problema o fenómeno.
- Identificar factores importantes alrededor del problema y de la posible solución.
- Postular una tesis (proponer un modelo) usando el conocimiento del fenómeno y estableciendo supuestos y limitaciones.
- Realizar experimentos apropiados y recolectar los datos asociados.
- Validar o rechazar la tesis planteada (validar o rechazar el modelo planteado).
- Establecer conclusiones y recomendaciones, así como posiblemente proponer una nueva tesis (lo que llevaría a un nuevo paso 3. en adelante).
Los modelos son de dos tipos: deterministas y aleatorios, dependiendo de si tienen o no componentes aleatorias.
4.3 ¿Modelo?
¿Qué es modelar?
Modelar consiste en elaborar una representación de un fenómeno o sistema con el propósito de describirlo, comprenderlo o predecir su comportamiento.
El proceso de modelado se inicia con la formulación de supuestos o hipótesis que simplifican la realidad y permiten concentrar el análisis en los aspectos más relevantes del problema. Estos supuestos son indispensables para que el problema resulte tratable y, a partir de ello, obtener conclusiones significativas.
Advertencia: La validez de las conclusiones depende de manera crítica de los supuestos planteados. Supuestos inadecuados, poco realistas o mal justificados pueden llevar a interpretaciones erróneas y a predicciones inválidas, incluso si el modelo aparenta ajustarse correctamente a los datos experimentales disponibles.
4.3.1 ¿Modelos?
Supongamos que una docente está interesada en “modelar” la posible relación entre el número de horas por semana de trabajo autónomo que dedican los estudiantes a resolver ejercicios prácticos (variable X) y el número total de problemas resueltos en el cuaderno del estudiante (variable Y).
Supongamos que al graficar los datos correspondientes a siete estudiantes, obtenemos lo siguiente:
Ahora, si quisiéramos ajustar un modelo que nos permita entender el comportamiento de los datos, podríamos ajustar una recta:
4.3.2 ¿Funciones?
El concepto general de función, se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto.
Las funciones son relaciones entre los elementos de dos conjuntos.
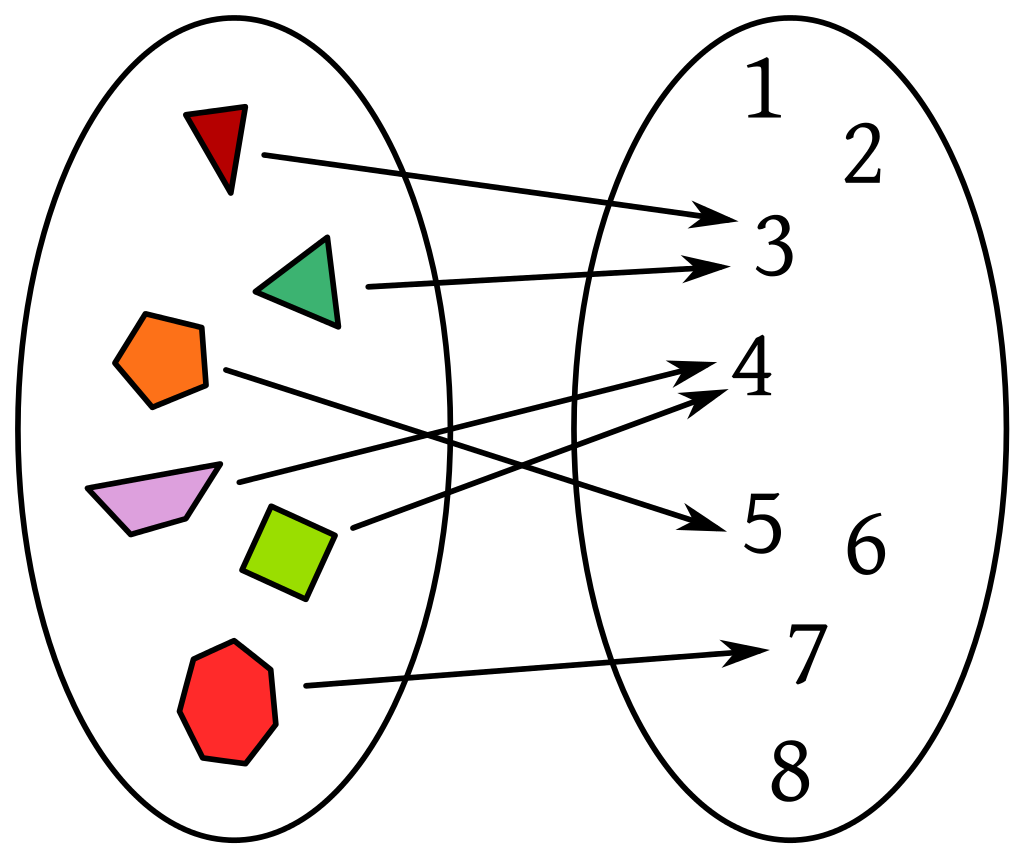
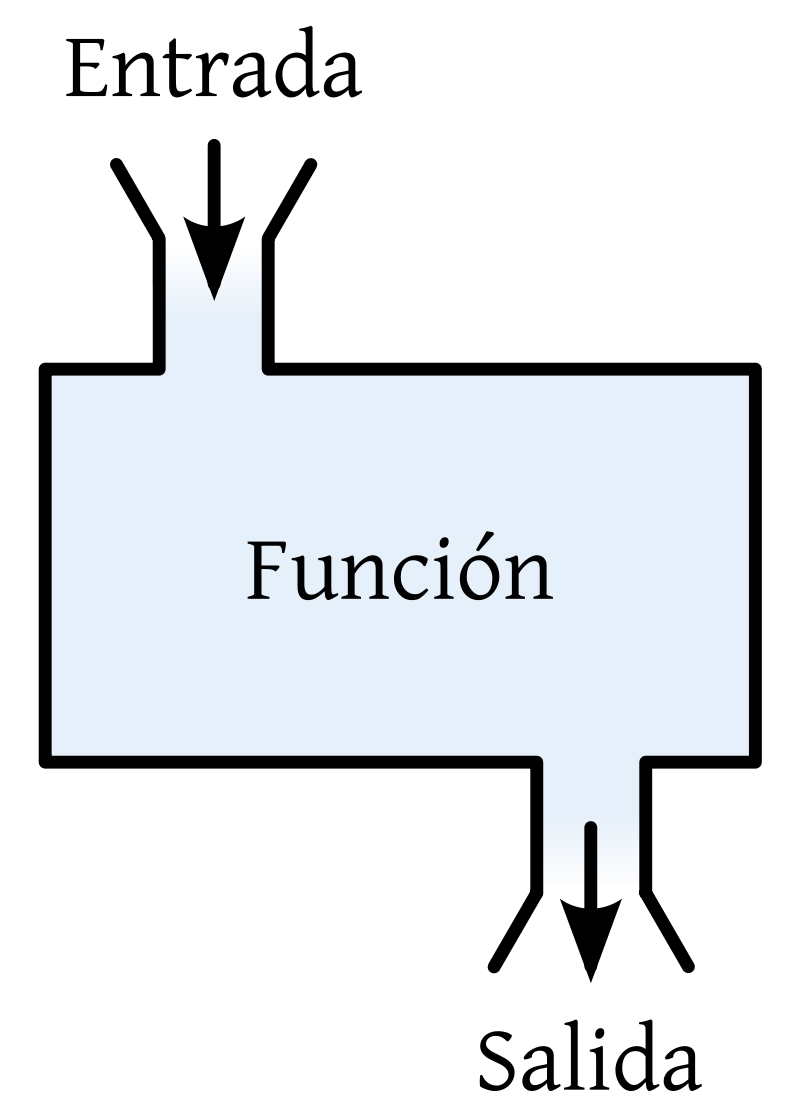
Una función también se puede ver como una “caja negra”, en donde para cosa que entra, obtenemos una a la salida (dada por la relación entre los elementos del conjunto de entrada y los del conjunto de salida).
4.3.3 ¿Función lineal?
Supongamos que estás planeando pintar una habitación de 100 metros cuadrados y necesitas calcular cuánto costará la pintura. Sabes que un litro de pintura cubre 20 metros cuadrados y cuesta $60 mil pesos.
Puedes calcular,
\textit{Costo por cada metro cuadrado}=\frac{\textit{Costo de un litro de pintura}}{\textit{Metros cuadrados que cubre}} = \text{\$} 3
\textit{Costo pintar la habitación de 100 metros} = ( 3 ) \times ( 100 ) = \text{\$} 300
Para una habitación de x metros, la fórmula que relaciona los metros (x) con el costo (y) sería y = f(x) = 3x. Esto quiere decir que el modelo sería lineal: y = f(x) = \beta_0 + \beta_1 x = (0) + (3)(x) = 3x. Los “betas” son los parámetros del modelo, que para la situación descrita toman los valores 0 y 3, respectivamente.
4.3.4 ¿Función cuadrática?
Imagina que lanzas una pelota hacia arriba desde el suelo con una velocidad inicial de 20 metros por segundo. Quieres saber cuán alto llegará la pelota o cuánto tiempo estará en el aire.
La ecuación que describe la altura de la pelota en cualquier momento después de lanzarla (la relación entre la posición vertical con respecto al tiempo), es:
\begin{aligned} h(x) &= h_0 + v_{0}x - \frac{1}{2}gx^2 \\ h(x) &= 0 + (20)(x) - \left(\frac{9.8}{2}\right) (x^2) \end{aligned}
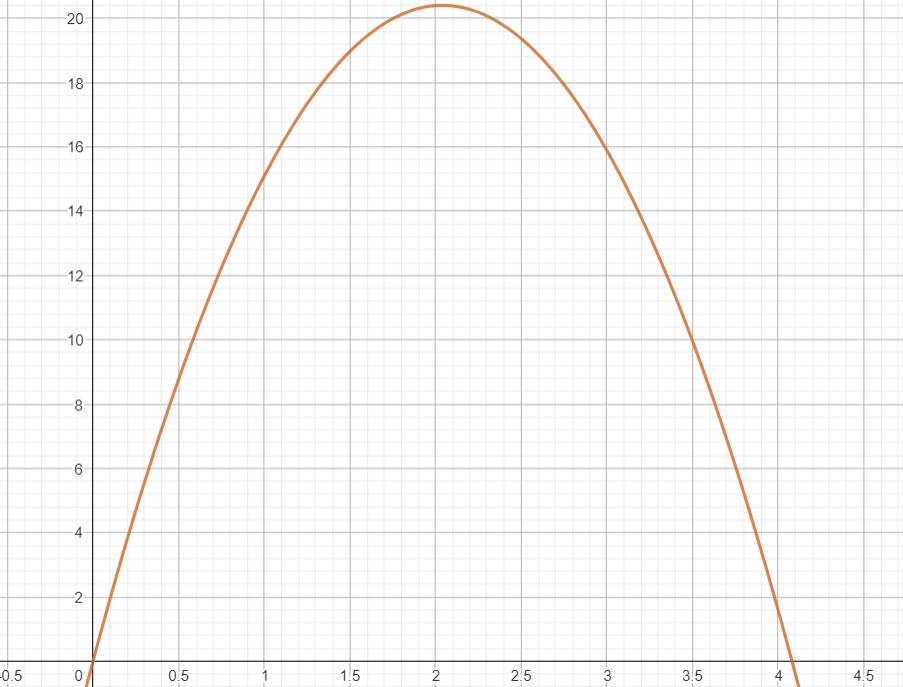
El modelo sería cuadrático: y = f(x) = \beta_0 + \beta_1 x + \beta_2 x^2.
4.3.5 ¿Función exponencial?
Tienes una sistema de seguridad con contraseña. El sistema permite hacer varios intentos, pero cada vez que intentas una contraseña y fallas, el tiempo que debes esperar para intentar nuevamente se duplica.
Por ejemplo, si la primera vez que fallas tienes que esperar 2 minutos, la segunda vez tendrás que esperar 4 minutos, la tercera vez 8 minutos, y así sucesivamente.
Si y representa el tiempo que debes esperar luego del x-ésimo intento fallido:
y =2^{x}
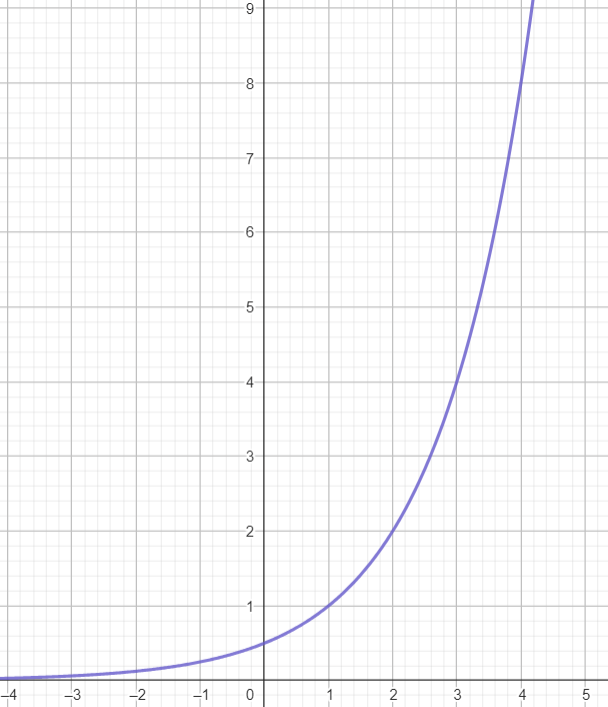
El modelo sería exponencial: y = f(x) = a^{\beta_0 + \beta_1 x}
4.3.6 ¿Función logarítmica?
Si haces más de 30 intentos, la caja fuerte se bloqueará para siempre. Ya lo has intentado tantas veces que no sabes cuantos intentos llevas, lo que si sabes es la cantidad de tiempo que tuviste que esperar en el más reciente intento.
Si quieres saber cuál intento fue, basándote en ese tiempo que tuviste que esperar, entonces:
\begin{aligned} y &= f(x) = 2^{x} \\ \log_2(y) &= f^{-1}(y) = x \end{aligned}
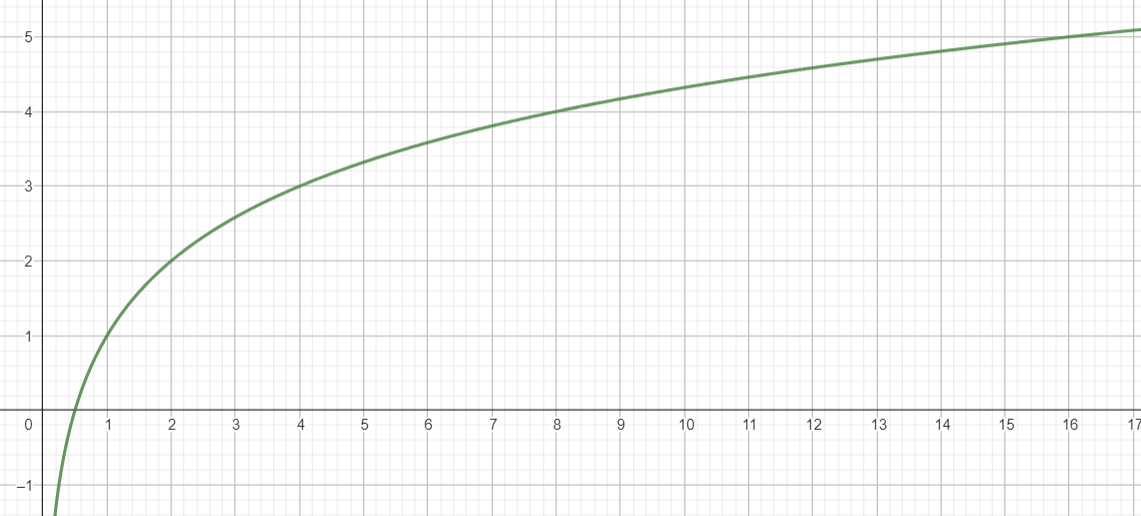
4.3.7 ¿Algunas funciones?
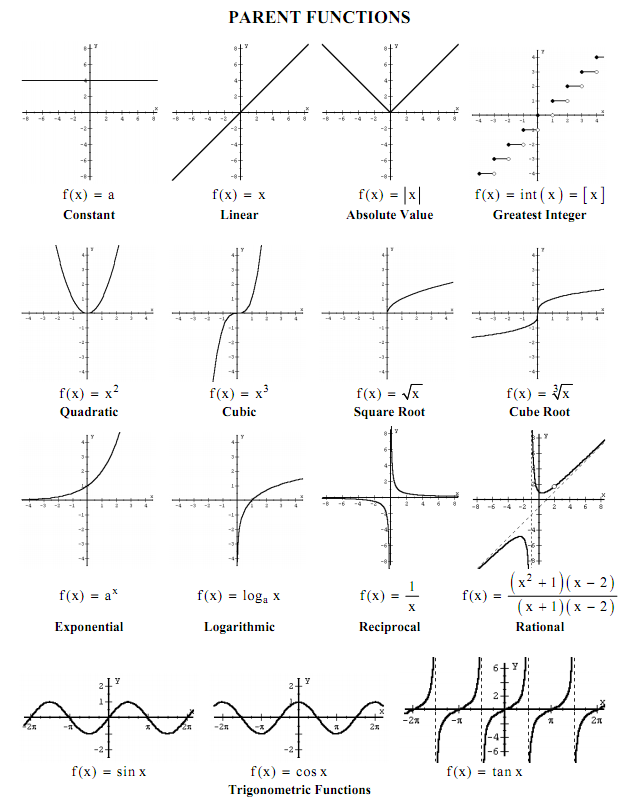
4.3.8 ¿Modelar?
Entonces en nuestro caso, modelar es encontrar, mediante alguna técnica o metodología, una relación funcional entre variables. Por ejemplo, la relación funcional entre una variable de interés, respuesta, dependiente o target, y una o más variables explicativas, predictoras, independientes o features.
4.3.9 ¿Ejemplo “trivial” determinista?
Ya dijimos que en este caso el modelo adecuado sería uno lineal: y = f(x) = \beta_0 + \beta_1 x, es decir, la recta que pasa por los puntos. ¿Cuáles deberían ser los valores para los parámetros (para los “betas”) del modelo que me relaciona las dos variables en esta situación (cuáles de todos los valores posibles asociados a todas las rectas posibles serían los que le corresponderían a la recta roja)?
4.3.10 ¿Ejemplo no determinista?
Por ejemplo, veamos lo que encontraremos al ir a donde nos lleva el siguiente enlace:
https://www.rossmanchance.com/applets/2021/regshuffle/regshuffle.htm
Recordemos que la ecuación de la recta que relaciona a una variable x con una variable y se escribe así:
y = f(x) = \beta_0 + \beta_1 x
en donde \beta_0 representa el intercepto y \beta_1 representa la pendiente de la recta.
Entonces, queremos encontrar valores, para los parámetros \beta_0 y \beta_1, tales que minimicen la suma de los errores (distancias entre lo observado y lo daría usando el modelo) al cuadrado: \begin{aligned} g(\beta_0,\beta_1) &= e^2_1 + e^2_2 + \dots \\ &= \big(y_1 - f(x_1)\big)^2 + \big(y_2 - f(x_2)\big)^2 + \dots \\ &= \big(y_1 - \left(\beta_0 + \beta_1 x_1\right)\big)^2 + \big(y_2 - \left(\beta_0 + \beta_1 x_2\right)\big)^2 + \dots \\ \end{aligned}
Este problema de encontrar los valores que minimizan (problema de optimización) se puede resolver usando lo que llamamos derivadas.
4.4 ¿Derivadas?
Derivadas (Universo Mecánico 3) (Ciencias TV - Mar 14, 2021 - 27:22)
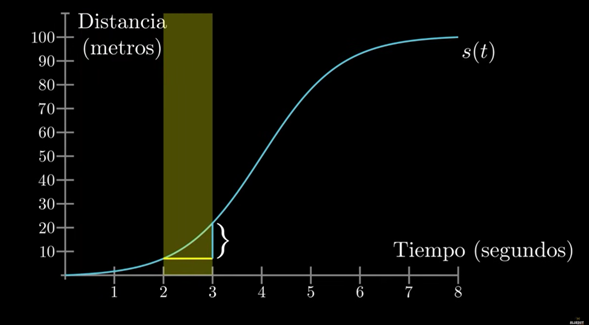
Supongamos que tenemos un carro que está en reposo, luego se empieza a mover incrementando gradualmente su rapidez, en algún punto, el auto empezará a disminuir su velocidad hasta que se haya detenido del todo.
Podemos ver que en los primeros segundos, la distancia recorrida es muy corta, cuando acelera, esta distancia se hace más grande, hasta que, al empezarse a detener, esta distancia se hace corta nuevamente. ¿Cómo podemos hallar la rapidez de este carro en un instante?
4.4.1 ¿Tasa o razón de cambio en un instante?
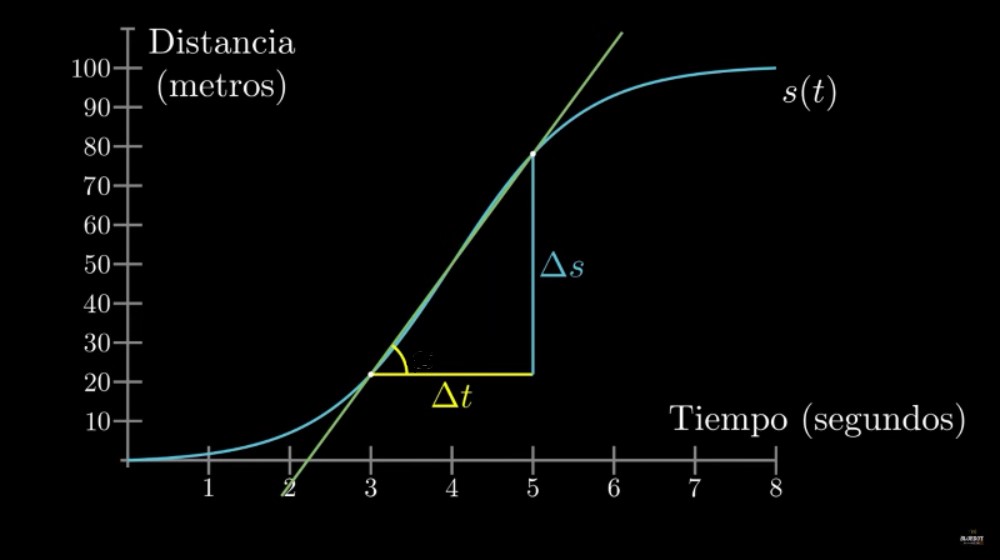
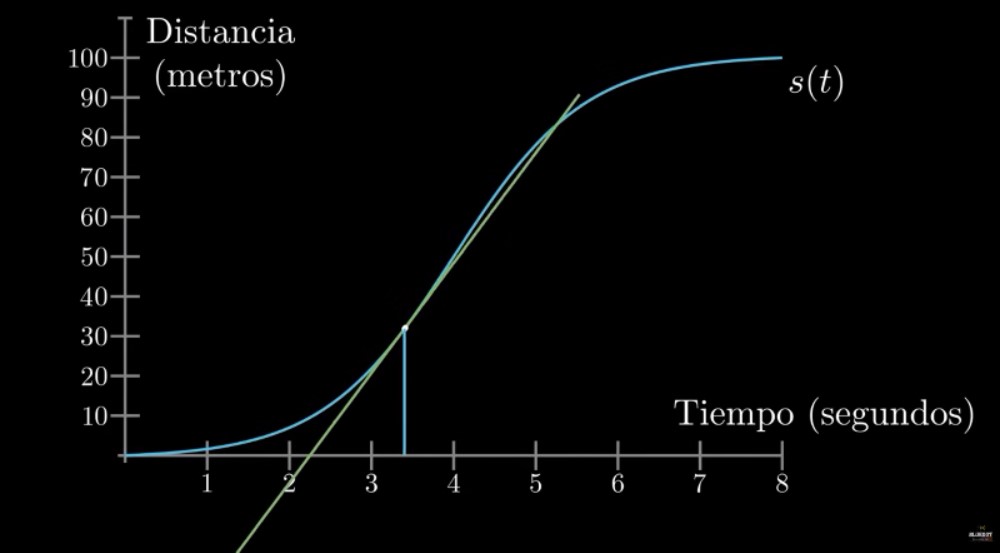
4.4.2 Derivada como…
Pendiente de la recta tangente
Aproximación lineal
4.4.3 ¿Derivación?
\begin{aligned} \frac{d}{d\beta} g(\beta) &= g'(\beta) \\ \end{aligned}
En el caso de g(\beta) = \beta^n, se tiene que g'(\beta) = n \beta^{n-1}, \begin{aligned} \frac{d}{d\beta} \beta^n &= n \beta^{n-1} \end{aligned}
En Internet se pueden encontrar tablas con las derivadas de muchas funciones básicas (por ejemplo en https://es.wikipedia.org/wiki/Anexo:Derivadas), y calculadoras de derivadas, en donde uno da la función y la herramienta le devuelve la derivada de la función (por ejemplo en https://www.derivative-calculator.net/).
4.5 ¿Optimización?
Supongamos que tienes una fábrica que produce un producto determinado. Quieres minimizar los costos de producción para maximizar tus ganancias. Los costos pueden estar relacionados con varios factores, como el costo de las materias primas, la mano de obra, la energía, entre otros. Puedes tener una función que represente el costo total de producción en función de la cantidad de producto fabricado. Esta función podría ser, por ejemplo, una combinación de costos fijos y costos variables.
¿Cómo encuentro el valor de \beta para el cual la función y = g(\beta) alcanza un mínimo (o un máximo)?
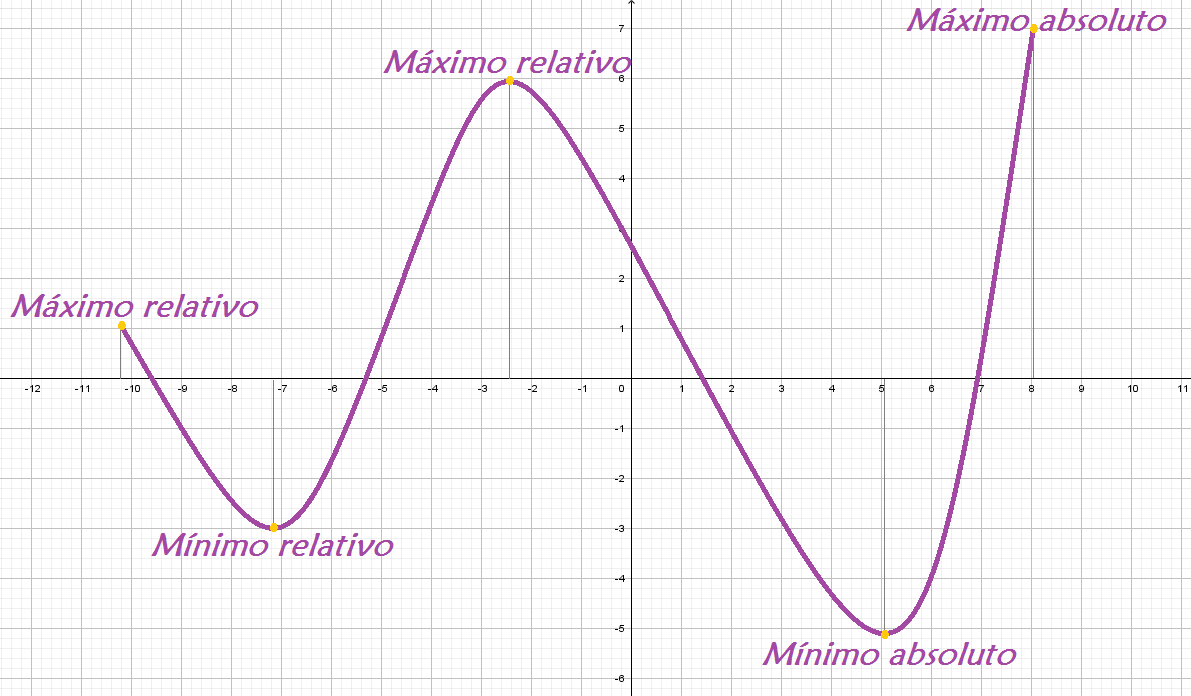
4.5.1 ¿Máximos y mínimos?
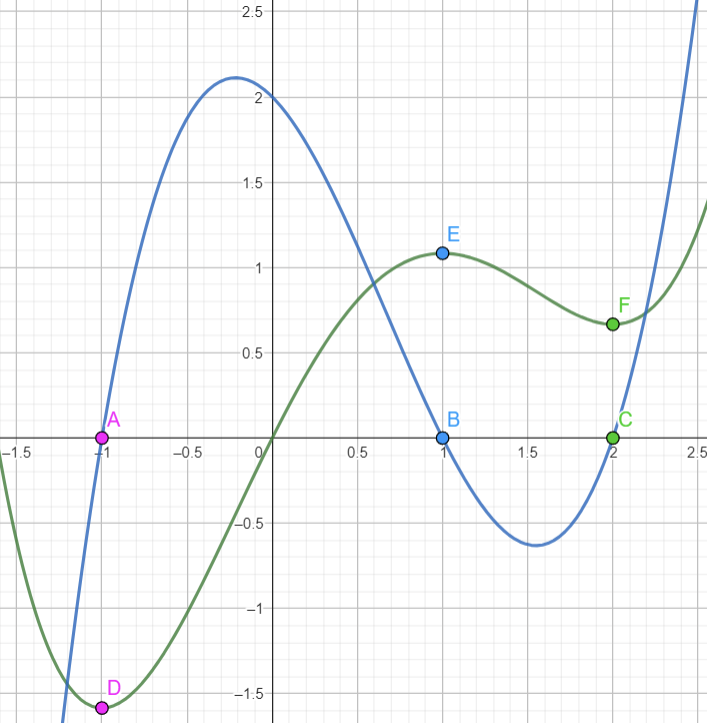
Supongamos que la gráfica en verde representa a la función g(\beta), entonces la gráfica azul corresponde a la derivada g'(\beta).
¿Qué tienen en común los valores de \beta que hacen que la función del gráfico en verde alcance un máximo o un mínimo (sin importar si es local o global)?
4.5.2 ¿Para qué todo lo anterior?
Recordemos que queremos encontrar valores para \beta_0 y \beta_1 tales que minimicen la suma de los errores (distancias entre lo observado y lo daría usando el modelo) al cuadrado: \begin{aligned} g(\beta_0,\beta_1) &= e^2_1 + e^2_2 + \dots = \big(y_1 - f(x_1)\big)^2 + \big(y_2 - f(x_2)\big)^2 + \dots \\ &= \big(y_1 - \left(\beta_0 + \beta_1 x_1\right)\big)^2 + \big(y_2 - \left(\beta_0 + \beta_1 x_2\right)\big)^2 + \dots \\ \end{aligned}
Usando derivadas, igualando a cero y encontrando la solución para la ecuaciones resultantes, se obtiene que: \begin{aligned} \beta_1 &= \rho \frac{\sigma_y}{\sigma_x} = b \\ \beta_0 & = \mu_y - b \mu_x = a \end{aligned}
https://www.rossmanchance.com/applets/2021/regshuffle/regshuffle.htm
Otro ejemplo:
McGivern Jewelers se ubica en Levis Square Mall, justo al sur de Toledo, Ohio. Recién publicó un anuncio en el periódico local en el que indicaba la forma, el tamaño, el precio y el grado de corte de 33 de sus diamantes en existencia.
Lind, Marchal & Wathen (2012). Estadistica Aplicada a los Negocios y la Economia. (15a. ed.) McGraw-Hill. Capítulo 4, Ejercicio 37.
En la siguiente hoja de cálculo (Google Sheets) encontrarán los datos asociados a las cuatro variables de los 33 diamantes, los cuales se encuentran en la pestaña “Datos” de la hoja de cálculo (Google Sheets): EjemploDatosDiamantesLind(15Ed)4.37.gsheet
En la siguiente hoja de cálculo (Google Sheets) encontrarán un ejemplo relacionado con varios cálculos paso a paso, incluyendo el del intercepto y la pendiente de la recta que mejor ajusta para precio y tamaño de los diamantes: EjemploCalculosMedidasDescriptivasDosVariablesContinuas.gsheet
4.6 ¿Área bajo la curva?
Integración (Universo Mecánico 7) (Ciencias TV - Apr 11, 2021 - 27:23)
Vamos en el carro nuevamente, nos vamos a mover en línea recta con una rapidez constante de v(t) = 10 m/s ¿Que distancia recorremos en t = 8s?
La distancia recorrida por el auto será igual al área bajo la gráfica de la función v(t), que para este caso es el área de un rectángulo.
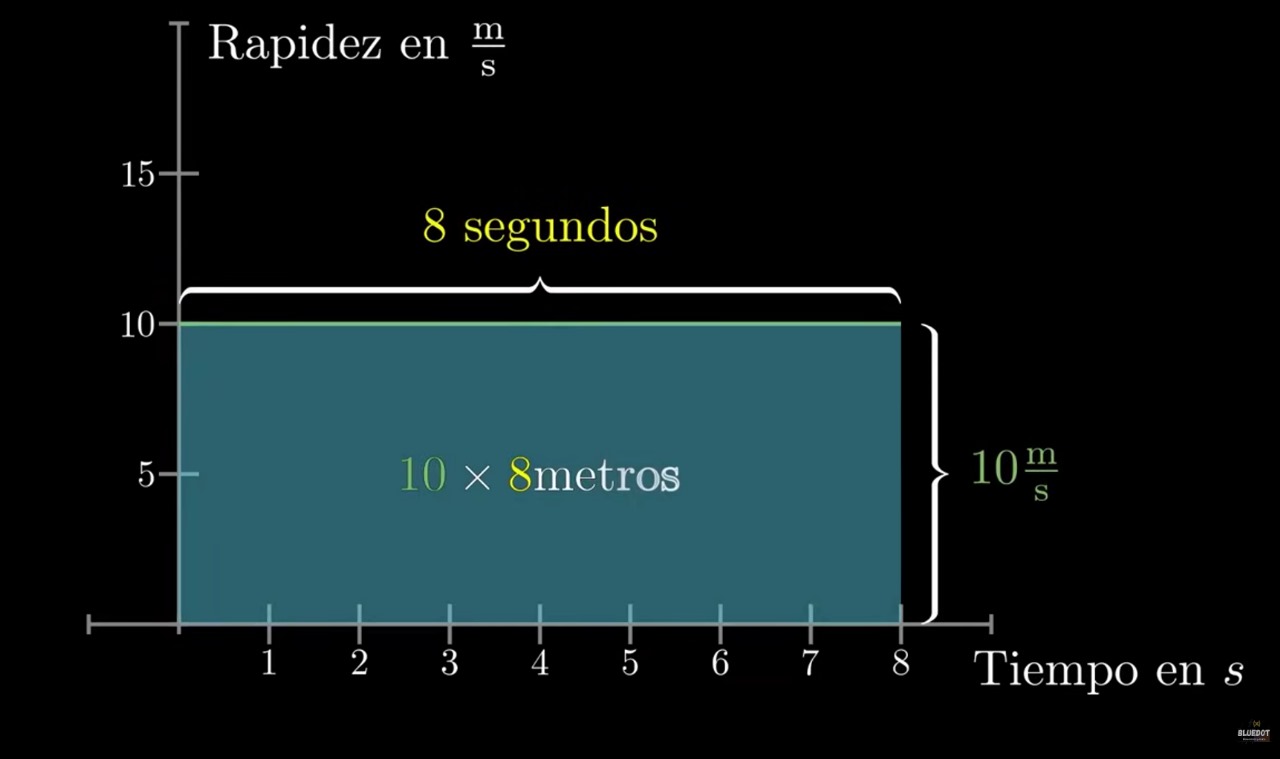
¿Pero qué pasaría si v(t) no es una constante?
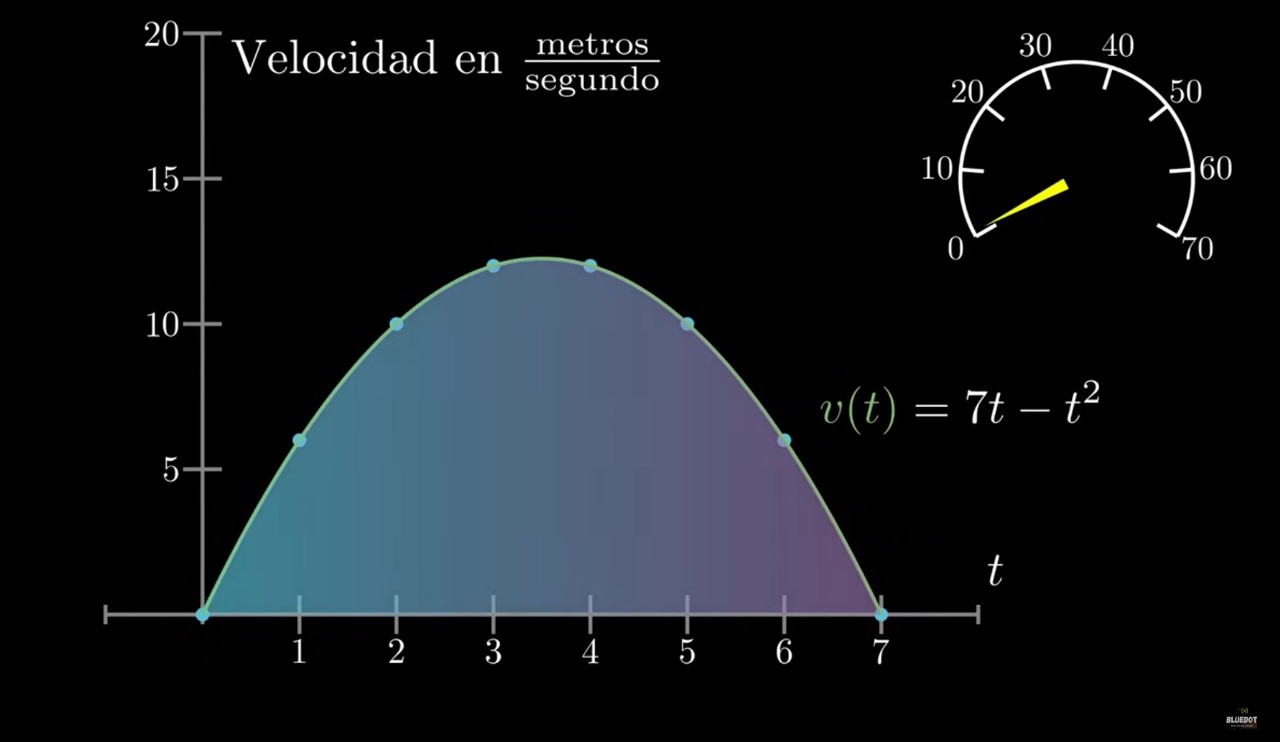
¿Cómo encontramos el área bajo la curva para cualquier función?
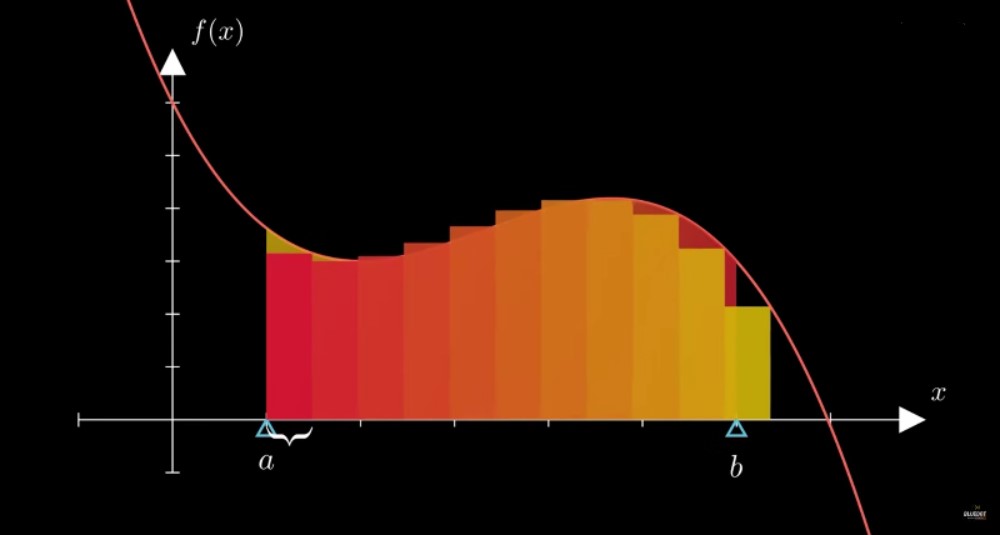
4.6.1 ¿Suma de rectángulos?
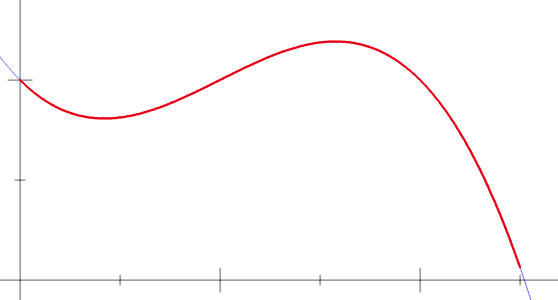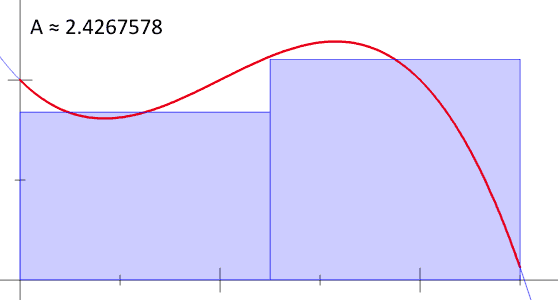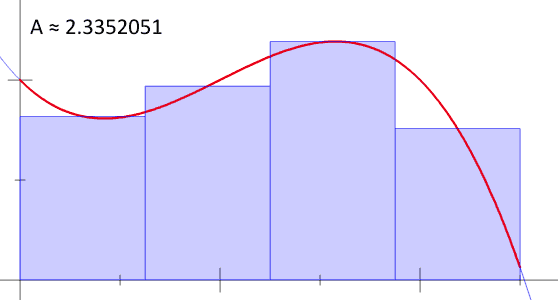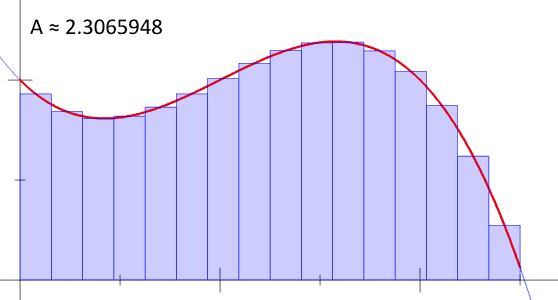
El área bajo la curva sería aproximadamente la suma de las áreas de los rectángulos de base cada vez más pequeña. A = A_1 + A_2 + \dots
4.6.2 ¿Notación?
El área bajo la curva de la función f(x), entre a y b a lo largo del eje x, se denota en símbolos matemáticos como: A = \int_a^b f(x) \, dx donde el símbolo \int representa la letra ‘S’ de la palabra latina “Summa”.
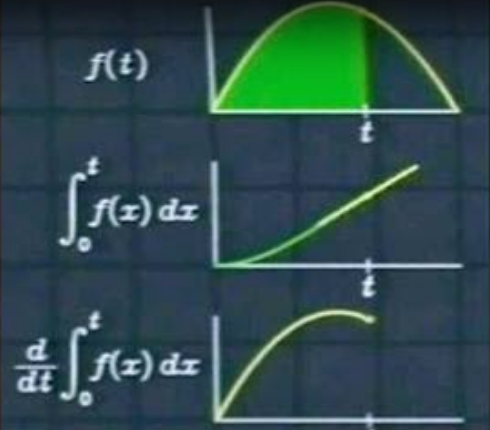
4.6.3 ¿Relación con derivar?
Si A(x) = \int_{a}^{x} f(t) \, dt entonces resulta que, A'(x) = f(x) Lo que quiere decir que el proceso de encontrar el área bajo la curva (integrar) es el proceso inverso de derivar, de manera análoga a como sumar es el proceso inverso de restar.
4.6.4 ¿Integración?
Si sabemos que, \begin{aligned} F'(x) &= f(x) \\ \end{aligned} entonces calcular el área bajo la curva es fácil, \int_{a}^{b} f(t) \, dt = \text{Area} = F(b) - F(a)
En Internet se pueden encontrar tablas con las integrales de muchas funciones básicas (por ejemplo en https://es.wikipedia.org/wiki/Anexo:Integrales), y calculadoras de integrales, en donde uno da la función y la herramienta le devuelve la integral de la función (por ejemplo en https://www.integral-calculator.com/).
4.6.5 ¿Para qué el area bajo la curva?
Imaginemos una curva suave que representa teóricamente la manera en que se distribuyen los resultados posibles de una variable, por ejemplo: los puntajes de un examen de admisión.
El área bajo la curva entre 60 y 80 indicaría la probabilidad (teórica) de que los individuos de mi población (¿países?, ¿personas?) tengan una expectativa de vida entre los 60 y los 80 años.