2 Fund. computacionales
Fundamentos computacionales y de programación
Para esta sección se han tomado algunos elementos de las siguientes fuentes:
- Joyanes Aguilar, L. (2020). Fundamentos de programación: algoritmos, estructura de datos y objetos (5th ed.). McGraw Hill.
- Fundamentos de programación, con implementaciones en Python y R: orientados a las bases de la computación científica, requerida en estadística, ciencia de datos y otros https://cjtorresj.quarto.pub/ple/
2.1 ¿Fundamentos computacionales?
Los fundamentos computacionales son esenciales en la ciencia de datos, el aprendizaje automático y la inteligencia artificial.
- Métodos y modelos en estas áreas requieren un soporte computacional eficiente para ser implementados y escalados.
- Además, usualmente requieren trabajar con conjuntos de datos reales, los cuales suelen ser voluminosos y de alta dimensión, lo que aumenta la exigencia computacional.
2.1.1 ¿Aspectos clave?
El procesamiento y manejo de datos es fundamental y requiere bases computacionales sólidas para su aplicación.
- Todo análisis comienza con la manipulación y el preprocesamiento de datos.
- Esto incluye operaciones de limpieza, transformación y estructuración.
- Estas tareas aseguran que los datos estén en un formato adecuado para el análisis.
- También permiten que los modelos produzcan resultados confiables.
- La implementación de todo lo anterior depende del uso efectivo y eficiente de herramientas, lenguajes y recursos computacionales.
- Lo cual a su vez, demanda unos fundamentos computacionales sólidos y desarrollar habilidades en dicho uso.
- Todo análisis comienza con la manipulación y el preprocesamiento de datos.
La reproducibilidad y la automatización también son fundamentales.
- La reproducibilidad permite repetir un análisis bajo similares condiciones.
- Este es un requisito clave en investigación y aplicaciones prácticas.
- Para lograrlo se requiere una implementación computacional cuidadosa y estandarizada.
- Por otra parte, automatizar permite manejar tareas repetitivas o recurrentes.
- Ambas prácticas exigen habilidades de programación y comprensión de sistemas computacionales.
- La reproducibilidad permite repetir un análisis bajo similares condiciones.
La escalabilidad y optimización de los cálculos es otro aspecto central.
- Los algoritmos suelen requerir cálculos complejos y repetitivos.
- Estos cálculos deben ejecutarse de forma eficiente para optimizar tiempo y recursos.
- Comprender los fundamentos computacionales permite, entre otros, optimizar procesos y aplicar modelos en grandes volúmenes de datos sin perder precisión.
- Estas operaciones demandan una infraestructura adecuada (hardware, software, etc.) para que sean viables en la práctica.
- Los algoritmos suelen requerir cálculos complejos y repetitivos.
El conocimiento de las herramientas y lenguajes de programación adecuados resulta indispensable para implementar técnicas y modelos de ciencia de datos, aprendizaje automático e inteligencia artificial.
- El uso de lenguajes computacionales, como R y Python, se vuelve indispensable.
- Ambos cuentan con librerías robustas y optimizadas para el análisis y el modelado de datos.
- Estas librerías o paquetes permiten enfocarse en el desarrollo de modelos y el análisis, sin necesidad de programar desde cero los algoritmos subyacentes.
- De esta manera se facilita el trabajo, aumentando la eficiencia y la productividad.
- El uso de lenguajes computacionales, como R y Python, se vuelve indispensable.
2.1.2 ¿Por qué y para qué es necesario aprender lo computacional?
- Abre puertas a una amplia gama de oportunidades laborales, en un mercado con alta demanda de personas con dichas habilidades.
- Ofrece una ventaja competitiva y permite desarrollar proyectos personales y profesionales.
- En ciencia de datos, facilita el manejo, procesamiento y análisis de grandes volúmenes de información.
- Brinda herramientas y flexibilidad para trabajar de manera eficiente y escalable.
- Permite la creación, personalización y mejora de modelos y algoritmos para obtener mejores resultados.
- Hace posible la automatización de flujos de trabajo, optimizando tiempo y recursos.
- Las habilidades que se tengan en este ámbito se potencian y su impacto se amplifica gracias a la existencia y el uso de herramientas de inteligencia artificial.
2.2 ¿Computación y computadores?
- 1642: Blas Pascal. Primera calculadora mecánica. Sumas y restas.
- 1694: Gottfried Leibniz. Sumar, restar, multiplicar y dividir.
- 1819: Joseph JacQuard. Bases de las tarjetas perforadas.
- 1835: Charles Babbage. Máquina analítica: calculadora que incluía un dispositivo de entrada, dispositivo de almacenamiento de memoria, una unidad de control y dispositivos de salida.
- 1841: Ada Augusta, condesa de Lovelace. Publica los trabajos de Babbage. Primera programadora.
- 1884: Herman Hollerith. Inventó máquina calculadora que funcionaba con electricidad y tarjetas perforadas. 1896. Creó la empresa Tabulating Machine Company (IBM en 1924).
- 1940s: Colossus Mark I: “the world’s first electronic digital programmable computer”. ABC: “the first automatic electronic digital computer”. ENIAC: “the first electronic programmable computer built in the U.S.”.
2.2.1 ¿“Universal computing machine” o “universal Turing machine”?
¿Qué es una máquina de Turing? (Derivando - Jan 10, 2018 - 5:17)
Turing, A. M. (1937). On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society. 2. 42 (1): 230–265.
De Castro Korgi, Rodrigo (2004). Teoría de la computación : lenguajes, autómatas, gramáticas. [online] Bogotá, Colombia: Universidad Nacional de Colombia. https://repositorio.unal.edu.co/handle/unal/53477

2.2.2 ¿Modelo von Newmann?
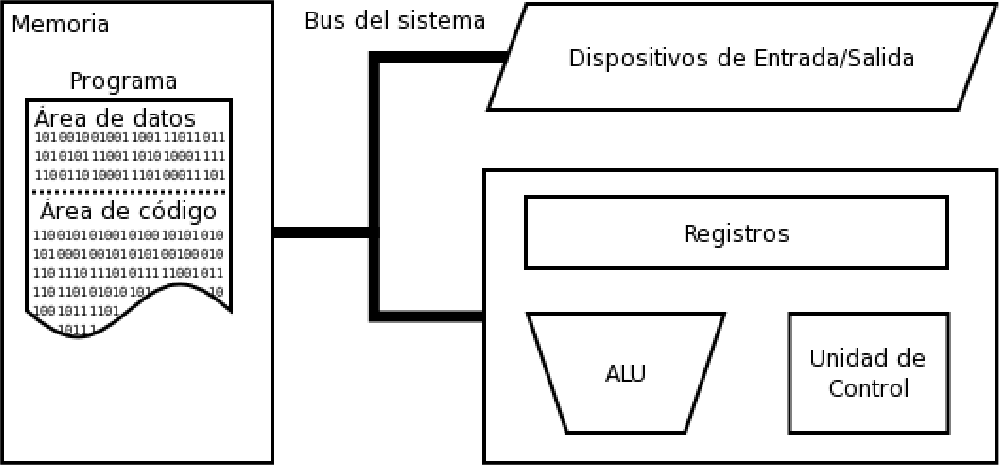
2.2.3 ¿Organización de un computador?
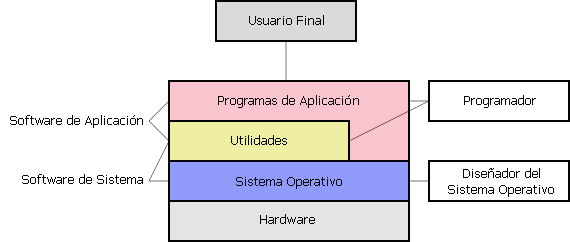
2.2.4 ¿El idioma del computador?
bit = binary digit (dígito binario). Se almacena un cero (0) o un uno (1), apagado o encendido. 8 bits = 1 byte.
ASCII (American Standard Code for Information Interchange) o US-ASCII : 128 caráteres.
| Caracter | Código ASCII | Binario |
|---|---|---|
| \vdots | \vdots | \vdots |
| A | 65 | 01000001 |
| B | 66 | 01000010 |
| C | 67 | 01000011 |
| \vdots | \vdots | \vdots |
Unicode: 143859 caráteres (Versión 13.0. Marzo 2020). UTF-8 (Unicode Transformation Formats): Codificación que en el 2020 era usada por más del 95% de los sitios web.
2.3 ¿Lenguajes de programación?
2.3.1 ¿La programación de computadores?
“Un programa de computador es un conjunto detallado de instrucciones paso a paso que indican al dispositivo las acciones a realizar con exactitud. Si cambiamos el programa, entonces la computadora realiza una secuencia diferente de acciones y, por consiguiente, ejecutará una tarea diferente”.
Un programa de computador suele ser la implementación de un algoritmo, en algún lenguaje de programación, que podrá ser ejecutado en un computador.
“El software (los programas) regulan el hardware (la parte física)”. “El proceso de creación de software se llama programación”.
2.3.2 ¿Qué es un lenguaje de programación?
Un lenguaje de programación es un lenguaje artificial con reglas gramaticales precisas que permite expresar instrucciones para controlar el comportamiento el comportamiento lógico o físico de un sistema informático.
- Un conjunto de instrucciones escritas en un lenguaje de programación constituye un programa informático.
- Sirve como puente entre el programador y el computador, cuyo lenguaje nativo es el binario (ceros y unos).
- Cada lenguaje posee una sintaxis (forma de escribir) y una semántica (significado).
- Conocer el paradigma y el lenguaje en que está escrito un programa es indispensable para modificarlo o mejorarlo, e incluso para usarlo adecuadamente.
Importante: los lenguajes de marcado (como HTML, LaTeX o Markdown) no son lenguajes de programación. Su objetivo es organizar y dar formato al contenido, no ejecutar instrucciones lógicas ni cálculos.
2.3.3 ¿Tipos de lenguajes de programación?
Lenguajes de máquina: instrucciones en cadenas binarias.
Lenguajes de bajo nivel: cercanos al hardware, como el ensamblador.
Lenguajes de medio nivel: combinan acceso al hardware con cierta abstracción.
Lenguajes de alto nivel: más cercanos al lenguaje natural, fáciles de usar y entender.
Existen múltiples lenguajes, cada uno con sus ventajas y desventajas según el contexto de uso.
- Existen numerosos lenguajes de programación (por ejemplo, ver los que se listan y comparan en https://en.wikipedia.org/wiki/Comparison_of_programming_languages).
- Aquí se hace una comparación bajo ciertos criterios específicos: https://julialang.org/benchmarks/
2.3.4 ¿Traducción de los lenguajes?
Un computador solo entiende instrucciones en cadenas binarias, por lo que todo programa escrito en algún lenguaje de programación debe traducirse a lenguaje de máquina.
Se requiere un mecanismo de traducción / programa traductor que convierta las instrucciones del lenguaje elegido en instrucciones ejecutables por el computador, y que además, ponga en evidencia en dónde no estamos siguiendo la sintaxis o las reglas del lenguaje.
La traducción puede realizarse principalmente de dos formas, compilación o interpretación.
2.3.4.1 ¿Compilación?
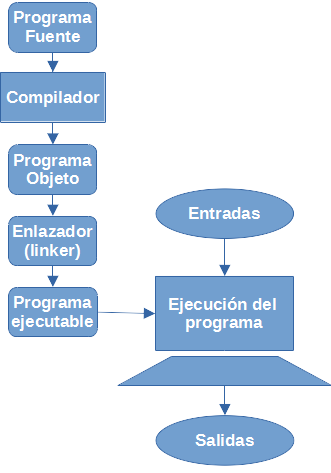
2.3.4.2 ¿Interpretación?
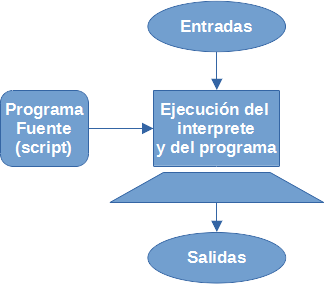
2.3.5 ¿Paradigmas de programación?
- Un paradigma de programación es un enfoque que define cómo se diseñan e implementan soluciones computacionales a un problema.
- Cada paradigma se distingue por la manera en que abstrae los elementos del problema y por los métodos utilizados para resolverlo.
Leer: Programming paradigm https://en.wikipedia.org/wiki/Programming_paradigm
La programación imperativa es un paradigma de programación que utiliza sentencias para cambiar el estado de un programa. De manera similar a la forma imperativa en los lenguajes naturales, la programación imperativa consiste en comandos que la computadora debe ejecutar. Este paradigma se centra en describir cómo opera el programa paso a paso, en lugar de enfocarse en una descripción de alto nivel de los resultados esperados.
La programación estructurada es un paradigma de programación que busca mejorar la claridad, la calidad y el tiempo de desarrollo de un programa mediante el uso extensivo de estructuras de control de selección y repetición.
La programación procedimental es un paradigma de programación basado en el concepto de llamada a procedimientos. Los procedimientos (un tipo de rutina o subrutina) contienen una serie de pasos computacionales “en bloque”, que pueden ser llamados en cualquier punto de la ejecución de un programa, incluso desde otros procedimientos o desde sí mismo.
La programación orientada a arreglos se refiere a soluciones que permiten aplicar operaciones a un conjunto completo de valores a la vez. Los lenguajes de programación modernos que soportan la programación orientada a arreglos (también conocida como programación vectorial o de múltiples dimensiones) están diseñados específicamente para generalizar operaciones en escalares de modo que puedan aplicarse de manera transparente a vectores, matrices y arreglos de dimensiones superiores. En estos lenguajes, una operación que actúa sobre arreglos completos se conoce como una operación vectorizada.
La programación orientada a objetos es un paradigma de programación basado en el concepto de objetos, los cuales pueden contener datos y código: los datos en forma de campos (también llamados atributos o propiedades) y el código en forma de procedimientos (también conocidos como métodos).
La programación funcional es un paradigma de programación en el cual los programas se construyen aplicando y componiendo funciones. Es un paradigma declarativo en el que las definiciones de las funciones son árboles de expresiones que mapean valores a otros valores, en lugar de ser una secuencia de sentencias imperativas que actualizan el estado en ejecución del programa.
2.3.6 ¿Paradigmas y lenguajes de programación?.
Los lenguajes de programación pueden incorporar varios paradigmas (lenguajes multiparadigma). En el siguiente enlace podrán encontrar una rápida revisión de la relación entre algunos lenguajes de programación y algunos paradigmas asociados a dichos lenguajes:
https://en.wikipedia.org/wiki/Comparison_of_multi-paradigm_programming_languages
2.4 ¿Algoritmos y la resolución de problemas?
En matemáticas, lógica, ciencias de la computación y disciplinas afines, un algoritmo es un conjunto de instrucciones o reglas que son:
- Definidas y no ambiguas
- Ordenadas
- Finitas
Un algoritmo permite resolver un problema, realizar un cómputo, procesar datos o llevar a cabo diversas tareas “de manera automática”.
2.4.1 ¿Medios de expresión?
- Máquina de Turing: Modelo matemático diseñado por Alan Turing que formaliza o es equivalente al concepto de algoritmo.
- Diagrama de flujo: Representación gráfica de un algoritmo mediante símbolos conectados con flechas que muestran la secuencia de pasos o instrucciones.
- Pseudocódigo: Descripción estructurada que combina elementos del lenguaje natural y de los lenguajes de programación.
- Descripción de “alto nivel”: Planteamiento verbal del problema y explicación en detalle del funcionamiento paso a paso del algoritmo.
2.4.1.1 ¿Diagrama de flujo?
La representación de un algoritmo mediante un diagrama de flujo utiliza unos símbolos estándar. Los principales símbolos son:
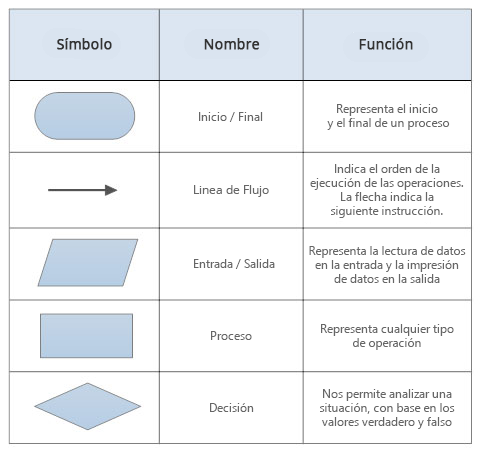
2.4.1.2 ¿Pseudocódigo?
Esta representación es muy similar a la que se empleará en la escritura al programar.
//comentario_1
const
nombre_de_constante_1 <- valor_1
…
var
tipo_de_dato_1: nombre_de_var_1, nombre_de_var_2, …
…
inicio
acción_1
acción_2
…
//Algunas acciones podrían ser de escritura:
escribir(expresión_cadena)
//Algunas acciones podrían ser de lectura:
leer(variable)
//Algunas acciones podrían ser de asignación:
nombre_de_variable <- expresión
…
fin
2.4.2 ¿Elementos básicos iniciales de un algoritmo?
Datos: la información que el algoritmo recibe, procesa o genera.
- Tipos de dato básico atómico (no compuesto):
- Entero (int)
- Real (float)
- Lógico (booleano)
- Carácter (char)
- Entero (int)
- Variables: espacios de memoria donde se almacenan valores que pueden cambiar durante la ejecución.
- Tipos de dato básico atómico (no compuesto):
Identificadores: nombres que se asignan a variables u otros elementos para poder utilizarlas dentro del algoritmo.
Palabras clave o reservadas: términos con un significado específico y fijo en la formulación de algoritmos, que por ende no se pueden usar para nombres de variables.
Operaciones: acciones que permiten transformar o manipular los datos.
- Asignación: dar un valor a una variable.
- Aritméticas: suma, resta, multiplicación, división, etc.
- Lógicas: comparaciones y condiciones.
- Asignación: dar un valor a una variable.
Expresiones: combinaciones de datos y operaciones que producen un resultado.
Comentarios: anotaciones que describen el propósito o funcionamiento de ciertas partes del algoritmo, sin afectar su ejecución.
Ejemplo 2.1 Algoritmo que calcule e imprima el área de un triangulo a partir de la base y la altura dadas por el usuario
- En diagrama de flujo (Flowgorithm):
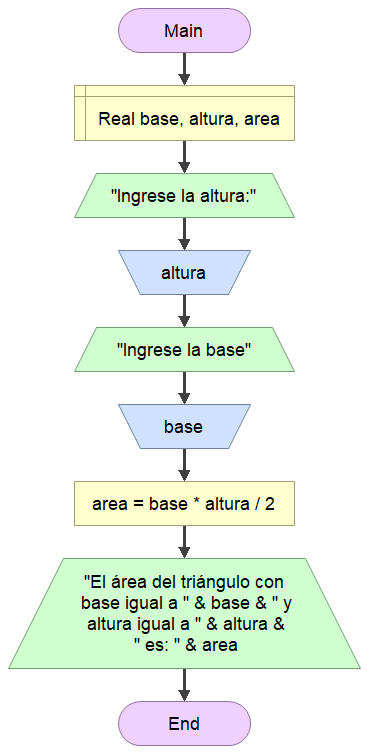
- En pseudocódigo:
//El usuario ingresa dos números reales asociados a
//la altura y la base de un triángulo y el algoritmo
//devuelve el valor asociado al área del triángulo
var
real: base, altura, area
inicio
escribir(“Ingrese la altura”)
leer(altura)
escribir(“Ingrese la base”)
leer(base)
area <- base * altura / 2
escribir(“El área del triángulo es:”)
escribir(area)
fin
2.5 ¿Programación estructurada?
La programación estructurada surgió como una respuesta a los problemas de la programación en sus inicios, donde el código “espagueti” (lleno de saltos goto) era la norma.
La programación estructurada es un paradigma de programación que se basa en la idea de que cualquier programa puede crearse utilizando únicamente tres tipos de estructuras de control:
Secuencia: Ejecutar instrucciones una después de otra, en orden.
Selección (o Condición): Tomar decisiones (ejecutar un bloque de código u otro) basadas en una condición.
Repetición (o Iteración): Repetir un bloque de código mientras se cumpla una condición.
Además, todas las estructuras se pueden incluir unas dentro de otras cuando el algoritmo así lo requiera.
En 1966, los científicos Corrado Böhm y Giuseppe Jacopini demostraron matemáticamente que cualquier algoritmo / programa computable, sin importar su complejidad, puede escribirse usando solo las tres estructuras básicas (secuencia, selección e repetición). Este teorema es la base teórica de la programación estructurada.
2.5.1 ¿Control del flujo de un programa?
El flujo de un programa define el orden en que se ejecutan las instrucciones.
- Por defecto, sigue la estructura secuencial: las sentencias se ejecutan una tras otra en el orden en que aparecen (como en el ejemplo del área de un triángulo).
- Cuando es necesario modificar ese flujo se utilizan:
- Estructuras de selección: permiten decidir qué sentencias ejecutar según una condición.
- Estructuras de repetición: permiten ejecutar un conjunto de sentencias varias veces de manera controlada (también se les llama: estructuras iterativas, bucles, ciclos, loops).
- Estructuras de selección: permiten decidir qué sentencias ejecutar según una condición.
2.5.1.1 ¿Estructura secuencial?
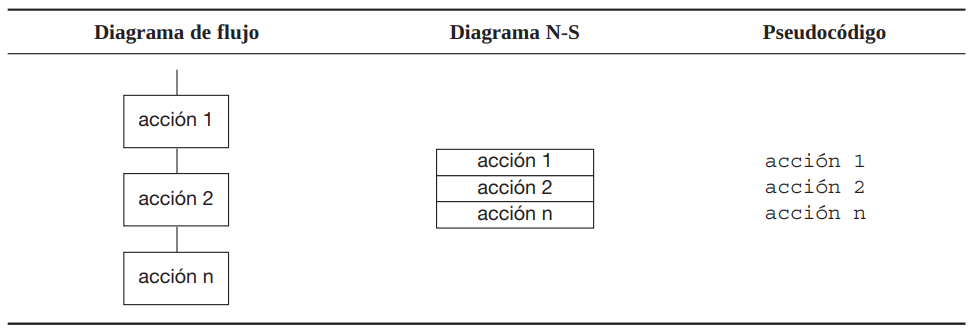
2.5.1.2 ¿Estructura de selección?
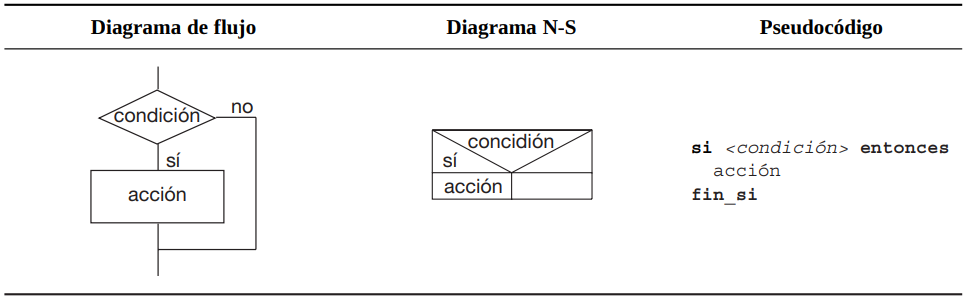
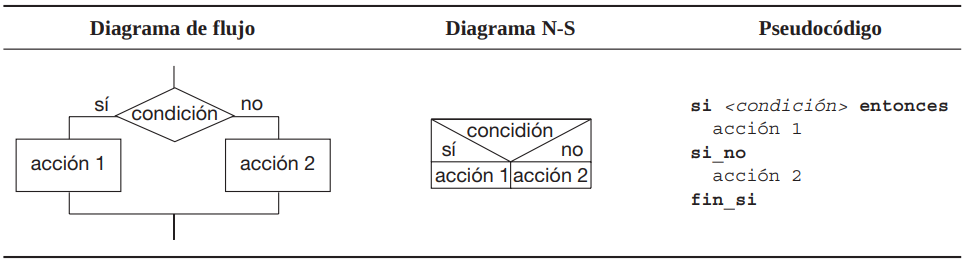
2.5.1.3 ¿Estructura de repetición?
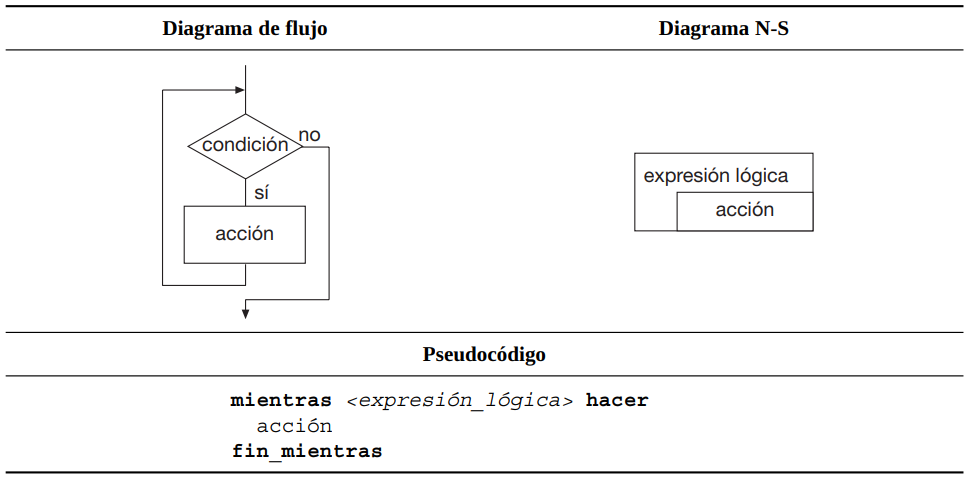
Ejemplo 2.2 Algoritmo que determine y diga si un número dado, entero mayor que uno (>1), es primo o no lo es.
En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1. Por el contrario, los números compuestos son aquellos que tienen algún divisor natural aparte de sí mismos y del 1, y, por lo tanto, pueden factorizarse.
Los números primos son importantes porque constituyen la base de toda la aritmética. Esto se debe al teorema fundamental de la aritmética, que establece que cualquier número entero mayor que 1 se puede descomponer de manera única como producto de primos. Por eso se les llama los “átomos de los números”: sin ellos, no existiría una estructura básica para organizar la aritmética.
- En criptografía moderna son esenciales porque muchos sistemas de seguridad digital, como RSA, dependen de la dificultad de factorizar números grandes en primos. Esa asimetría hace posible la seguridad en contraseñas y transacciones.
- En algoritmos y computación, los primos permiten construir métodos eficientes de búsqueda, encriptación y compresión. Ejemplo: tablas hash y generadores de números pseudoaleatorios que usan primos para distribuir datos uniformemente.
- En teoría de la información y telecomunicaciones, sus propiedades permiten modular señales y reducir errores en la transmisión de datos, aplicándose en la teoría de códigos y en tecnologías de espectro ensanchado.
- En la naturaleza, aparecen en patrones evolutivos. Ejemplo: las cigarras periódicas emergen cada 13 o 17 años (ambos primos) para evitar sincronizarse con depredadores.
- En biología molecular y genética, se aplican en algoritmos de búsqueda de secuencias de ADN, optimizando el reconocimiento de patrones.
En síntesis: los números primos no son simples curiosidades matemáticas, sino la base de la aritmética y un recurso esencial para la seguridad digital, la computación, la transmisión de información y la explicación de fenómenos naturales y biológicos.
Para diseñar el algoritmo debo tener en cuenta: ¿qué sé de los números primos? ¿Qué propiedades de ellos, o de los que no son números primos, puedo aprovechar para decidir rápidamente si un número dado es primo o no? Sin embargo, no olvide que el trabajo no lo va a hacer usted, debe ser el computador el que lo haga por sí mismo, mecánicamente, y sin intervención suya.
Supongamos que lo primero que se me ocurre es poner al computador a verificar todos los números como posibles divisores. Esto funciona, pero puede que sea ineficiente. ¿qué sería mejor, verificar divisores yendo del mayor al menor número o al revés? ¿en realidad se necesita hacer tantas verificaciones o se pueden hacer menos? ¿cuántas verificaciones se harían, por ejemplo para el número 1234567891?
En una segunda versión, pienso que no es necesario revisar posibles divisores para un número divisible por 2, es decir, un número par. El único primo par es 2. Además, si un número no es divisible por 2, entonces ya no será divisible por ningún otro número par. Esto quiere decir que no se necesitaban tantas verificaciones como se había pensado inicialmente. ¿cuántas verificaciones se harían en este caso?
En una tercera versión, noto que se puede ser aún más eficiente: no es necesario probar con todos los números, sino solo hasta aquel cuya multiplicación consigo mismo supere al número dado (¿por qué?). ¿cuántas verificaciones se harían con esta versión?
Diagrama de flujo:
Archivo con diagrama de flujo en Flowgorithm
Pseudocódigo:
var
entero: k, i
booleano: seguirBusc
cadena: textoRes
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo determina si un número entero mayor que uno es primo o no lo es”)
escribir(“Por favor, ingrese un número entero mayor que uno”)
leer(k)
mientras k < 2 hacer
escribir(“Por favor, ingrese un número entero MAYOR QUE UNO”)
leer(k)
fin_mientras
//Se usará ” ” para los que son primos y ” NO ” para los que no
textoRes <- ” ”
si k > 3 entonces
si k % 2 == 0 entonces
escribir(“2 SI es divisor de” & k)
textoRes <- ” NO ”
si_no
escribir(“2 NO es divisor de” & k)
i <- 3
seguirBusc <- true
mientras seguirBusc hacer
si k % i == 0 entonces
escribir(i & ” SI es divisor de ” & k)
textoRes <- ” NO ”
seguirBusc <- false
si_no
escribir(i & ” NO es divisor de ” & k)
i <- i + 2
si i * i > k entonces
seguirBusc <- false
fin_si
fin_si
fin_mientras
fin_si
fin_si
escribir(“El número” & k & textoRes & “ES PRIMO”)
fin
Ejemplo 2.3 Algoritmo que obtenga e imprima una aproximación de la raíz cuadrada de un número real no negativo dado
La tabla babilónica YBC 7289 (c. 2000-1650 a. C.) proporciona una aproximación de \sqrt{2} en cuatro dígitos sexagesimales (sistema numérico que usaban los babilonios, base 60), que sería correcto con cinco (5) cifras decimales (sistema numérico que usamos nosotros, base 10).

El primer algoritmo explícito para aproximar raíces cuadradas es conocido como método de Herón, en honor al matemático griego Herón de Alejandría, quien lo publicó alrededor del año 60 d. C. en su obra Métrica. Este método también es denominado método babilónico, aunque no existe evidencia directa de que realmente fuera conocido y aplicado por los babilonios (solamente existen conjeturas informadas).
Diagrama de flujo:
Archivo con diagrama de flujo en Flowgorithm
Pseudocódigo:
var
entero: n
real: c, cMedios, a, aNew, eps
inicio
escribir(“Bienvenido”)
escribir(“Este algoritmo obtiene una aproximación de la raíz cuadrada de un número real no negativo dado (c). El algoritmo se detendrá cuando el cambio de una aproximación a la siguiente sea inferior a un número real positivo cercano a cero (epsilon)”)
escribir(“Por favor, ingrese un número real no negativo (c)”)
leer(c)
si c == 0 o c == 1 entonces
escribir(“La raíz cuadrada de” & c & ” es igual a ” & c)
si_no
escribir(“Por favor, ingrese un numero real positivo cercano a cero (epsilon)”)
leer(eps)
cMedios <- c / 2
n <- 2
a <- 0.5 + cMedios //Este es a_1
aNew <- 0.5 * a + cMedios / a
mientras a – aNew > eps hacer
n <- n + 1
a <- aNew
aNew <- 0.5 * a + cMedios / a
fin_mientras
escribir(“La raíz cuadrada de” & c & ” es aproximadamente igual a ” & aNew)
escribir(“(con el epsilon dado igual a” & eps & “, la aproximación corresponde al término” & n & ” de la sucesión)“)
fin_si
fin
2.6 ¿Programación procedimental?
La programación procedimental es una manera de ampliar el paradigma de programación imperativa estructurada.
Es aplicable tanto en lenguajes de bajo nivel como en lenguajes de alto nivel.
La resolución de problemas complejos se facilita si se dividen en subproblemas:
- La solución de esos subproblemas se puede realizar mediante subalgoritmos.
- cada subalgoritmo está diseñado para realizar una tarea específica, y dependiendo de si devuelven datos o no, se suelen denominar funciones o procedimientos.
Teniendo lo anterior en cuenta la programación procedimental consiste en:
- Englobar una serie de instrucciones dentro de un procedimiento o función.
- Llamar a dicho procedimiento o función cada vez que se requiera.
2.6.1 ¿Diseño descendente y programación modular?
El diseño descendente consiste en descomponer un problema en otros más pequeños y sencillos.
La programación modular resuelve de manera independiente esos subproblemas:
- Esta técnica amplía y completa el diseño descendente como método de resolución de problemas.
- Permite proteger la estructura de la información asociada a cada subproblema.
En este enfoque:
Existe un algoritmo principal o conductor que transfiere el control a los subalgoritmos.
Cada subalgoritmo, al terminar su tarea, devuelve el control al algoritmo que lo llamó:
- Los subalgoritmos son de menor tamaño y dificultad que el principal.
- Deben seguir las reglas de la programación estructurada.
- Se representan con las herramientas habituales de programación.
- Los subalgoritmos son de menor tamaño y dificultad que el principal.
El empleo de la programación modular facilita notablemente el diseño de programas.
Ventajas principales:
- Permite que varios programadores trabajen simultáneamente en distintas partes de un algoritmo, ya que los módulos serían independientes.
- Se puede modificar un módulo sin afectar a los demás.
- Cada subalgoritmo se escribe una sola vez, aunque se necesite en distintas partes de un algoritmo o en varios algoritmos distintos.
2.6.2 ¿Subalgoritmos / Subprogramas?
2.6.2.1 ¿Funciones?
Una función toma uno o más valores, denominados argumentos o parámetros y, según el valor de éstos y las acciones de la función, al final devuelve un resultado a nombre de la función.
La definición de una función expresada en pseudocódigo tendría la siguiente forma:
inicio_función
…
acciones
…
devolver(expresión)
fin_función
Para invocar a una función se utiliza su nombre seguido por los parámetros entre paréntesis.
La llamada a una función se podrá colocar en cualquier instrucción en donde se pueda usar una expresión.
2.6.2.2 ¿Procedimientos?
La declaración de un procedimiento es similar a la de una función. Las pequeñas diferencias son debidas a que el nombre del procedimiento no se encuentra asociado a ningún valor o resultado.
La definición de un procedimiento expresada en pseudocódigo tendría la siguiente forma:
inicio_procedimiento
…
acciones
…
fin_procedimiento
Un procedimiento se invoca o se llama de la misma manera que una función, pero al no devolver un valor o resultado, un procedimiento solamente se puede usar como instrucción del algoritmo principal y no como parte de una expresión.
2.6.3 ¿Recursión?
La recursión es una forma de resolver problemas en la que una idea o proceso se define a partir de sí mismo. En programación, esto significa que una función o procedimiento puede llamarse a sí mismo para resolver un problema.
Aunque en los computadores normalmente usamos repeticiones llamadas iteraciones (bucles), la recursión resulta especialmente útil cuando trabajamos con problemas que se repiten en sí mismos.
Ideas clave para entender la recursión:
- Debe existir una condición de salida: es decir, una regla clara que indique cuándo detenerse.
- Cada paso debe acercarse a esa condición de salida: si no avanzamos hacia la meta, el proceso nunca termina.
- Cada llamada recursiva usa nuevos valores: la función no se queda con los datos anteriores, sino que trabaja con los datos de la nueva llamada.
- La memoria del computador guarda cada llamada apilándolas: la última llamada en entrar es la primera en resolverse (como cuando apilamos platos y sacamos primero el que quedó arriba).
Para tener en cuenta:
- Todo algoritmo recursivo se puede convertir en uno iterativo (con bucles).
- A veces la versión recursiva es más sencilla de entender, sobre todo cuando el problema tiene una estructura que “se repite en sí misma”.
- Sin embargo, la versión iterativa suele estar más cerca de un funcionamiento imperativo secuencial, lo cual tiene a ahorrar tiempo y memoria.
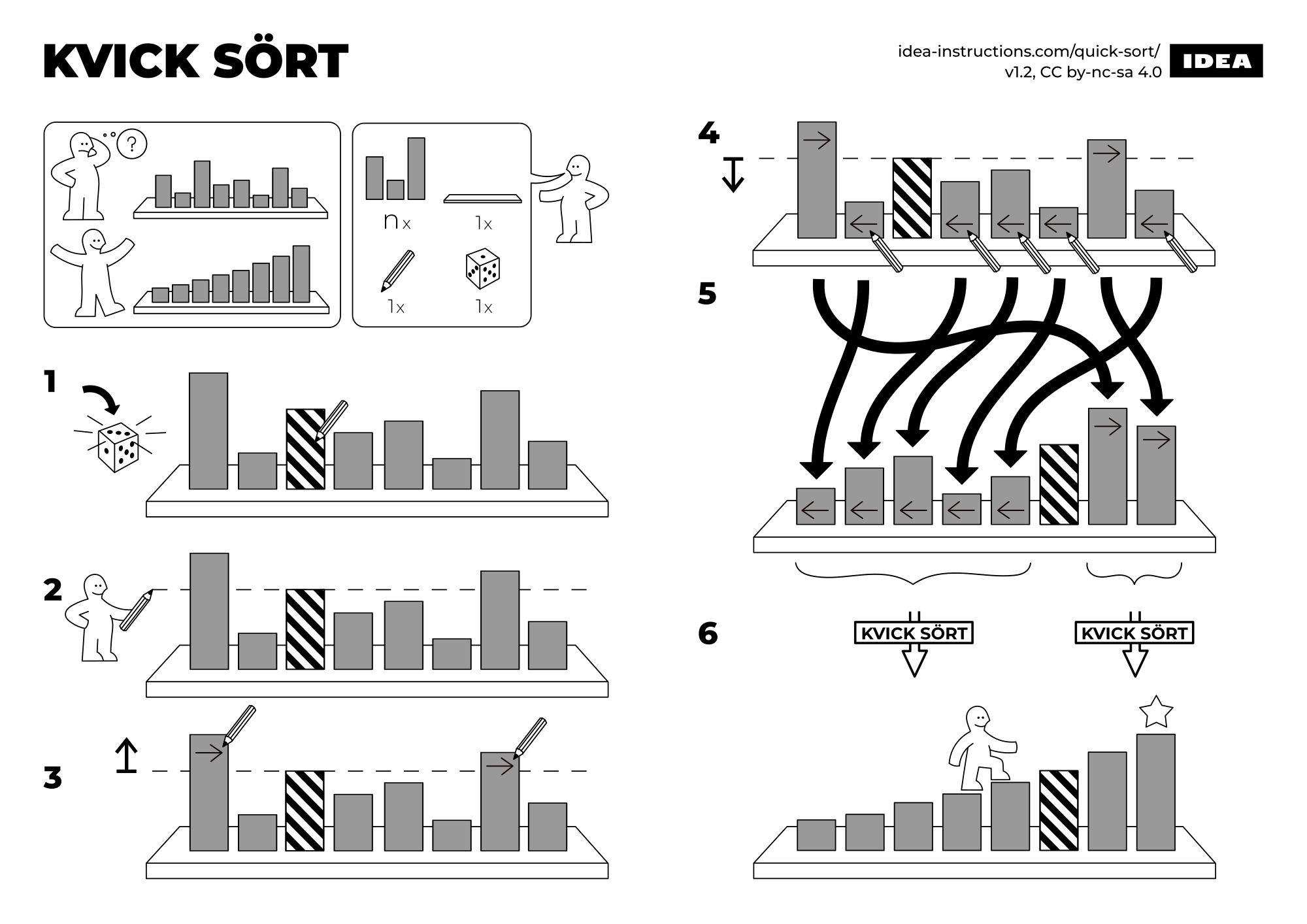
2.6.4 ¿Ámbito de las variables?
Cuando hablamos de variables en programación nos referimos a “cajas” donde guardamos información (un número, un texto, un valor lógico, etc.).
Ahora bien, esas cajas no siempre están disponibles en todo el programa: depende de dónde las declaremos. A esto se le llama ámbito de la variable.
Una variable global es la que está disponible en todo el programa. Si la declaramos en el algoritmo principal, cualquier parte del programa puede acceder a ella.
Una variable local es la que solo existe dentro de un subalgoritmo (por ejemplo, dentro de una función o un procedimiento). En este caso, la variable solo puede usarse en ese lugar y no afecta ni se mezcla con las del programa principal.
Es importante entender que dos variables con el mismo nombre pueden existir al mismo tiempo: una en el programa principal y otra en un subalgoritmo. Aunque se llamen igual, son distintas y no interfieren entre sí.
Trabajar de esta manera tiene una gran ventaja: cada subalgoritmo se vuelve independiente, lo que facilita dividir un problema en partes más pequeñas sin que unas se confundan con otras.
Esto es lo que se conoce como independencia modular, y permite diseñar programas más claros, organizados y fáciles de mantener.
Sin embargo, en algunos lenguajes de programación, puede que se ofrezca algún mecanismo particular para que una parte del programa “salga de su espacio” y altere valores externos.
Esta capacidad tiene dos caras:
- Ventaja: un subprograma puede influir directamente en el estado general del programa sin necesidad de devolver valores.
- Riesgo: se pierde claridad, porque ya no es fácil saber qué parte del programa está cambiando cada variable. Por ello, la recomendación más común es tratar de no usar estos mecanismos particulares, y de esa manera, conservar la independencia modular, evitar confusiones, facilitar la revisión del programa y el trabajo en equipo.
2.6.5 ¿Paso de parámetros por valor?
Paso por valor o paso por copia significa que cuando se llama un subprograma, este recibe una copia de los valores de los parámetros en un espacio de memoria aparte.
Si el valor de un parámetro se modifica mediante una o más asignaciones o instrucciones del subprograma, el cambio solamente tiene efecto dentro del subprograma y no por fuera de él.
En varios lenguajes de programación, los parámetros que sean de un tipo de dato primitivo o elemental se suelen pasan por valor / copia.
2.6.6 ¿Paso de parámetros por referencia?
En este caso, el subprograma no recibe una copia sino una “referencia” de donde se encuentran los datos originales, lo que hace al subprograma trabajar directamente con ellos y no con una copia.
Esto sirve principalmente para evitar duplicar información, ya que entre más datos se tengan que copiar, más tiempo y memoria se invertirá en hacer y almacenar las copias.
Este comportamiento es particularmente útil y se vuelve casi indispensable al trabajar con tipos de datos compuestos dado que una sola variable de este tipo podría estar almacenando muchos datos a la vez.
En varios lenguajes de programación, los parámetros que sean de tipo de dato arreglo (array) se suelen pasar por referencia / dirección. Esto teniendo en cuenta que una sola variable de tipo arreglo, o de otro tipo de dato compuesto, podría estarse encargando de almacenar muchos datos a la vez.
2.7 ¿Arreglos?
Previamente se han mencionado los tipos de datos primitivos o elementales (atomic types) que representan un único dato como un número entero o real, una letra o un valor booleano.
Sin embargo, en muchas situaciones se requiere trabajar con una colección de valores que agrupados hacen parte de un todo.
Los tipos de datos compuestos son estructuras de datos que permiten en una misma variable e identificador tener más de un dato o valor primitivo.
Ahora haremos una revisión del tipo de dato arreglo o array, tipo de dato compuesto y estructura de datos básica que incorporan una gran mayoría de lenguajes de programación.
Un arreglo es una colección finita de datos del mismo tipo, que se almacenan en posiciones consecutivas de memoria y reciben un nombre común.
Para referirse a un determinado elemento de un arreglo se deberá utilizar un índice, el cual especifica su posición relativa dentro del arreglo.
Los arreglos podrán ser unidimensionales o multidimensionales. Sin embargo, como la memoria de la computadora es básicamente lineal, un arreglo multidimensional en realidad se tendrá que almacenar en memoria como un arreglo unidimensional equivalente, pero con mecanismos que me permiten “navegarlo” fácilmente bajo el concepto multidimensional que tengo de él.
2.7.1 ¿Arreglos unidimensionales?
En el caso de un arreglo unidimensional estamos hablando de una estructura de datos que tendría cierta equivalencia o similaridad con el objeto matemático: vector, ya que ambos corresponden a una secuencia de valores ordenados, que son indexados por un único índice asociado a una única dimensión.
El tamaño de un arreglo unidimensional es la cantidad de elementos del arreglo en su única dimensión.
Las variables de tipo arreglo se deben declarar como cualquier otra variable.
Sin embargo, cuando un arreglo se declara, adicionalmente se debe informar el tipo de dato de los elementos del arreglo.
Es decir, la declaración se debe hacer en función de otro tipo de dato conocido o previamente definido.
En pseudocódigo, la declaración de un arreglo unidimensional podría hacerse de la siguiente manera:
arreglo tipo_dato: nombre_arreglo[tamaño_arreglo], …
…
Dependiendo del lenguaje de programación, la indexación de los elementos del arreglo: nombre_arreglo va de 0 a tamaño_arreglo - 1 o de 1 a tamaño_arreglo.
Usando los valores del índice, los elementos de un arreglo son igualmente accesibles y cualquiera de ellos puede ser seleccionado para lo que se desee hacer.
Para seleccionar el elemento en la posición i del arreglo, se escribe: nombre_arreglo[i].
Para todo efecto práctico, cada elemento del arreglo: nombre_arreglo se comporta como si fuese una variable de tipo: tipo_dato.
Los elementos de un arreglo se pueden recorrer por completo, mediante el uso de una estructura iterativa y una variable que pase por todos los valores de la indexación. Por ejemplo:
mientras i < tamaño_arreglo hacer
escribir(nombre_arreglo[i])
i <- i + 1
fin_mientras
De la misma manera en que ocurre con los demás tipos de datos, un subprograma puede recibir variables de tipo arreglo o puede devolver una variable de tipo arreglo.
La capacidad de devolver una variable de tipo arreglo permite a un subprograma devolver uno o más valores o datos de un mismo tipo de dato.
Especialmente en el caso de los arreglos, debemos tener claras las dos formas distintas en que un programa principal puede pasar y un subprograma puede recibir los parámetros, parámetros por valor (paso de una copia) y parámetros por referencia (paso de una dirección de memoria).
2.7.2 ¿Arreglos multidimensionales?
Los arreglos multidimensionales son aquellos en donde cada elemento del arreglo está indexado por más de un índice (por más de un subíndice cuando los elementos del arreglo se denotan de la siguiente manera: a_{i,j,k,l}).
La dimensión de un arreglo es la cantidad de índices distintos que tenga o use el arreglo para sus elementos (en a_{i,j,k,l} serían 4 dimensiones).
Cada índice tendrá una cantidad máxima de valores posibles y esa cantidad se denomina el tamaño de cada dimensión (n, m, o y p si 0 \leq i < n, 0 \leq j < m, 0 \leq k < o, 0 \leq l < p).
La cantidad total de elementos del arreglo es igual al producto de los tamaños de todas las dimensiones ((n)(m)(o)(p)).
Cuando se habla del tamaño de un arreglo, se está refiriendo a los tamaños de cada dimensión (el arreglo con elementos a_{i,j,k,l} es de tamaño n \times m \times o \times p).
En pseudocódigo, la declaración de un arreglo multidimensional podría hacerse de la siguiente manera:
arreglo tipo_dato: nombre_arreglo[tam_dim1, tam_dim2, tam_dim3, …], …
…
Obviamente, un arreglo bidimensional necesita dos índices para poder identificar a cada elemento del arreglo (de la misma manera en que cada elemento de una matriz tiene asociado dos subíndices).
La referencia a un determinado elemento del arreglo bidimensional requiere emplear un primer valor para el primer índice y un segundo valor para el segundo índice (si es de alguna utilidad, el primer valor se puede interpretar como un número de fila y el segundo como un número de columna, pero no se está obligado a seguir esta interpretación, el computador no interpreta solo hace).
Por ejemplo, nombre_arreglo[0, 0] hace referencia al elemento de la posición: 0, 0 (en la interpretación mencionada, el elemento de la fila 0 y la columna 0).
Cada elemento del arreglo tendrá todos los beneficios y limitaciones de una variable de tipo: tipo_dato.
Para seleccionar un elemento de un arreglo multidimensional bastaría hacer: nombre_arreglo[i, j, k, ...], para los valores i, j, k, etc. que correspondan a la posición del elemento deseado.
Para recorrer por completo los elementos de un arreglo bidimensional se requiere usar dos estructuras iterativas anidadas y dos variables que pasen por todos los valores de ambas indexaciones (una estructura y una variable por cada una de las dos dimensiones).
Por ejemplo, fijando el valor para el primer índice mientras se recorren los valores del segundo índice (recorrido por filas, es decir se fija una fila mientras se recorren las columnas, para luego pasar a la siguiente fila, etc.):
mientras i < tam_dim1 hacer
j <- 0
mientras j < tam_dim2 hacer
escribir(nombre_arreglo[i, j])
j <- j + 1
fin_mientras
i <- i + 1
fin_mientras
o, fijando el valor para el segundo índice mientras se recorren los valores del primer índice (recorrido por columnas, es decir se fija una columna mientras se recorren las filas, para luego pasar a la siguiente columna, etc.):
mientras j < tam_dim2 hacer
i <- 0
mientras i < tam_dim1 hacer
escribir(nombre_arreglo[i, j])
i <- i + 1
fin_mientras
j <- j + 1
fin_mientras
Para recorrer los elementos de un arreglo de d dimensiones, se requieren d estructuras iterativas anidadas con sus respectivas d variables para los d índices.
2.8 ¿Programación orientada a objetos?
La idea de clases y objetos surge como una evolución en los mecanismos de abstracción que se han desarrollado en la historia de la programación.
Al inicio, los lenguajes solo ofrecían tipos de datos primitivos, como números o caracteres, que permiten representar información muy básica.
Más adelante aparecieron estructuras como los arreglos, que ampliaron la capacidad de trabajar con colecciones de datos homogéneos.
Sin embargo, esta manera de organizar la información resultaba insuficiente para modelar problemas más complejos del mundo real.
El siguiente paso consistió en buscar estructuras que no solo almacenaran datos, sino que también pudieran expresar de manera integrada qué se puede hacer con esos datos.
De esta necesidad nace la programación orientada a objetos (POO), un enfoque que combina en un mismo concepto la información y las operaciones que le dan sentido.
Esta manera de pensar está directamente inspirada en la forma en que entendemos el mundo: hablamos de entidades u objetos (una célula, un planeta, una especie), cada uno con propiedades que los caracterizan y con comportamientos que los distinguen.
En conjunto, las nociones de clase, objeto, atributos, métodos, encapsulamiento, visibilidad, herencia y polimorfismo transformaron la forma de programar. Con ellas, la programación deja de ser solo una manipulación de números o colecciones de datos, y se convierte en una manera de modelar el mundo y sus relaciones dentro del computador.
2.8.1 ¿Clases y objetos?
Una clase es el molde o plano que describe a un tipo de entidad. Es como un tipo de dato que creamos y personalizamos de acuerdo a nuestras preferencias y necesidades.
En ella se definen los atributos, que corresponden a las propiedades que la identifican, y los métodos, que son las acciones o funciones que puede realizar.
A partir de una clase se pueden generar múltiples objetos, cada uno con valores concretos para sus atributos y con la capacidad de ejecutar los métodos definidos.
Los objetos de un clase serían como las variables de nuestro propio tipo de dato personalizado; variables dispuestas no solo a almacenar datos en sus atributos, sino listas para ejercer sus funcionalidades por medio de la ejecución de sus métodos.
2.8.2 ¿Encapsulamiento y visibilidad?
El concepto de encapsulamiento primero que todo apunta al hecho de que en un solo lado tendremos datos (atributos) y funcionalidades (métodos), pero además se relaciona con el controlar cómo se accede a los atributos de los objetos.
En lugar de permitir que cualquiera manipule directamente la información interna, en la clase se deciden qué aspectos se exponen y cuáles permanecen ocultos. Esto se conoce como visibilidad o ocultamiento. Esto garantiza que los datos se usen de manera coherente y evita que se modifiquen sin control.
En términos prácticos, busca que los objetos se comporten de forma consistente con la definición que les dio origen.
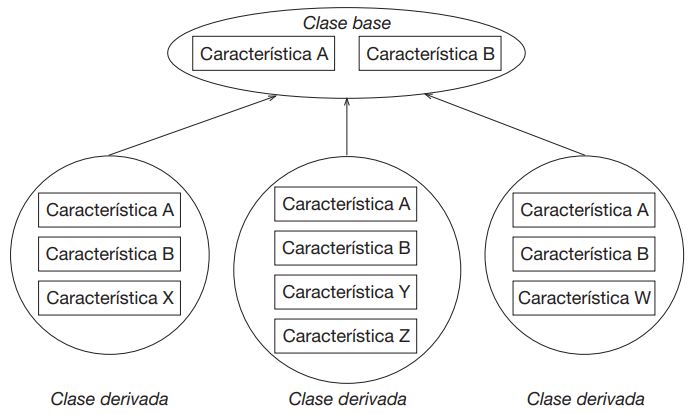
2.8.3 ¿Jerarquía de clases y herencia?
Al trabajar con clases es común descubrir que muchas de ellas comparten atributos y métodos.
En lugar de repetir definiciones, se utiliza la herencia, un mecanismo que permite que una clase nueva aproveche lo ya definido en otra.
La clase que transmite sus características se llama superclase, mientras que la que las recibe se denomina subclase.
La subclase puede conservar los elementos heredados, añadir otros nuevos o modificar lo que necesita adaptar.
De esta manera es posible organizar las clases en jerarquías, donde las definiciones más generales sirven de base para otras más específicas.
Este mecanismo refleja la manera en que solemos estructurar el conocimiento y las categorías en el mundo real: partimos de conceptos amplios y, a partir de ellos, vamos estableciendo distinciones más precisas.
Un ejemplo sencillo de abstracción creciente (de lo general a lo particular) se puede ver en la idea de un vehículo:
A nivel general, todos los vehículos comparten ciertos atributos básicos, como un medio de desplazamiento y una capacidad de transportar personas o cosas.
De esa descripción amplia se pueden derivar categorías más específicas como automóvil, bicicleta o barco.
Cada una de estas subcategorías conserva lo que caracteriza a un vehículo en general, pero añade sus propias propiedades y comportamientos:
- un automóvil puede tener motor y ruedas,
- una bicicleta pedales y cadenas,
- un barco casco y timón.
Así, lo general sirve como base y lo particular agrega las diferencias necesarias. Este es el mismo principio que guía las jerarquías de clases en programación orientada a objetos.
La herencia no solo evita duplicar definiciones. También permite organizar el conocimiento de forma ordenada, reflejando cómo pensamos y clasificamos la realidad, y facilitando la creación de sistemas complejos que siguen siendo comprensibles y coherentes.
2.8.4 ¿Polimorfismo?
Otro concepto clave es el polimorfismo.
Con él, diferentes clases pueden compartir un mismo nombre de método, pero la acción concreta que se realiza depende de la clase del objeto que activa la funcionalidad (que ejecuta el método).
Imagina la acción “abrir”:
El mismo término se aplica a contextos muy distintos:
- abrir una puerta,
- abrir un libro,
- abrir un archivo digital.
La forma de invocar la acción sería la misma —“abrir”—, pero lo que realmente sucede depende del objeto con el que se está trabajando.
- En un caso se gira una manija,
- en otro se separan páginas,
- y en otro se carga información en una pantalla.
Ese es el sentido del polimorfismo en programación orientada a objetos: un mismo método o acción puede aplicarse de manera uniforme, pero su ejecución concreta se adapta a la naturaleza del objeto que la recibe.
El polimorfismo unifica la interacción con objetos distintos y simplifica la manera de pensar su uso, lo que refuerza la abstracción.
2.9 ¿R, herramienta de análisis o lenguaje de programación?
The Comprehensive R Archive Network (página oficial de R):
RStudio Desktop - Posit:
https://posit.co/download/rstudio-desktop/
Instalación de R | RStudio del profesor Juan Sosa:
Tutorial R-Commander (COMPLETO) de “Eolis 97”:
https://youtube.com/playlist?list=PLBkQ_rkI6r7BmUGbwPCloYjXcq_ZKzVsT
En este enlace encontrarán una revisión de los elementos básicos de programación imperativa estructurada procedimental (PIEP) y de programación orientada a arreglos (POA) para poder realizar una implementación en R (R como lenguaje de programación, NO como herramienta de cálculo o de análisis de datos):
En este enlace encontrarán una revisión de algunos elementos disponibles (preconstruidos) en R, que le podrían ser de utilidad a una persona que desee usar dicho software como una herramienta de cálculo o de análisis de datos (NO como un lenguaje de programación):
2.10 ¿Python, herramienta de análisis o lenguaje de programación?
Minicurso de ciencia de datos
Día 1: Introducción a Python (Aprendizaje Profundo - Jun 27, 2023 - 2:18:34)
En este enlace encontrarán una revisión de los elementos básicos de programación imperativa estructurada procedimental (PIEP) para poder realizar una implementación en Python (Python como lenguaje de programación bajo el paradigma estructurado procedimental, NO como herramienta de cálculo o de análisis de datos):
En este enlace encontrarán una revisión de elementos básicos necesarios para poder realizar una implementación de clases y objetos en Python (Python como lenguaje de programación bajo el paradigma orientado a objetos, NO como herramienta de cálculo o de análisis de datos):
En este enlace encontrarán una revisión de algunos elementos disponibles (preconstruidos) en Python, que les podrían ser de utilidad a la hora de usar dicho software simplemente como una herramienta de cálculo o de análisis de datos (NO como un lenguaje de programación):
En este enlace encontrarán una revisión de algunas clases de particular importancia o relevancia, incluidas dentro de Python. Estás clases tienen objetivos particulares muy puntuales y permiten a los programadores o usuarios de Python hacer ciertas tareas generales y específicas, bajo la premisa que se entiende cómo usar Python bajo el paradigma orientado a objetos:
https://cjtorresj.quarto.pub/ple/11-Python-some-classes.html