9 Aprendizaje supervisado básico
Fundamentos aplicados de aprendizaje supervisado básico
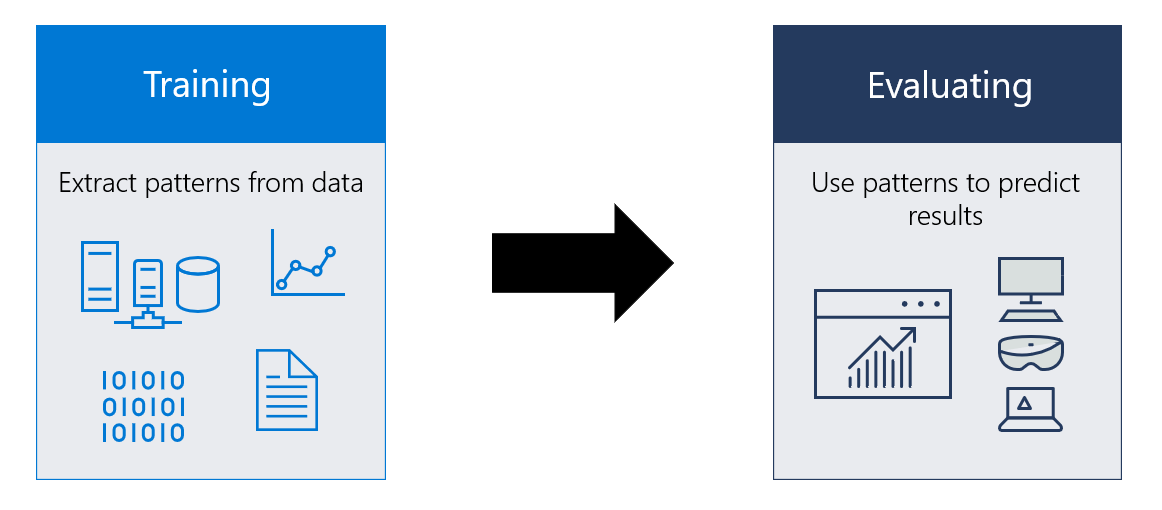
En aprendizaje supervisado, los datos disponibles incluyen tanto las variables predictoras como la variable de respuesta o target, lo que permite entrenar modelos capaces de aprender la relación funcional entre ambas partes.
El propósito central es construir una función de predicción que, a partir de las características observadas, estime adecuadamente el valor de la respuesta para nuevas observaciones. Este proceso implica equilibrar la capacidad de ajuste a los datos conocidos y la habilidad de generalizar hacia datos no observados.
Desde una perspectiva estadística, el aprendizaje supervisado puede entenderse como el problema de estimación de una función desconocida f, tal que Y = f(X).
A partir de un conjunto de entrenamiento \{(x_i, y_i)\}_{i=1}^{n}, el modelo busca encontrar una función \hat{f} que minimice el error de predicción en datos futuros.
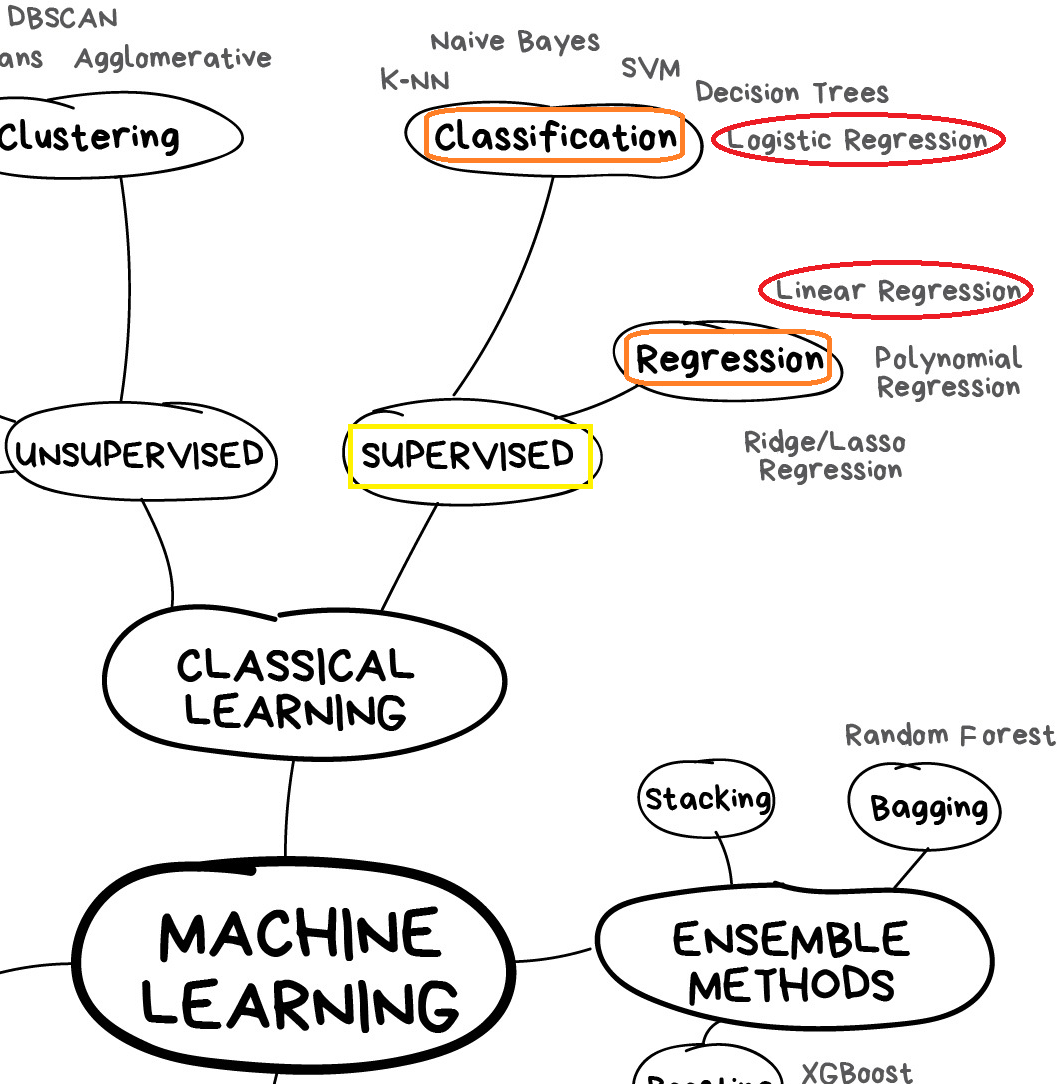
Dentro de este enfoque se distinguen dos grandes tareas fundamentales:
Regresión: cuando la variable de respuesta es numérica o continua, y se busca estimar su valor esperado en función de los predictores.
Clasificación: cuando la variable de respuesta es categórica o discreta, y el objetivo consiste en asignar cada observación a una categoría o clase determinada.
El rendimiento de los modelos supervisados depende de la calidad de los datos, la adecuación de las variables seleccionadas, y el criterio de evaluación utilizado para medir el error o la exactitud de las predicciones.
En consecuencia, el aprendizaje supervisado no solo requiere procedimientos de ajuste matemático, sino también una comprensión crítica de la estructura de los datos y de la naturaleza del problema, lo que permite seleccionar modelos pertinentes y establecer interpretaciones válidas.
Para mejorar la generalización y evitar problemas como el sobreajuste (overfitting), se utilizan técnicas como la selección de características (feature selection), la extracción de características (feature extraction), la regularización y la validación cruzada (cross-validation).
El entrenamiento de modelos supervisados requiere definir una función de pérdida (loss function) que cuantifique el error entre las predicciones del modelo (\hat{y}_i) y los valores observados (y_i).
Posteriormente, se emplean algoritmos de optimización para minimizar esta función de pérdida y ajustar los parámetros del modelo, es decir, los parámetros asociados a la función \hat{f}.
Los modelos lineales constituyen una de las herramientas fundamentales en estadística y machine learning.
Su importancia radica en su capacidad para modelar relaciones entre variables, permitiendo realizar inferencias, predicciones y entender patrones en los datos.
A pesar de su aparente simplicidad, los modelos lineales son una piedra angular en muchas aplicaciones.
Los modelos lineales suelen proporcionar un alto nivel de interpretabilidad y de eficiencia computacional, lo que los hace una opción fundamental en muchos contextos.
El término “lineal” en este caso se refiere a la relación matemática entre la variable de respuesta y las variables explicativas, que se expresa como una combinación lineal de los parámetros desconocidos.
No obstante, esto no implica que los datos deban exhibir un comportamiento estrictamente lineal, sino que la estructura del modelo debe ser lineal en los parámetros.
Esta característica permite una interpretación clara de los coeficientes y facilita la estimación mediante métodos eficientes como los mínimos cuadrados y la máxima verosimilitud.
9.1 Problemas de regresión
Los problemas de regresión surgen cuando el objetivo es modelar y predecir una variable continua a partir de un conjunto de variables explicativas.
En términos generales, estos modelos buscan capturar la relación entre una variable de respuesta cuantitativa Y y un conjunto de predictores X_1, X_2, \dots, X_p, con el fin de comprender su influencia y realizar “predicciones” para nuevas observaciones.
Desde el enfoque estadístico, la regresión se centra en modelar la media condicional de Y dado X, permitiendo la inferencia sobre los coeficientes y la incertidumbre en las estimaciones.
Desde machine learning, la regresión se entiende como una tarea de aprendizaje supervisado, donde el objetivo es minimizar la diferencia entre las predicciones y los valores reales.
El modelo de regresión lineal simple es el punto de partida en este contexto, donde la relación entre la variable respuesta cuantitativa y un único predictor se expresa mediante una ecuación lineal con un término de error aleatorio.
Y = \beta_0 + \beta_1 X + \varepsilon
A partir de este concepto, se extiende la regresión lineal múltiple, permitiendo la inclusión de múltiples predictores y proporcionando una herramienta más flexible para modelar fenómenos complejos.
Y = \beta_0 + \beta_1 X_1 + \dots + \beta_k X_k + \varepsilon
Modelo cuadrático:
Y = \beta_0 + \beta_1 X + \beta_2 X^2 + \varepsilon
Tome X_1 = X y X_2 = X^2.
Modelo cúbico:
Y = \beta_0 + \beta_1 X + \beta_2 X^2 + \beta_3 X^3 + \varepsilon
Tome X_1 = X, X_2 = X^2 y X_3 = X^3.
Modelo polinómico de orden q:
Y = \beta_0 + \beta_1 X + \dots + \beta_q X^q + \varepsilon
Tome X_1 = X, \dots, y X_q = X^q.
Modelo inverso:
Y = \beta_0 + \frac{\beta_1}{X} + \varepsilon
Tome X_1 = 1/X.
Modelo logarítmico:
Y = \beta_0 + \beta_1 \log(X) + \varepsilon
Tome X_1 = \log(X).
Modelo de segundo orden completo:
Y = \beta_0 + \beta_1 X_A + \beta_2 X_B + \beta_3 X_A X_B + \beta_4 X_A^2 + \beta_5 X_B^2 + \varepsilon
Tome X_1 = X_A, X_2 = X_B, X_3 = X_A X_B, X_4 = X_A^2 y X_5 = X_B^2.
Modelo de potencia:
Y = \beta_0 X^{\beta_1} \varepsilon
Transforme a \ln(Y) = \ln(\beta_0) + \beta_1 X + \ln(\varepsilon) y tome Y^* = \ln(Y) y \beta_0^* = \ln(\beta_0).
Modelo compuesto:
Y = \beta_0 \beta_1^{X} \varepsilon
Transforme a \ln(Y) = \ln(\beta_0) + \ln(\beta_1) X + \ln(\varepsilon).
Modelo exponencial general o de crecimiento:
Y = e^{\beta_0 + \beta_1 X + \varepsilon}
Transforme a \ln(Y) = \beta_0 + \beta_1 X + \varepsilon.
Modelo exponencial:
Y = \beta_0 e^{\beta_1 X + \varepsilon}
o
Y = \beta_0 e^{\beta_1 X} \varepsilon
Transforme a \ln(Y) = \ln(\beta_0) + \beta_1 X + \varepsilon o \ln(Y) = \ln(\beta_0) + \beta_1 X + \ln(\varepsilon).
Modelo de curva-s:
Y = e^{\beta_0 + \beta_1/X + \varepsilon}
Transforme a \ln(Y) = \beta_0 + \beta_1 X_1 + \varepsilon, con X_1 = 1/X.
En regresión, se utilizan métricas como el error cuadrático medio (Mean Squared Error, MSE) o el error absoluto medio (Mean Absolute Error, MAE).
Además, elementos como la regularización (ridge, lasso, etc.) son esenciales para mejorar la capacidad de generalización del modelo y evitar problemas como el sobreajuste (overfitting).
Cuadernos computacionales:
9.2 Problemas de clasificación
Los problemas de clasificación aparecen cuando la variable respuesta es categórica, es decir, cuando se desea asignar una observación (individuo / registro / realización, instancia) a una de varias categorías, clases o etiquetas posibles.
A diferencia de la regresión, donde se predicen valores numéricos, en la clasificación el objetivo es estimar la probabilidad de pertenencia a cada clase y asignar la categoría más probable a una nueva observación.
Desde la estadística, los modelos de clasificación pueden interpretarse como una extensión de los modelos lineales a variables respuesta discretas, a menudo utilizando modelos como la regresión logística o los modelos lineales generalizados (Generalized Linear Models, GLMs).
En machine learning, la clasificación se entiende como una tarea supervisada donde se busca minimizar funciones de pérdida específicas para datos no continuos.
En relación a lo anterior, la evaluación de modelos de clasificación requiere métricas distintas a las usadas en regresión, debido a que las predicciones son de naturaleza categórica. Se emplean métricas como la matriz de confusión, la exactitud (accuracy), la precisión (precision), la recuperación (recall), la puntuación F1 (F1-score), entre otras.
Uno de los modelos más utilizados para resolver problemas de clasificación en dos categorías (binaria) es la regresión logística, que extiende la idea de los modelos lineales, al relacionar una combinación lineal de los predictores con la probabilidad de pertenencia a una de las dos categorías, mediante la función logística \left(\phi()\right) / sigmoide \left(\sigma()\right).
\begin{aligned} p &= \frac{1}{1 + e^{-\left(\beta_0 + \beta_1 X_1 + \dots + \beta_k X_k\right)}} \\ \ln \left( \frac{p}{1-p} \right) &= \beta_0 + \beta_1 X_1 + \dots + \beta_k X_k \end{aligned}
Cuadernos computacionales:
Para casos con más de dos categorías, se pueden emplear estrategias como la regresión logística multinomial u otros modelos.
9.3 Ampliar o complementar
El contenido de toda la sección se puede ampliar o complementar con lo que se encuentra en:
Cuaderno computacional: Modelos lineales generalizados (MLG)
Cuaderno computacional: MLG: Modelos de regresión binomial y logístico
Scikit-learn: Machine Learning in Python, 1.1. Linear Models https://scikit-learn.org/stable/modules/linear_model.html