El aprendizaje no supervisado es una rama fundamental del machine learning (aprendizaje de máquinas o aprendizaje automático) que se caracteriza por trabajar con datos sin etiquetar.
A diferencia del aprendizaje supervisado, no se dispone de una variable de respuesta o target que oriente el entrenamiento del modelo / “máquina” / algoritmo / función.
En este contexto, el objetivo principal es descubrir patrones, estructuras y relaciones ocultas en los datos.
Desde una perspectiva estadística, el aprendizaje no supervisado puede entenderse como el problema de identificar patrones o relaciones a partir de un conjunto de observaciones (individuos, registros, realizaciones o instancias).
El modelo busca encontrar estructuras que permitan representar los datos de manera más sencilla o informativa.
Antes de aplicar cualquier método, es esencial realizar una exploración inicial de los datos.
Esta exploración debe comenzar con el análisis univariado y luego con el bivariado, como primera aproximación para comprender el comportamiento de las variables y sus relaciones más simples.
A partir de esta base, el análisis exploratorio puede ampliarse con procedimientos más complejos que profundicen en la estructura de los datos y en la identificación de patrones o relaciones de mayor nivel.
En conjunto, este proceso permite detectar errores, comprender la variabilidad, reconocer tendencias generales y obtener una visión preliminar del conjunto de datos, así como de posibles transformaciones útiles para el análisis o la resolución del problema planteado.
De esa comprensión depende la solidez del análisis posterior, ya que los métodos o procedimientos aplicados solo pueden ofrecer resultados útiles cuando parten de una lectura cuidadosa y bien fundamentada de la información disponible.
Recordemos que una tabla de datos básica tiene en filas las unidades estadísticas o individuos (observaciones, instancias o registros), y en columnas las variables (características, atributos o features). Así mismo, recordemos su relación con el objeto matemático llamado matriz.
“La Universidad Nacional de Colombia selecciona, a los estudiantes que se admiten en cada semestre mediante la aplicación de un examen de admisión estructurado en cinco áreas: matemáticas, ciencias, sociales, textual e imágenes… Para este ejemplo se toman los resultados de los 445 admitidos a las siete carreras de la Facultad de Ciencias del primer semestre de 2013… La hoja de datos retenida para el ejemplo tiene en las columnas: la carrera, los resultados del examen en cada área y global, algunas variables sociodemográficas…”
Pardo, C. (2020). Estadística descriptiva multivariada. [online] Bogotá, Colombia: Universidad Nacional de Colombia. https://repositorio.unal.edu.co/handle/unal/79914
# 2 cifras significativas y sin notación científica:
options(digits = 2, scipen = 999)
# carga de paquetes
if(!require(FactoClass)){
install.packages("FactoClass")
library(FactoClass)
}
# cargar data.frame admitidos de FactoClass
data(admi) Debemos tener claro cuáles son los individuos (o unidades estadísticas), las variables, y las escalas de medida de todas las variables.
Una adecuada representación es importante para observar y trasmitir adecuadamente información valiosa presente en nuestros datos.
Dicha representación suele depender de la escala de medida de la variable.
Representación tabular:
| categorias | frec.abs. | frec.rel. | porcent. |
|---|---|---|---|
| Biol | 63 | 0.14 | 14 |
| Esta | 66 | 0.15 | 15 |
| Farm | 73 | 0.16 | 16 |
| Fisi | 82 | 0.18 | 18 |
| Geol | 45 | 0.10 | 10 |
| Mate | 53 | 0.12 | 12 |
| Quim | 63 | 0.14 | 14 |
| TOTAL | 445 | 1.00 | 100 |
¿Qué carrera tiene la mayor cantidad (o porcentaje) de estudiantes admitidos? ¿cuántos son? ¿qué carrera la menor cantidad (o porcentaje)? ¿qué porcentaje es?
Representación gráfica (diagrama de barras):
Representación gráfica (diagrama de pareto):
Representación gráfica (diagrama de torta):
Representación tabular:
| categorias | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| E0 | 2 | 0.00 | 2 | 0.00 |
| E1 | 36 | 0.08 | 38 | 0.09 |
| E2 | 141 | 0.32 | 179 | 0.40 |
| E3 | 185 | 0.42 | 364 | 0.82 |
| E4 | 72 | 0.16 | 436 | 0.98 |
| E5 | 8 | 0.02 | 444 | 1.00 |
| E6 | 1 | 0.00 | 445 | 1.00 |
| TOTAL | 445 | 1.00 | NA | NA |
¿Cuántos tienen estrato 2 o inferior? ¿qué porcentaje tiene estrato 5 o superior?
Representación gráfica (diagrama de barras):
Representación gráfica (diagrama de torta):
Por ejemplo, la variable es número de hijos en el hogar para 1500 hogares.
Representación tabular:
| valores | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| 0 | 419 | 0.28 | 419 | 0.28 |
| 1 | 255 | 0.17 | 674 | 0.45 |
| 2 | 375 | 0.25 | 1049 | 0.70 |
| 3 | 215 | 0.14 | 1264 | 0.84 |
| 4 | 127 | 0.09 | 1391 | 0.93 |
| 5 | 54 | 0.04 | 1445 | 0.96 |
| 6 o más | 55 | 0.04 | 1500 | 1.00 |
¿Qué porcentaje de los hogares tiene menos de dos hijos? ¿La mitad de las familias que menos hijos tiene, entre cuántos y cuántos hijos tiene?
Representación gráfica (diagrama de barras):
Representación gráfica (diagrama de torta):
¿Para una variable con escala de medida de razón haríamos todo igual (representaciones tabulares y gráficas) que como lo hicimos para una variable con escala de medida de intervalo?
¿Qué pasaría si cada valor tomado por la variable con escala de medida de razón lo consideramos una fila de una representación tabular asociada a la variable?
Teniendo en cuenta que nos tocaría trabajar con intervalos, ¿qué mecanismo o qué criterio debemos usar para escoger o definir esos intervalos?
Representación tabular:
| intervalo | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| [400,500] | 4 | 0.009 | 4 | 0.01 |
| (500,600] | 22 | 0.049 | 26 | 0.06 |
| (600,700] | 166 | 0.373 | 192 | 0.43 |
| (700,800] | 187 | 0.420 | 379 | 0.85 |
| (800,900] | 55 | 0.124 | 434 | 0.98 |
| (900,1000] | 5 | 0.011 | 439 | 0.99 |
| (1000,1100] | 5 | 0.011 | 444 | 1.00 |
| (1100,1200] | 1 | 0.002 | 445 | 1.00 |
Representación gráfica (histograma):
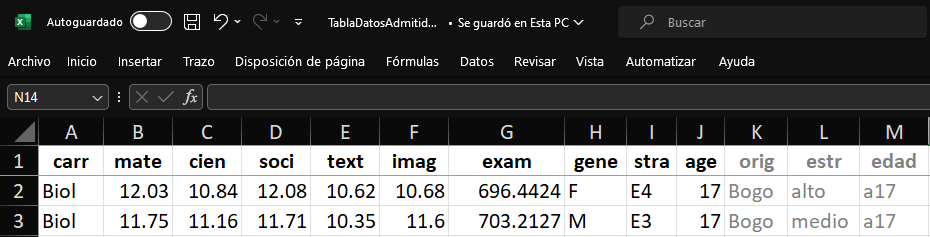
¿Cómo podría responder preguntas como esta o similares, usando los datos que se tienen (por ejemplo, de los puntajes en el examen)?: Si se decide proporcionar apoyo adicional al 25% de los estudiantes con los puntajes más bajos, ¿cuál sería el puntaje de corte para proporcionar o no ese apoyo?
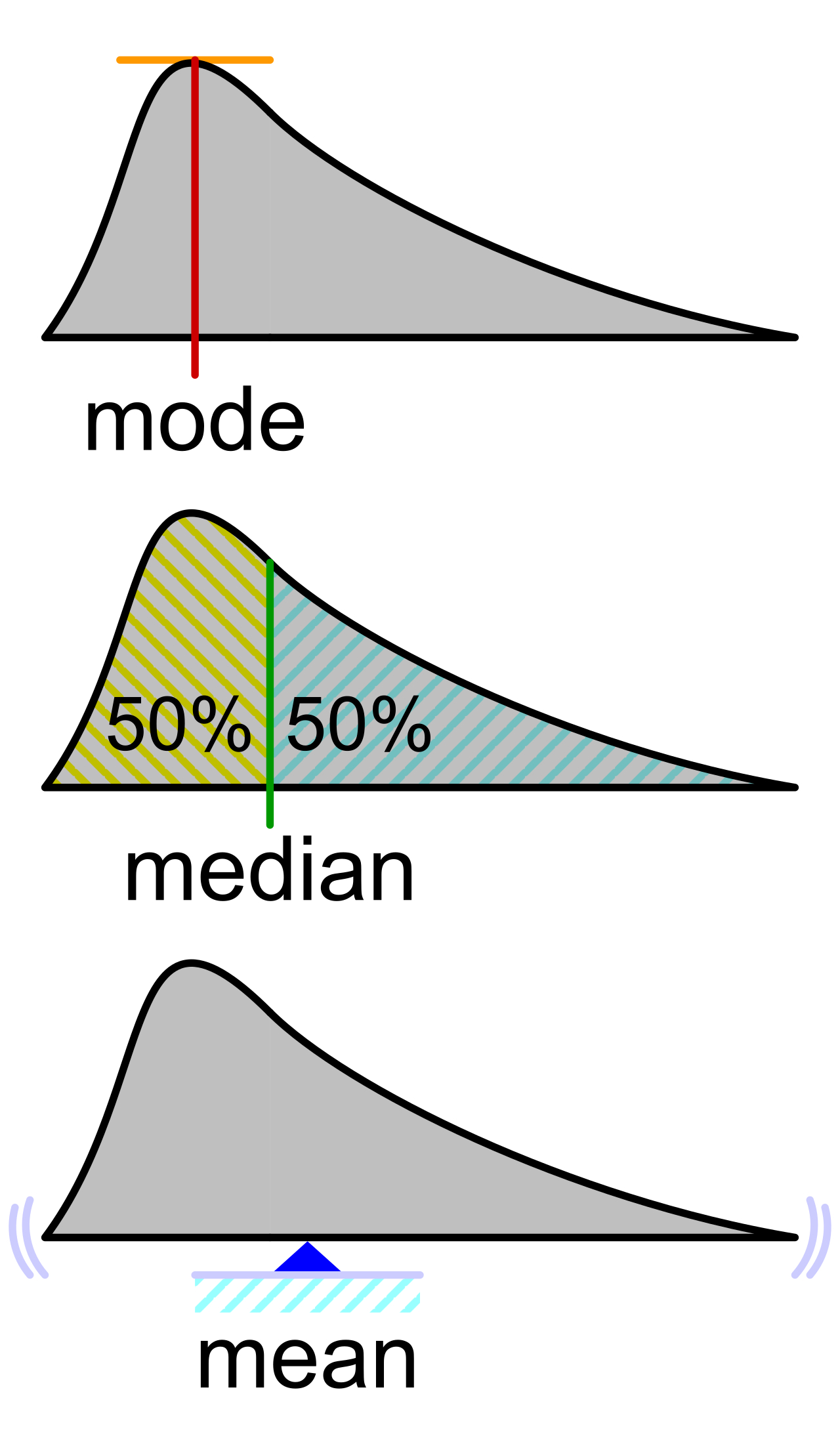
Por ejemplo, el cuantil 0.12 es el valor para la variable, que marca un corte de tal manera que el 12\% de los valores que se tienen de la variable son menores o iguales al valor del cuantil, y el 88\% restante de los valores de la variable son mayores o iguales al valor del cuantil.
Existen una serie de cuantiles importantes o de uso más frecuente:
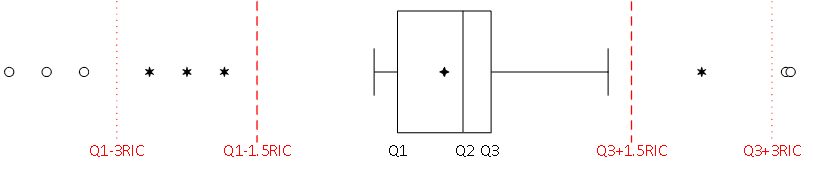
Cuartiles: Dividen los datos en cuatro partes iguales. Corresponden a los cuantiles 0.25 (Q_1), 0.50 (Q_2) y 0.75 (Q_3).
Quintiles: Dividen los datos en cinco partes iguales
Deciles: Dividen los datos en diez partes iguales
Percentiles: Dividen los datos en cien partes iguales. Corresponden a los cuantiles 0.01, 0.02, …, 0.98 y 0.99
¿Cómo calcular?:
En Hyndman, R. J., & Fan, Y. (1996). Sample quantiles in statistical packages. The American Statistician, 50(4), 361-365. hacen una revisión y comparación de nueve (9) alternativas de cálculo para los cuantiles (desde la teoría, cada una tiene sus ventajas y desventajas).
“Alternativa 7” es la que usan en:
PERCENTILE.INC (antes era la función PERCENTILE).quantile, pero se puede seleccionar cualquiera de las nueve del artículo mencionado (cambiando el valor para el parámetro type).Para la variable examen, se tiene que:
q <- quantile(admi$exam, type = 7)| 0% | 25% | 50% | 75% | 100% |
|---|---|---|---|---|
| 477 | 667 | 710 | 761 | 1151 |
Existen varias medidas descriptivas que representan la centralidad de los datos, cada una de ellas de diferente manera.
Moda:
Categoría(s) o valore(s) que tiene(n) la frecuencia más alta.
Mediana:
La mediana es el número de la mitad, el que divide los valores ordenados de una variable en dos partes iguales (es el cuantil 0.5, es el cuartil 2, es el percentil 50). 50\% de los valores de la variable serían menores o iguales a la mediana y el 50\% restante serían mayores o iguales a la mediana.
Media o promedio:
Es como tomar una partecita, la N-ésima parte, de cada valor y luego sumarlas. También se puede interpretar como un centro de gravedad o punto de equilibrio.
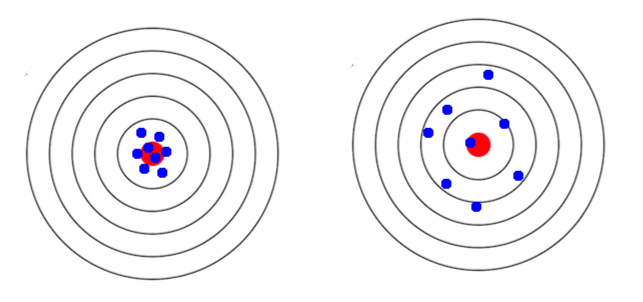
Las medidas descriptivas de dispersión deben poder darnos una idea acerca de que tan concentrados o no están los valores de una variable.
Hay varias opciones, en cada caso identifique en qué unidades estaría la medida y que potenciales ventajas y desventajas podría tener.
Rango (R): Diferencia entre el máximo y el mínimo valor de la variable.
Rango intercuartílico (RIC): Diferencia entre el tercer cuartil y el primer cuartil. Magnitud en la cual oscilan el 50\% de los valores centrales que toma la variable.
Varianza poblacional (\sigma^2): Promedio de los cuadrados de las distancias entre cada valor y el promedio.
Desviación estándar poblacional (\sigma): Raíz cuadrada de la varianza.
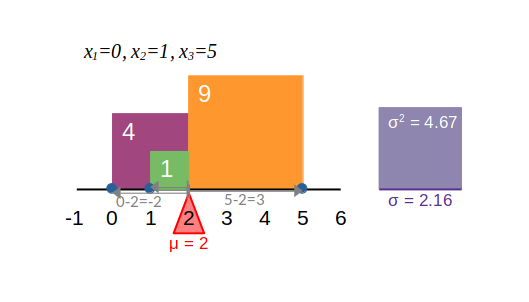
Pero, ¿qué podría representar la varianza y la desviación estándar?
\begin{aligned} \sigma^2 &= \frac{(0 - 2)^2 + (1 - 2)^2 + (5 - 2)^2}{3} = 4.6667 \\ \sigma^2 &= \frac{(x_1 - \mu)^2 + (x_2 - \mu)^2 + \dots + (x_N - \mu)^2}{N} \end{aligned}
Coeficiente de variación:
Es el resultado de tomar la desviación estándar y dividirla por media (con signo positivo, en caso de que la media sea negativa).
El coeficiente de variación da una idea de variabilidad relativa. Es una cantidad que no tiene asociada alguna unidad (se cancelan las unidades del numerador con las del denominador). Frecuentemente se da o se interpreta como un porcentaje (es un cociente o una razón en donde el numerador no es parte del denominador para que pueda ser considerada como una proporción, y que al multiplicarla por cien se pueda interpretar como un porcentaje). Es útil para comparar la dispersión de dos o más variables.
¿Cuál variable tiene mayor variabilidad (mayor dispersión, menor concentración) entre puntaje en el examen y edad?
Un dato atípico (outlier), bajo la definición de John Tukey, es un valor más pequeño que el resultado de restarle 1.5 veces el rango intercuartilico al primer cuartil o un valor más grande que el resultado de sumarle 1.5 veces el rango intercuartílico al tercer cuartil: x_i<Q_1-(1.5)(\mathrm{RIC}) \quad \text { о } \quad x_i>Q_3+(1.5)(\mathrm{RIC})
Recordemos que para la variable examen, (usando “Alternativa 7”) se tiene que:
| 0% | 25% | 50% | 75% | 100% |
|---|---|---|---|---|
| 477 | 667 | 710 | 761 | 1151 |
entonces, los valores menores a 572.3 y los mayores a 855.8 serían atípicos.
El diagrama de caja (boxplot) es una representación gráfica que se construye principalmente a partir de los cuartiles 1, 2 y 3. En el diagrama de caja también se muestran los valores atípicos, si los hay.
Para la variable examen (los cortes para los atípicos tienen una pequeña variación metodológica con respecto a la definición dada por John Tukey):
Para la variable edad (age)
El contenido de esta sección se puede ampliar o complementar con lo que se encuentra en las siguientes páginas:
Probabilidad y Estadística Fundamental (PyEF), Estadística Descriptiva, 2 Univariada:
https://cjtorresj.quarto.pub/pyef/02-estad_descr_univar.html
Estadística Descriptiva Multivariada (companion), Prerequisitos y preliminares, Estadística Descriptiva Univariada:
A continuación se hará una revisión de algunos temas relacionados con el análisis descriptivo de datos de dos variables a la vez. Uno de los principales objetivos de un análisis bivariado es el identificar si hay algún tipo de relación entre las dos variables.
Como cada variable puede ser categórica o numérica, vamos a tener tres posibles escenarios: que las dos variables sean categóricas, que una sea categórica y la otra sea numérica, o que las dos sean numéricas.
Vamos a seguir trabajando con los datos de admitidos.
Representación tabular:
¿Cómo se obtiene la siguiente tabla? ¿qué debemos hacer para obtenerla?
| Biol | Esta | Farm | Fisi | Geol | Mate | Quim | frecGene | |
|---|---|---|---|---|---|---|---|---|
| F | 23 | 17 | 40 | 13 | 8 | 6 | 21 | 128 |
| M | 40 | 49 | 33 | 69 | 37 | 47 | 42 | 317 |
| frecCarr | 63 | 66 | 73 | 82 | 45 | 53 | 63 | 445 |
¿Cuántos admitidos son de género femenino? ¿cuántos son de Geología? ¿cuántos son de género femenino Y de Geología?
Representación tabular:
¿Cómo se obtiene la siguiente tabla? ¿qué debemos hacer para obtenerla?
| Biol | Esta | Farm | Fisi | Geol | Mate | Quim | frecGene | |
|---|---|---|---|---|---|---|---|---|
| F | 0.052 | 0.038 | 0.090 | 0.029 | 0.018 | 0.013 | 0.047 | 0.29 |
| M | 0.090 | 0.110 | 0.074 | 0.155 | 0.083 | 0.106 | 0.094 | 0.71 |
| frecCarr | 0.142 | 0.148 | 0.164 | 0.184 | 0.101 | 0.119 | 0.142 | 1.00 |
¿Qué proporción (porcentaje) de los admitidos son de género femenino? ¿qué proporción (porcentaje) son de Geología? ¿qué proporción (porcentaje) son de género femenino Y de Geología?
Representación gráfica:
¿Qué gráfico(s) podría hacer con la información contenida en esta tabla?
Representación tabular:
¿Cómo se obtiene la siguiente tabla? ¿qué debemos hacer para obtenerla?
| Biol | Esta | Farm | Fisi | Geol | Mate | Quim | Sum | |
|---|---|---|---|---|---|---|---|---|
| F | 0.18 | 0.13 | 0.31 | 0.10 | 0.062 | 0.047 | 0.16 | 1 |
| M | 0.13 | 0.15 | 0.10 | 0.22 | 0.117 | 0.148 | 0.13 | 1 |
| frecCarr | 0.14 | 0.15 | 0.16 | 0.18 | 0.101 | 0.119 | 0.14 | 1 |
¿De los admitidos de género femenino, qué proporción (porcentaje) son de Geología?
Representación gráfica:
¿Cuáles son las franjas que menos coinciden entre lo que se observa para los admitidos de género femenino y lo que se observa para todos los admitidos (es decir para marg (frecCarr))?
Representación tabular:
¿Cómo se obtiene la siguiente tabla? ¿qué debemos hacer para obtenerla?
| Biol | Esta | Farm | Fisi | Geol | Mate | Quim | frecGene | |
|---|---|---|---|---|---|---|---|---|
| F | 0.36 | 0.26 | 0.55 | 0.16 | 0.18 | 0.11 | 0.33 | 0.29 |
| M | 0.64 | 0.74 | 0.45 | 0.84 | 0.82 | 0.89 | 0.67 | 0.71 |
| Sum | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
¿De los admitidos de Geología, qué proporción (porcentaje) son de género femenino?
Representación gráfica:
¿Cuál es la carrera que más difiere en cuanto a la “repartición” por genero, con respecto a marg (frecGene)?
Recordemos que la numérica se puede representar tabular y gráficamente mediante el uso de intervalos (y cada intervalo es como si fuera una categoría, entonces en ese caso es como si tuviéramos dos v. categóricas).
También, podemos conformar grupos de individuos a partir de la categoría que tengan (por ejemplo, un grupo serían los admitidos de género femenino y otro los admitidos de género masculino), y ver comparativamente por grupo, el resultado de un análisis univariado de la variable numérica.
Representación gráfica (boxplots):
¿Existirá alguna manera de representar gráficamente los valores de un par de variables numéricas de nuestro interés (por ejemplo, mate y exam), para un individuo en particular (por ejemplo, el primero de la lista)?
Representación gráfica (diagrama de dispersión):
Covarianza poblacional \left(\sigma_{xy}\right): “Promedio de: el producto de las distancias entre el valor para cada variable y su respectivo promedio”.
\begin{aligned} \sigma_{xy} &= \frac{(12-11.8)(696.4-718.4) + \dots + (11.8-11.8)(740.5-718.4)}{445} \\ &= \frac{(x_1-\mu_x)(y_1-\mu_y) + \dots + (x_N-\mu_x)(y_N-\mu_y)}{N} \end{aligned}
Coeficiente de correlación \left(\rho\right): “Covarianza normalizada”.
\begin{aligned} \rho &= \frac{\sigma_{xy}}{\sigma_x \sigma_y} = \frac{76.37}{(1.28) (8020.65)} = 0.75 \end{aligned}
Coeficiente de determinación \left(R^2\right): “Proporción explicada por la relación lineal”.
\begin{aligned} R^2 &= \rho^2 = (0.75)^2 = 0.57 \end{aligned}
Diagramas de dispersión con sus respectivos coeficientes de correlación:
Puede que exista una relación entre las dos variables pero que esta en realidad no sea, ni directamente proporcional, ni inversamente proporcional, es decir, en realidad no es lineal (¿será otro tipo de relación? ¿cuadrática? ¿cúbica? ¿exponencial?).
El contenido de esta sección se puede ampliar o complementar con lo que se encuentra en las siguientes páginas:
Probabilidad y Estadística Fundamental (PyEF), Estadística Descriptiva, 3 Bivariada:
Estadística Descriptiva Multivariada (companion), Prerequisitos y preliminares, Estadística Descriptiva Bivariada: