6 Bajo normalidad

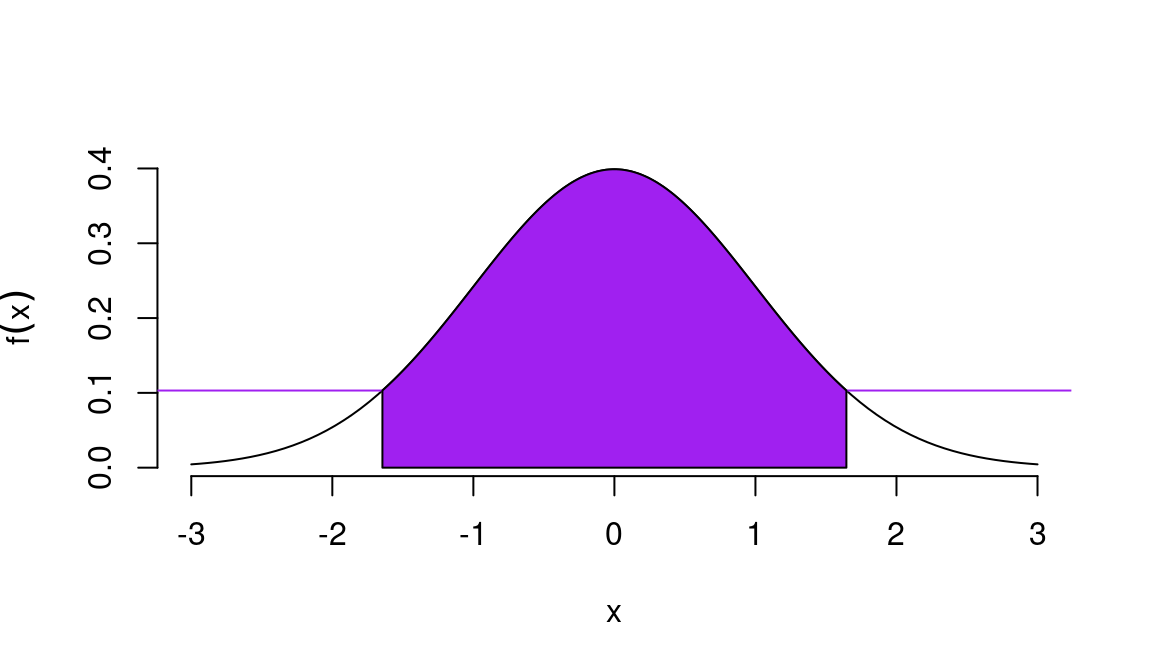
En esta sección se hará una revisión de algunos resultados relacionadas con la estimación por intervalo (intervalos de confianza) cuando se supone que las muestras aleatorias provienen de poblaciones con distribución normal.

En adelante se utilizará la siguiente notación, tal y como se representa en el siguiente gráfico.

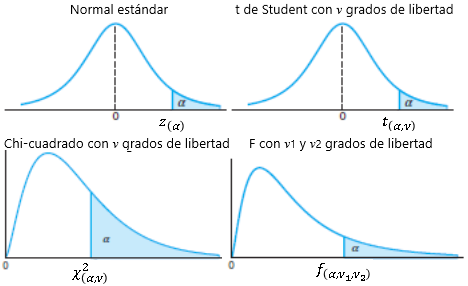
Note la relación entre la notación que se suele utilizar para los cuantiles y esta notación adicional (mi intención es tener una pequeña variante en la notación que permita diferenciar y no confundir una cosa con otra):

\begin{aligned} z_{1 - \alpha} &= z_{(\alpha)} \\ t_{1-\alpha,\nu} &= t_{(\alpha,\nu)} \\ \chi^2_{1-\alpha,\nu} &= \chi^2_{(\alpha,\nu)} \\ f_{1-\alpha,\nu_1,\nu_2} &= f_{(\alpha,\nu_1,\nu_2)} \end{aligned}

Adicionalmente, recordemos que:

Si Z_1, \dots, Z_\nu son variables aleatorias normales estándar independientes, entonces \sum_{i=1}^{\nu} Z_i^2 \sim \chi^2_\nu
Si Z es una variable aleatoria normal estándar, V es una variable aleatoria chi-cuadrado con \nu grados de libertad, y Z y V son independientes, entonces \frac{Z}{\sqrt{V/\nu}} \sim t_\nu
Si W es una variable aleatoria chi-cuadrado con \nu_1 grados de libertad, V es una variable aleatoria chi-cuadrado con \nu_2 grados de libertad, y W y V son independientes, entonces \frac{W/\nu_1}{V/\nu_2} \sim F_{\nu_1,\nu_2}
Si X \sim \mathcal{N}(\mu, \sigma^2), entonces,
- \bar{X} y S^2 son variables aleatorias independientes (naturalmente, \bar{X} y M^{(2)} también lo son).
- \bar{X} \sim \mathcal{N}\left(\mu, \frac{\sigma^2}{n}\right)
- \frac{\sum_{i=1}^{n} \left( X_i - \mu \right)^2}{\sigma^2} \sim \chi_{n}^2
- \frac{\sum_{i=1}^{n} \left( X_i - \bar{X} \right)^2}{\sigma^2} = \frac{n M^{(2)}}{\sigma^2} = \frac{(n-1) S^2}{\sigma^2} \sim \chi_{n-1}^2

6.1 Media

6.1.1 Varianza conocida

Para una muestra aleatoria de una población Normal de media \mu = \theta y varianza \sigma^2 conocida; usando el método de la variable pivote, se deduce que, \left( \bar{X} - (b)\left(\frac{\sigma}{\sqrt{n}}\right) , \bar{X} + (-a)\left(\frac{\sigma}{\sqrt{n}}\right) \right) es un intervalo de confianza bilateral del 100(1-\alpha)\% para \theta, donde a y b serían cuantiles de la distribución normal estándar tales que \Phi(b) - \Phi(a) = 1 - \alpha, siendo \Phi(.) la función de distribución acumulativa normal estándar (a partir de la realización del Ejercicio 5.1 y del Ejercicio 5.2).

Note que:

Un estimador puntual de \theta \left(\bar{X}\right) es un punto de referencia para el intervalo (el intervalo está definido alrededor de ese punto).
El límite superior está a una distancia de -a veces la desviación estándar del mencionado estimador puntual (desviación estándar del estimador puntual = error estándar del estimador: SE\left[\bar{X}\right] = SD\left[\bar{X}\right] = \sigma/\sqrt{n}) y el límite inferior está a una distancia de b veces ese error estándar.
Si se utiliza \bar{x} para estimar \theta, se tiene un 100(1-\alpha)\% de confianza en que la distancia entre \bar{x} y \theta no excederá \max\left\{ (-a) \frac{\sigma}{\sqrt{n}}, (b) \frac{\sigma}{\sqrt{n}}\right\}, a veces denominado error máximo admisible o margen de error.
Además, se tiene un 100(1-\alpha)\% de confianza en que el margen de error no excederá una cantidad dada e, cuando el tamaño de muestra es por lo menos de, n = \left\lceil \left( \max\left\{(-a)\frac{\sigma}{e}, (b) \frac{\sigma}{e}\right\} \right)^2 \right\rceil. Claramente, para calcular el anterior tamaño de muestra se requiere un valor para \sigma. En la práctica, usualmente, dicho valor se desconoce por completo y en ese caso la recomendación es usar una desviación estándar estimada proveniente de un estudio previo o de una muestra piloto o preliminar.

Por otra parte, al tomar diferentes valores para a y b obtenemos infinitos intervalos de confianza del 100(1-\alpha)\% para \theta. Si se desea el intervalo de confianza de menor longitud posible entonces, \begin{aligned} \min_{a < b} \left\{ T^{(2)} - T^{(1)} \right\} &= \min_{a < b} \left\{ \bar{X} + (-a) \frac{\sigma}{\sqrt{n}} - \left( \bar{X} - (b) \frac{\sigma}{\sqrt{n}} \right) \right\} \\ &= \min_{a < b} \left\{ (-a) \frac{\sigma}{\sqrt{n}} + (b) \frac{\sigma}{\sqrt{n}} \right\} \\ &= \min_{a < b} \left\{ (b-a) \frac{\sigma}{\sqrt{n}} \right\} = \min_{a < b} \left\{ b-a \right\} \end{aligned} es decir, minimizar la longitud del intervalo es equivalente a minimizar b-a, con la condición o restricción de que \Phi(b) - \Phi(a) - 1 + \alpha = 0 (y de que a < b).

Derivando la función a minimizar con respecto a b, e igualando a cero se tiene que, \frac{\partial}{\partial b} (b-a) = 1 - \frac{\partial a}{\partial b} = 0, al derivar la restricción con respecto a b se tiene que, \begin{aligned} \frac{\partial}{\partial b} (\Phi(b) - \Phi(a) - 1 + \alpha) &= \frac{\partial}{\partial b} 0 \\ \phi(b) - \phi(a) \frac{\partial a}{\partial b} &= 0 \\ \frac{\partial a}{\partial b} &= \frac{\phi(b)}{\phi(a)} \end{aligned} y sustituyendo, \begin{aligned} 1 - \frac{\partial a}{\partial b} &= 0 \\ 1 - \frac{\phi(b)}{\phi(a)} &= 0 \\ \frac{\phi(b)}{\phi(a)} &= 1 \\ \phi(b) &= \phi(a) \end{aligned} Como la función de densidad normal estándar (\phi(.)) es simétrica, los únicos a y b tales que a < b y \phi(b) = \phi(a) son b = -a = z_{(\alpha/2)} = \Phi^{-1}(\alpha/2) \left( P \left[Z > z_{(\alpha/2)}\right] = \alpha/2 \right).

Código

alpha = 0.1; z <- qnorm(1-alpha/2); f.z <- dnorm(z)
curve(dnorm(x), -3, 3, bty="n", ylab = expression(f(x)))
abline(h = f.z, col = "purple")
x <- seq(-z, z, 0.01); y <- dnorm(x)
polygon(c(z,z,-z,-z,x), c(f.z,0,0,f.z,y), col = "purple")

En conclusión, el intervalo de confianza bilateral, de longitud mínima, del 100(1-\alpha)\% para \theta, bajo el supuesto de que la varianza \sigma^2 es conocida, es, \left( \bar{X} - z_{(\alpha/2)}\frac{ \sigma}{\sqrt{n}} , \bar{X} + z_{(\alpha/2)}\frac{ \sigma}{\sqrt{n}} \right)

Ejercicio 6.1 Para el intervalo de confianza bilateral de longitud mínima:

¿Cuál sería la fórmula del respectivo margen de error?
¿Cuál sería la fórmula para calcular el menor tamaño de muestra que se requeriría para no pasarme de un cierto margen de error dado?

Ejercicio 6.2 (D. Anderson, D. Sweeney, T. Williams, J. Camm - Estadística para Negocios y Economía. 11ra Edición, Cengage Learning (2012). Capítulo 8. Ejercicio 6.) The Wall Street Journal informó que en 2008 los accidentes automovilísticos le costaron \$162 mil millones a Estados Unidos (The Wall Street Journal, 5 de marzo de 2008). El costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida, fue considerado de \$1599. Suponga que este costo promedio se basó en una muestra de 50 personas que estuvieron involucradas en dichos percances y que la desviación estándar poblacional es \$600.

Proporcione una estimación mediante un intervalo de confianza de 90\% para el costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida.
¿Cuál es el margen de error para un intervalo de 90\% de confianza?
¿Qué recomendaría si el estudio requiriera un margen de error de \$50 o menos?
¿Qué le sucede a la amplitud del intervalo de confianza a medida que el nivel de confianza aumenta (90\%, 95\%, 99\%)?
¿Qué le sucede a la amplitud del intervalo de confianza a medida que el tamaño de muestra aumenta (50, 100, 500)?

Ejercicio 6.3 (D. Anderson, D. Sweeney, T. Williams, J. Camm - Estadística para Negocios y Economía. 11ra Edición, Cengage Learning (2012). Capítulo 8. Ejercicio 50.) Se efectúan pruebas de rendimiento de gasolina con un determinado modelo de automóvil. Si se desea dar un intervalo de confianza de 98\% con un margen de error de 1 milla por galón, ¿cuántos automóviles deberán usarse? Suponga que por pruebas anteriores se sabe que la desviación estándar del rendimiento es 2.6 millas por galón.

Ejercicio 6.4 Obtener los dos intervalos de confianza unilaterales del 100(1-\alpha)\% para \theta, bajo el supuesto de que la varianza \sigma^2 es conocida.

6.1.2 Varianza desconocida

Ejercicio 6.5 Para una muestra aleatoria de una población Normal de media \mu = \theta y varianza \sigma^2 desconocida, demuestre que, \frac{\bar{X} - \theta}{S/\sqrt{n}} = \frac{\sqrt{n}(\bar{X} - \theta)}{S} es una variable pivote para \theta.

Ejercicio 6.6 A partir de la variable pivote del anterior ejercicio obtenga los respectivos intervalos de confianza bilateral de longitud mínima y unilaterales del 100(1-\alpha)\% para \theta.

¿Cuál sería la fórmula para el margen de error asociado al intervalo bilateral de longitud mínima?
¿Qué problema se presenta al tratar de obtener una fórmula para el tamaño de muestra asociado al intervalo bilateral de longitud mínima?

Ejercicio 6.7 (R. Walpole, R. Myers, S. Myers, K. Ye - Probabilidad y Estadística para Ingeniería y Ciencias. 9na Edición, Pearson (2012). Capítulo 9. Ejercicio 11.) Una máquina produce piezas metálicas de forma cilíndrica. Se toma una muestra de las piezas y los diámetros son 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 0.99, 1.01 y 1.03 centímetros.

¿Cuál es la estimación puntual de la media poblacional?
¿Cuál es la estimación puntual de la desviación estándar poblacional?
Con 95% de confianza, ¿cuál es el margen de error para la estimación de la media poblacional?
¿Cuál es el intervalo de confianza de 95% para la media poblacional?

6.2 Varianza

6.2.1 Media conocida

Para una muestra aleatoria de una población Normal de media \mu y varianza \sigma^2 = \theta, bajo el supuesto de que la media \mu es conocida, sabemos que, \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{\theta} \sim \chi^2_{n} es una variable pivote para \theta.

Ejercicio 6.8 A partir de la anterior variable pivote obtenga intervalos de confianza bilaterales del 100(1-\alpha)\% para la varianza \sigma^2 y para la desviación estándar \sigma.

Solución Ejercicio 6.8

Transformando la correspondiente variable pivote tenemos que, \begin{aligned} P \left[ a < \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{\theta} < b \right] &= 1 - \alpha \\ P \left[ \frac{1}{b} < \frac{\theta}{\sum_{i=1}^n \left(X_i - \mu\right)^2} < \frac{1}{a} \right] &= 1 - \alpha \\ P \left[ \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{b} < \theta < \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{a} \right] &= 1 - \alpha. \end{aligned}

Por lo tanto, \left( \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{b} , \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{a} \right) es un intervalo de confianza bilateral del 100(1-\alpha)\% para \theta, donde a y b serían cuantiles de la distribución chi-cuadrado con n grados de libertad, tales que \mathrm{F}_{\chi^2_n}(b) - \mathrm{F}_{\chi^2_n}(a) = 1 - \alpha, siendo \mathrm{F}_{\chi^2_n}(.) la función de distribución acumulativa chi-cuadrado con n grados de libertad.

Al variar los valores de a y b obtenemos infinitos intervalos de confianza del 100(1-\alpha)\% para \theta. Si se desea el intervalo de confianza de menor longitud posible entonces, \begin{aligned} \min_{a < b} \left\{ T^{(2)} - T^{(1)} \right\} &= \min_{a < b} \left\{ \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{a} - \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{b} \right\} \\ &= \min_{a < b} \left\{ \frac{1}{a} - \frac{1}{b} \right\} \end{aligned} es decir, minimizar la longitud del intervalo es equivalente a minimizar 1/a-1/b, con la condición o restricción de que \mathrm{F}_{\chi^2_n}(b) - \mathrm{F}_{\chi^2_n}(a) - 1 + \alpha = 0 (y de que a < b).

Derivando la función a minimizar con respecto a b, e igualando a cero se tiene que, \frac{\partial}{\partial b} \left( \frac{1}{a}-\frac{1}{b} \right) = - \frac{1}{a^2} \frac{\partial a}{\partial b} + \frac{1}{b^2} = 0, al derivar la restricción con respecto a b se tiene que, \begin{aligned} \frac{\partial}{\partial b} (\mathrm{F}_{\chi^2_n}(b) - \mathrm{F}_{\chi^2_n}(a) - 1 + \alpha) &= \frac{\partial}{\partial b} 0 \\ \mathrm{f}_{\chi^2_n}(b) - \mathrm{f}_{\chi^2_n}(a) \frac{\partial a}{\partial b} &= 0 \\ \frac{\partial a}{\partial b} &= \frac{\mathrm{f}_{\chi^2_n}(b)}{\mathrm{f}_{\chi^2_n}(a)} \end{aligned} y sustituyendo, \begin{aligned} - \frac{1}{a^2} \frac{\partial a}{\partial b} + \frac{1}{b^2} &= 0 \\ \frac{1}{b^2} &= \frac{1}{a^2} \frac{\mathrm{f}_{\chi^2_n}(b)}{\mathrm{f}_{\chi^2_n}(a)} \\ a^2 \, \mathrm{f}_{\chi^2_n}(a) &= b^2 \, \mathrm{f}_{\chi^2_n}(b) \\ 0 &= b^2 \, \mathrm{f}_{\chi^2_n}(b) - a^2 \, \mathrm{f}_{\chi^2_n}(a) \end{aligned} Dados los grados de libertad y el nivel de confianza, mediante métodos numéricos es posible encontrar los valores a y b que cumplen la anterior condición (requisito para longitud mínima). Sin embargo, por facilidad, usualmente se toma a = \chi^{2}_{(1-\alpha/2,n)} y b = \chi^{2}_{(\alpha/2,n)}, con la expectativa de que el impacto de usar esos valores sea pequeño en aquellos casos en que se tengan muestras grandes.

Código

# Encontrar los valores de a y b que cumplen las condiciones para obtener
# un intervalo de confianza de longitud mínima, dados n y el valor de alpha
n <- 50
alpha <- 0.05
### Función que se hace cero cuando se cumplen las condiciones
h <- function(a, v, level){
  b <- qchisq(level + pchisq(a, v), v) # Condición para nivel de confianza
  b^2 * dchisq(b, v) - a^2 * dchisq(a, v) # Condición para longitud mínima
}
### Encontrar valor de a que hace que la función h sea cero
ur <- uniroot(h, c(0 + 1e-8, qchisq(alpha, n) - 1e-8), tol = 1e-6,
              v = n, level = 1 - alpha)
a <- ur$root
b <- qchisq(1 - alpha + pchisq(a, n), n)
a.facil <- qchisq(alpha/2, n)
b.facil <- qchisq(1 - alpha/2, n)
round(rbind(solu.numerica=c(a = a, b = b, funcion.a.minim=1/a-1/b),
            por.facilidad=c(a.facil, b.facil, 1/a.facil-1/b.facil)), 4)

                    a       b funcion.a.minim
solu.numerica 33.8555 75.6958          0.0163
por.facilidad 32.3574 71.4202          0.0169

En conclusión, un intervalo de confianza bilateral del 100(1-\alpha)\% para \theta, bajo el supuesto de que la media \mu es conocida, y que además se puede obtener fácilmente con el uso de las tablas estadísticas es, \begin{aligned} &\left( \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{\chi^{2}_{(\alpha/2,n)}} , \frac{\sum_{i=1}^n \left(X_i - \mu\right)^2}{\chi^{2}_{(1-\alpha/2,n)}} \right) \\ &= \left( \frac{\sum_{i=1}^n X_i^2 - n \mu^2}{\chi^{2}_{(\alpha/2,n)}} , \frac{\sum_{i=1}^n X_i^2 - n \mu^2}{\chi^{2}_{(1-\alpha/2,n)}} \right) \end{aligned}

Un intervalo de confianza bilateral del 100(1-\alpha)\% para la desviación estándar \sigma = \sqrt{\theta}, bajo el supuesto de que la media \mu es conocida, y que además, se puede obtener fácilmente con el uso de las tablas estadísticas es, \left( \sqrt{\frac{\sum_{i=1}^n X_i^2 - n \mu^2}{\chi^{2}_{(\alpha/2,n)}}} , \sqrt{\frac{\sum_{i=1}^n X_i^2 - n \mu^2}{\chi^{2}_{(1-\alpha/2,n)}}} \right).

¿Qué condición se debe cumplir para que el intervalo de confianza bilateral de la desviación estándar sea de longitud mínima? ¿es la misma condición que se debe cumplir para que el intervalo de confianza bilateral de la varianza sea de longitud mínima?

Ejercicio 6.9 A partir de la variable pivote dada, obtenga los respectivos intervalos de confianza unilaterales del 100(1-\alpha)\% para la varianza \sigma^2 y para la desviación estándar \sigma.

6.2.2 Media desconocida

Para una muestra aleatoria de una población Normal de media \mu y varianza \theta, bajo el supuesto de que la media \mu es desconocida, \frac{(n-1)S^2}{\theta} \sim \chi^2_{n-1} es una variable pivote para \theta.

Ejercicio 6.10 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales del 100(1-\alpha)\% para \theta.

Ejercicio 6.11 (R. Walpole, R. Myers, S. Myers, K. Ye - Probabilidad y Estadística para Ingeniería y Ciencias. 9na Edición, Pearson (2012). Capítulo 9. Ejercicio 71.) Un fabricante de baterías para automóvil afirma que sus baterías durarán, en promedio, 3 años con una varianza de 1 año. Suponga que 5 de estas baterías tienen duraciones de 1.9, 2.4, 3.0, 3.5 y 4.2 años y con base en esto construya un intervalo de confianza del 95\% para la desviación estándar poblacional, después decida si es válida la afirmación del fabricante de que dicha desviación estándar poblacional es igual a 1. Suponga que la población de duraciones de las baterías se distribuye de forma aproximadamente normal.

6.3 Diferencia de medias

6.3.1 Muestras pareadas

Cuando las variables aleatorias X, Y representan variables medidas en las mismas unidades y que cuantifican el mismo aspecto de la unidad estadística sólo que en circunstancias distintas, y cuando D_i = X_i - Y_i tiene sentido, la muestra aleatoria (X_1,Y_1), (X_2,Y_2), \dots, (X_n,Y_n) se denomina muestra pareada o dependiente.

Sea D_1, \dots, D_n una muestra aleatoria de una población Normal de media \theta \left(\mu_D = \mu_X - \mu_Y = \theta\right) y varianza \sigma_D^2 \left(\sigma_D^2 = \sigma_X^2 + \sigma_Y^2 - 2 \rho \sigma_X \sigma_Y \right), bajo el supuesto de varianza desconocida, \frac{\sqrt{n}(\bar{D} - \theta)}{S_D} \sim t_{n-1} es una variable pivote para \theta.

Ejercicio 6.12 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales, de longitud mínima, del 100(1-\alpha)\% para \theta.

¿Cuál sería la fórmula para el margen de error asociado al intervalo bilateral?
¿Qué problema se presenta al tratar de obtener una fórmula para el tamaño de muestra asociado al intervalo bilateral?

Ejercicio 6.13 (D. Anderson, D. Sweeney, T. Williams, J. Camm - Estadística para Negocios y Economía. 11ra Edición, Cengage Learning (2012). Capítulo 10. Ejercicio 27.) Un fabricante produce dos modelos de una lijadora automática, uno de lujo y otro estándar, diseñado para uso doméstico. Los precios de venta de una muestra de distribuidores minoristas se presentan a continuación.

Minorista	1	2	3	4	5	6	7
Lujo	39	39	45	38	40	39	35
Estándar	27	28	35	30	30	34	29

¿Cuál es el intervalo de 95\% de confianza para la diferencia entre la media de los precios de ambos modelos?

6.3.2 Muestras independientes

6.3.2.1 Varianzas conocidas

Sean X_1, \dots, X_n y Y_1, \dots, Y_m muestras aleatorias independientes de poblaciones con distribución Normal de medias \mu_X y \mu_Y y varianzas conocidas \sigma_X^2 y \sigma_Y^2, respectivamente, \frac{ \left( \bar{X} - \bar{Y} \right) - \theta }{ \sqrt{\frac{\sigma_X^2}{n} + \frac{\sigma_Y^2}{m}} } \sim \mathcal{N}(0,1) es una variable pivote para \mu_X - \mu_Y = \theta.

Ejercicio 6.14 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales, de longitud mínima, del 100(1-\alpha)\% para \theta.

¿Cuál sería la fórmula para el margen de error asociado al intervalo bilateral?
¿Suponga que n = m y obtenga una fórmula para el tamaño de muestra n=m asociado al intervalo bilateral?

Ejercicio 6.15 (D. Anderson, D. Sweeney, T. Williams, J. Camm - Estadística para Negocios y Economía. 11ra Edición, Cengage Learning (2012). Capítulo 10. Ejercicio 5.) Se esperaba que el Día de San Valentín el gasto promedio fuera de \$100.89 (USA Today, 13 de febrero de 2006). ¿Hay diferencia en las cantidades que desembolsan los hombres y las mujeres? El gasto promedio en una muestra de 40 hombres fue de \$135.67 y en una muestra de 30 mujeres fue de \$68.64. Por estudios anteriores se sabe que la desviación estándar poblacional en el consumo de los hombres es \$35 y en el de las mujeres es \$20.

¿Cuál es la estimación puntual de la diferencia entre el gasto medio poblacional de los hombres y el gasto medio poblacional de las mujeres?
Con 99\% de confianza, ¿cuál es el margen de error?
Elabore un intervalo de confianza de 99\% para la diferencia entre las dos medias poblacionales.

6.3.2.2 Varianzas desconocidas, suponiendo igualdad

Sean X_1, \dots, X_n y Y_1, \dots, Y_m muestras aleatorias independientes de poblaciones con distribución Normal de medias \mu_X y \mu_Y, respectivamente, y varianzas desconocidas pero iguales \sigma_X^2 = \sigma_Y^2, \frac{ \left( \bar{X} - \bar{Y} \right) - \theta }{ S_p \, \sqrt{\frac{1}{n}+\frac{1}{m}}} \sim t_{n+m-2}, con S_p = \sqrt{ \frac{(n-1)S_X^2 + (m-1)S_Y^2}{n+m-2} }, es una variable pivote para \mu_X - \mu_Y = \theta.

Ejercicio 6.16 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales, de longitud mínima, del 100(1-\alpha)\% para \theta.

¿Cuál sería la fórmula para el margen de error asociado al intervalo bilateral?

Ejercicio 6.17 (R. Walpole, R. Myers, S. Myers, K. Ye - Probabilidad y Estadística para Ingeniería y Ciencias. 9na Edición, Pearson (2012). Capítulo 9. Ejercicio 46.) Los siguientes datos representan el tiempo de duración de películas producidas por dos empresas cinematográficas.

Empresa
I	103	94	110	87	98
II	97	82	123	92	175	88	118

Calcule un intervalo de confianza del 90\% para la diferencia entre la duración promedio de las películas que producen las dos empresas. Suponga que las diferencias en la duración se distribuyen de forma aproximadamente normal y que tienen varianzas iguales.

6.3.2.3 Varianzas desconocidas, sin suponer igualdad

Sean X_1, \dots, X_n y Y_1, \dots, Y_m muestras aleatorias independientes de poblaciones con distribución Normal de medias \mu_X y \mu_Y y varianzas desconocidas y distintas \sigma_X^2 y \sigma_Y^2, respectivamente, \frac{ \left( \bar{X} - \bar{Y} \right) - \theta }{ \sqrt{\frac{S_X^2}{n}+\frac{S_Y^2}{m}}} \sim t_{v}, con v \approx \frac{\left( s^2_X / n + s^2_Y / m \right)^2}{ \frac{\left(s^2_X / n\right)^2}{n-1} + \frac{\left(s^2_Y / m\right)^2}{m-1} }, es una variable pivote para \mu_X - \mu_Y = \theta.

Ejercicio 6.18 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales, de longitud mínima, del 100(1-\alpha)\% para \theta.

¿Cuál sería la fórmula para el margen de error asociado al intervalo bilateral?

Ejercicio 6.19 (R. Walpole, R. Myers, S. Myers, K. Ye - Probabilidad y Estadística para Ingeniería y Ciencias. 9na Edición, Pearson (2012). Capítulo 9. Ejercicio 46.) Los siguientes datos representan el tiempo de duración de películas producidas por dos empresas cinematográficas.

Empresa
I	103	94	110	87	98
II	97	82	123	92	175	88	118

6.4 Cociente de varianzas

6.4.1 Muestras independientes

6.4.1.1 Medias conocidas

Para X_1, \dots, X_n y Y_1, \dots, Y_m muestras aleatorias independientes de poblaciones con distribución Normal de medias conocidas \mu_X y \mu_Y y varianzas \sigma_X^2 y \sigma_Y^2, respectivamente, \frac{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m}{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n} \theta \sim F_{m, n} es una variable pivote para \sigma_X^2 / \sigma^2_Y = \left( \sigma_X / \sigma_Y \right)^2 = \theta.

Ejercicio 6.20 A partir de la anterior variable pivote obtenga un intervalo de confianza bilateral del 100(1-\alpha)\% para el cociente de varianzas \theta.

Solución Ejercicio 6.20

Transformando la correspondiente variable pivote tenemos que, \begin{aligned} P \left[ a < \frac{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m}{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n} \theta < b \right] &= 1 - \alpha \\ P \left[ a \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} < \theta < b \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} \right] &= 1 - \alpha \end{aligned}

Por lo tanto, \left( a \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m}, b \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} \right) es un intervalo de confianza bilateral del 100(1-\alpha)\% para \theta, donde a y b serían cuantiles de la distribución F con m y n grados de libertad, tales que \mathrm{F}_{F_{m,n}}(b) - \mathrm{F}_{F_{m,n}}(a) = 1- \alpha, siendo \mathrm{F}_{F_{m,n}}(.) la función de distribución acumulativa F de Fisher con m y n grados de libertad.

Al variar los valores de a y b obtenemos infinitos intervalos de confianza del 100(1-\alpha)\% para \theta. Si se desea el intervalo de confianza de menor longitud posible, entonces, \begin{aligned} \min_{a < b} \left\{ T^{(2)} - T^{(1)} \right\} &= \min_{a < b} \left\{ b \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} - a \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} \right\} \\ &= \min_{a < b} \left\{ b - a \right\} \end{aligned} es decir, minimizar la longitud del intervalo es equivalente a minimizar b-a, con la condición o restricción de que \mathrm{F}_{F_{m,n}}(b) - \mathrm{F}_{F_{m,n}}(a) - 1 + \alpha = 0 (y de que a < b).

De manera similar a lo realizado con los intervalos de confianza para la media suponiendo la varianza conocida, se llega a la conclusión de que la longitud del intervalo es mínima cuando \mathrm{f}_{F_{m,n}}(a) = \mathrm{f}_{F_{m,n}}(b). Dados los grados de libertad y el nivel de confianza, mediante métodos numéricos es posible encontrar los valores a y b que cumplen la anterior condición (requisito para longitud mínima). Nuevamente, por facilidad se toma a = f_{(1-\alpha/2, m, n)} y b = f_{(\alpha/2, m, n)}, con la expectativa de que el impacto de usar esos valores sea pequeño para aquellos casos en que tengamos muestras grandes.

Código

# Encontrar los valores de a y b que cumplen las condiciones para obtener
# un intervalo de confianza de longitud mínima, dados n, m y el valor de alpha
n <- 50; m <- 60; alpha <- 0.10
### Función que se hace cero cuando se cumplen las condiciones
h <- function(a, v1, v2, level){
  b <- qf(level + pf(a, v1, v2), v1, v2) # Condición para nivel de confianza
  df(b, v1, v2) - df(a, v1, v2) # Condición para longitud mínima
}
### Encontrar valor de a que hace que la función h sea cero
ur <- uniroot(h, c(0 + 1e-8, qf(alpha, m, n) - 1e-8), tol = 1e-6,
              v1 = m, v2 = n, level = 1 - alpha)
a <- ur$root
b <- qf(1 - alpha + pf(a, m, n), m, n)
### Gráfico 
f.a <- df(a, m, n); f.b <- df(b, m, n)
curve(df(x, m, n), 0, 3, bty="n", ylab = expression(f(x)))
abline(h = f.a, col = "orange"); abline(h = f.b, col = "orange")
x <- seq(a, b, 0.01); y <- df(x, m, n)
polygon(c(b,b,a,a,x), c(f.b,0,0,f.a,y), col = "orange")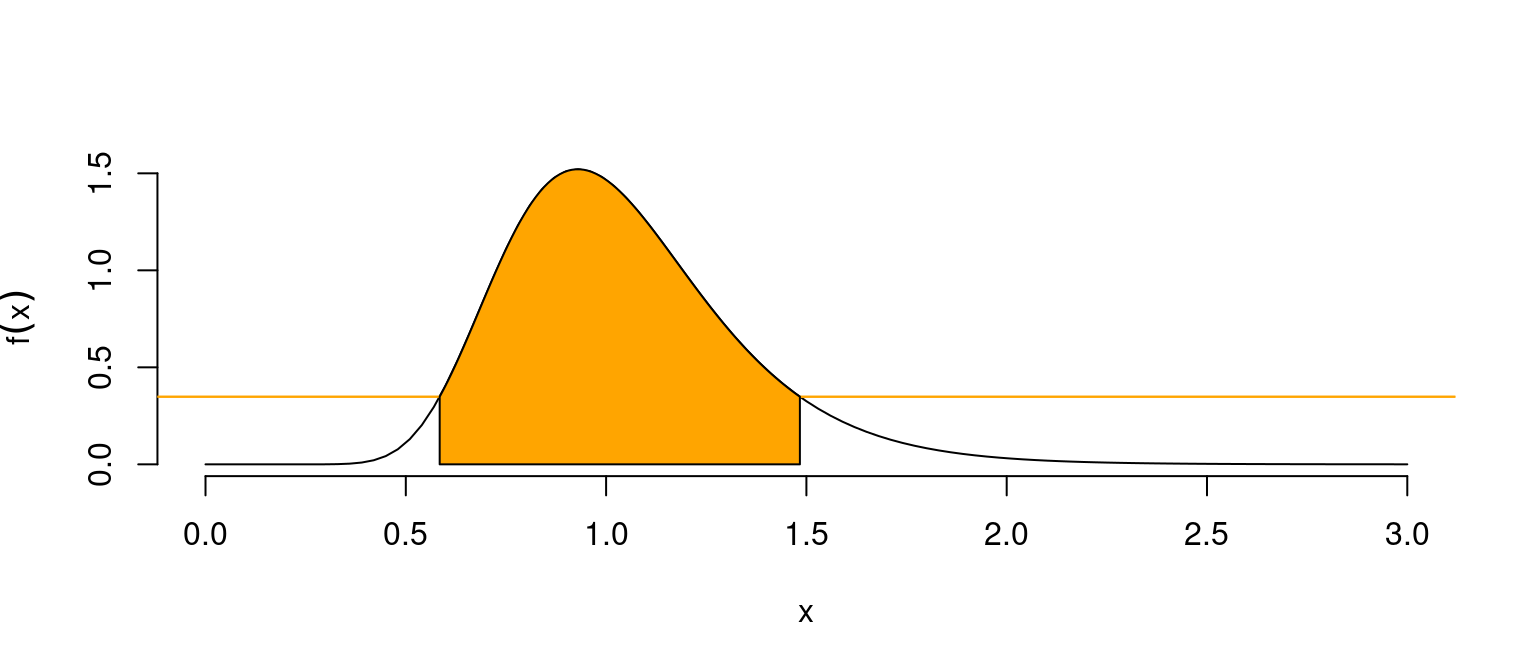

Código

a.facil <- qf(alpha/2, m, n) # Por facilidad
b.facil <- qf(1 - alpha/2, m, n) # Por facilidad
round(rbind(solu.numerica=c(a = a, b = b, funcion.a.minim=b-a),
            por.facilidad=c(a.facil, b.facil, b.facil-a.facil)), 4)

                   a      b funcion.a.minim
solu.numerica 0.5846 1.4838          0.8992
por.facilidad 0.6414 1.5757          0.9342

En conclusión, un intervalo de confianza bilateral del 100(1-\alpha)\% para \sigma_X^2 / \sigma^2_Y = \theta, a partir de muestras de dos poblaciones independientes con medias conocidas, y que además se puede obtener con el uso de las tablas estadísticas, es, \begin{aligned} & \left( f_{(1-\alpha/2, m, n)} \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m}, f_{(\alpha/2, m, n)} \frac{\sum_{i=1}^{n} \left( X_i - \mu_X \right)^2 / n}{\sum_{i=1}^{m} \left( Y_i - \mu_Y \right)^2 / m} \right) \\ & = \left( f_{(1-\alpha/2, m, n)} \frac{\frac{1}{n} \sum_{i=1}^{n} X_i^2 - \mu_X^2}{\frac{1}{m} \sum_{i=1}^{m} Y_i^2 - \mu_Y^2}, f_{(\alpha/2, m, n)} \frac{\frac{1}{n} \sum_{i=1}^{n} X_i^2 - \mu_X^2}{\frac{1}{m} \sum_{i=1}^{m} Y_i^2 - \mu_Y^2} \right) \\ & = \left( \frac{1}{f_{(\alpha/2, n, m)}} \frac{\frac{1}{n} \sum_{i=1}^{n} X_i^2 - \mu_X^2}{\frac{1}{m} \sum_{i=1}^{m} Y_i^2 - \mu_Y^2}, f_{(\alpha/2, m, n)} \frac{\frac{1}{n} \sum_{i=1}^{n} X_i^2 - \mu_X^2}{\frac{1}{m} \sum_{i=1}^{m} Y_i^2 - \mu_Y^2} \right) \end{aligned}

Ejercicio 6.21 A partir de la variable pivote dada, obtenga los respectivos intervalos de confianza unilaterales de 100(1-\alpha)\% para el cociente de varianzas \theta.

6.4.1.2 Medias desconocidas

Sean X_1, \dots, X_n y Y_1, \dots, Y_m muestras aleatorias independientes de poblaciones con distribución Normal de medias desconocidas \mu_X y \mu_Y y varianzas \sigma_X^2 y \sigma_Y^2, respectivamente. \frac{\sum_{i=1}^{m} \left( Y_i - \bar{Y} \right)^2 / (m-1)}{\sum_{i=1}^{n} \left( X_i - \bar{X} \right)^2 / (n-1)} \theta = \frac{S_Y^2}{S_X^2} \theta \sim F_{m-1, n-1} es una variable pivote para \sigma_X^2 / \sigma^2_Y = \left( \sigma_X / \sigma_Y \right)^2 = \theta.

Ejercicio 6.22 A partir de la anterior variable pivote obtenga los respectivos intervalos de confianza bilateral y unilaterales del 100(1-\alpha)\% para el cociente de varianzas \sigma_X^2 / \sigma^2_Y.

¿Cuáles serían los intervalos de confianza bilateral y unilaterales del 100(1-\alpha)\% para el cociente de desviaciones estándar \sigma_X / \sigma_Y?

Ejercicio 6.23 (R. Walpole, R. Myers, S. Myers, K. Ye - Probabilidad y Estadística para Ingeniería y Ciencias. 9na Edición, Pearson (2012). Capítulo 9. Ejercicio 79.) Construya un intervalo de confianza del 90\% para \sigma_1 / \sigma_2 en el Ejercicio 6.19.

¿De acuerdo al intervalo de confianza resultante, al construir un intervalo de confianza para la diferencia de medias, lo correcto sería suponer que las varianzas / desviaciones estándar poblacionales son iguales o que no lo son?