EN CONSTRUCCION.
En esta sección se hará una revisión de la transformación inversa de probabilidad y del método de la transformada inversa para la generación de valores aleatorios.
Teorema 1 (Inverse transform sampling) Sea U una variable aleatoria uniforme continua en el intervalo [0,1] \left(U \sim \mathcal{U}(0,1)\right), F(\cdot) una función de distribución acumulativa y F^{-}(u) = \inf \left\{ x : u \leq F(x) \right\} para 0 < u < 1, entonces la variable aleatoria X = F^{-}(U) tiene como función de distribución acumulativa F(\cdot).
Prueba. Como F es continua a derecha, por ser función de distribución acumulativa, entonces \left\{ x : u \leq F(x) \right\} = \left\{ x : F^{-}(u) \leq x \right\}. Además, como U \sim \mathcal{U}(0,1), entonces, F_U(u) = u para 0 \leq u < 1. Por lo tanto, \begin{aligned} F_X(x) &= P[X \leq x] \\ &= P\big[F^{-}(U) \leq x\big] \\ &= P\big[U \leq F(x)\big] \\ &= F_U \big( F(x) \big) \\ &= F(x) \end{aligned} De donde se concluye que la variable aleatoria X = F^{-}(U) tiene como función de distribución acumulativa F(\cdot).
Ejercicio 1 Sea F(x;\beta) = 1 - \exp\left(-\frac{x}{\beta}\right) para x > 0.
F(\cdot) cumple todas las condiciones de una función de distribución acumulativa.
Gráfico de la función F(x; \beta):
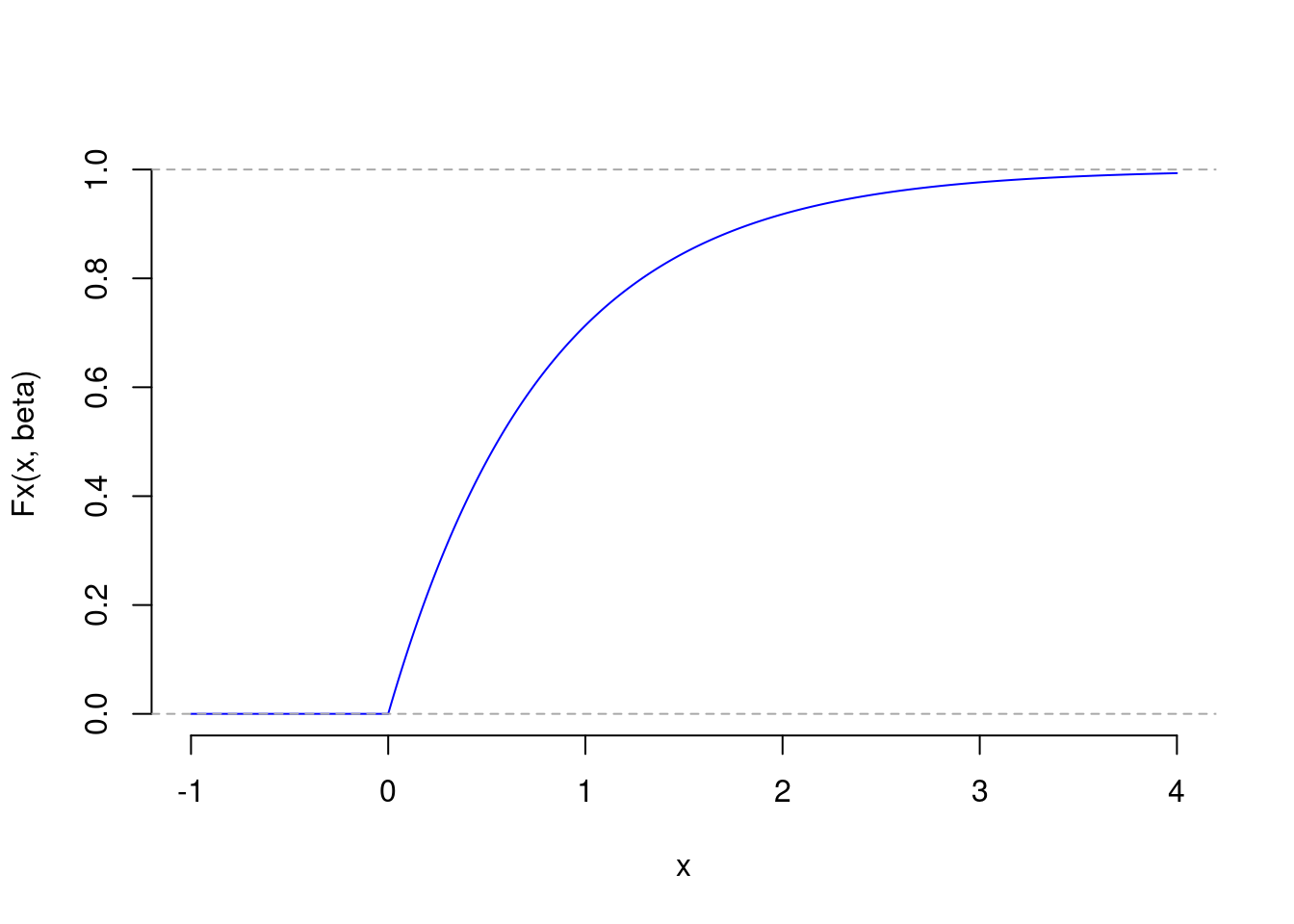
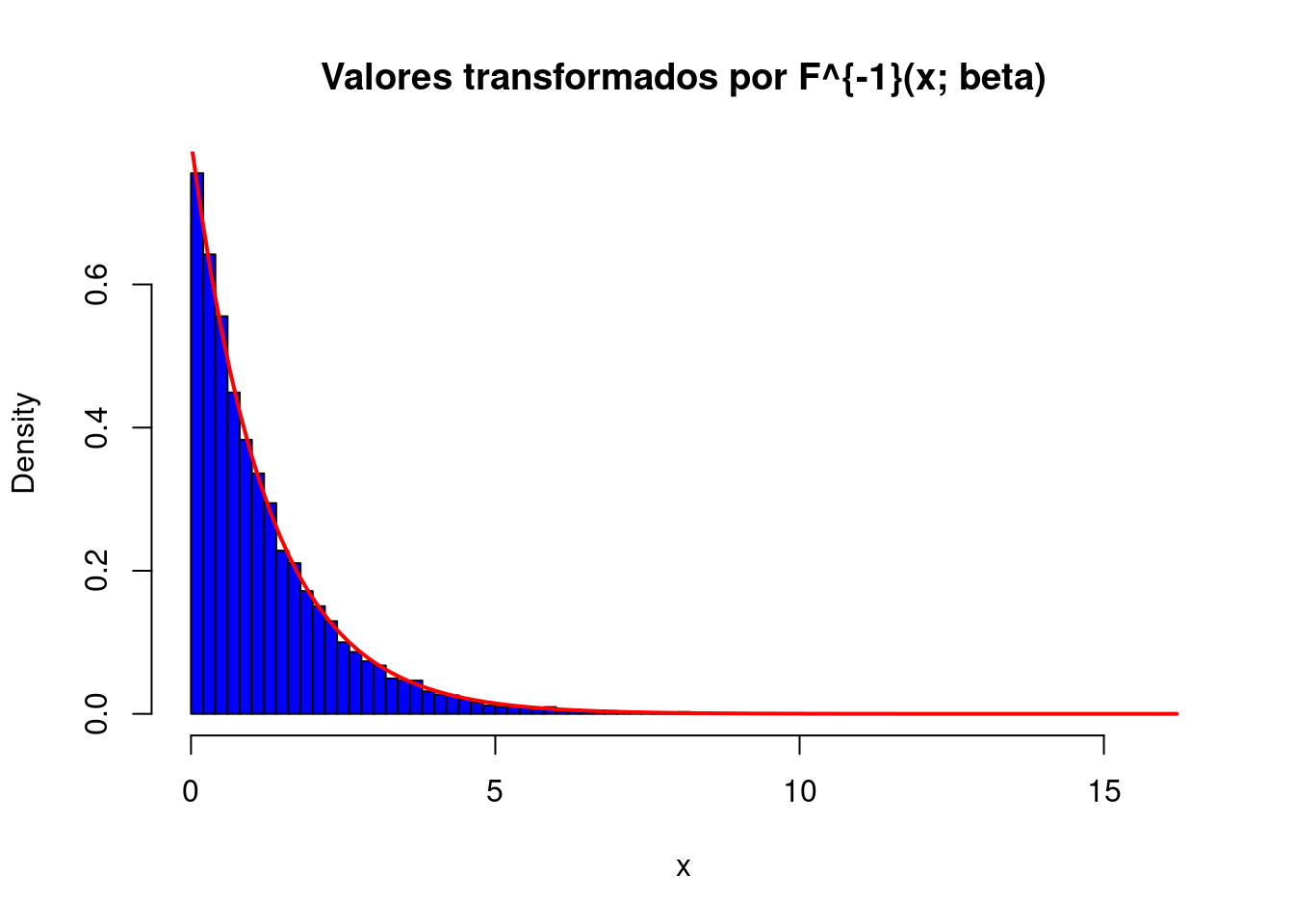
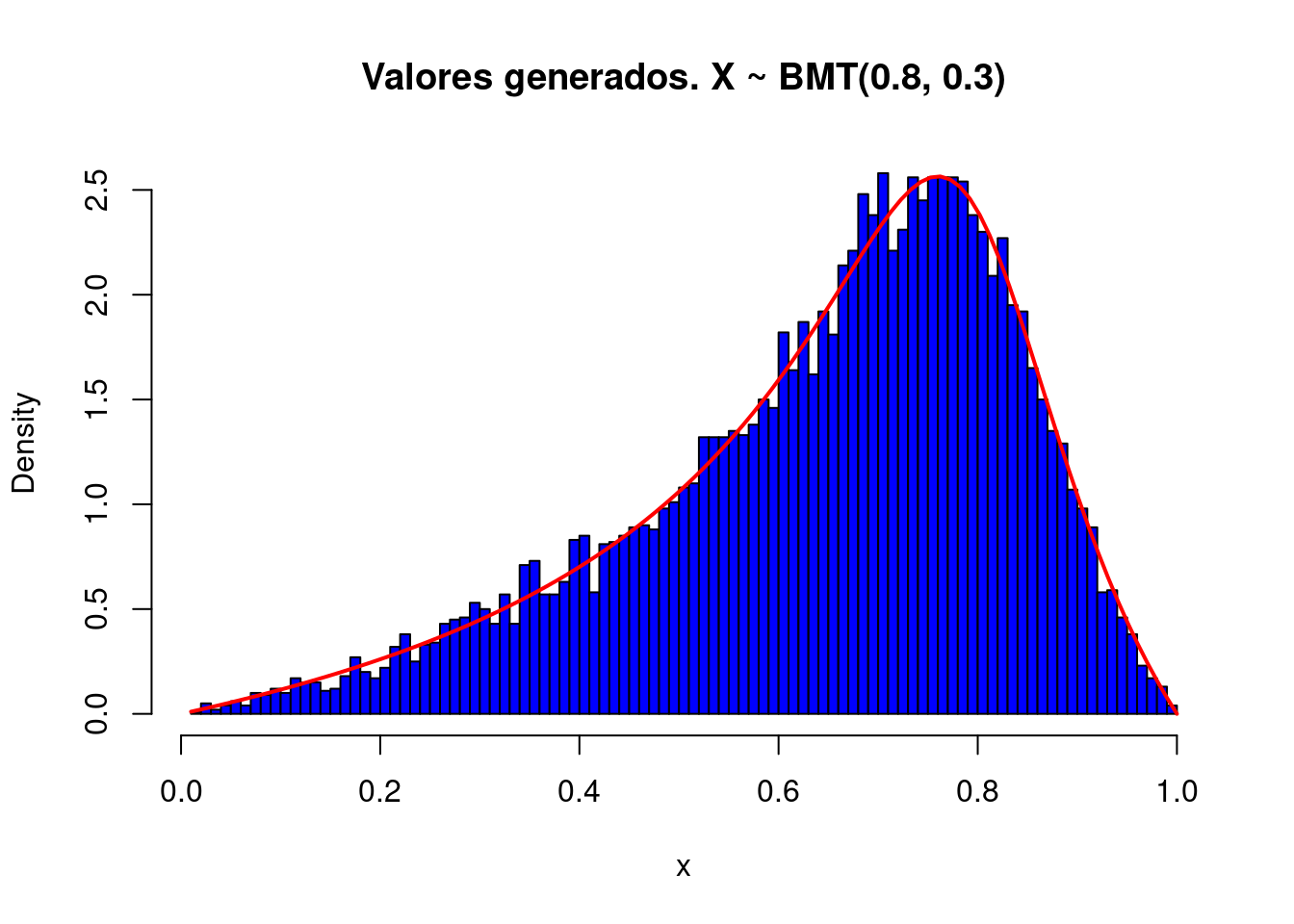
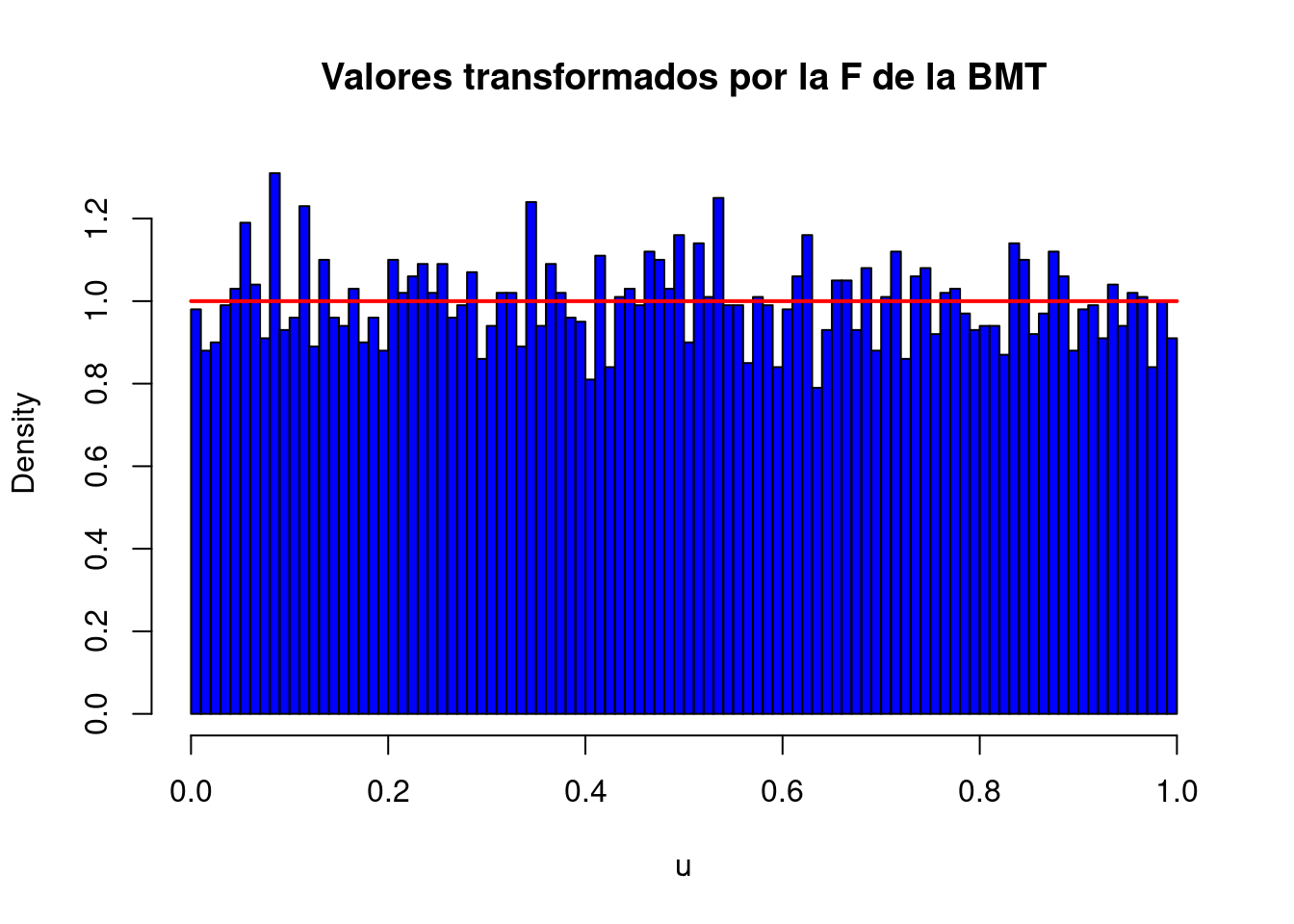
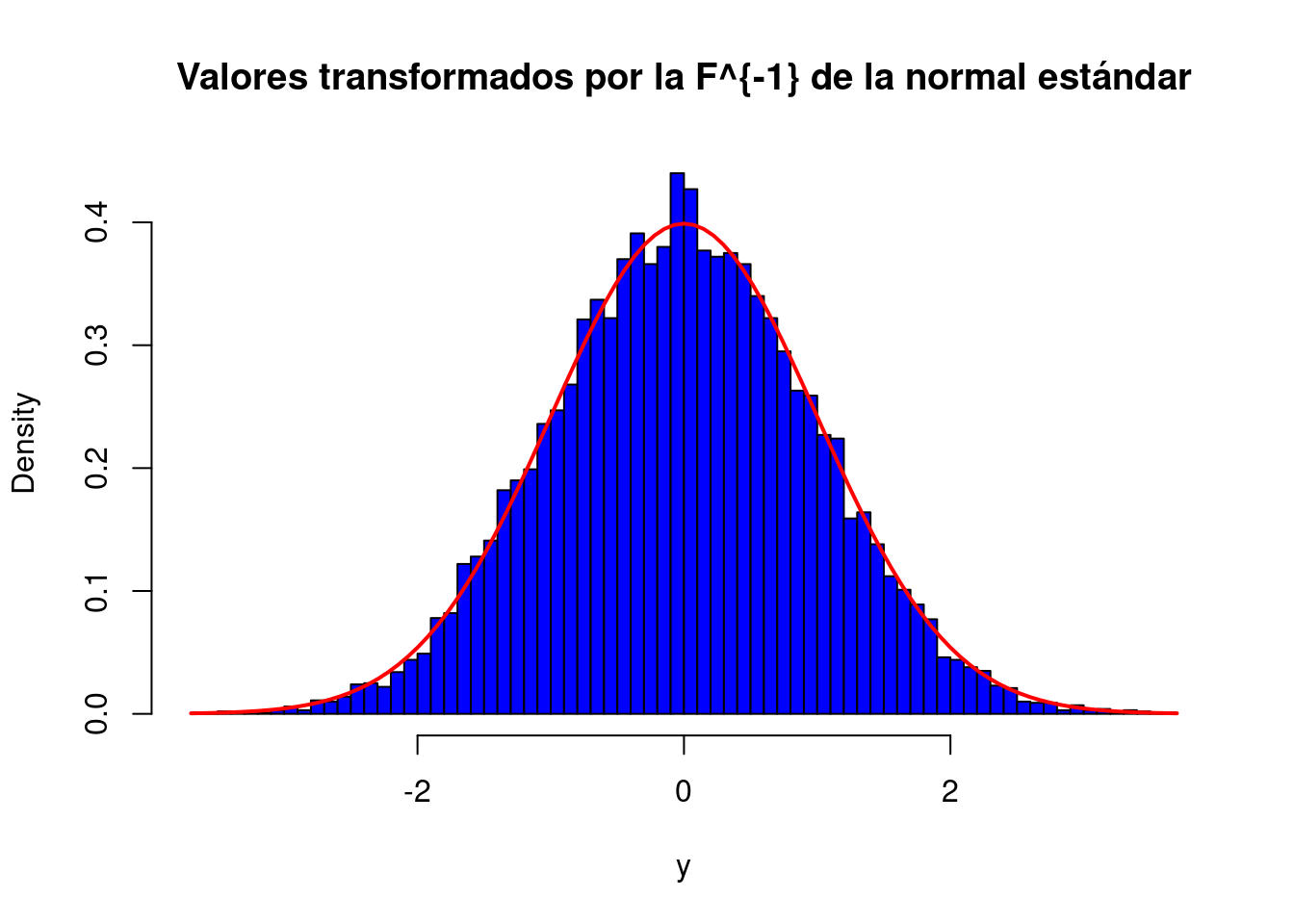
# Parámetro beta:
beta <- 0.8
# Función F(x; beta):
Fx <- function(x, beta){
res <- 1 - exp(-x/beta)
ifelse(x > 0, res, 0)
}
# Grafica de la función F(x: beta):
curve(Fx(x, beta), from=-1, to=4, n=1e4, bty="n", col="blue")
# Grafica líneas horizontales y = 0 y y = 1:
abline(h=c(0,1), lty=2, col="darkgrey") 
Para 0 < u < 1, \begin{aligned} F(x) &= u \\ 1 - \exp\left(-\frac{x}{\beta}\right) &= u \\ \exp\left(-\frac{x}{\beta}\right) &= 1 - u \\ -\frac{x}{\beta} &= \log \left( 1 - u \right) \\ x &= - \beta \log \left( 1 - u \right) \\ x &= F^{-1}(u) \end{aligned}
¿Cuál sería la distribución de la variable aleatoria \begin{aligned} X &= F^{-1}(U;\beta) \\ &= - \beta \log \left( 1 - U \right), \end{aligned} para U \sim \mathcal{U}(0,1)?
El resultado del Teorema 1 se puede utilizar para generar valores pseudoaleatorios de una distribución para la cual podamos obtener x = F^{-}(u).
x será un valor pseudoaleatorio proveniente de una variable aleatoria con función de distribución acumulativa F(\cdot).
Ejemplo 1 ¿Qué pasa si generamos una cierta cantidad de valores pseudoaleatorios de una distribución uniforme en (0,1) y luego les aplicamos la función F^{-1}(U;\beta) = - \beta \log \left( 1 - u \right)?
Generación de valores pseudoaleatorios de una distribución uniforme:
# Establecer semilla
set.seed(2023)
# Número de valores a generar:
n <- 1e4
# Generar pseudoaleatorios para una distribución uniforme:
u <- runif(n)
# Histograma de los valores generados:
hist(u, freq=FALSE, col="blue", breaks = sqrt(n),
main="Valores generados. X ~ U(0,1)")
# Grafica función de densidad uniforme (0,1)
lines(c(0,1), c(1,1), col="red", lwd=2)
Aplicamos la función F^{-1}(U;\beta) = - \beta \log \left( 1 - u \right):
# Parámetro beta:
beta <- 1.25
# Función F^{-1}(x; beta):
FInvu <- function(u, beta){
res <- - beta * log(1 - u)
ifelse(u > 0 | u < 1, res, 0)
}
# Transformar los valores mediante la función F^{-1}(x; beta):
x <- FInvu(u, beta)
# Histograma de los valores transformados por la función:
hist(x, freq=FALSE, col="blue", breaks = sqrt(n),
main="Valores transformados por F^{-1}(x; beta)")
# Grafica de la función f(x; beta) = exp(-x / beta) / beta
curve(exp(-x / beta) / beta, add=TRUE, col="red", lwd=2)
¿Cuál es la distribución de la variable aleatoria correspondiente a los valores que se obtuvieron al final?
Teorema 2 (Probability integral transform) Sea X una variable aleatoria con función de distribución acumulativa continua y creciente F_X(\cdot), entonces la variable aleatoria U = F_X(X) tiene distribución uniforme continua sobre el intervalo [0,1].
Prueba. Sea Y = F_X(X), entonces, para 0 \leq y < 1, \begin{aligned} F_Y(y) &= P[Y \leq y] \\ &= P\big[F_X(X) \leq y\big] \\ &= P\big[X \leq F^{-1}_X(y)\big] \\ &= F_X \left( F^{-1}_X(y) \right) \\ &= y \\ \end{aligned} Por lo tanto, Y \sim \mathcal{U}(0,1).
Supongamos que tengo unos valores observados provenientes de una variable aleatoria con cierta distribución, ¿qué transformación sería la adecuada para llevarlos a que sean valores observados de una variable aleatorio con cierta distribución de mi preferencia?
Ejemplo 2 Supongamos que tengo unos valores observados provenientes de una variable aleatoria con distribución BMT y supongamos que quiero transformarlos adecuadamente para que lleguen a una distribución normal estándar.
Supongamos que tenemos valores de una distribución BMT:
# Instalar y cargar la libreria de la distribución BMT
if(!require(BMT)) { install.packages("BMT"); require(BMT) }
library(BMT)
# Número de valores a generar:
n <- 1e4
# Valores para los parámetros de la BMT
kappa_l <- 0.8; kappa_r <- 0.3
# Generar pseudoaleatorios para una distribución uniforme:
x <- rBMT(n, kappa_l, kappa_r)
# Histograma de los valores generados:
hist(x, freq=FALSE, col="blue", breaks = sqrt(n),
main=paste0("Valores generados. X ~ BMT(",
kappa_l, ", ", kappa_r, ")"))
# Grafica función de densidad BMT
curve(dBMT(x, kappa_l, kappa_r), add = TRUE, col = "red", lwd=2)
Valores transformados por la función de distribución acumulativa BMT:
# Transformar los valores mediante la función F de la BMT:
u <- pBMT(x, kappa_l, kappa_r)
# Histograma de los valores transformados por la F de la BMT:
hist(u, freq=FALSE, col="blue", breaks = sqrt(n),
main="Valores transformados por la F de la BMT")
# Grafica función de densidad uniforme (0,1)
lines(c(0,1), c(1,1), col="red", lwd=2)
Valores transformados por la función cuantil de la normal estándar:
# Transformar los valores mediante la función F^{-1} de la normal estándar:
y <- qnorm(u)
# Histograma de los valores transformados por la F de la BMT:
hist(y, freq=FALSE, col="blue", breaks = sqrt(n),
main="Valores transformados por la F^{-1} de la normal estándar")
# Grafica función de densidad normal estándar
curve(dnorm(x), add = TRUE, col = "red", lwd=2)
Partimos de unos datos distribuidos BMT y al transformarlos adecuadamente llegamos a datos con distribución normal estándar.
En el anterior ejemplo (con datos), solamente fue necesario el poder computar la F(\cdot) de la BMT y la F^{-1}(\cdot) de la normal; no fue necesario que dichas funciones tuviesen expresiones analíticas cerradas. Si tenemos expresiones analíticas cerradas para las funciones de distribución acumulativas involucradas y para sus inversas entonces tendremos una expresión analítica cerrada para transformar la respectiva variable aleatoria inicial, a la variable con distribución deseada, tanto de ida como de regreso.
EN CONSTRUCCION.