Variables aleatorias

EN CONSTRUCCION.

En esta sección se hará una revisión de algunos temas relacionados con variables aleatorias como lo son: la medida de probabilidad asociada a una variable aleatoria, las funciones de distribución acumulativas, las funciones de masa de probabilidad y de densidad, el valor esperado, la varianza, la desigualdad de Chebyshev y los cuantiles de una variable aleatoria.

Recordemos, ¿qué objeto matemático es una medida de probabilidad P[\cdot]?

Tip

\begin{aligned} P : \wp (\Omega) &\longrightarrow [0,1] \\ A &\longrightarrow P[A] = p \\ \\ A \subseteq \Omega &\qquad 0 \leq p \leq 1 \end{aligned}

Definición

Sea X una variable asociada al “Número de puntos en la cara superior de un dado común de seis caras luego de lanzarlo una vez” o equivalentemente al “Resultado al lanzar, una vez, un dado común y corriente de seis caras”.

Evidentemente, los valores que puede llegar a tomar X son x = 1, 2, 3, 4, 5, 6. Además, se puede ver que la “variable” X resulta ser el objeto matemático representado por el siguiente gráfico:

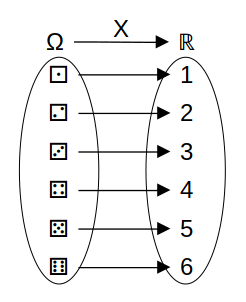
Definición 1 (Variable aleatoria) Una variable aleatoria es una función que asigna un número real a cada uno de los elementos del espacio muestral.

\begin{aligned} X : \Omega &\longrightarrow \mathbb{R} \\ \omega &\longrightarrow X(w) = x \in \mathbb{R} \end{aligned}

En otras palabras, una variable aleatoria es una representación o asociación numérica (en los números reales) para los resultados de un experimento aleatorio.

Ejercicio 1 Asocie una variable aleatoria a los siguientes experimentos aleatorios:

• Sacar una carta de un mazo (baraja).
• Resultado de un partido (“ganar”, “perder”, “empatar”).

Medida de probabilidad asociada

Es lógico querer una manera de obtener probabilidades para un conjunto B de potenciales valores x en los reales, que podría tomar la variable aleatoria X. Es decir quisiera una medida de probabilidad P_X tal que:

\begin{aligned} P_X : \mathcal{B} (\mathbb{R}) &\longrightarrow [0,1] \\ B &\longrightarrow P_X[B] = p \in [0,1] \end{aligned}

¿Cómo podríamos usar lo que ya hemos visto para lograr lo que queremos o necesitamos?

Ya tenemos una X y una P tal que,

Además, recordemos que,

• Imagen: Sea A \subset \Omega, la imagen de A por X es X(A) = \{x \in \mathbb{R}: X(\omega) = x \text{, para algún } \omega \in A\}

• Preimagen: Sea B \subset \mathbb{R}, la preimagen de B por X es X^{-1}(B) = \{\omega \in \Omega: x = X(\omega) \text{, para algún } x \in B\}

Entonces, se puede definir la probabilidad de que la variable aleatoria X tome un subconjunto de valores en los reales B de la siguiente manera:

\begin{aligned} P_X[B] &= P_X[\{ x: x \in B \}] \\ &= P[\{ \omega \in \Omega: X(w) = x \text{, para algún } x \in B \}] \\ &= P[X^{-1}(B)] \end{aligned}

Es decir, obtenemos P_X haciendo la composición de X^{-1} y P.

Además, P_X cumple todos los axiomas, y por ende todas las propiedades, de una medida de probabilidad. Lo único que cambia con respecto a lo anteriormente visto acerca de probabilidades es que siempre estaremos trabajando con conjuntos en los números reales, en vez de estar trabajando con conjuntos de espacios muestrales distintos que dependen del experimento aleatorio.

Abusando un poco de la notación, siempre utilizaremos P[X \in B] para referirnos a P_X[B].

Lo cual implica que,

• Si B = \{a\} entonces \begin{aligned} P_X\big[\{a\}\big] &= P\Big[X^{-1}\big(\{a\}\big)\Big] \\ &= P\big[X \in \{a\}\big] \\ &= P[X=a] \end{aligned}

• Si B = (a,b] entonces \begin{aligned} P_X\big[(a,b]\big] &= P\Big[X^{-1}\big((a,b]\big)\Big] \\ &= P\big[X \in (a,b]\big] \\ &= P[a < X \leq b] \end{aligned}

En los siguientes ejercicios, reescriba la probabilidad solicitada en términos de la variable aleatoria usando la notación indicada, y si es posible obtenga el valor para dicha probabilidad.

Ejercicio 2 Sea X := “Número que aparece en la cara superior de un dado después de ser lanzado una vez”.

P[\text{``Sacar más de 4''}] = \text{¿?}

Ejercicio 3 Sea Y := “El resultado de un partido codificado de la siguiente manera: Ganar=1, Empatar=0, Perder=-1”.

P[\text{``No perder''}] = \text{¿?}

Ejercicio 4 Sea Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.

P[\text{``Sacar al menos dos sellos''}] = \text{¿?}

Función de distribución acumulativa

La función de distribución acumulativa F_X de una variable aleatoria X se define como: \begin{aligned}F_X(x) &:= P \big[ X \in (-\infty,x] \big] \\&= P[ X \leq x ]\end{aligned} donde x \in \mathbb{R}.

Para que una función (F_X) sea una función de distribución acumulativa, de una variable aleatoria X, debe cumplir lo siguiente:

1. F_X es no decreciente (Si x_1 \leq x_2 entonces F_X(x_1) \leq F_X(x_2)).
2. F_X es continua a derecha \left( F_X(x^+) = \lim\limits_{h \to 0} F_X(x + h) = F_X(x) \right).
3. F_X tiende a cero cuando x tiende a menos infinito \left( \lim\limits_{x \to -\infty} F_X(x) = 0 \right).
4. F_X tiende a uno cuando x tiende a infinito \left(\lim\limits_{x \to \infty} F_X(x) = 1\right).

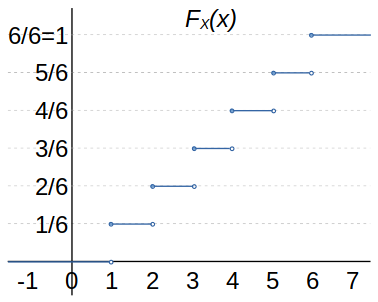
Ejercicio 5 Determine y haga el gráfico de la función de distribución acumulativa asociada a la siguiente variable aleatoria:

X := “Resultado al lanzar, una vez, un dado común y corriente”.

Solución

Valores que toma la variable aleatoria X:

x = 1, 2, 3, 4, 5, 6.

La función de distribución acumulativa asociada a la variable aleatoria X es,

F_X(x) = \begin{cases} \frac{0}{6}=0 & \text{si } x < 1 \\ \frac{1}{6} & \text{si } 1 \leq x < 2 \\ \frac{2}{6} & \text{si } 2 \leq x < 3 \\ \frac{3}{6} & \text{si } 3 \leq x < 4 \\ \frac{4}{6} & \text{si } 4 \leq x < 5 \\ \frac{5}{6} & \text{si } 5 \leq x < 6 \\ \frac{6}{6}=1 & \text{si } 6 \leq x \end{cases}

y su gráfico sería,

¿Cómo hallar cualquier probabilidad deseada, a partir de la función de distribución acumulativa?

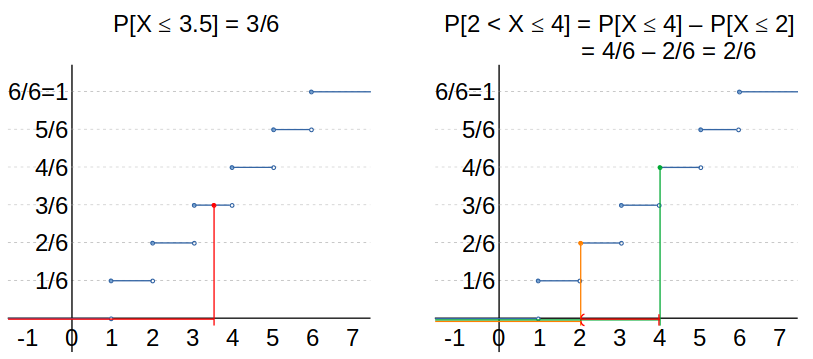
Si se conoce la función de distribución acumulativa de una variable aleatoria, entonces,

\begin{aligned} P[X \leq b] &= F_X(b) \\ \\ P[X < b] &= \lim\limits_{h \to 0} F_X(b-h) \\&= F_X(b^-) \\ \\ P[a < X \leq b] &= P[X \leq b] - P[X \leq a] \\&= F_X(b) - F_X(a) \\ \\ P[a \leq X < b] &= P[X < b] - P[X < a] \\&= F_X(b^-) - F_X(a^-) \\ \\ P[a < X < b] &= P[X < b] - P[X \leq a] \\&= F_X(b^-) - F_X(a) \\ \\ P[a \leq X \leq b] &= P[X \leq b] - P[X < a] \\&= F_X(b) - F_X(a^-) \\ \\ P[X = a] &= P[a \leq X \leq a] \\&= P[X \leq a] - P[X < a] \\&= F_X(a) - F_X(a^-) \end{aligned}

Las variables aleatorias se clasifican en:

• Discretas: Cuando F_X es una función escalonada. (X(\Omega) es un conjunto finito o numerable)

• Continuas: Cuando F_X es una función continua. (X(\Omega) es un intervalo o unión de intervalos)

• Mixtas: Cuando F_X es una combinación de al menos una función de distribución acumulativa escalonada y una función de distribución acumulativa continua.

Ejercicio 6 Determine y haga el gráfico de la función de distribución acumulativa asociada a la siguiente variable aleatoria:

Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.

Solución

Valores que toma la variable aleatoria Z:

z = 0, 1, 2, 3.

F_Z(z) = \begin{cases} \frac{0}{8} = 0 & \text{si } z < 0 \\ \frac{1}{8} & \text{si } 0 \leq z < 1 \\ \frac{4}{8} & \text{si } 1 \leq z < 2 \\ \frac{7}{8} & \text{si } 2 \leq z < 3 \\ \frac{8}{8} = 1 & \text{si } 3 \leq z \end{cases}

Función de masa de probabilidad y función de densidad

Función de masa de probabilidad

La función de masa de probabilidad f_X de una variable aleatoria discreta X se define como: \begin{aligned}f_X(x) &:= F_X(x) - F_X(x^-) \\&= P[X=x]\end{aligned} donde x \in \mathbb{R}.

Para que una función (f_X) sea una función de masa de probabilidad, de una variable aleatoria discreta X, debe cumplir lo siguiente:

1. f_X(x) \geq 0, para todo x \in \mathbb{R}.
2. \sum\limits_{t \in \mathbb{R}} f_X(t) = 1.

Ejercicio 7 Determine y haga el gráfico de la función de masa de probabilidad asociada a la siguiente variable aleatoria:

X := “Resultado al lanzar, una vez, un dado común y corriente”.

Solución

Valores que toma la variable aleatoria X:

x = 1, 2, 3, 4, 5, 6.

x	1	2	3	4	5	6
f_X(x) = P[X=x]	\frac{1}{6}	\frac{1}{6}	\frac{1}{6}	\frac{1}{6}	\frac{1}{6}	\frac{1}{6}

¿Cómo hallar cualquier probabilidad deseada, a partir de la función de masa de probabilidad?

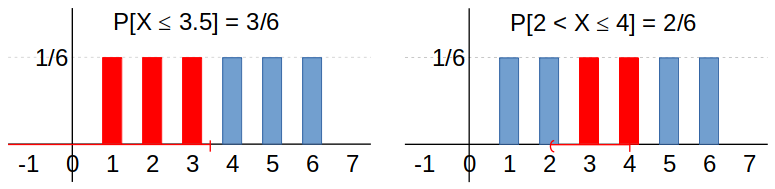
Si se conoce la función de masa de probabilidad de una variable aleatoria, entonces,

\begin{aligned} P[X \in B] &= \sum\limits_{t \in B} f_X(t) \\ \\ P[a < X \leq b] &= \sum\limits_{a < t \leq b} f_X(t) \\ \\ P[a \leq X < b] &= \sum\limits_{a \leq t < b} f_X(t) \\ \\ \vdots \end{aligned}

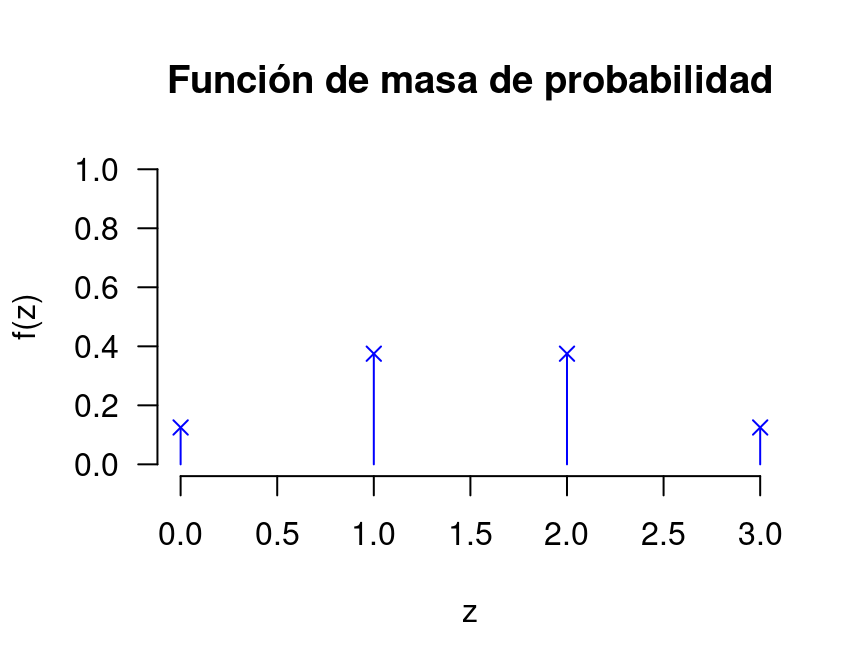
Ejercicio 8 Determine y haga el gráfico de la función de masa de probabilidad asociada a la siguiente variable aleatoria:

Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.

Solución

Valores que toma la variable aleatoria Z:

z = 0, 1, 2, 3.

x	0	1	2	3
f_X(x) = P[X=x]	\frac{1}{8}	\frac{3}{8}	\frac{3}{8}	\frac{1}{8}

Función de densidad

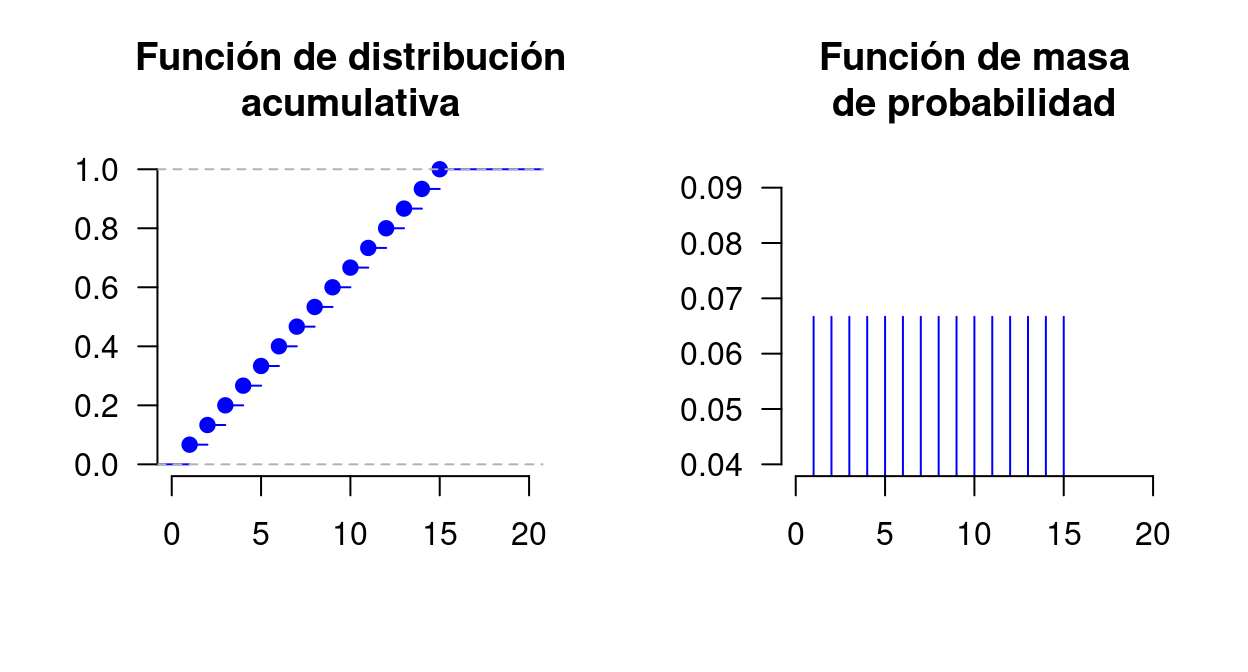
Sea una variable aleatoria X definida como “el tiempo que se debe esperar para…”.

Supongamos que una persona erronea o incorrectamente dice que dicha variable aleatoria es discreta con valores x = 1, 2, \dots, 15 minutos, todos ellos igualmente probables, entonces,

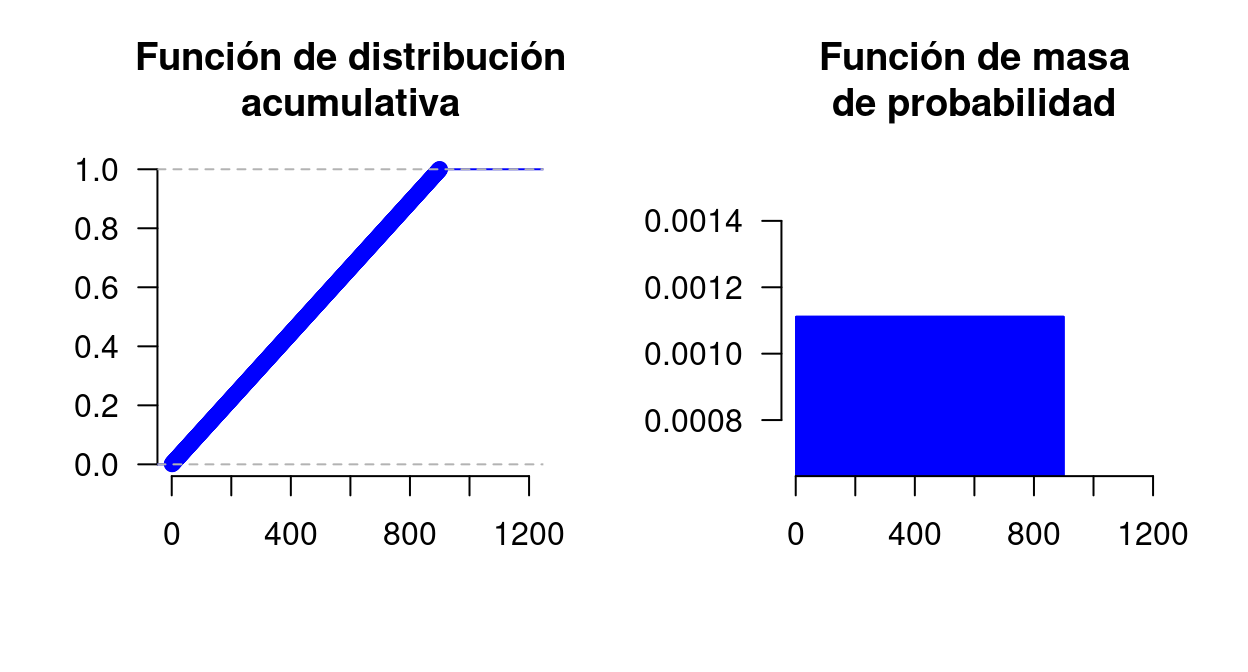
Ahora, supongamos que esa persona empieza a darse cuenta que algo anda mal e intenta corregir su error pasando de minutos a segundos, de donde asume erronea o incorrectamente que la variable aleatoria es discreta con valores x = 1, 2, \dots, 900 segundos, todos ellos igualmente probables, entonces,

Finalmente la persona se da cuenta de que el error que está cometiendo consiste en considerar como discreta una variable que es continua (desde la parte de estadística descriptiva hemos evidenciado que una variable relacionada con el tiempo es cuantitativa continua con escala de medida de razón). Sin embargo, gracias al error cometido podemos imaginar lo que ocurrirá cuando el tiempo se divida en partes cada vez más pequeñas, hasta llegar a unidades de tiempo infinitesimales. Cuando el tiempo que debo esperar varía infinitesimalmente entre 0 y 15 minutos (0 < x < 15) con igual probabilidad, entonces,

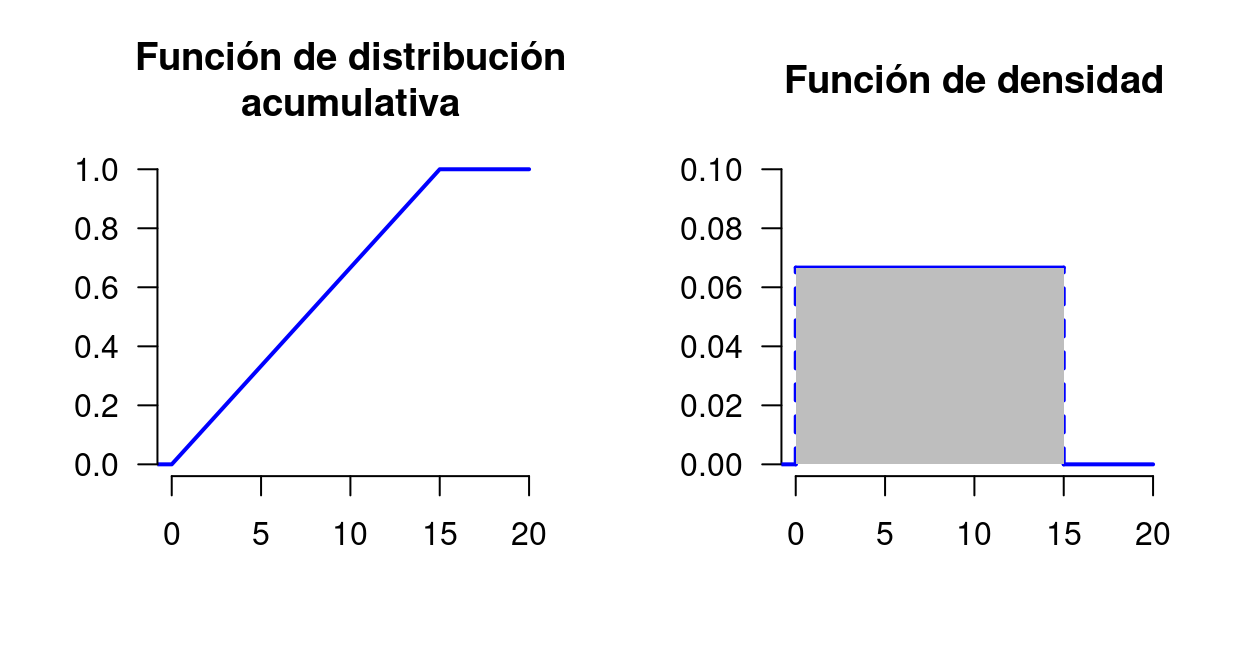
Si para una variable aleatoria discreta se tiene que f_X(x) := F_X(x) - F_X(x^-), entonces ¿cual sería la fórmula equivalente (infinitesimal) para una aleatoria continua?

La función de densidad f_X de una variable aleatoria continua X se define como: \begin{aligned}f_X(x) &:= \lim_{h \to 0} \frac{F_X(x + h) - F_X(x)}{(x + h) - x} \\ &=\frac{d}{dx} F_X(x) \\ &= F'_X (x)\end{aligned}

Una función f_X es función de densidad de una variable aleatoria continua X si:

1. f_X(x) \geq 0, para todo x \in \mathbb{R}.
2. \int\limits_{t \in \mathbb{R}} f_X(t) \, dt = \int\limits_{-\infty}^{\infty} f_X(t) \, dt = 1

Note que,

\begin{aligned}F_X(x) &= P[X \leq x] \\ &= \int\limits_{-\infty}^x f_X(t) \, dt\end{aligned}

Es decir que P[X \leq x] es igual al área acumulada bajo la curva y = f_X(t) desde -\infty hasta el valor dado para x.

Ejercicio 9  

La vida útil, en días, para frascos de cierta medicina de prescripción es una variable aleatoria que tiene la siguiente función de densidad:

f_X(x) = \begin{cases} \frac{20000}{(x+100)^3} & x > 0 \\ 0 & \text{en otro caso} \end{cases}

Calcule la probabilidad de que un frasco de esta medicina tenga una vida útil de: (a) al menos 200 días; (b) cualquier lapso entre 80 y 120 días.

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 3.6.

Si se conoce la función de densidad de una variable aleatoria, entonces,

\begin{aligned} P[X \in B] &= \int\limits_{t \in B} f_X(t) dt \\ \\ P[a \leq X \leq b] &= \int\limits_{a \leq t \leq b} f_X(t) dt \\&= \int\limits_{a}^{b} f_X(t) dt \end{aligned}

Es decir que P[a \leq X \leq b] es igual al área bajo la curva dada por f_X(t), entre las rectas x=a y x=b.

Si X una variable aleatoria continua, entonces P[X=a] = ¿?.

A partir de todo lo visto en las anteriores secciones, concluimos que basta con conocer la función de distribución acumulativa o la función de densidad (la función de masa de probabilidad para el caso discreto) para conocer por completo el mecanismo aleatorio que rige a la variable aleatoria y al experimento aleatorio respectivo (y por ende, se puede calcular cualquier probabilidad que se quiera).

Cuantiles

El cuantil x_p, para p \in [0,1], de una variable aleatoria X es un valor que toma la variable tal que: P[X \leq x_p] \geq p \qquad \text{ y } \qquad P[X \geq x_p] \geq 1-p

Un cuantil x_q no es necesariamente único. Cuando un cuantil no es único, existe un intervalo en el que cada punto del intervalo satisface las dos condiciones para ser cuantil.

Ejercicio 10 Encuentre los cuartiles 1, 2, y 3 (cuantiles 0.25, 0.5 y 0.75) del número de caras que aparecen en el lanzamiento tres veces consecutivas de una moneda común y corriente.

Tip

Z := “El número de caras que aparecen en el lanzamiento tres veces consecutivas de una moneda común y corriente”.

Valores que toma la variable: z = 0, 1, 2, 3.

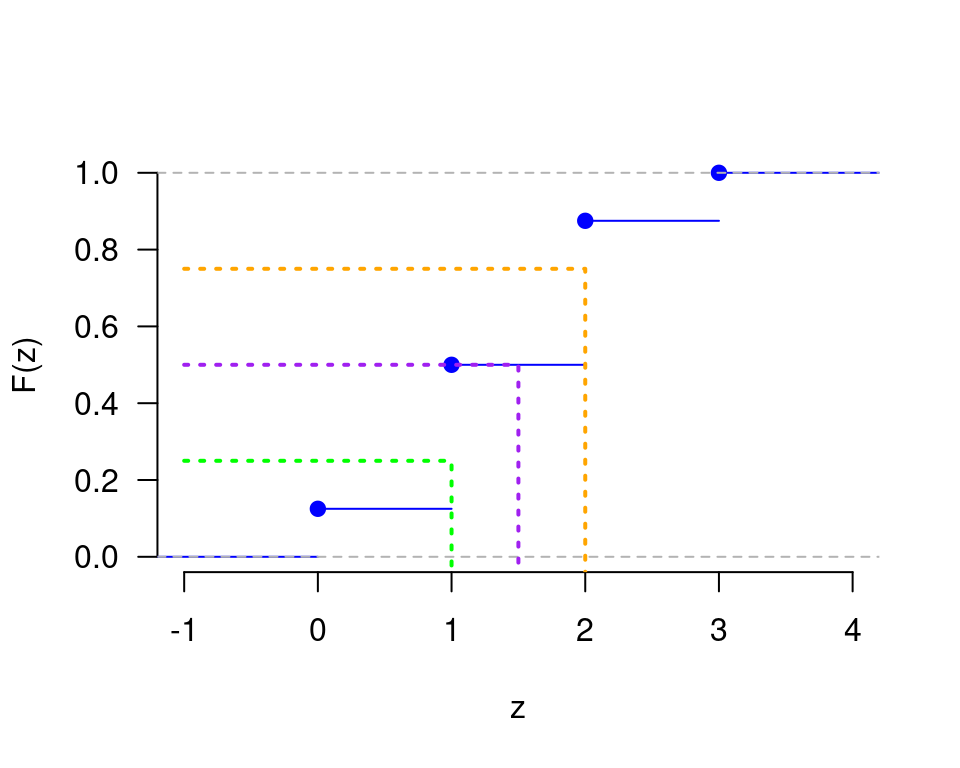
Note que para una variable aleatoria continua X, se tiene que, \begin{aligned} P[X \leq x_p] &= p \\ F_X[x_p] &= p \\ x_p &= F_X^{-1}(p) \end{aligned}

Una función inversa de la función de distribución acumulativa de la variable aleatoria X se denomina función cuantil de X.

Ejercicios

A continuación se encuentran una serie de ejercicios tomados del siguiente libro:

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación.

Ejercicio 11 (Walpole 3.1)  

Clasifique las siguientes variables aleatorias como discretas o continuas:

X: el número de accidentes automovilísticos que ocurren al año en Virginia.

Y: el tiempo para jugar 18 hoyos de golf.

M: la cantidad de leche que una vaca específica produce anualmente.

N: el número de huevos que una gallina pone mensualmente.

P: el número de permisos para construcción que los funcionarios de una ciudad emiten cada mes.

Q: el peso del grano producido por acre.

Ejercicio 12 (Walpole 3.3)  

Sea W la variable aleatoria que da el número de caras menos el número de cruces en tres lanzamientos de una moneda. Liste los elementos del espacio muestral S para los tres lanzamientos de la moneda y asigne un valor w de W a cada punto muestral.

Ejercicio 13 (Walpole 3.5)  

Determine el valor c de modo que cada una de las siguientes funciones sirva como distribución de probabilidad de la variable aleatoria discreta X:

1. c \left( x^2 + 4 \right), para x = 0, 1, 2, 3;

2. c \binom{2}{x} \binom{3}{3 - x}, para x = 0, 1, 2.

Ejercicio 14 (Walpole 3.7)  

El número total de horas, medidas en unidades de 100 horas, que una familia utiliza una aspiradora en un periodo de un año es una variable aleatoria continua X que tiene la siguiente función de densidad: f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Calcule la probabilidad de que en un periodo de un año una familia utilice su aspiradora,

1. menos de 120 horas;

2. entre 50 y 100 horas.

Ejercicio 15 (Walpole 3.13)  

La distribución de probabilidad de X, el número de imperfecciones que se encuentran en cada 10 metros de una tela sintética que viene en rollos continuos de ancho uniforme, está dada por

x	0	1	2	3	4
f(x)	0.41	0.37	0.16	0.05	0.01

Construya la función de distribución acumulativa de X.

Valor esperado o esperanza

El valor esperado / la esperanza / el promedio para una variable aleatoria discreta X es: \begin{aligned} \mu_X &= E[X] \\ &= \sum_{t \in \mathbb{R}} t \, f_X(t) \\ &= \sum_{t \in \mathbb{R}} t \, P[X=t] \end{aligned}

El valor esperado / la esperanza / el promedio para una variable aleatoria continua X es: \begin{aligned} \mu_X &= E[X] \\ &= \int_{t \in \mathbb{R}} t \, f_X(t) \, dt \\ &= \int_{-\infty}^{\infty} t \, f_X(t) \, dt \end{aligned}

Propiedades del valor esperado:

• Si X=a constante, entonces E[X] = E[a] = a.
• E[X + b] = E[X] + b.
• E[a \, X] = a \, E[X].

Ejercicio 16 Encuentre el valor esperado / la esperanza / el promedio del número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente.

Solución

Z := “El número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente”.

Valores que toma la variable: z = 0, 1, 2, 3.

\begin{aligned} E[Z] &= \sum_{t \in \mathbb{R}} t \, f_Z(t) = \sum_{t \in \mathbb{R}} t \, P[Z=t] \\ &= \sum_{z=0}^3 z \, f_Z(z) = \sum_{z=0}^3 z \, P[Z=z] \\ &= (0) \, P[Z=0] + (1) \, P[Z=1] + (2) \, P[Z=2] + (3) \, P[Z=3] \\ &= (0) \, \frac{1}{8} + (1) \, \frac{3}{8} + (2) \, \frac{3}{8} + (3) \, \frac{1}{8} \\ &= \frac{3}{8} + \frac{6}{8} + \frac{3}{8} \\ &= \frac{12}{8} \\ &= 1.5 \end{aligned}

Ejercicio 17 Encuentre el valor esperado / la esperanza / el promedio del número de puntos que aparecen en la cara superior de un dado común y corriente de seis caras que se lanza una vez.

Solución

X := “Resultado al lanzar, una vez, un dado común y corriente”.

Valores que toma la variable: x = 1, 2, 3, 4, 5, 6.

x	f_X(x)	x \, f_X(x)
1	\frac{1}{6}	\frac{1}{6}
2	\frac{1}{6}	\frac{2}{6}
3	\frac{1}{6}	\frac{3}{6}
4	\frac{1}{6}	\frac{4}{6}
5	\frac{1}{6}	\frac{5}{6}
6	\frac{1}{6}	\frac{6}{6}
\,	Suma:	\sum\limits_{x=0}^3 x \, f_X(x) = \frac{21}{6} = 3.5

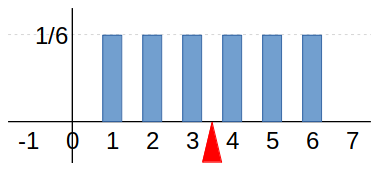
Ejercicio 18 Suponga que en un juego de azar inicialmente se debe apostar \$ 10 000 pesos, luego se lanza un dado común y corriente de seis caras y por cada punto que salga en la cara superior del dado, el apostador recibe \$ 2 500. ¿A la larga, cuál será la ganancia-perdida promedio de el(los) apostador(es) por cada vez que se apueste?

Solución

Si X := “Resultado al lanzar, una vez, un dado común y corriente”, entonces Y = \$ 2500 X - \$ 10000 sería la variable aleatoria asociada a la ganancia-perdida de el(los) apostador(es).

x	f_X(x)	y	f_Y(y)	y \, f_Y(y)
1	\frac{1}{6}	-7500	\frac{1}{6}	\frac{-7500}{6}
2	\frac{1}{6}	-5000	\frac{1}{6}	\frac{-5000}{6}
3	\frac{1}{6}	-2500	\frac{1}{6}	\frac{-2500}{6}
4	\frac{1}{6}	0	\frac{1}{6}	\frac{0}{6}
5	\frac{1}{6}	2500	\frac{1}{6}	\frac{2500}{6}
6	\frac{1}{6}	5000	\frac{1}{6}	\frac{5000}{6}
\,	\,	\,	Suma:	\sum\limits_{i=1}^{6} y_i \, f_Y(y_i) = \frac{-7500}{6} = -1250

Si hubiese tenido en cuenta las propiedades del valor esperado: \begin{aligned} E[Y] &= E[2500 X - 10000] \\ &= 2500 E[X] - 10000 \\ &= 2500 (3.5) - 10000 \\ &= -1250 \end{aligned} Es decir que, a la larga y en promedio, el(los) apostador(es) perderán \$ 1 250 pesos por cada vez que se apueste.

Valor esperado de una función

El valor esperado de una función g(X) de una variable aleatoria discreta X es: \begin{aligned} \mu_{g(X)} &= E[g(X)] \\ &= \sum_{t \in \mathbb{R}} g(t) \, f_X(t) \\ &= \sum_{t \in \mathbb{R}} g(t) \, P[X=t] \end{aligned}

El valor esperado de una función g(X) de una variable aleatoria continua X es: \begin{aligned} \mu_{g(X)} &= E[g(X)] \\ &= \int_{t \in \mathbb{R}} g(t) \, f_X(t) \, dt \\ &= \int_{-\infty}^{\infty} g(t) \, f_X(t) \, dt \end{aligned}

Ejercicio 19 Encuentre la ganancia-perdida promedio de un apostador, si de entrada tiene que apostar \$ 500, y si gana \$ 100 por el número al cuadrado de caras que aparecen en el lanzamiento de una moneda normal tres veces.

Solución

Sea Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”. La función de ganancia-perdida sería g(Z) = 100 \, Z^2 - 500.

\begin{aligned} E[100 \, Z^2 - 500] &= \sum_{t \in \mathbb{R}} \left(100 \, t^2 - 500\right) \, P[Z=t] \\ &= \sum_{z=0}^3 \left(100 \, z^2 - 500\right) \, P[Z=z] \\ &= (-500) \, \frac{1}{8} + (-400) \, \frac{3}{8} + (-100) \, \frac{3}{8} + (400) \, \frac{1}{8} \\ &= (-500) \, \frac{1}{8} + (-1200) \, \frac{1}{8} + (-300) \, \frac{1}{8} + (400) \, \frac{1}{8} \\ &= (-1600)\, \frac{1}{8} \\ &= -200 \end{aligned}

Ejercicio 20 Si inicialmente se debe apostar \$ 7500 pesos, y se gana el resultado de un dado común elevado al cubo y multiplicado por \$ 100. ¿A la larga, cuál será la ganancia-perdida promedio de un apostador por cada vez que apueste?

Solución

Sea X := “Resultado al lanzar, una vez, un dado común y corriente”. Y = g(X) = 100 X^3 - 7500 sería la variable aleatoria asociada a la ganancia-perdida.

Además, \begin{aligned} E[Y] &= E\left[100 X^3 - 7500\right] \\ &= 100 E\left[X^3\right] - 7500. \end{aligned}

x	f_X(x)	g(x)=x^3	g(x) \, f_X(x)
1	\frac{1}{6}	1	\frac{1}{6}
2	\frac{1}{6}	8	\frac{8}{6}
3	\frac{1}{6}	27	\frac{27}{6}
4	\frac{1}{6}	64	\frac{64}{6}
5	\frac{1}{6}	125	\frac{125}{6}
6	\frac{1}{6}	216	\frac{216}{6}
\,	\,	Suma:	\sum\limits_{x=1}^6 g(x) \, f_X(x) = \frac{441}{6} = 73.5

\begin{aligned} E[Y] &= 100 E\left[X^3\right] - 7500 \\ &= 100 (73.5) - 7500 \\ &= -150 \end{aligned}

Es decir que por cada vez que se apueste, a la larga en promedio se perderán \$ 150.

Varianza

La varianza de una variable aleatoria X es: \begin{aligned} \sigma_X^2 &= Var[X] \\ &= E \Big[ \big( X - E[X] \big)^2 \Big] \\ &= E\big[X^2\big] - \big(E[X]\big)^2 \end{aligned}

Propiedades de la varianza:

• Var[X] \geq 0, para toda variable aleatoria X.
• Si X=a constante, entonces Var[X] = Var[a] = 0.
• Var[X + b] = Var[X].
• Var[a \, X] = a^2 \, Var[X].

Ejercicio 21 Encuentre la varianza del número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente.

Solución

Z := “El número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente”.

Valores que toma la variable: z = 0, 1, 2, 3.

\begin{aligned} Var[Z] &= E\left[Z^2\right] - \left(E[Z]\right)^2 \\ &= \left(\sum_{z=0}^3 z^2 \, P[Z=z]\right) - (1.5)^2 \\ &= (0) \, \frac{1}{8} + (1) \, \frac{3}{8} + (4) \, \frac{3}{8} + (9) \, \frac{1}{8} - (1.5)^2 \\ &= \frac{3}{8} + \frac{12}{8} + \frac{9}{8} - (1.5)^2 \\ &= \frac{24}{8} - (1.5)^2 \\ &= 3 - (1.5)^2 \\ &= 0.75 \end{aligned}

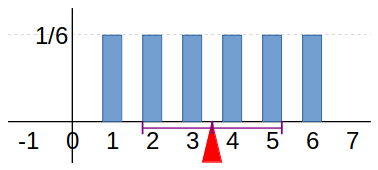
Ejercicio 22 Encuentre la varianza y la desviación estándar del número de puntos que aparecen en la cara superior de un dado común y corriente de seis caras que se lanza una vez.

Solución

X := “Resultado al lanzar, una vez, un dado común y corriente”.

Valores que toma la variable: x = 1, 2, 3, 4, 5, 6.

x	f_X(x)	x^2 \, f_X(x)
1	\frac{1}{6}	\frac{1}{6}
2	\frac{1}{6}	\frac{4}{6}
3	\frac{1}{6}	\frac{9}{6}
4	\frac{1}{6}	\frac{16}{6}
5	\frac{1}{6}	\frac{25}{6}
6	\frac{1}{6}	\frac{36}{6}
\,	Suma:	\sum\limits_{x=1}^{6} x^2 \, f_X(x) = \frac{91}{6} = 15.1666\bar{6}

Var[X] = 15.1666\bar{6} - (3.5)^2 = 2.9166\bar{6}

SD[X] = \sqrt{2.9166\bar{6}} = 1.707825

Desigualdad de Chebyshev

Para toda variable aleatoria X (denotando \mu_X = E[X] y \sigma^2_X = Var[X]), la probabilidad de que ésta tome valores a k desviaciones estándar de la media es por lo menos (es como mínimo) 1 - \frac{1}{k^2}. Es decir, \begin{aligned} P\big[\mu_X - (k) \, \sigma_X < X < \mu_X + (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ P\big[- (k) \, \sigma_X < X - \mu_X < (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ P\big[ |X - \mu_X| < (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \end{aligned} para k dado.

Por ejemplo, para k = 1 se concluye que, \begin{aligned} P\big[ |X - \mu_X| < (1) \, \sigma_X\big] &\geq 1 - \frac{1}{(1)^2} \\ P\big[ |X - \mu_X| < \sigma_X\big] &\geq 0 \\ P\big[\mu_X - \sigma_X < X < \mu_X + \sigma_X\big] &\geq 0 \end{aligned} para toda variable aleatoria X. Conclusión que es obvia, ya que toda probabilidad es mayor que cero. Sin embargo, para k > 1 tendríamos conclusiones más interesantes. Por ejemplo, para k = 2.5 se concluye que, \begin{aligned} P\big[ |X - \mu_X| < (2.5) \, \sigma_X\big] &\geq 1 - \frac{1}{(2.5)^2} \\ P\big[\mu_X - (2.5) \, \sigma_X < X < \mu_X + (2.5) \, \sigma_X\big] &\geq 0.84 \end{aligned} para toda variable aleatoria X (sin importar su distribución).

Por otro lado, si en \begin{aligned} P\big[\mu_X - (k) \, \sigma_X < X < \mu_X + (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ \end{aligned} decimos que \epsilon = (k) \, \sigma entonces la desigualdad quedaría de la siguiente manera, P[\mu_X - \epsilon < X < \mu_X + \epsilon] \geq 1 - \frac{\sigma_X^2}{\epsilon^2} para \epsilon > 0 y cualquier variable aleatoria X (denotando \mu_X = E[X] y \sigma^2_X = Var[X]).

¿De qué me sirven los anteriores resultados? ¿para qué los puedo utilizar?

Ejemplo 1 Supongamos que una fabrica produce 1500 unidades al día, con una desviación estándar de aproximadamente 300 unidades.

Entonces, sin importar la distribución (el mecanismo aleatorio detrás) de la variable aleatoria X: “número de unidades producidas por la fabrica al día”, podemos concluir que,

\begin{aligned} P[\mu_X - (k) \, \sigma_X < X < \mu_X + k \, \sigma_X] &\geq 1 - \frac{1}{k^2} \\ P[1500 - (k) (300) < X < 1500 + (k) (300)] &\geq 1 - \frac{1}{k^2} \end{aligned}

De allí (sin conocer nada más acerca de la variable aleatoria X) puedo asegurar que como mínimo el 84% de los días se producen entre 750 y 2250 unidades al día (llego a esta conclusión tomando k = 2.5).

Ejercicio 23 ¿A partir de la información el ejemplo anterior, como mínimo, qué PROPORCIÓN de los días se producirán entre 1000 y 2000 unidades?

Tip

Tome \epsilon = 500.

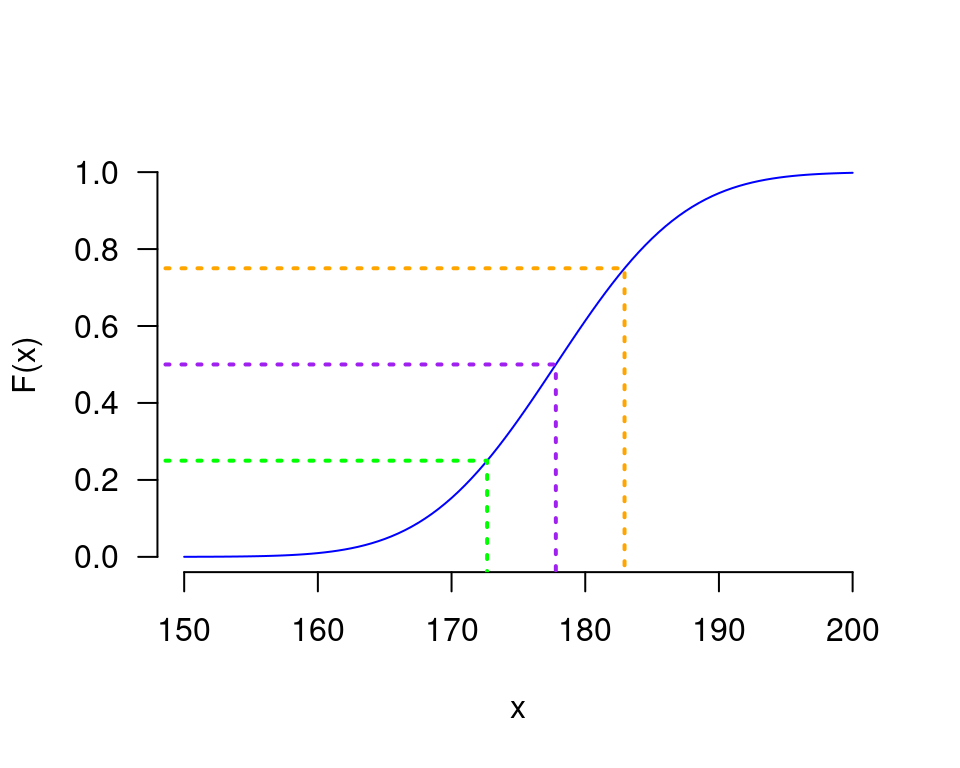
Ejemplo 2 Supongamos que la estatura media de los hombres adultos en cierto país es de aproximadamente 177.8 cm, con una desviación estándar de alrededor de 7.62 cm.

Entonces, sin importar la distribución (el mecanismo aleatorio detrás) de la variable aleatoria X: “estatura media de los hombres adultos”, se tiene que,

\begin{aligned} P[\mu_X - k \, \sigma_X < X < \mu_X + k \, \sigma_X] &\geq 1 - \frac{1}{k^2} \\ P[177.8 - 2 (7.62) < X < 177.8 + 2 (7.62)] &\geq 1 - \frac{1}{2^2} \\ P[162.56 < X < 193.04] &\geq 0.75 \end{aligned}

Es decir, al menos (como mínimo) el 75\% de los hombres adultos de ese cierto país tienen una estatura entre 162.56 y 193.04 cm.

Ejercicio 24 ¿A partir de la información el ejemplo anterior, entre qué estaturas estaría al menos (como mínimo) el 90\% de las estaturas de los hombres adultos de ese país?

Ejercicios

A continuación se encuentran una serie de ejercicios tomados del siguiente libro:

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación.

Ejercicio 25 (Walpole 4.1 (3.13))  

En el ejercicio 3.13 de la página 92 se presenta la siguiente distribución de probabilidad de X, el número de imperfecciones que hay en cada 10 metros de una tela sintética, en rollos continuos de ancho uniforme

x	0	1	2	3	4
f(x)	0.41	0.37	0.16	0.05	0.01

Calcule el número promedio de imperfecciones que hay en cada 10 metros de esta tela.

Ejercicio 26 (Walpole 4.13 (3.7))  

La función de densidad de la variable aleatoria continua X, el número total de horas que una familia utiliza una aspiradora durante un año, en unidades de 100 horas, se da en el ejercicio 3.7 de la página 92 como f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Calcule el número promedio de horas por año que las familias utilizan sus aspiradoras.

Ejercicio 27 (Walpole 4.21 (4.12))  

¿Cuál es la utilidad promedio por automóvil que obtiene un distribuidor, si la utilidad en cada uno está dada por g(X) = X^2, donde X es una variable aleatoria que tiene la función de densidad del ejercicio 4.12?

Ejercicio 4.12: Si la utilidad para un distribuidor de un automóvil nuevo, en unidades de $5000, se puede ver como una variable aleatoria X que tiene la siguiente función de densidad f(x) = \begin{cases} 2(1 - x) & 0 < x < 1 \\ 0 & \text{en otro caso} \end{cases} Calcule la utilidad promedio por automóvil.

Ejercicio 28 (Walpole 4.49 (4.32))  

Considere la situación del ejercicio 4.32 de la página 119. La distribución del número de imperfecciones por cada 10 metros de tela sintética está dada por

x	0	1	2	3	4
f(x)	0.41	0.37	0.16	0.05	0.01

Calcule la varianza y la desviación estándar del número de imperfecciones.

Ejercicio 29 (Walpole 4.58)  

El tiempo total que una adolescente utiliza su secadora de pelo durante un año, medido en unidades de 100 horas, es una variable aleatoria continua X que tiene la siguiente función de densidad f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Utilice las propiedades de valor esperado para evaluar la media de la variable aleatoria Y = 60X^2 + 39X, donde Y es igual al número de kilowatts-hora que gasta al año.

Ejercicio 30 (Walpole 4.75)  

Una empresa eléctrica fabrica una bombilla de luz de 100 watts que, de acuerdo con las especificaciones escritas en la caja, tiene una vida media de 900 horas con una desviación estándar de 50 horas. A lo sumo, ¿qué porcentaje de las bombillas no duran al menos 700 horas? Suponga que la distribución es simétrica alrededor de la media.

Funciónes generadora de momentos y característica

Definición 2 (Función generadora de momentos) Sea X una variable aleatoria tal que E \left[ \mathrm{e}^{tX} \right] es finito para todo t \in (-\alpha, \alpha), con \alpha real positivo. Se define la función generadora de momentos de X, denotada por m_X(\cdot) como: m_X(t) = E \left[ \mathrm{e}^{tX} \right] para t \in (-\alpha, \alpha).

Teorema 1 Si X es una variable aleatoria cuya función generadora de momentos existe, entonces, E \left[ X^r \right] existe para toda r \in \mathbb{Z}^+ (el recíproco no es válido).

Teorema 2 Si X es una variable aleatoria cuya función generadora de momentos m_X(\cdot) existe, entonces, existe h \in (0,\infty) tal que: m_X(t) = \sum_{k=0}^{\infty} \frac{E \left[ X^k \right]}{k!} t^k para todo t \in (-h,h), y por lo tanto, E \left[ X^k \right] = \left. \frac{d^r}{dt^r} m_X(t) \right|_{t=0}

Definición 3 (Función característica) Sea X una variable aleatoria. La función característica de X es la función \varphi_X : \mathbb{R} \longrightarrow \mathbb{C} definida por: \varphi_X(t) := E \left[ \mathrm{e}^{\mathrm{i}tX} \right] donde \mathrm{i} = \sqrt{-1} y \mathrm{e}^{\mathrm{i}tX} = \cos(tX) + \mathrm{i} \sin (tX).

Teorema 3 Si X es una variable aleatoria discreta o absolutamente continua entonces \varphi_X(t) existe para todo t \in \mathbb{R}.

Teorema 4 Sea X una variable aleatoria. La función característica \varphi_X(t) de X satisface:

• \varphi_X(0) = 1.
• \varphi_X(t) \leq 1 para todo t.
• Si E \left[ X^k \right] existe, entonces, \left. \frac{d^r}{dt^r} \varphi_X(t) \right|_{t=0} = \mathrm{i}^k \, E \left[ X^k \right].

Teorema 5 Si X y Y son variables aleatorias, y, \varphi_X(t) = \varphi_Y(t) para todo t, entonces, X y Y tienen la misma distribución.

EN CONSTRUCCION.

Ejercicios

Determine una expresión para la función característica de Y en términos de las constantes en los reales, la función característica de X o las funciones características de los X_i según corresponda.

1. Si Y = a \in \mathbb{R}, entonces $_Y(t) = $¿?
2. Si Y = a X + b, para a, b \in \mathbb{R}, entonces $_Y(t) = $¿?
3. X y Y son variables aleatorias independientes si y solo si $_{X+Y}(t) = $¿?
4. Si X_1, \dots, X_m es un conjunto de variables aleatorias independientes, a_1, \dots, a_m \in \mathbb{R} y Y = a_1 X_1 + \cdots + a_m X_m, entonces $_Y(t) = $¿?
5. Si X_1, \dots, X_n es una muestra aleatoria y Y = \bar{X}, entonces $_Y(t) = $¿?

EN CONSTRUCCION.