1 Principios de IE
En esta sección se hará una revisión de algunos temas relacionados con los principios de inferencia estadística.
1.1 Acerca de la estadística
1.1.1 El quehacer de la Estadística
Estadística: Recolección, presentación, análisis y uso de datos para la toma de decisiones y resolución de problemas.
La estadística gira alrededor de la incertidumbre (describir, entender, medir, controlar, establecer, explicar). Si no hay incertidumbre (aleatoriedad) entonces no hay estadística.
La estadística está al servicio de todas las áreas de conocimiento, en su búsqueda de entender la realidad por medio del análisis de datos y en donde la incertidumbre y variabilidad hacen parte de la naturaleza de dicha realidad/datos.
1.1.2 Definiciones
Variable: Una característica, propiedad o atributo observable que medimos.
Por ejemplo: Estatura, Edad, Ingresos, Transacciones.
Constructo o variable latente: Variable no observable. Concepto teórico que no se puede medir directamente.
Por ejemplo: Inteligencia, Felicidad, Inflación, PIB.
Individuo o unidad estadística: Los objetos o entidades a los que les pertenecen las variables. Objetos o entidades a los que se les mide directa o indirectamente las características, propiedades o atributos de interés.
Por ejemplo: Persona, Animal, Empresa, País, Año.
Población: Conjunto de todos los posibles individuos o unidades estadísticas de interés a los cuales se les podría obtener sus características, propiedades o atributos (sus valores para la(s) variable(s)).
Por ejemplo: Estudiantes de una asignatura para el presente semestre académico, Toros de lidia llevados a la Santamaría en las últimas dos décadas, Empresas textiles que tuvieron exportaciones en los últimos cinco años, Años que tuvieron vigente el programa “Bogotá Despierta” el día del amor y la amistad.
Muestra: Subconjunto de individuos o unidades estadísticas de la población.
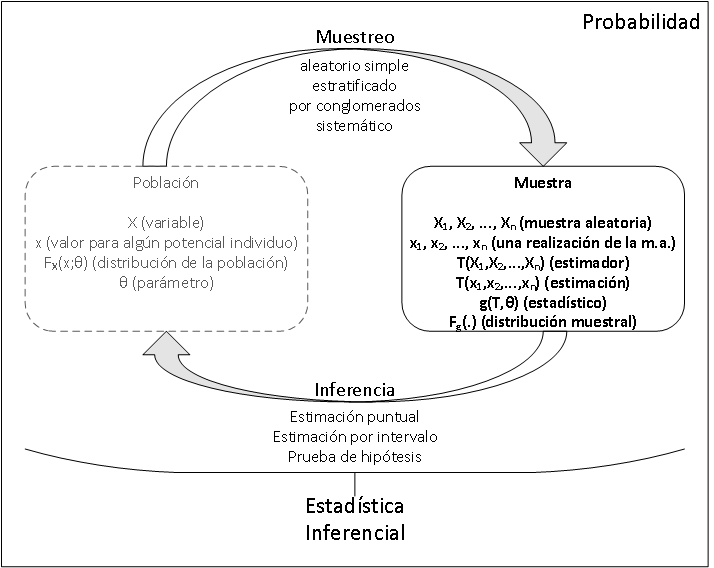
1.1.3 Relación entre estadística descriptiva, probabilidad, muestreo e inferencia
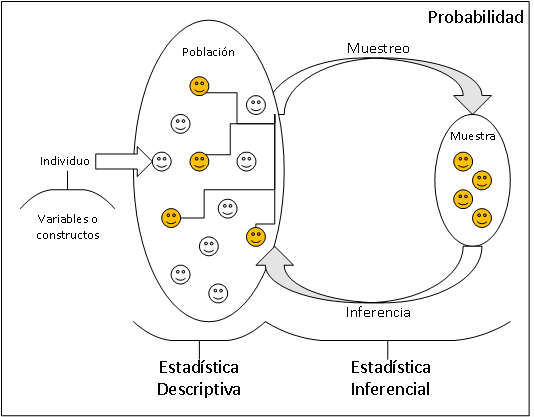
A partir del enunciado del siguiente ejercicio, identifique y reflexione acerca de los que serían los individuos, las variables, la población y la muestra, en cada caso.
Ejercicio 1.1
Defina las poblaciones adecuadas a partir de las cuales se seleccionaron las siguientes muestras:
Se llamó por teléfono a personas de 200 casas en la ciudad de Richmond y se les pidió nombrar al candidato por el que votarían en la elección del presidente de la mesa directiva de la escuela.
Se lanzó 100 veces una moneda y se registraron 34 cruces
Se probaron 200 pares de un nuevo tipo de calzado deportivo en un torneo de tenis profesional para determinar su duración y se encontró que, en promedio, duraron 4 meses.
En cinco ocasiones diferentes a una abogada le tomó 21, 26, 24, 22 y 21 minutos conducir desde su casa en los suburbios hasta su oficina en el centro de la ciudad.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 8.1.
1.2 Acerca del muestreo
- ¿Qué es una muestra?
- ¿Por qué se necesita una muestra?
1.2.1 Muestra aleatoria
Definición 1.1 (Muestra aleatoria) Si X_1, X_2, \dots, X_n son n variables aleatorias independientes e igualmente distribuidas con distribución F_X(x), entonces X_1, X_2, \dots, X_n es una muestra aleatoria, de tamaño n, de la población con distribución F_X(x).
¿Cómo puedo garantizar que, la manera en que selecciono los individuos, hace que la muestra sea en verdad aleatoria?
1.2.2 Muestreo aleatorio simple
Ejercicio 1.2
Fortune publica datos sobre ventas, valor del activo, valor de mercado y utilidades por acción de las 500 corporaciones industriales más grandes de Estados Unidos (Fortune 500, 2006). Suponga que usted desea seleccionar una muestra aleatoria simple de 10 corporaciones de la lista Fortune 500. Identifique los números de las 10 corporaciones que se tomarán para la muestra.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio 3.
Muestreo aleatorio simple (población finita): Una muestra aleatoria simple de tamaño n de una población finita de tamaño N es aquella que es seleccionada de tal manera que cada posible muestra (de tamaño n) tiene la misma probabilidad de ser seleccionada.
Muestreo aleatorio simple (población infinita): Cada individuo se selecciona de manera independiente.
Obtención de valores pseudoaleatorios “igualmente probables”:
- En la calculadora:
RAN# - Simple Random Sampling Applet
- Generate Random Numbers
- En una hoja de cálculo: Funciones
RAND()yRANDBETWEEN(a,b). - En el software estadístico R: Función
sample().
Piense (especule) acerca de cuál será la diferencia entre “valores aleatorios” y “valores pseudoaleatorios”, luego, investigue cuál es la diferencia y contraste con lo que había pensado (especulado) inicialmente.
1.2.3 Otros tipos de muestreo
Muestreo estratificado: En este caso los individuos de la población se pueden dividir en grupos (homogéneos en su interior y heterogéneos entre ellos) y se desea que en la muestra se tenga una representación adecuada de cada uno de estos grupos. Es así que se toma una muestra aleatoria simple de individuos de cada grupo, de tal manera que en la muestra se conserve la proporción de los tamaños de los grupos.
Muestreo por conglomerados: En este caso los individuos de la población están divididos en segmentos que no necesariamente son homogéneos, cada segmento es una buena representación en menor escala del comportamiento de toda la población y por lo tanto no es necesario tomar individuos de todos los segmentos. Es así que se toma una muestra aleatoria simple de los segmentos y luego para cada segmento seleccionado se toma una muestra aleatoria simple de individuos.
Muestreo sistemático: En este caso, los elementos de la población son seleccionados de manera sistemática a través de la población. La idea es tomar aleatoriamente un individuo por cada cierto número de individuos, es decir, tomo aleatoriamente un individuo de los primeros k, luego uno de los siguientes k y así sucesivamente.
1.3 Acerca de la inferencia estadística
Ejercicio 1.3 Lance una moneda 10 veces consecutivas, registrando los diez resultados obtenidos. Considere que dichos resultados son la realización de una muestra aleatoria de tamaño 10.
- ¿Cuál sería la población en esta situación?
- ¿Cuál sería la variable?
- ¿Cuál sería la distribución de la población?
- ¿Cuál sería el parámetro o los parámetros de dicha distribución?
1.3.1 Ideas iniciales
Estadístico: “Una función de una muestra aleatoria”.
Estimador: “Una función de una muestra aleatoria utilizada para estimar un parámetro o una función de un parámetro (no involucra o no tiene parámetros en su expresión)”.
Estimación: “Valor que toma un estimador teniendo en cuenta los valores que tomó la muestra aleatoria respectiva (que tomaron los datos observados)”.
1.3.2 Relación entre definiciones e ideas iniciales