2 Univariada
En esta sección se hará una revisión de algunos temas relacionados con el análisis descriptivo de datos variable por variable, es decir una variable a la vez. Este análisis descriptivo incluye representaciones tabulares y gráficas, medidas descriptivas e identificación de datos atípicos junto con la representación gráfica llamada diagrama de caja o boxplot.
- Lee todo el contenido de esta sección (Estadística Descriptiva, 2 Univariada).
- En tus propias palabras, has una exposición escrita detallada en tu cuaderno sobre cada parte de lo leído, como si le estuvieras explicando a un compañero o amigo. Recuerda que aprendemos aproximadamente el 95% de lo que tratamos de enseñar a otros.
- Anota cualquier duda o tema que te resulte confuso. ¡No te preocupes si no lo entiendes todo a la primera!
- Busca por tu cuenta respuestas a esas dudas. Esto te ayudará a llegar a clase con ideas para compartir.
- Lleva a clase: tu exposición escrita, tus dudas y las respuestas que encontraste. ¡Trabajaremos juntos para aclararlo todo!
2.1 Representación tabular y gráfica de una variable
Para una adecuada representación tabular o gráfica, debemos tener claramente identificados los individuos (unidades estadísticas), las variables y la escala de medida de cada una de las variables, del estudio o análisis de interés.
Una adecuada representación es importante para observar y trasmitir adecuadamente información valiosa presente en nuestros datos.
Aunque a continuación se presenta un ejemplo de aplicación muy particular, lo aprendido por medio de él se podrá extender fácilmente a las variables de cualquier contexto de aplicación, por ejemplo, uno relacionado con un tema de su interés.
Ejemplo de aplicación:
“La Universidad Nacional de Colombia selecciona, a los estudiantes que se admiten en cada semestre mediante la aplicación de un examen de admisión estructurado en cinco áreas: matemáticas, ciencias, sociales, textual e imágenes… Para este ejemplo se toman los resultados de los 445 admitidos a las siete carreras de la Facultad de Ciencias del primer semestre de 2013… La hoja de datos retenida para el ejemplo tiene en las columnas: la carrera, los resultados del examen en cada área y global, algunas variables sociodemográficas…”
Pardo, C. (2020). Estadística descriptiva multivariada. [online] Bogotá, Colombia: Universidad Nacional de Colombia. https://repositorio.unal.edu.co/handle/unal/79914
2.1.1 Variable nominal
| categorias | frec.abs. | frec.rel. | porcent. |
|---|---|---|---|
| Biol | 63 | 0.1416 | 14.16 |
| Esta | 66 | 0.1483 | 14.83 |
| Farm | 73 | 0.1640 | 16.40 |
| Fisi | 82 | 0.1843 | 18.43 |
| Geol | 45 | 0.1011 | 10.11 |
| Mate | 53 | 0.1191 | 11.91 |
| Quim | 63 | 0.1416 | 14.16 |
| TOTAL | 445 | 1.0000 | 100.00 |
La estructura genérica (“el esqueleto”) de la representación tabular de una variable nominal usualmente deberá tener la siguiente forma:
| x_i | f_i : Frecuencia absoluta | h_i : Frecuencia relativa |
|---|---|---|
| Una etiqueta | f_1 | \frac{f_1}{N} |
| Otra etiqueta | f_2 | \frac{f_2}{N} |
| \vdots | \vdots | \vdots |
| Última etiqueta | f_m | \frac{f_m}{N} |
| Total | f_1 + \cdots + f_m = N | \frac{f_1 + \cdots + f_m}{N} = \frac{N}{N} = 1 |
N: Cantidad total de unidades estadísticas / individuos.
m: Cantidad de valores que toma la variable (es decir, número de “etiquetas” distintas, y por ende, número de filas de la tabla).
La representación gráfica de una variable nominal puede ser mediante:
- Gráfica de barras (usando las frecuencias absolutas).
- Gráfica de pareto (gráfica de barras usando las frecuencias absolutas pero ordenando por dichas frecuencias absolutas).
- Gráfica de pastel (usando las frecuencias relativas).
2.1.2 Variable ordinal
| categorias | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| E0 | 2 | 0.0045 | 2 | 0.0045 |
| E1 | 36 | 0.0809 | 38 | 0.0854 |
| E2 | 141 | 0.3169 | 179 | 0.4022 |
| E3 | 185 | 0.4157 | 364 | 0.8180 |
| E4 | 72 | 0.1618 | 436 | 0.9798 |
| E5 | 8 | 0.0180 | 444 | 0.9978 |
| E6 | 1 | 0.0022 | 445 | 1.0000 |
| TOTAL | 445 | 1.0000 | NA | NA |
La estructura de la representación tabular de una variable ordinal usualmente tiene la siguiente forma:
| x_i | f_i : F. abs. | h_i : F. rel. | F_i : F. abs. acumulada | H_i: F. rel. acumulada |
|---|---|---|---|---|
| Etiqueta 1 | f_1 | \frac{f_1}{N} | f_1 | \frac{f_1}{N} |
| Etiqueta 2 | f_2 | \frac{f_2}{N} | f_1 + f_2 | \frac{f_1 + f_2}{N} |
| \vdots | \vdots | \vdots | \vdots | \vdots |
| Etiqueta m | f_m | \frac{f_m}{N} | f_1 + \cdots + f_m = N | \frac{f_1 + \cdots + f_m}{N} = \frac{N}{N} = 1 |
| Total | N | 1 | No aplica | No aplica |
La representación gráfica de una variable ordinal puede ser mediante:
- Gráfica de barras (usando las frecuencias absolutas y teniendo en cuenta uno de los dos posibles ordenamientos, el ascendiente o el descendiente).
- Gráfica de pastel (usando las frecuencias relativas).
En el siguiente enlace encontrarán otros ejemplos: https://istats.shinyapps.io/EDA_categorical/
2.1.3 Variable de intervalo
Supongamos que para 1500 individuos tuviésemos la variable: número de hijos en el hogar.
| valores | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| 0 | 419 | 0.2793 | 419 | 0.2793 |
| 1 | 255 | 0.1700 | 674 | 0.4493 |
| 2 | 375 | 0.2500 | 1049 | 0.6993 |
| 3 | 215 | 0.1433 | 1264 | 0.8427 |
| 4 | 127 | 0.0847 | 1391 | 0.9273 |
| 5 | 54 | 0.0360 | 1445 | 0.9633 |
| 6 | 24 | 0.0160 | 1469 | 0.9793 |
| 7 o más | 31 | 0.0207 | 1500 | 1.0000 |
- ¿Cuántas familias tienen menos de dos hijos?
- ¿Qué porcentaje de las familias tienen seis hijos o menos?
- ¿La mitad de las familias que menos hijos tiene, entre cuántos y cuántos hijos tiene? (¿El 50\% de las familias con menor cantidad de hijos tiene entre 0 y cuántos hijos?)
La estructura de la representación tabular de una variable de intervalo usualmente tiene la siguiente forma:
| x_i | f_i : F. abs. | h_i : F. rel. | F_i : F. abs. acumulada | H_i: F. rel. acumulada |
|---|---|---|---|---|
| Valor 1 | f_1 | \frac{f_1}{N} | f_1 | \frac{f_1}{N} |
| Valor 2 | f_2 | \frac{f_2}{N} | f_1 + f_2 | \frac{f_1 + f_2}{N} |
| \vdots | \vdots | \vdots | \vdots | \vdots |
| Valor m | f_m | \frac{f_m}{N} | N | 1 |
| Total | N | 1 | No aplica | No aplica |
Como las columnas / frecuencias incluidas en esta representación tabular coinciden con las del caso anterior (variable ordinal), entonces las posibilidades de representación gráfica también coinciden:
- Gráfica de barras.
- Gráfica de pastel.
2.1.4 Variable de razón
¿Para una variable con escala de medida de razón haríamos todo igual (representaciones tabulares y gráficas) que como lo hicimos para una variable con escala de medida de intervalo?
¿Qué pasaría si cada valor tomado por la variable con escala de medida de razón lo consideramos una fila de una representación tabular asociada a la variable?
| intervalo | frec.abs. | frec.rel. | frec.abs.acum. | frec.rel.acum. |
|---|---|---|---|---|
| [400,500] | 4 | 0.0090 | 4 | 0.0090 |
| (500,600] | 22 | 0.0494 | 26 | 0.0584 |
| (600,700] | 166 | 0.3730 | 192 | 0.4315 |
| (700,800] | 187 | 0.4202 | 379 | 0.8517 |
| (800,900] | 55 | 0.1236 | 434 | 0.9753 |
| (900,1000] | 5 | 0.0112 | 439 | 0.9865 |
| (1000,1100] | 5 | 0.0112 | 444 | 0.9978 |
| (1100,1200] | 1 | 0.0022 | 445 | 1.0000 |
La estructura para una representación tabular de una variable de razón podría tener la siguiente forma:
| I_i | f_i | h_i | F_i | H_i |
|---|---|---|---|---|
| Intervalo 1 | f_1 | \frac{f_1}{N} | f_1 | \frac{f_1}{N} |
| Intervalo 2 | f_2 | \frac{f_2}{N} | f_1 + f_2 | \frac{f_1 + f_2}{N} |
| \vdots | \vdots | \vdots | \vdots | \vdots |
| Intervalo m | f_m | \frac{f_m}{N} | N | 1 |
| Total | N | 1 | No aplica | No aplica |
Teniendo en cuenta que nos tocaría trabajar con intervalos, ¿qué mecanismo o qué criterio debemos usar para escoger o definir esos intervalos?
Si definimos cuál será la cantidad de intervalos, es decir cuál será el número de filas que tendrá la tabla, entonces es muy fácil obtener luego los intervalos.
Existen varias opciones o recomendaciones para seleccionar la cantidad de intervalos:
- m, un valor entre 5 y 15
- m = \sqrt{N}
- m = 1 + (3.322) \log_{10}(N) (Fórmula de Sturges)
El criterio más importante para establecer los intervalos a usar es el anticipar y el pensar cuáles serían los intervalos que conducirán a la representación tabular resultante más sencilla, más clara, más informativa y más fácil de leer y entender para las personas a las que estaría dirigida dicha representación tabular.
Sin embargo, una manera “mecánica” o “automática” para obtener unos intervalos podría ser la siguiente: La longitud o el tamaño de cada intervalo podría estar dado por la fórmula, L = \frac{ \max\{x_1, x_2, \dots, x_N\} - \min\{x_1, x_2, \dots, x_N\} }{ m } y como consecuencia, los m intervalos podrían estar dados por las siguientes fórmulas, \Big[\min \, , \, \min+L\Big] \\ \Big(\min+L \, , \, \min+2L\Big] \\ \Big(\min+2L \, , \, \min+3L\Big] \\ \dots \\ \Big(\min+(m-2)L \, , \, \min+(m-1)L\Big] \\ \Big(\min+(m-1)L \, , \, \min+mL=\max\Big]
La representación gráfica de las frecuencias absolutas, dadas por los intervalos obtenidos, se denomina histograma. Note que en el histograma, las “barras” están “pegadas entre sí” lo cual permite representar la posibilidad de la variable de tener valores en los números reales, tener valores que se podrían ubicar en cualquier parte del eje x.
La selección del número de intervalos (o del ancho de cada uno) en un histograma no tiene una regla única y estricta; en buena medida, es una decisión relativamente subjetiva. El propósito aquí es lograr un equilibrio entre el sintetizar la información de manera que sea comprensible y la fidelidad al comportamiento de los datos: un número reducido de intervalos puede ocultar patrones relevantes, mientras que un número excesivo puede dificultar la construcción, visualización e interpretación. La clave está en resumir la información de forma que sea útil y fácil de entender para el lector, pero sin perder demasiado detalle que sea relevante.
El histograma nos permite observar la forma (figura) en que los datos podrían estar “repartidos” sobre el eje x, imaginando el caso en el que tuviese infinitos valores a lo largo de todo el eje x. Nos permite ver en dónde habrían más y en dónde habría menos, es decir podríamos visualizar su “densidad” (en dónde es más denso y en dónde es menos denso).
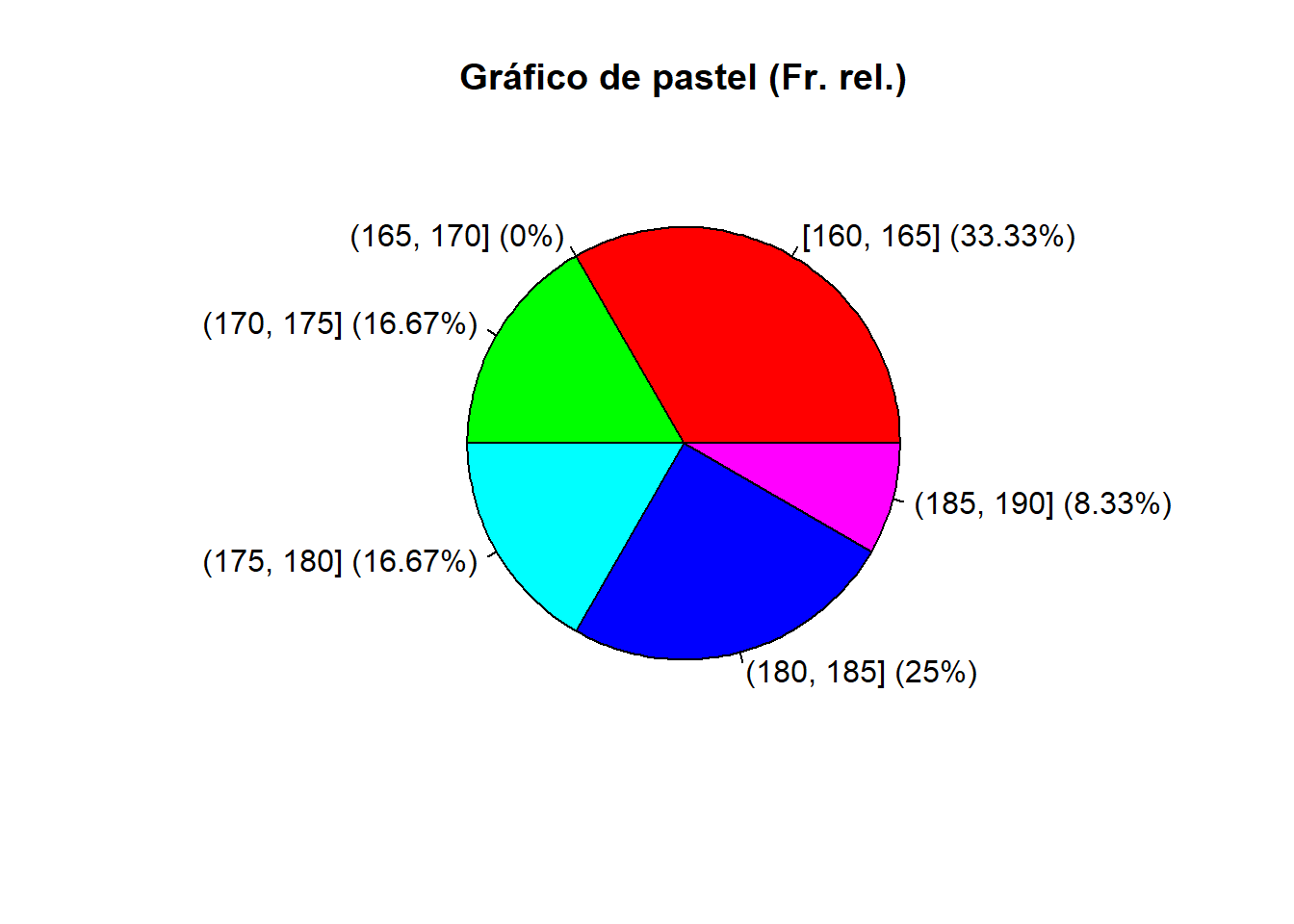
Ejercicio 2.1 Estatura de (un grupo de) personas
Valores de la variable para un cierto conjunto de individuos (datos ordenados): 160; 163; 163; 165; 172; 174; 178; 180; 184; 184; 185; 189.
Representación tabular:
| I_i | \tilde{x}_i | f_i | h_i | F_i | H_i |
|---|---|---|---|---|---|
| [160,165] | 162.5 | 4 | 0.3333 | 4 | 0.3333 |
| (165,170] | 167.5 | 0 | 0.0000 | 4 | 0.3333 |
| (170,175] | 172.5 | 2 | 0.1667 | 6 | 0.5000 |
| (175,180] | 177.5 | 2 | 0.1667 | 8 | 0.6667 |
| (180,185] | 182.5 | 3 | 0.2500 | 11 | 0.9167 |
| (185,190] | 187.5 | 1 | 0.0833 | 12 | 1 |
| Total | No aplica | 12 | 1 | No aplica | No aplica |
En algunos contextos y situaciones, \tilde{x}_i se utiliza como un valor que va a representar al intervalo completo.
Representaciones gráficas:
2.2 Medidas descriptivas
2.2.1 Posición
¿Cómo podría responder preguntas como esta o similares, usando los datos que se tienen (por ejemplo, de los puntajes en el examen)?: Si se decide proporcionar apoyo adicional al 12% de los estudiantes con los puntajes más bajos, ¿cuál sería el puntaje de corte para proporcionar o no ese apoyo?
El cuantil 0.12 \left(x_{p=0.12}\right) es el valor para la variable, que marca un corte de tal manera que el 12\% de los valores que se tienen de la variable son menores o iguales al valor del cuantil, y el 88\% restante de los valores de la variable son mayores o iguales al valor del cuantil. En el caso de la variable exam, se podría considerar que el cuantil 0.12 es igual a un puntaje de x.p (los admitidos con puntaje en el examen menor a x.p serían a los que se les proporcionaría apoyo adicional).
Cuantil: Es un valor asociado a la variable, que denominaremos x_p para p \in [0,1], el cual indica que al menos el p \times 100 \% de los datos son menores o iguales que x_p y al menos el \left(1-p\right) \times 100 \% son mayores o iguales que x_p.
Existen una serie de cuantiles importantes o de uso más frecuente:
-
Cuartiles: Dividen los datos en cuatro partes iguales
\min_i\{x_i\} = x_{min} \\ x_{0.25} = Q_1 \\ x_{0.5} = Q_2 \\ x_{0.75} = Q_3 \\ \max_i\{x_i\} = x_{max}
-
Quintiles: Dividen los datos en cinco partes iguales
x_{min}; x_{0.2}; x_{0.4}; x_{0.6}; x_{0.8}; x_{max}
-
Deciles: Dividen los datos en diez partes iguales
x_{min}; x_{0.1}; x_{0.2}; \dots; x_{0.8}; x_{0.9}; x_{max}
-
Percentiles: Dividen los datos en cien partes iguales
x_{min}; x_{0.01}; x_{0.02}; \dots; x_{0.98}; x_{0.99}; x_{max}
Generalmente múltiples valores cumplen la definición de cuantil, por lo tanto no hay una única forma para calcularlo.
En su artículo, Hyndman y Fan (1996) hacen una revisión de nueve (9) alternativas de cálculo para un cuantil x_p deseado. Cada una de ellas tiene sus ventajas y desventajas desde la teoría estadística, en el artículo referenciando se mencionan dichas ventajas y desventajas.
Hablemos de las formas de cálculo que denominaremos: “Alternativa 6” y “Alternativa 7”:
“Alternativa 6”: Es la que usan en:
- Excel. Desde Office 2013 es la función PERCENTILE.EXC.
- SPSS.
- Minitab.
- Libro de Mendenhall.
“Alternativa 7”: Es la que usan en:
- Excel. Desde Office 2013 es la función PERCENTILE.INC (antes era la función PERCENTILE).
- R. Es la opción predeterminada, pero se puede seleccionar cualquiera de las nueve del artículo mencionado.
Para realizar el cálculo respectivo, los pasos a seguir serían los siguientes:
Tomar los datos x_1; x_2; \dots; x_N y ordenarlos x_{(1)}; x_{(2)}; \dots; x_{(N)}
-
“Alternativa 6”: Calcular i = (N+1) \, p.
“Alternativa 7”: Calcular i = (N-1) \, p + 1.
-
Dependiendo del valor de i:
Si es entero, entonces:
- x_p = x_{(i)}.
Si NO es entero, entonces:
Calcular: \lfloor i \rfloor (función piso: entero inmediatamente inferior a i) y \lceil i \rceil (función techo: entero inmediatamente superior a i).
Obtener x_{(\lfloor i \rfloor)} y x_{(\lceil i \rceil)} (los x’s de las posiciones respectivas en el ordenamiento).
Calcular x_p = x_{(\lfloor i \rfloor)} + \left(x_{(\lceil i \rceil)}-x_{(\lfloor i \rfloor)}\right) \, (i - \lfloor i \rfloor) (el valor que corresponda por interpolación lineal, sin importar si el valor obtenido se encuentra o no entre el conjunto de datos).
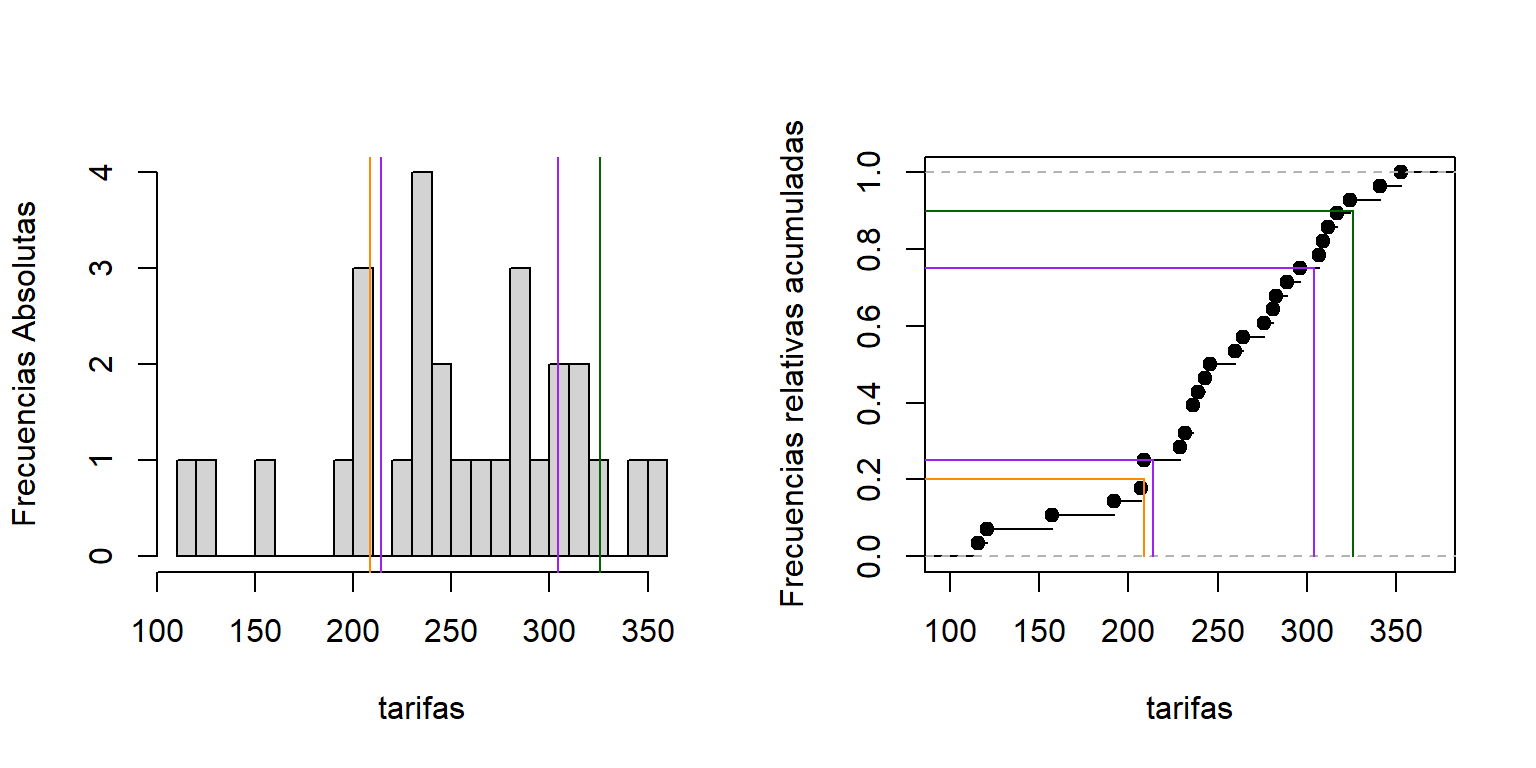
Ejercicio 2.2 La siguiente información corresponde a las tarifas por hora (en miles de pesos colombianos) cobradas por profesionales universitarios recién graduados, que ofrecen servicios de consultoría independiente, en temas relacionados con sus áreas de formación.
116; 121; 157; 192; 207; 209; 209; 229; 232; 236; 236; 239; 243; 246;\\ 260; 264; 276; 281; 283; 289; 296; 307; 309; 312; 317; 324; 341; 353.
A partir de los datos que se tienen, se desea establecer una categoría de “tarifas bajas” en donde se espera que en adelante queden incluidas el 20\% de las tarifas más bajas. ¿Cuál debería ser el valor de corte máximo para que una tarifa sea clasificada como baja?
También se busca identificar “tarifas de alto costo”, es decir, aquellas que por ejemplo se encuentren dentro del 10\% más alto. ¿A partir de qué valor una tarifa puede considerarse de alto costo?
Con el objetivo de caracterizar el comportamiento del mercado, se quiere determinar el rango en el que se ubican las tarifas del 50\% central. ¿Entre qué y qué valor se encuentran estas tarifas intermedias?
208.6 (naranja)
325.7 (verde)
214 y 304.25 (morado)
2.2.2 Centralidad
Existen varias medidas descriptivas que representan la centralidad de los datos, cada una de ellas de diferente manera.
Moda: Categoría(s) o valore(s) que tiene(n) la frecuencia más alta. Si la moda es un sólo valor entonces el conjunto de datos es unimodales, si varios valores son la moda entonces los datos son multimodales.
Mediana: Es el cuantil 0.5 (segundo cuartil, percentil 50), es decir que el 50% de los valores de la variable serían menores o iguales a la mediana y el 50% restante serían mayores o iguales a la mediana (“La mediana es el valor que divide los datos 50/50”). \mathrm{Mediana} = x_{0.5}
Media, media aritmética o promedio: Es como tomar una partecita, la N-ésima parte, de cada valor y luego sumarlas. También se puede interpretar como un centro de gravedad o punto de equilibrio. \mu = \frac{x_1}{N} + \frac{x_2}{N} + \dots + \frac{x_N}{N} = \frac{1}{N} \sum_{i=1}^{N} x_i
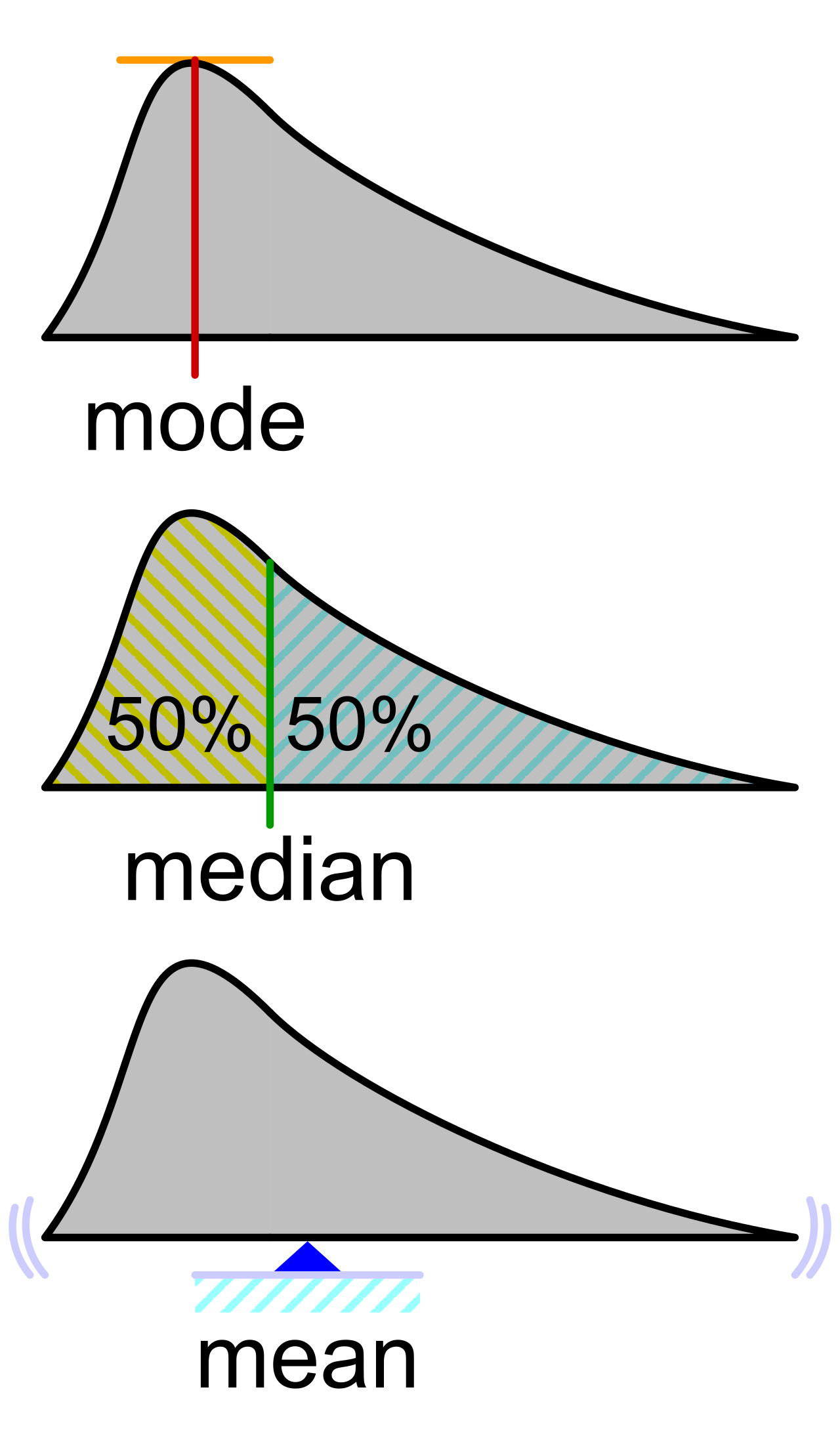
En el siguiente enlace se puede explorar el cómo cambian la media y la mediana para diferentes conjunto de datos: https://istats.shinyapps.io/MeanvsMedian/
Ejercicio 2.3 La siguiente información corresponde a las tarifas por hora (en miles de pesos colombianos) cobradas por profesionales universitarios recién graduados, que ofrecen servicios de consultoría independiente, en temas relacionados con sus áreas de formación.
116; 121; 157; 192; 207; 209; 209; 229; 232; 236; 236; 239; 243; 246;\\ 260; 264; 276; 281; 283; 289; 296; 307; 309; 312; 317; 324; 341; 353.
¿A partir de los datos de este ejercicio, qué valores toman las tres medidas de centralidad?
\begin{aligned} \mathrm{Moda} &= 209 \text{ y } 236 \\ \mu &= 253 \\ x_{0.5} &= 253 \end{aligned}
Si resulta que la tarifa de 353 fue erróneamente digitada y el verdadero valor es 853, ¿qué tanto cambian las tres medidas de centralidad?
La única medida de centralidad que cambia es la media (aumenta la cantidad que aporta el individuo que cambió de valor y naturalmente también cambia el centro de gravedad).
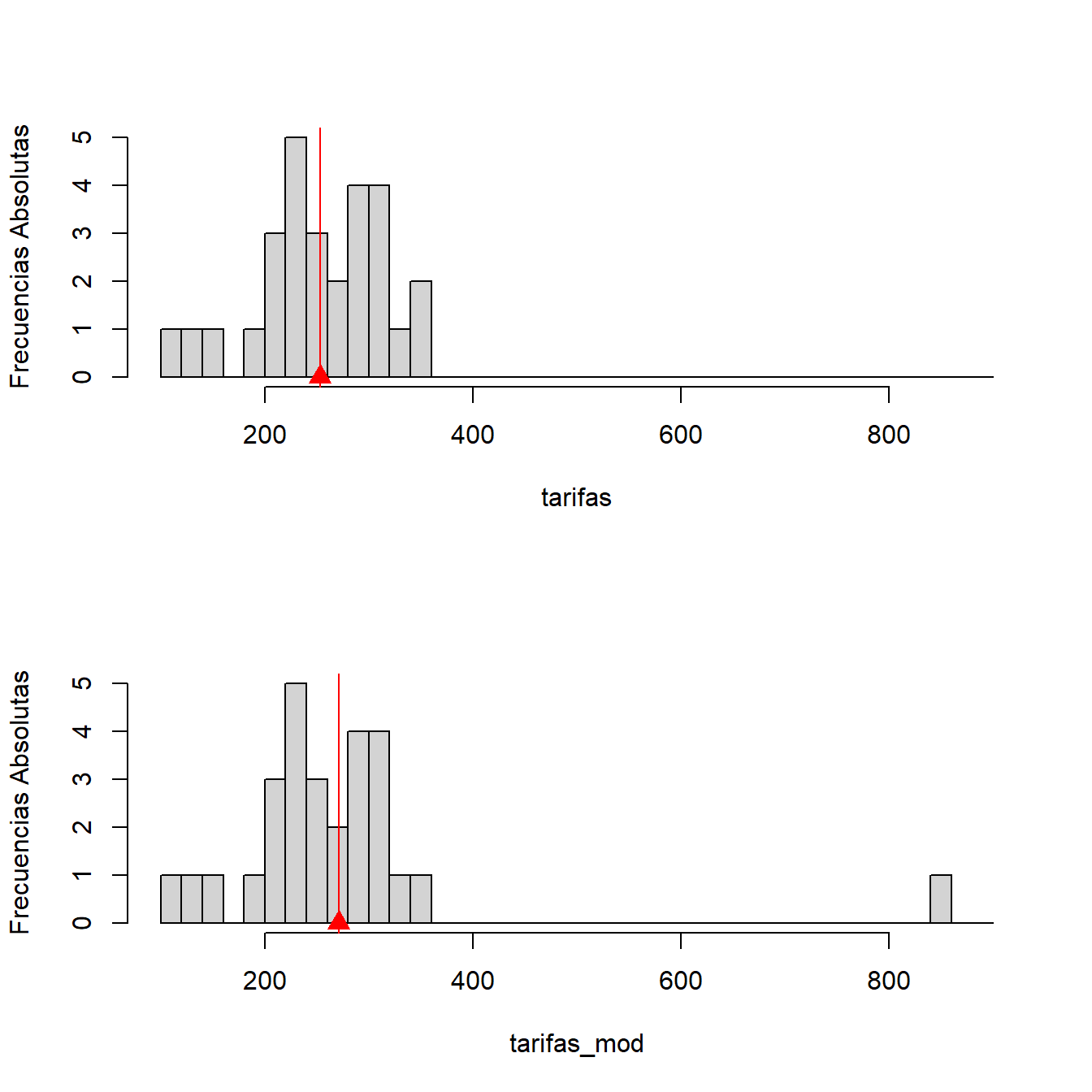
La media era 253, y con el cambio de valor de 353 a 853, ahora es 270.8571.

2.2.3 Dispersión
Las medidas descriptivas de dispersión deben representar una mayor o menor concentración de los datos.
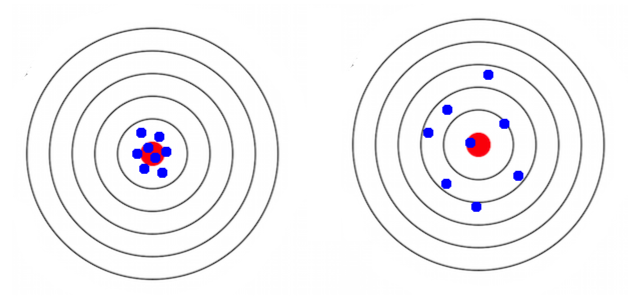
Rango: Magnitud en la cual oscilan todos los valores que toma la variable. R = x_{max} - x_{min} Es muy sensible a valores extremos. Es una medida que está en las mismas unidades que la variable.
Rango Intercuartílico: Magnitud en la cual oscilan el 50\% de los valores centrales que toma la variable. \mathrm{RIC} = Q_3 - Q_1 = x_{0.75} - x_{0.25} Está en las mismas unidades que la variable.
Varianza: Promedio de las desviaciones al cuadrado de cada dato con respecto a la media \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} \left( x_i - \mu \right)^2 Sensible a valores extremos. Está en unidades al cuadrado.
Pero, ¿qué representa la varianza?
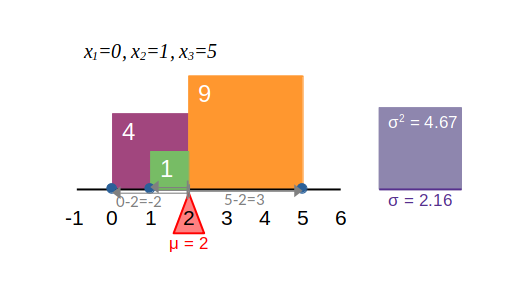
Desviación estándar: Raíz cuadrada positiva de la varianza. \sigma = \sqrt{\sigma^2}, \qquad \sigma \in \mathbb{R}^+ \cup {0} A partir de la varianza obtenemos la desviación estándar, que es una medida de dispersión que está en la mismas unidades de la variable.
Ejercicio 2.4
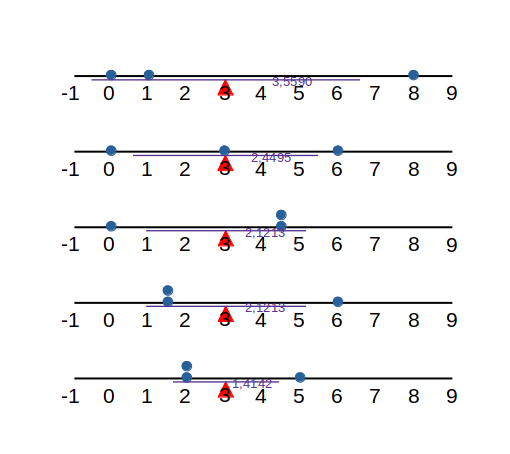
- Si x_1 = 0, x_2 = 1, x_3 = 8 entonces \mu =¿? y \sigma =¿?.
- Si x_1 = 0, x_2 = 3, x_3 = 6 entonces \mu =¿? y \sigma =¿?.
- Si x_1 = 0, x_2 = 4.5, x_3 = 4.5 entonces \mu =¿? y \sigma =¿?.
- Si x_1 = 1.5, x_2 = 1.5, x_3 = 6 entonces \mu =¿? y \sigma =¿?.
- Si x_1 = 2, x_2 = 2, x_3 = 5 entonces \mu =¿? y \sigma =¿?.
¿Qué observa a partir de los valores obtenidos?
Coeficiente de variación: Mide la variabilidad dada por la desviación estándar con respecto a la magnitud de la media. \mathrm{CV} = \frac{\sigma}{| \mu |}, \qquad \mu \neq 0 El coeficiente de variación da una idea de variabilidad relativa. Es una cantidad que no tiene asociada alguna unidad (se cancelan las unidades del numerador con las del denominador). Frecuentemente se da o se interpreta como un porcentaje (es una razón en donde el numerador no es parte del denominador para que pueda ser considerada como una proporción, y que al multiplicarla por cien se traduzca a un porcentaje). Es útil para comparar la dispersión de dos o más variables.
Ejercicio 2.5 La siguiente información corresponde a las tarifas por hora (en miles de pesos colombianos) cobradas por profesionales universitarios recién graduados, que ofrecen servicios de consultoría independiente, en temas relacionados con sus áreas de formación.
116; 121; 157; 192; 207; 209; 209; 229; 232; 236; 236; 239; 243; 246;\\ 260; 264; 276; 281; 283; 289; 296; 307; 309; 312; 317; 324; 341; 353.
¿A partir de los datos de este ejercicio, qué valores toman las diferentes medidas de variabilidad?
\begin{aligned} R &= 237 \\ \mathrm{RIC} &= 90.25 \\ \sigma^2 &= 3535.71 \\ \sigma &= 59.46 \\ \mathrm{CV} &= 0.2350 \end{aligned}\
¿Qué medidas cambian al cambiar la tarifa de 353 por una de 853?
Lo poblacional y lo muestral no son lo mismo, ni en la práctica, ni mucho menos conceptualmente. Por tal razón me gusta explicítamente hacer una diferencia entre los dos, teniendo símbolos distintos para cada caso, incluso para cuando las fórmulas son aparentemente las mismas. La mayoría de los libros no hace esta diferenciación, lo que creo puede llevara a confusiones.
Por lo anterior, a continuación encontraran un enlace a un documento .pdf con fórmulas, ecuaciones y símbolos tanto muestrales como poblacionales: FormulasPoblacionalMuestral.pdf
2.2.4 Forma (Opcional)
Coeficiente de asimetría (de Pearson): Indica el grado de asimetría de los datos C_{As} = \frac{\frac{1}{N} \sum_{i=1}^{N} \left( x_i - \mu \right)^3}{\sigma^3}, \qquad \sigma \neq 0
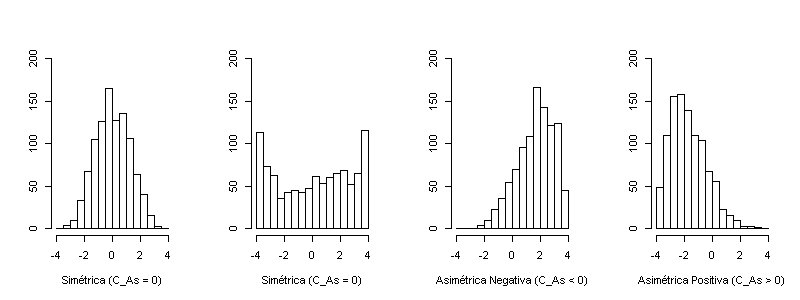
Coeficiente de apuntamiento (de Fisher) o exceso de curtosis: Indica el grado de apuntamiento de los datos con respecto al apuntamiento de la distribución normal (Campana de Gauss). C_{Ap} = \frac{\frac{1}{N} \sum_{i=1}^{N} \left( x_i - \mu \right)^4}{\sigma^4} - 3, \qquad \sigma \neq 0
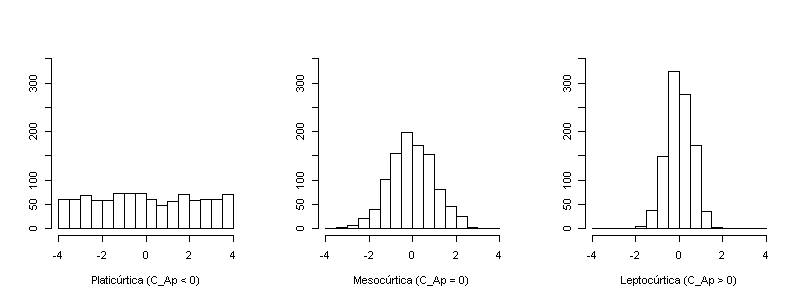
En la siguiente hoja de cálculo (Google Sheets) encontrarán un ejemplo relacionado con el cálculo de media, varianza, desviación estándar, coeficiente de asimetría y exceso de curtosis: EjemploCalculosMedidasDescriptivasUnaVariable.gsheet
2.3 Datos atípicos y diagrama de caja (boxplot)
2.3.1 Datos atípicos
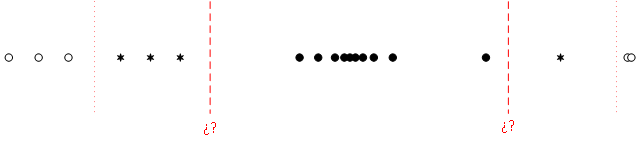
Un dato atípico (outlier) (bajo la definición de John Tukey) es aquel cuyo valor x_i cumple que: x_i < Q_1 - 1.5 (\mathrm{RIC}) \quad \text{ o } \quad x_i > Q_3 + 1.5 (\mathrm{RIC})
Los datos atípicos se pueden clasificar en dos grupos:
-
Datos atípicos extremos (far out) son aquellos tales que,
x_i < Q_1 - 3 (\mathrm{RIC}) \quad \text{ o } \quad x_i > Q_3 + 3 (\mathrm{RIC})
-
Datos atípicos leves o no extremos son aquellos tales que,
Q_1 - 3 (\mathrm{RIC}) < x_i < Q_1 - 1.5 (\mathrm{RIC}) \\ \text{ o } \\ Q_3 + 1.5 (\mathrm{RIC}) < x_i < Q_3 + 3 (\mathrm{RIC})
Ejercicio 2.6 La siguiente información corresponde a las tarifas por hora (en miles de pesos colombianos) cobradas por profesionales universitarios recién graduados, que ofrecen servicios de consultoría independiente, en temas relacionados con sus áreas de formación.
116; 121; 157; 192; 207; 209; 209; 229; 232; 236; 236; 239; 243; 246;\\ 260; 264; 276; 281; 283; 289; 296; 307; 309; 312; 317; 324; 341; 353.
¿Hay datos atípicos en este conjunto de datos?
Como tenemos que,
\begin{aligned} Q_1 &= 214 \\ Q_3 &= 304.25 \\ \mathrm{RIC} &= 90.25 \\ \end{aligned}\ Entonces los cuatro umbrales (puntos de referencia para saber si un dato es atípico, ya sea leve o extremo) son: \begin{aligned} Q_1 - 3 (\mathrm{RIC}) &= -56.75 \\ Q_1 - 1.5 (\mathrm{RIC}) &= 78.625 \\ Q_3 + 1.5 (\mathrm{RIC}) &= 439.625 \\ Q_3 + 3 (\mathrm{RIC}) &= 575 \end{aligned}\
Como no hay datos menores a 78.625, ni datos mayores a 439.625 entonces ningún dato es atípico (como no hay datos menores a -56.75, ni datos mayores a 575 entonces ningún dato es atípico extremo).
¿Qué ocurrirá al cambiar la tarifa de 353 por una de 853?
2.3.2 Diagrama de caja
El diagrama de caja (boxplot) es una representación gráfica que se construye a partir del llamado resumen de cinco números, resumen compuesto por todos los cuartiles: x_{min}; Q_1=x_{0.25}; Q_2=x_{0.5}; Q_3=x_{0.75}; x_{max}. El diagrama de caja también nos permite identificar o señalar datos atípicos.
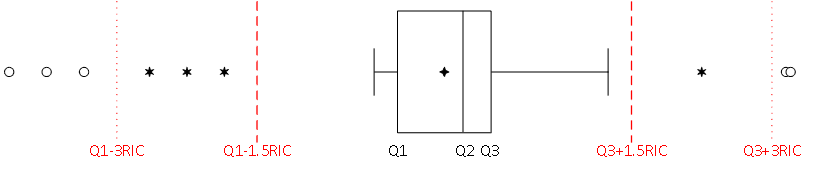
Ejercicio 2.7 La siguiente información corresponde a las tarifas por hora (en miles de pesos colombianos) cobradas por profesionales universitarios recién graduados, que ofrecen servicios de consultoría independiente, en temas relacionados con sus áreas de formación.
116; 121; 157; 192; 207; 209; 209; 229; 232; 236; 236; 239; 243; 246;\\ 260; 264; 276; 281; 283; 289; 296; 307; 309; 312; 317; 324; 341; 353.
Elabore un diagrama de caja a partir de los datos de este ejercicio. Compare con el diagrama de caja que se obtiene al cambiar la tarifa de 353 por una de 853.
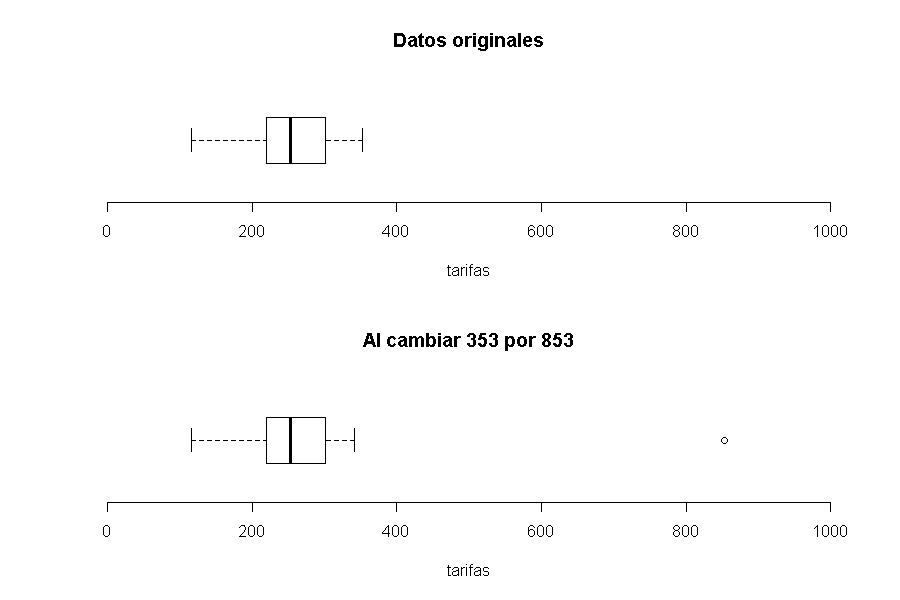
Ejercicio 2.8 ¿Qué puede decir o concluir a partir de lo que observa en cada uno de los siguientes gráficos?
En el siguiente enlace encontrarán más ejemplos: https://istats.shinyapps.io/EDA_quantitative/
En la parte de Estadística Descriptiva Univariada, la mayoría de los libros hablan acerca del Teorema de Chebyshev y La Regla Empírica. Sin embargo, como para mí no tiene sentido presentarles algo sin que se entienda el porqué de las cosas y teniendo en cuenta que se requieren ciertas bases de probabilidad para explicar y entender el porqué asociado a esos dos temas, entonces los veremos más adelante (cuando tengan las bases de probabilidad requeridas).
- No olvides seleccionar y resolver ejercicios de un libro acerca de lo visto en esta sección (preferiblemente que tengan respuesta). Por ejemplo, selecciona ejercicios con respuesta de los capítulos 1 y 2 del libro de Mendenhall o de las secciones 2.1, 2.2, 2.3, 3.1, 3.2, 3.3 y 3.4 del libro de Anderson.
- Aprende a usar tu calculadora para ingresar un conjunto de datos y obtener ágilmente como mínimo la media (\mu) y la desviación estándar poblacional (\sigma), sin tener que volver a ingresar el conjunto de datos más de una vez.
De manera opcional, quien quiera puede buscar y leer acerca de los siguientes temas adicionales:
- Gráfico de puntos.
- Gráfico de tallos y hojas.
- Otros gráficos que sirvan para representar una variable.
- Cómo producir representaciones tabulares y gráficas por medio de una hoja de cálculo (y/o por medio de alguna herramienta informática como por ejemplo R https://cran.r-project.org/).
- Otras medidas descriptivas de centralidad: Media ponderada, media recortada, media geométrica, media armónica.
- Otras medidas descriptivas de dispersión: Desviación media, desviación mediana.
- Otras medidas de asimetría y apuntamiento.
- Cálculo de medidas descriptivas con datos agrupados.