1 Definiciones iniciales
En esta sección se hará una introducción a una serie de conceptos y definiciones iniciales en estadística con el objetivo de orientar, contextualizar y sentar las bases para todos los temas que se verán en el curso.
- Lee el Capítulo 1 del libro: Estadística para las ciencias sociales. Ferris J. Ritchey (2008). (2a Ed.) McGraw-Hill. Es una excelente forma de empezar el curso.
- Lee todo el contenido de esta sección (Preliminares, 1 Definiciones Iniciales).
- En tus propias palabras, has una exposición escrita detallada en tu cuaderno sobre cada parte de lo leído, como si le estuvieras explicando a un compañero o amigo. Recuerda que aprendemos aproximadamente el 95% de lo que tratamos de enseñar a otros.
- Anota cualquier duda o tema que te resulte confuso. ¡No te preocupes si no lo entiendes todo a la primera!
- Busca por tu cuenta respuestas a esas dudas. Esto te ayudará a llegar a clase con ideas para compartir.
- Lleva a clase: tu exposición escrita, tus dudas y las respuestas que encontraste. ¡Trabajaremos juntos para aclararlo todo!
1.1 Introducción
1.1.1 El método científico
Objetivo: Resolver problemas de interés en un área mediante la aplicación eficiente de principios científicos.
- Describir el problema o fenómeno.
- Identificar factores importantes alrededor del problema y de la posible solución.
- Postular una tesis (proponer un modelo) usando el conocimiento del fenómeno y estableciendo supuestos y limitaciones.
- Realizar experimentos apropiados y recolectar los datos asociados.
- Validar o rechazar la tesis planteada (validar o rechazar el modelo planteado).
- Establecer conclusiones y recomendaciones, así como posiblemente proponer una nueva tesis (lo que llevaría a un nuevo paso 3. en adelante).
Los modelos (las variables dentro de los modelos) son de dos tipos: Deterministas o Aleatorios.
1.1.2 El quehacer de la Estadística
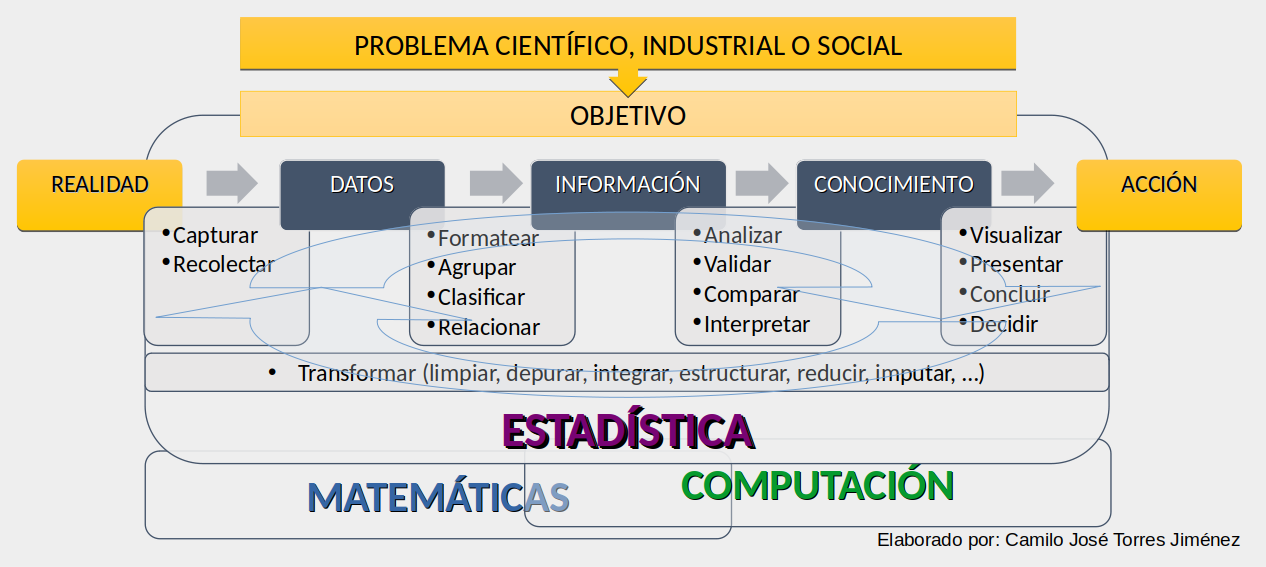
¿Estadística?
Cuerpo de conceptos y métodos empleados para la recolección e interpretación de datos acerca de un área particular de investigación y, a partir de ellos, obtener conclusiones en situaciones donde la incertidumbre y variación están presentes.
El objetivo de la estadística moderna abarca la recolección, presentación y caracterización de información para ayudar tanto en el análisis de datos como en el proceso de toma de decisiones.
La estadística está al servicio de todas las áreas de conocimiento, en su búsqueda de entender la realidad por medio del análisis de datos y en donde la incertidumbre y variabilidad hacen parte de la naturaleza de dicha realidad/datos.
La estadística gira alrededor de la incertidumbre (describir, entender, medir, controlar, establecer, explicar). Si no hay incertidumbre (aleatoriedad) entonces no hay estadística.
¿Datos?
Los conjuntos de datos más sencillos son los denominados datos estructurados, los cuales podemos encontrar en una tabla de datos simple como la siguiente:
1.1.3 Definiciones
Individuo o unidad estadística: Es la unidad básica de observación y análisis en un estudio estadístico.
Por ejemplo: Persona, Animal, Empresa, País, Año.
Variable: Característica, propiedad o atributo de cada individuo o unidad estadística, que puede tomar distintos valores entre ellos.
Por ejemplo: Estatura, Edad, Ingresos, Transacciones.
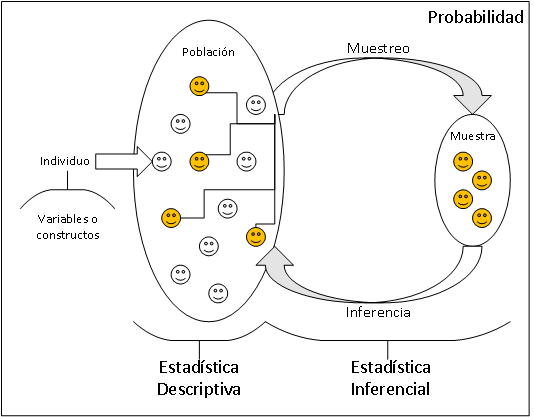
Población: Conjunto de todos los individuos o unidades estadísticas sobre los cuales se desea estudiar una o más variables. Se define en función del objetivo del estudio.
Por ejemplo: Estudiantes de la asignatura 1000013-B para el presente semestre académico, Toros de lidia llevados a la Santamaría en las últimas dos décadas, Empresas textiles que tuvieron exportaciones en los últimos cinco años, Años que tuvieron vigente el programa “Bogotá Despierta” el día del amor y la amistad.
Censo: Procedimiento mediante el cual se recopila información de interés sobre todos los elementos de una población.
- Ventaja: Se dispone de información completa, por lo que no hay incertidumbre asociada al desconocimiento de datos.
- Desventaja: Suele implicar altos costos en términos de tiempo, recursos humanos y dinero.
Muestra: Subconjunto de individuos o unidades estadísticas de la población, seleccionados mediante un procedimiento definido, para los cuales se recopilan datos con el propósito de realizar inferencias estadísticas válidas sobre la población de origen.
- Ventaja: Permite obtener información útil a menor costo y en menor tiempo que un censo.
- Desventaja: Al no incluir toda la población, las conclusiones están sujetas a incertidumbre, y la validez de las inferencias depende de la calidad del diseño muestral y del análisis estadístico.
Constructo o variable latente: Variable que no puede observarse ni medirse directamente, y cuyo estudio requiere recurrir a otras variables observables relacionadas con ella. Suele corresponder a propiedades o conceptos intangibles, abstractos o complejos que no se manifiestan de forma directa.
Por ejemplo: Inteligencia, Felicidad, Inflación, PIB.
Guillermo Briones en Metodología de la investigación cuantitativa en las ciencias sociales dice:
“Un constructo es una propiedad que se supone posee una persona, la cual permite explicar su conducta en determinadas ocasiones. Como tal, el constructo es un concepto teórico, hipotético. Por ejemplo, la inteligencia, la motivación, la creatividad, las actitudes, etc.
Por su lado, las variables son propiedades, características o atributos que se dan en grados o modalidades diferentes en las personas y, por derivación de ellas, en los grupos o categorías sociales. Así, son variables, la edad, el ingreso, la educación, el sexo, la ocupación, etc., que, como se ve, corresponden a grados diferentes o iguales de darse una cierta propiedad en las personas o de darse en modalidades diferentes.
Los constructos se definen como propiedades subyacentes, que no pueden medirse en forma directa, sino mediante manifestaciones externas de su existencia, es decir, mediante indicadores. En otras palabras, los constructos son variables subyacentes, por lo cual, habitualmente, caen en la denominación común de variables.”
1.1.4 Ramas o áreas iniciales
Estadística descriptiva: Describir, presentar, resumir un conjunto de datos.
Estadística inferencial: Sacar conclusiones sobre la población a partir de lo que se observa en la muestra (toma de decisión, predicción, conclusiones).
Probabilidad: Formalización matemática que busca definir y medir la incertidumbre (aleatoriedad).
Dependiendo del número de variables de interés también se habla de estadística univariada, bivariada o multivariada.
1.1.5 Relación entre los conceptos
1.2 Clasificación de variables
Variable cualitativa o categórica: Los valores que toma la variable describen un atributo o característica de los individuos (los valores NO tienen un sentido numérico).
Variable cuantitativa o numérica: Los valores que toma la variable cuantifican o miden un atributo o característica de los individuos (los valores tienen un sentido numérico).
flowchart LR A(Clasificar en:) --> D(Cualitativa o categórica) A --> E(Cuantitativa o numérica)
Ejercicio 1.1 Un grupo de investigadores desea aplicar una encuesta para caracterizar a los estudiantes de una universidad. A continuación se describen algunas variables incluidas en el formulario. Para cada una identifique si la variable es cualitativa o cuantitativa.
- Color favorito declarado por el estudiante
- Número de hermanos del estudiante
- Marca de teléfono móvil que utiliza el estudiante
- Altura del estudiante en metros
- Estrato socioeconómico del estudiante
- Estado civil actual del estudiante
¿Alguna de las anteriores variables podría clasificarse de manera diferente si cambiara el contexto o la forma en que se solicitan los datos? ¿Puede dar un ejemplo concreto en el que la clasificación de una variable cambie debido por ejemplo al contexto?
La clasificación (y la escala de medida) de una variable depende principalmente del objetivo del estudio o análisis, de su contexto, y de la manera en que se espera tener los datos para dicha variable.
1.3 Escalas de medida
La escala de medida de una variable determina las “posibilidades operativas o matemáticas” de los valores que ésta toma; Por ende, también determinará qué tratamiento y qué tipo de análisis serían los adecuados para la respectiva variable.
flowchart LR A(Clasificar en:) --> B(Cualitativa o categórica) A --> C(Cuantitativa o numérica) B --> B1(Nominal) B --> B2(Ordinal) C --> C1(De intervalo) C --> C2(De razón)
Nominal: Los valores que toma la variable son descriptivos, es decir, etiquetas o nombres. Lo único que se puede hacer es clasificar o agrupar los individuos de acuerdo al valor que toma la variable para cada uno.
Por ejemplo:
- Género (F, M).
- Grupo sanguíneo (A, B, AB, O).
- Color de cabello (aunque puede que no en todos los casos).
Ordinal: Los valores que toma la variable son descriptivos, es decir, etiquetas o nombres pero estos, además de permitir clasificar, tienen una relación de orden.
Por ejemplo:
- Estrato Socioeconómico (1, 2, 3, …, 6).
- Nivel de Inglés CEF (A1, A2, B1, B2, C1, C2).
- Escala Likert (p.ej: Totalmente en desacuerdo, En desacuerdo, Ni de acuerdo ni en desacuerdo, De acuerdo, Totalmente de acuerdo).
De intervalo: Incluye las características de una variable con escala de medida ordinal, pero adicionalmente tiene sentido tanto la suma como la resta de valores (las distancias entre los valores tienen sentido).
Por ejemplo:
- Número de hijos.
- Número de estudiantes.
- Número de materias.
De razón: Incluye las características de una variable con escala de medida de intervalo, pero adicionalmente tienen sentido la multiplicación y división de valores de la variable (la razón entre los valores tiene sentido) y el valor cero representa la ausencia de lo que mide la variable (el cero es significativo).
Por ejemplo:
- Tiempo en horas, minutos, segundos, etc.
- Medidas físicas como longitud, peso, área, etc.
- Cantidades en unidades monetarias como ingresos, tasa de cambio, etc.
En conclusión, las “posibilidades operativas o matemáticas” de cada escala de medida se resumen en la siguiente tabla:
| Escalas de medida | =, \neq | <, \leq, >, \geq | +, - | \times, \div, 0 |
|---|---|---|---|---|
| Nominal | \checkmark | |||
| Ordinal | \checkmark | \checkmark | ||
| De intervalo | \checkmark | \checkmark | \checkmark | |
| De razón | \checkmark | \checkmark | \checkmark | \checkmark |
- Identifica o selecciona al menos una variable de cada escala de medida, que sea de tu interés (a nivel personal o para tu carrera). Estas variables de interés serán vinculadas o relacionadas con los ejemplos que haga en clase, razón por la cual es importante que las tengas por escrito y las traigas a todas las clases del semestre.
- No olvides seleccionar y resolver ejercicios de un libro acerca de lo visto en esta sección (preferiblemente que tengan respuesta). Por ejemplo, resuelve los ejercicios 1.1, 1.2 y 1.5 a 1.9 del libro: Introducción a la Probabilidad y Estadística. William Mendenhall, Robert J. Beaver and Barbara M. Beaver (2010). (13a Ed.) Cengage Learning.