11  Distribuciones muestrales

En esta sección se hará una revisión de algunos aspectos relacionados con las distribuciones de estadísticos que relacionan un parámetro de interés (\theta) con su respectivo estimador puntual (T).

Actividad autónoma Independiente (antes de clase)

• Lea todo el contenido de la presente sección (Inferencia, 11. Distribuciones muestrales).

En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.

Dado el alcance de este material, solamente se considerarán las siguientes seis situaciones, que a su vez se dividen en dos escenarios posibles.

• Tenemos un parámetro de interés de una sola población:

  • Media: T = \bar{X} es un estimador puntual de \theta = \mu.
  • Proporción: T = \hat{P} es un estimador puntual de \theta = p.
  • Varianza (y/o desviación estándar): T = S^2 es un estimador puntual de \theta = \sigma^2.

• Tenemos un parámetro de interés compuesto que relaciona un mismo parámetro de cada una de dos poblaciones distintas:

  • Medias: T = \bar{X_1} - \bar{X_2} es un estimador puntual de \theta = \mu_1 - \mu_2.
  • Proporciones: T = \hat{P_1} - \hat{P_2} es un estimador puntual de \theta = p_1 - p_2.
  • Varianzas (y/o desviaciones estándar): T = \frac{S_1^2}{S_2^2} es un estimador puntual de \theta = \frac{\sigma_1^2}{\sigma_2^2}.

En el siguiente enlace encontrarán un archivo .pdf con el resumen de las fórmulas asociadas a las secciones: “Distribuciones muestrales”, “Estimación por intervalo” y “Juzgamiento”: ResumenFormulasInferencia.pdf

11.1 Preliminares

11.1.1 Teorema del Límite Central

Ejercicio 11.1 Teniendo en cuenta los diez resultados que obtuvo al lanzar una moneda 10 veces consecutivas (es decir, la realización de la muestra aleatoria de tamaño 10 que usted obtuvo).

• Suponga que todos los estudiantes hacen el ejercicio con la misma moneda, ¿todos obtienen la misma estimación? ¿por qué?
• Si tomo todas las estimaciones y con ellas hago un histograma ¿qué forma tendría?
• ¿Cuál sería la distribución teórica de todas las estimaciones posibles (de todas las posibles muestras posibles de tamaño 10)?

Si \bar{X} es la media de una muestra aleatoria de tamaño n tomada de una población con media \mu y varianza finita \sigma^2, entonces, cuando n \to \infty, la distribución de Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} tiende a una normal estándar. Escrito de otra manera, \bar{X} \underset{n \to \infty}{\longrightarrow} W \sim \mathcal{N}\left(\mu, \frac{\sigma}{\sqrt{n}} \right) o lo que es lo mismo (estandarizando), \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \underset{n \to \infty}{\longrightarrow} Z \sim \mathcal{N}\left(0,1\right)

Tenga en cuenta que:

• La aproximación en varios casos será buena para n \geq 30.

• Para n < 30, la aproximación es buena solamente si la distribución es cercana a la normal.

• Si la distribución de la población es una normal, entonces, para cualquier valor de n, la distribución de \bar{X} es exactamente una normal.

Para ilustrar lo anterior:

• Sampling Distribution of the Sample Proportion

• Sampling Distribution of the Sample Mean. Discrete Population Distribution

• Sampling Distribution of the Sample Mean. Continuous Population Distribution

Ejercicio 11.2  

Las estaturas de 1000 estudiantes se distribuyen aproximadamente de forma normal con una media de 174.5 centímetros y una desviación estándar de 6.9 centímetros. Si se extraen 200 muestras aleatorias de tamaño 25 de esta población y las medias se registran al décimo de centímetro más cercano, determine:

1. la media y la desviación estándar de la distribución muestral de \bar{X};
2. el número de las medias muestrales que caen entre 172.5 y 175.8 centímetros;
3. el número de medias muestrales que caen por debajo de 172.0 centímetros.

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 8. Ejercicio 22.

11.1.2 Distribuciones adicionales requeridas

11.1.2.1 Distribución Ji/Chi-cuadrado

Si Z_1 \sim \mathcal{N}(0,1), \dots, Z_\nu \sim \mathcal{N}(0,1) entonces \sum_{i=1}^{\nu} Z_i^2 \sim \chi^2_\nu \Big(\Big.Si Z_1, \dots, Z_\nu son variables aleatorias normales estándar independientes, entonces la variable aleatoria \sum_{i=1}^{\nu} Z_i^2 es chi-cuadrado de parámetro \nu.\Big.\Big)

Efecto de los parámetros

https://cjtorresj.shinyapps.io/introChiSqDistribution/

11.1.2.2 Distribución t de Student

Si Z \sim \mathcal{N}(0,1) y V \sim \chi^2_\nu son independiente, entonces, \frac{Z}{\sqrt{V/\nu}} \sim t_\nu \Big(\Big.Si Z es una variable aleatoria normal estándar, V es una variable aleatoria chi-cuadrado con \nu grados de libertad, y Z y V son independientes, entonces la variable aleatoria \frac{Z}{\sqrt{V/\nu}} es t de Student con \nu grados de libertad.\Big.\Big)

Efecto de los parámetros

https://cjtorresj.shinyapps.io/introtDistribution/

11.1.2.3 Distribución F de Fisher-Snedecor

Si U \sim \chi^2_{\nu_1} y V \sim \chi^2_{\nu_2} son independientes, entonces, \frac{U/\nu_1}{V/\nu_2} \sim f_{\nu_1,\nu_2} \Big(\Big.Si U es una variable aleatoria chi-cuadrado con \nu_1 grados de libertad, V es una variable aleatoria chi-cuadrado con \nu_2 grados de libertad, y U y V son independientes, entonces la variable aleatoria \frac{U/\nu_1}{V/\nu_2} es F de Fisher con \nu_1 grados de libertad en el numerador y \nu_2 grados de libertad en el denominador.\Big.\Big)

Efecto de los parámetros

https://cjtorresj.shinyapps.io/introFDistribution/

En el Apéndice D hay una pequeña y rápida revisión de algunas características de las distribuciones: ji/chi cuadrado, t de Student y F de Fisher-Snedecor (Distribuciones adicionales requeridas)

11.1.3 Notación

Considere los valores z_{(\alpha)}, t_{(\alpha,\nu)}, \chi^2_{(\alpha,\nu)} y f_{(\alpha,\nu_1,\nu_2)} tal que:

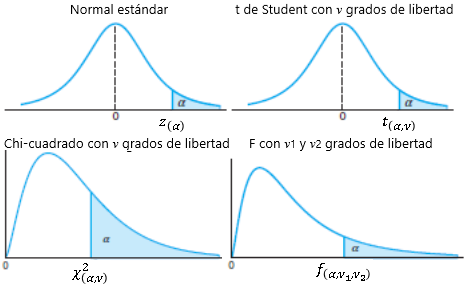
Note la relación entre la notación que hemos estado utilizando para los cuantiles y esta nueva notación para todo lo que viene de aquí en adelante en el tema de inferencia (mi intención es tener una pequeña variante en la notación que permita diferenciar y no confundir una cosa con otra):

\begin{aligned} z_{1 - \alpha} &= z_{(\alpha)} \\ t_{1-\alpha,\nu} &= t_{(\alpha,\nu)} \\ \chi^2_{1-\alpha,\nu} &= \chi^2_{(\alpha,\nu)} \\ f_{1-\alpha,\nu_1,\nu_2} &= f_{(\alpha,\nu_1,\nu_2)} \end{aligned}

En adelante todos los resultados expuestos supondrán que n es suficientemente grande (para poder aplicar el Teorema del Límite Central) o que la población tiene una distribución normal o muy cercana (para poder utilizar las distribuciones t de Student, Chi-cuadrado y F de Fisher-Snedecor).

11.2 Una población

11.2.1 Media

En el caso de la media de una población, sabemos que T = \bar{X} es un estimador puntual de \theta = \mu. Además, bajo diferentes supuestos, tenemos los siguientes dos resultados para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

1. Si \sigma es conocida, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de la población tiene distribución normal tenemos que,

   \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim \mathcal{N}(0,1)

2. Si \sigma es desconocida, entonces, bajo el supuesto de que la variable de interés de la población tiene distribución normal tenemos que,

   \frac{\bar{X} - \mu}{S/\sqrt{n}} \sim t_{n-1}

Ejercicio 11.3  

Después de deducir los gastos necesarios, el costo promedio por asistir a la Universidad del Sur de California (USC) es de \$27175 (U. S. News & World Report, America’s Best Colleges, ed. 2009). Suponga que la desviación estándar poblacional es \$7400. Asuma que se selecciona una muestra aleatoria de 60 estudiantes de la USC de esta población.

1. ¿Cuál es el valor esperado de la media muestral en este estudio?
2. ¿Cuál es el valor del error estándar?
3. ¿Cuál es la distribución de muestreo? ¿Qué indica esta distribución?
4. ¿Cuál es la probabilidad de que la media muestral sea mayor que \$27175?
5. ¿Cuál es la probabilidad de que la media muestral no se aleje más o menos de \$1000 de la media poblacional?
6. ¿Qué tanto variaría la probabilidad del inciso anterior si el tamaño de la muestra se aumentara a 100?

Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio complementario 46.

Ejercicio 11.4  

Un inspector de control de calidad vigila periódicamente un proceso de producción. El inspector selecciona muestras aleatorias simples de 30 artículos ya terminados y calcula la media muestral del peso del producto \bar{x}. Si en un periodo largo se encuentra que 5\% de los valores de \bar{x} son mayores que 2.1 libras y 5\% son menores que 1.9 libras, ¿cuáles son la media y la desviación estándar de la población de los productos elaborados en este proceso?

Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio complementario 49.

11.2.2 Proporción

En el caso de la proporción de una población, sabemos que T = \hat{P} es un estimador puntual de \theta = p. Además, para n suficientemente grande (np > 10 y n(1-p) > 10), tenemos el siguiente resultado para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

\frac{\hat{P} - p}{\sqrt{\frac{p(1-p)}{n}}} \sim \mathcal{N}(0,1)

Ejercicio 11.5  

Los publicistas contratan a proveedores de servicios de Internet y motores de búsqueda para colocar sus anuncios en los sitios web. Pagan una cuota con base en el número de clientes potenciales que hacen clic en su publicidad. Desafortunadamente, el fraude por clic (la práctica de hacer clic en una publicidad con el solo objeto de aumentar las ganancias) se ha convertido en un problema. El 40\% de los anunciantes se queja de haber sido víctima de fraude por clic (BusinessWeek, 13 de marzo de 2006). Suponga que se toma una muestra aleatoria de 380 publicistas con objeto de aprender más acerca de cómo son afectados por esta práctica.

1. ¿Cuál es el valor esperado de la proporción muestral en este estudio?
2. ¿Cuál es el error estándar?
3. ¿Cuál es la distribución de muestreo? ¿Qué indica esta distribución?
4. ¿Cuál es la probabilidad de que la proporción muestral sea mayor que 0.45?
5. ¿Cuál es la probabilidad de que la proporción muestral esté a no más de \pm 0.04 de la proporción poblacional que ha experimentado fraude por clic?

Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio complementario 52.

11.2.3 Varianza

En el caso de la varianza (y/o desviación estándar) de una población, sabemos que T = S^2 es un estimador puntual de \theta = \sigma^2. Además, bajo el supuesto de que la variable de interés de la población tiene distribución normal, tenemos el siguiente resultado para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}

Ejercicio 11.6  

Suponga que las varianzas muestrales son mediciones continuas. Calcule la probabilidad de que una muestra aleatoria de 25 observaciones, de una población normal con varianza \sigma^2 = 6, tenga una varianza muestral S^2

1. mayor que 9.1;
2. entre 3.462 y 10.745.

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 8.41.

11.3 Dos poblaciones

11.3.1 Medias

En el caso de las medias de dos poblaciones, sabemos que T = \bar{X_1} - \bar{X_2} es un estimador puntual de \theta = \mu_1 - \mu_2. Además, bajo diferentes supuestos, tenemos los siguientes cuatro resultados para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

1. Si son observaciones pareadas, entonces haga:

   X = X_1 - X_2 lo que implica que \bar{X} = \bar{X}_1 - \bar{X}_2 y \mu = \mu_1 - \mu_2, quedando así en la situación de una media de una población (para los anteriores X, \bar{X} y \mu).

2. Si NO son observaciones pareadas, con \sigma_1 y \sigma_2 conocidas, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,

   \frac{ \left( \bar{X}_1 - \bar{X}_2 \right) - \left( \mu_1 - \mu_2 \right)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim \mathcal{N}(0,1)

3. Si NO son observaciones pareadas y se considera que \sigma_1 = \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,

   \frac{ \left( \bar{X}_1 - \bar{X}_2 \right) - \left( \mu_1 - \mu_2 \right)}{S_p \, \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t_{n_1+n_2-2} donde S_p^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1+n_2-2}

4. Si NO son observaciones pareadas y se considera que \sigma_1 \neq \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,

   \frac{ \left( \bar{X}_1 - \bar{X}_2 \right) - \left( \mu_1 - \mu_2 \right)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} \sim t_{\nu} donde, \nu = \left\lfloor \frac{\left(S_1^2/n_1+S_2^2/n_2\right)^2}{\frac{\left(S_1^2/n_1\right)^2}{n_1-1} + \frac{\left(S_2^2/n_2\right)^2}{n_2-1}} \right\rfloor

11.3.2 Proporciones

En el caso de las proporciones de dos poblaciones, sabemos que T = \hat{P_1} - \hat{P_2} es un estimador puntual de \theta = p_1 - p_2. Además, bajo diferentes supuestos, tenemos los siguientes tres resultados para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

1. Si son observaciones pareadas, entonces haga

   X = X_1 - X_2 lo que implica que \bar{X} = \hat{P}_1 - \hat{P}_2 y \mu = p_1 - p_2, quedando así en la situación de una media de una población (para los anteriores X, \bar{X} y \mu).

2. Si NO son observaciones pareadas y se considera que p_1 = p_2, entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right) se tiene que,

   \frac{ \left( \hat{P}_1 - \hat{P}_2 \right) - \left( 0 \right)}{ \sqrt{\hat{P} (1-\hat{P}) \, \left(\frac{1}{n_1}+\frac{1}{n_2}\right)}} \sim \mathcal{N}(0,1) donde, \hat{P} = \frac{n_1 \hat{P}_1 + n_2 \hat{P}_2}{n_1 + n_2}

3. Si NO son observaciones pareadas y se considera que p_1 \neq p_2, entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right) se tiene que,

   \frac{ \left( \hat{P}_1 - \hat{P}_2 \right) - \left( p_1 - p_2 \right)}{\sqrt{\frac{\hat{P}_1\left(1-\hat{P}_1\right)}{n_1}+\frac{\hat{P}_2\left(1-\hat{P}_2\right)}{n_2}}} \sim \mathcal{N}(0,1)

11.3.3 Varianzas

En el caso de las varianzas (y/o desviaciones estándar) de dos poblaciones, sabemos que T = \frac{S_1^2}{S_2^2} es un estimador puntual de \theta = \frac{\sigma_1^2}{\sigma_2^2}. Además, bajo el supuesto de que la variable de interés de cada población tiene distribución normal (X_1 y X_2), tenemos el siguiente resultado para un estadístico que relaciona dicho parámetro de interés (\theta) con su respectivo estimador puntual (T).

\frac{\frac{S_1^2}{\sigma_1^2}}{\frac{S_2^2}{\sigma_2^2}} = \frac{S_1^2 \sigma_2^2}{S_2^2 \sigma_1^2} \sim F_{n_1-1,n_2-1}

Ejercicio 11.7  

Si S_1^2 y S_2^2 representan las varianzas de muestras aleatorias independientes de tamaños n_1 = 25 y n_2 = 31, tomadas de poblaciones normales con varianzas \sigma_1^2 = 10 y \sigma_2^2 = 15, respectivamente, calcule P\left[\frac{S^2_1}{S^2_2} < 1.26\right].

Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 8.59.

Actividad autónoma Independiente (después de clase)

• No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios del capítulo 8 (sin las secciones 8.1 y 8.8) del libro de Walpole o del capítulo 7 (solamente los ejercicios asociados a las secciones 7.5 y 7.6) del libro de Anderson.