8 Distribuciones continuas
En esta sección se hará una revisión de algunos “grupos particulares” de variables aleatorias continuas, también llamados modelos probabilísticos continuas o distribuciones continuas, como lo son: la uniforme continua, la exponencial y la gaussiana/normal.
- Lee todo el contenido de esta sección (Probabilidad, 8 Distribuciones continuas).
- En tus propias palabras, has una exposición escrita detallada en tu cuaderno sobre cada parte de lo leído, como si le estuvieras explicando a un compañero o amigo. Recuerda que aprendemos aproximadamente el 95% de lo que tratamos de enseñar a otros.
- Anota cualquier duda o tema que te resulte confuso. ¡No te preocupes si no lo entiendes todo a la primera!
- Busca por tu cuenta respuestas a esas dudas. Esto te ayudará a llegar a clase con ideas para compartir.
- Lleva a clase: tu exposición escrita, tus dudas y las respuestas que encontraste. ¡Trabajaremos juntos para aclararlo todo!
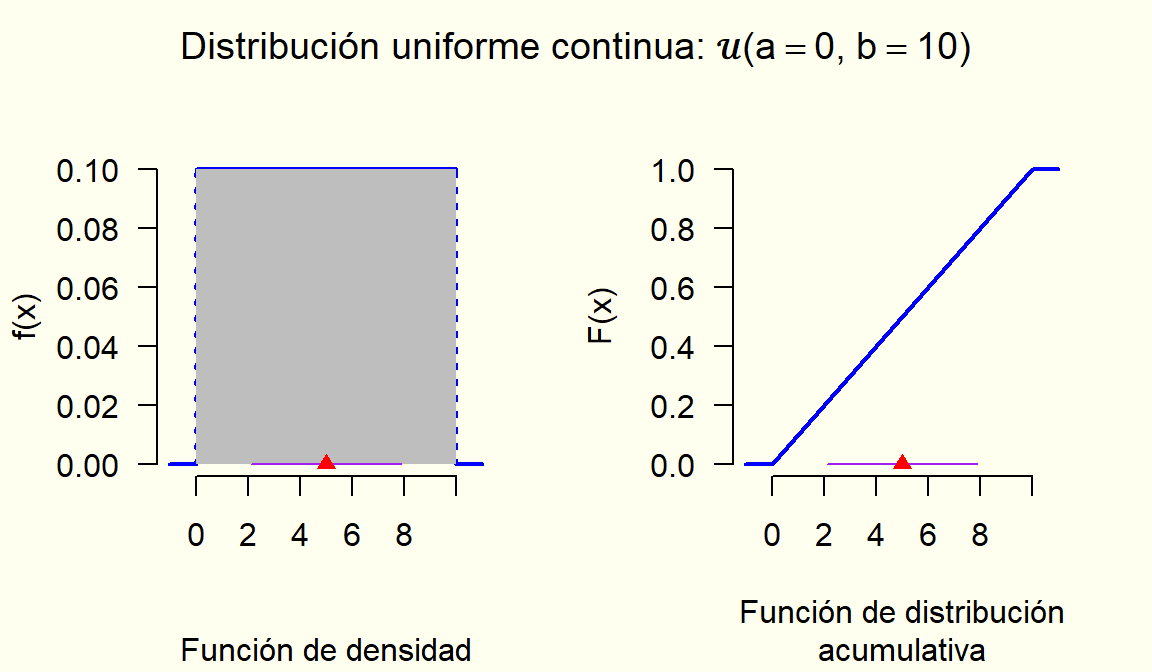
8.1 Uniforme Continua
Situaciones en donde podría aplicar:
Cuando la variable puede tomar valores entre un valor mínimo y un valor máximo, sin que haya una parte del intervalo para la cual los valores sean más probables o menos probables que para el resto de partes del intervalo, es decir, “la probabilidad se reparte exactamente igual o equitativamente a lo largo de todo el intervalo”.
Es la distribución más simple para una variable continua que solamente puede tomar valores en un intervalo doblemente acotado.
Ejercicio 8.1
Un autobús llega cada 10 minutos a una parada. Se supone que el tiempo de espera para un individuo en particular es una variable aleatoria con distribución continua uniforme.
¿Cuál es la probabilidad de que el individuo espere más de 7 minutos?
¿Cuál es la probabilidad de que el individuo espere entre 2 y 7 minutos?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 6.4.
Características:
Extiende, al caso continuo, la idea de que todos los valores de la variable aleatoria X son igualmente probables.
Valores que puede tomar la variable aleatoria:
x \in [a,b].
Parámetros:
a, valor mínimo que puede tomar la variable aleatoria, y b, valor máximo que puede tomar la variable a aleatoria. -\infty < a < b < \infty
Notación:
X \sim \mathcal{U}(a,b), esto se lee así: la variable aleatoria X tiene una distribución uniforme continua de parámetros a y b.
Función de densidad:
f_X(x) = \begin{cases} \frac{1}{b-a} & \text{Si } a < x < b \\ 0 & \text{en otro caso} \end{cases}
Función de distribución acumulativa:
F_X(x) = \begin{cases} 0 & \text{Si } x < a \\ \frac{x-a}{b-a} & \text{Si } a \leq x < b \\ 1 & \text{Si } b \leq x \end{cases}
Valor esperado y varianza:
\mu_X = E[X] = \frac{a+b}{2}
\sigma_X^2 = Var[X] = \frac{(b-a)^2}{12}
Ejercicio 8.2 Supongamos que el tiempo de desplazamiento en TM de mi casa a la Universidad puede ser cualquier valor entre 40 y 60 minutos, todos igualmente probables. Si a las 10:05 am estoy tomando el TM desde la estación que queda cerca a mi casa, ¿cuál es la probabilidad de que llegue tarde a clase de 11 am?, ¿En promedio a que horas se espera que llegue?
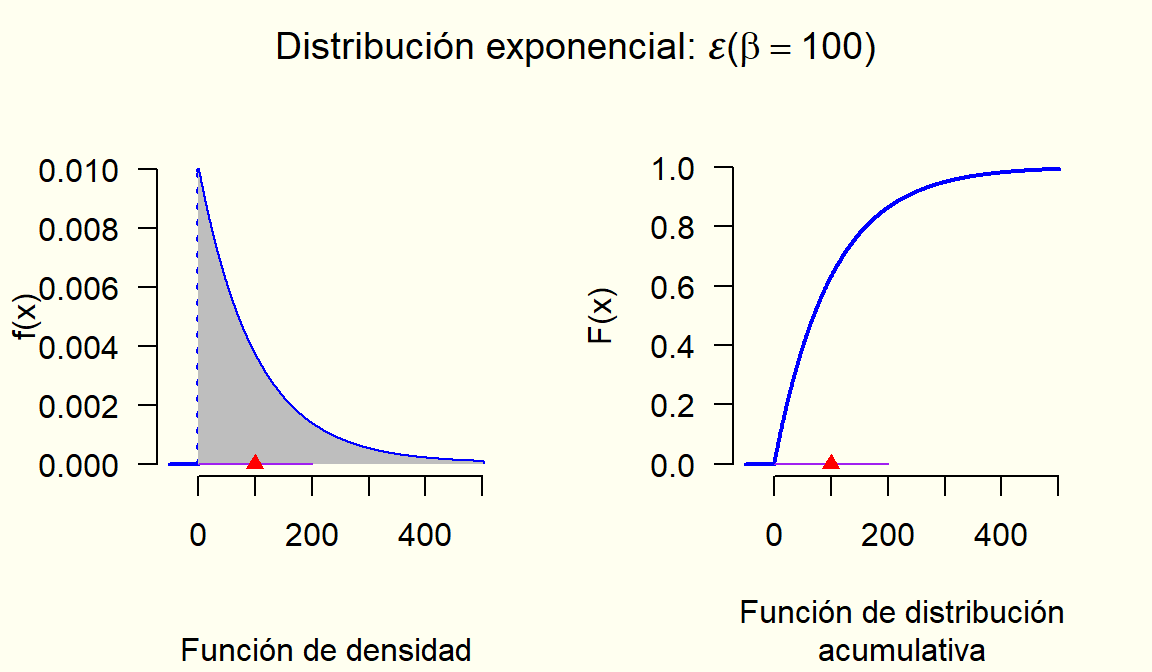
8.2 Distribución Exponencial
Algunas situaciones en donde podría aplicar:
Se utiliza comúnmente en diversas situaciones en las que se modela el tiempo entre situaciones sucesivas que ocurren de forma independiente a una tasa constante. (por ejemplo, tiempo transcurrido entre contratos aprobados, o ataques informáticos, o clientes que llegan, o entre llamadas recibidas, etc.)
También serviría para modelar distancia entre ocurrencias consecutivas (por ejemplo, distancia entre huecos consecutivos en una vía).
Puede ser la distribución continua más simple para modelar una variable continua que no puede tomar valores negativos.
Ejercicio 8.3
Cierto tipo de dispositivo tiene una tasa de fallas anunciada de 0.01 por hora. La tasa de fallas es constante y se aplica la distribución exponencial.
¿Cuál es el tiempo promedio que transcurre antes de la falla?
¿Cuál es la probabilidad de que pasen 200 horas antes de que se observe una falla?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 6.66.
Características:
La longitud de intervalo entre ocurrencias consecutivas de un proceso Poisson es una variable aleatoria X con distribución exponencial.
Si Y := “número de ocurrencias” y Y \sim \mathcal{P}(\lambda), entonces X := “longitud de intervalo entre ocurrencias” tiene distribución exponencial de parámetro de escala \beta = \frac{1}{\lambda} o de parámetro de tasa \lambda.
Valores que puede tomar la variable aleatoria:
Los números reales positivos (x > 0) o los no negativos (x \geq 0).
Parámetros:
Promedio de la variable \left(\beta\right) (parámetro de escala), es decir, tiempo o distancia promedio entre ocurrencias consecutivas; o promedio de ocurrencias por unidad de medida de la variable \left(\lambda = \frac{1}{\beta}\right).
Notación:
X \sim \mathcal{E}(\beta), esto se lee así: la variable aleatoria X tiene una distribución exponencial de parámetro (de escala) \beta; o X \sim \mathcal{E}(\lambda), esto se lee así: la variable aleatoria X tiene una distribución exponencial de parámetro (de tasa) \lambda.
Función de densidad:
\begin{aligned} f_X(x) &= \begin{cases} \frac{1}{\beta} e^{-x/\beta} & \text{Si } x \geq 0 \\ 0 & \text{en otro caso} \end{cases} \\ &= \begin{cases} \lambda e^{-\lambda \, x} & \text{Si } x > 0 \\ 0 & \text{en otro caso} \end{cases} \end{aligned}
Función de distribución:
\begin{aligned} F_X(x) &= \begin{cases} 0 & \text{Si } x < 0 \\ 1 - e^{-x/\beta} & \text{Si } 0 \leq x \end{cases} \\ &= \begin{cases} 0 & \text{Si } x < 0 \\ 1 - e^{-\lambda \, x} & \text{Si } 0 \leq x \end{cases} \end{aligned}
Valor esperado y varianza:
\mu_X = E[X] = \beta = \frac{1}{\lambda}
\sigma_X^2 = Var[X] = \beta^2 = \frac{1}{\lambda^2}
Adicionalmente consultar:
Exponential Distribution Applet/Calculator (permite dar cualquiera de los dos parámetros)
En una hoja de cálculo:
DISTR.EXP.N(x; lambda; acum)(sólo con parámetro de tasa)
Ejercicio 8.4 Supongamos que un estudiante siempre llega tarde a clase, que la cantidad de tiempo de clase que se pierde sigue una distribución exponencial y que su promedio de llegada tarde es de 10 minutos, ¿cuál es la probabilidad de que llegue a clase después de las 11:15 am?. Si después de llegar media hora tarde decide no entrar. ¿De 32 clases al semestre, a cuántas se esperaría que no entre?
8.3 Distribución Gaussiana
Características y algunas situaciones en donde podría aplicar:
“La distribución normal, distribución de Gauss, distribución gaussiana o distribución de Laplace-Gauss, es una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en estadística y en la teoría de probabilidades.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos.”
“Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
- caracteres morfológicos de individuos como la estatura;
- caracteres fisiológicos como el efecto de un fármaco;
- caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
- caracteres psicológicos como el cociente intelectual;
- nivel de ruido en telecomunicaciones;
- errores cometidos al medir ciertas magnitudes;
- etc.
La distribución normal también aparece en muchas áreas de la propia estadística.”

Valores que puede tomar la variable aleatoria:
Todos los números reales (x \in \mathbb{R}) (pero con probabilidad cada vez más baja, e incluso casi cero, para los valores que se encuentra cada vez relativamente más lejos de la media).
Parámetros:
Media de la variable aleatoria \left( \mu \in \mathbb{R} \right) y desviación estándar de la variable a aleatoria \left( \sigma > 0 \right).
¿Qué efecto tiene cada uno de los parámetros de la distribución gaussiana?
Notación:
X \sim \mathcal{N}(\mu,\sigma), esto se lee así: la variable X tiene una distribución normal de parámetros \mu (localización) y \sigma (escala).
Valor esperado y varianza:
\mu_X = E[X] = \mu
\sigma_X^2 = Var[X] = \sigma^2
Función de densidad:
f_X(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2} \left(\frac{x - \mu}{\sigma}\right)^2}
Función de distribución acumulativa:
\begin{aligned} F_X(x) &= \int_{-\infty}^{x} f_X(t) \, dt \\ &= \int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{1}{2} \left(\frac{t - \mu}{\sigma}\right)^2} \, dt \end{aligned}
Note que la función de distribución acumulativa de una variable aleatoria gaussiana simplemente se dejó expresada y ya. Resulta que no se conoce una expresión cerrada simple para la antiderivada de la función de densidad de una variable aleatoria gaussiana. Entonces, ¿cómo se supone que voy a obtener las probabilidades que necesito, si la integral correspondiente no tiene solución analítica?, recordemos que para una variable aleatoria continua: P[x_1 < X < x_2] = \int\limits_{x_1}^{x_2} f_X(t) \, dt.
La solución a la anterior inquietud sería la siguiente: para una variables aleatoria X \sim \mathcal{N}(\mu,\sigma), transformamos el problema P[x_1 < X < x_2] en un problema equivalente que use una variable aleatoria Z \sim \mathcal{N}(0,1), luego, usando aproximaciones numéricas de F_Z(z) = \int\limits_{-\infty}^{z} f_Z(t) \, dt, encontramos la respuesta al problema equivalente.
Transformación (Estandarización):
Si X \sim \mathcal{N}(\mu,\sigma) y Z = \frac{X-\mu}{\sigma}, entonces Z \sim \mathcal{N}(0,1).
\begin{aligned} P[x_1 < X < x_2] &= P\left[x_1 - \mu < X - \mu < x_2 - \mu\right] \\ &= P\left[\frac{x_1 - \mu}{\sigma} < \frac{X - \mu}{\sigma} < \frac{x_2 - \mu}{\sigma}\right] \\ &= P\left[z_1 < Z < z_2\right], \end{aligned} en donde, z_1 = \frac{x_1 - \mu}{\sigma} \quad \text{y} \quad z_2 = \frac{x_2 - \mu}{\sigma}, además ya sabíamos que, \begin{aligned} P\left[z_1 < Z < z_2\right] &= P\left[Z < z_2\right] - P\left[Z < z_1\right] \\ &= F_Z\left(z_2\right) - F_Z\left(z_1\right), \end{aligned} y las aproximaciones numéricas para F_Z(z) se encuentran tabuladas (por ejemplo, ver libro de Anderson. Página FM1 o 978) o se pueden obtener mediante herramientas computacionales, incluyendo algunas calculadoras.
Dentro del conjunto de variables aleatorias que tienen distribución gaussiana, Z \sim \mathcal{N}(0,1) es evidentemente una variable particularmente especial. Este caso especial se denomina distribución normal estándar (con media igual a cero y desviación estándar igual a uno) y naturalmente su función de densidad es, f_Z(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}
Una tabla de aproximaciones numéricas para F_Z(z):
| 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
Adicionalmente consultar:
Normal Distribution Applet/Calculator (para obtener probabilidad y cuantiles)
-
En una hoja de cálculo:
- Para obtener probabilidades:
DISTR.NORM.N(x; media; desv_estándar; acum)yDISTR.NORM.ESTAND.N(z; acumulado) - Para obtener cuantiles:
INV.NORM(probabilidad; media; desv_estándar)yINV.NORM.ESTAND(probabilidad)
- Para obtener probabilidades:
8.3.1 Ejercicios
Ejercicio 8.5
Dada una distribución normal con \mu = 30 y \sigma = 6, calcule
el área de la curva normal a la derecha de x = 17;
el área de la curva normal a la izquierda de x = 22;
el área de la curva normal entre x = 32 y x = 41;
el valor de x que tiene 80% del área de la curva normal a la izquierda;
los dos valores de x que contienen 75% central del área de la curva normal.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 6.8.
Ejercicio 8.6
Dada la variable X normalmente distribuida con una media de 18 y una desviación estándar de 2.5, calcule
P(X < 15);
el valor de k tal que P(X < k) = 0.2236;
el valor de k tal que P(X > k) = 0.1814;
P(17 < X < 21).
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 6.9.
Ejercicio 8.7 Supongamos que el tiempo de desplazamiento en TM de mi casa a la Universidad tiene una distribución normal con media 50 minutos y desviación estándar 5 minutos. Si a las 10:05 am estoy tomando el TM desde la estación cerca de mi casa, ¿cuál es la probabilidad de que llegue tarde a clase de 11 am?. ¿De 32 clases, a cuántas se espera que llegue tarde?
Ejercicio 8.8
El precio medio de las acciones de las empresas que forman el S&P 500 es \$30, y la desviación estándar es \$8.20 (BusinessWeek, publicación anual especial, primavera de 2003). Suponga que los precios de las acciones se distribuyen normalmente.
¿Cuál es la probabilidad de que las acciones de una empresa tengan un precio mínimo de \$40?
¿Cuál es la probabilidad de que el precio de las acciones no supere \$20?
¿Qué tan alto debe ser el precio de las acciones de una firma para situarla en el 10\% de las principales empresas?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Sección 6.2, ejercicio 18.
8.3.2 Regla empírica
Sea X \sim \mathcal{N}(\mu, \sigma), obtenga analíticamente el resultado para las siguientes probabilidades (no hay necesidad de reemplazar \mu y \sigma por valores numéricos):
P[\mu - \sigma < X < \mu + \sigma] = ¿?
P[\mu - 2 \, \sigma < X < \mu + 2 \, \sigma] = ¿?
P[\mu - 3 \, \sigma < X < \mu + 3 \, \sigma] = ¿?
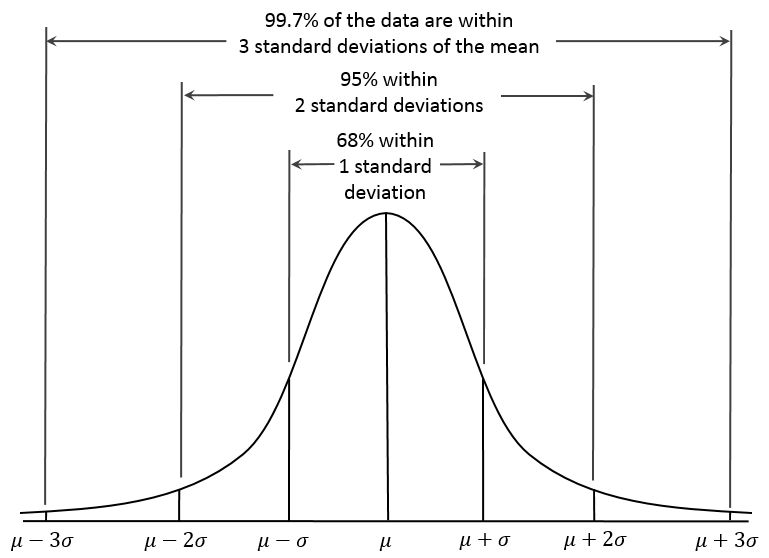
Supongamos que la estatura media de los hombres adultos en cierto país es de aproximadamente 177.8 cm, con una desviación estándar de alrededor de 7.62 cm. Sin conocer nada más (de la respectiva variable aleatoria), usando la desigualdad de Chebyshev, puedo asegurar que al menos (como mínimo) el 75\% de los hombres adultos de ese cierto país tienen una estatura entre 162.56 y 193.04 cm
Si asumo que la estatura tiene distribución gaussiana,
¿qué porcentaje de los hombres adultos de ese país tendrán una estatura entre 170.18 y 185.42 cm?
¿entre qué estaturas estaría el 95\% central de las estaturas de los hombres adultos de ese país?
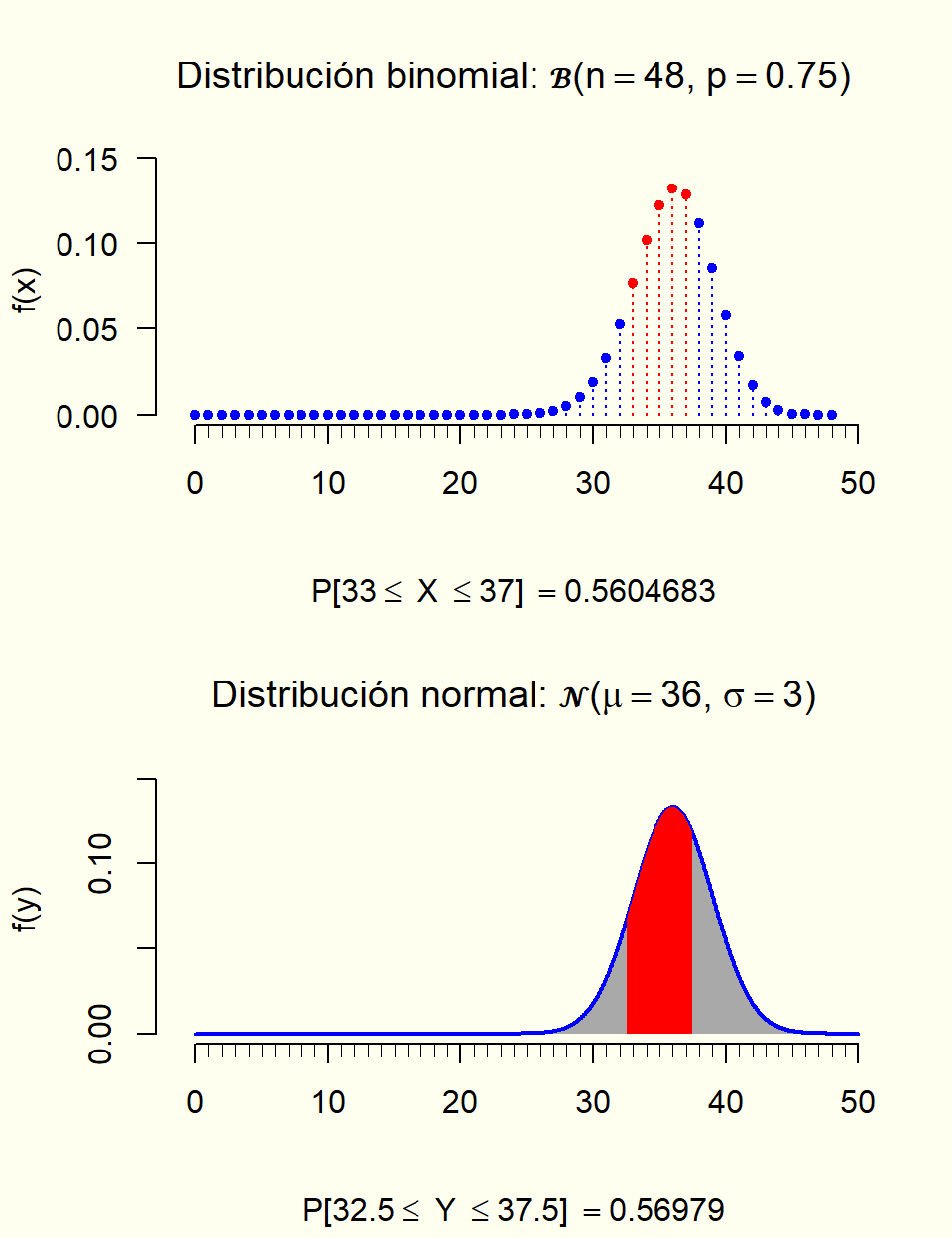
8.3.3 Relación con la binomial (Opcional)
Se tiene que, X \sim \mathcal{B}(n,p) \underset{n \to \infty}{\longrightarrow} Y \sim \mathcal{N}\left(np, \sqrt{np(1-p)}\right)
Es decir, si X \sim \mathcal{B}(n,p), entonces \frac{X - np}{\sqrt{np(1-p)}} \underset{n \to \infty}{\longrightarrow} Z \sim \mathcal{N}(0, 1)
Generalmente se debe hacer una corrección por continuidad (es decir, tengo que tener en cuenta que estoy utilizando una distribución continua para aproximar una distribución discreta):
Si X \sim \mathcal{B}(n,p), np > 5 y n(1-p) > 5 entonces,
\begin{aligned} P[X \leq x] &\approx P\left[Y \leq (x+0.5) \right] \\ & \approx P\left[Z \leq \frac{(x+0.5)-np}{\sqrt{np(1-p)}} \right] \end{aligned} donde Y \sim \mathcal{N}(np,\sqrt{np(1-p)}) y Z \sim \mathcal{N}(0,1).
Buscando ilustrar en alguna medida todo lo anterior, se presenta el siguiente gráfico:
Ejercicio 8.9 Se cree que 1 de cada 10 votantes registrados en una gran ciudad están a favor de un nuevo impuesto. Si se escogen de manera aleatoria e independiente 1000 votantes y se les pregunta su opinión, ¿cuál es la probabilidad de que al menos 900 estén en contra?
8.4 Adicionalmente (Opcional)
Para conocer la “forma” de las funciones de distribución y de masa de probabilidad / de densidad de algunas distribuciones discretas y continuas que no alcanzamos a mencionar en esta y en la anterior sección, pueden ir al siguiente enlace: Quantile App
Para complementar lo anterior, y para explorar la relación entre algunas distribuciones discretas y continuas, pueden consultar el siguiente enlace: Univariate Distribution Relationships
Para consultar la ayuda acerca de las distribuciones incorporadas en la instalación base del software estadístico R, dar la instrucción:
?distributions
- No olvides seleccionar y resolver ejercicios de un libro acerca de lo visto en esta sección (preferiblemente que tengan respuesta). Por ejemplo, selecciona ejercicios de las secciones 6.1 a 6.6 (sin incluir ejercicios de la distribución gamma en la sección 6.6) del libro de Walpole o del capítulo 6 del libro de Anderson.