5 Probabilidad condicional y relacionados
En esta sección se hará una revisión de algunos temas relacionados con probabilidad condicional, regla de multiplicación, probabilidad total, regla de Bayes e independencia.
- Lea todo el contenido de la presente sección (Probabilidad, 5 Probabilidad condicional y relacionados).
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
5.1 Probabilidad condicional
Antes de empezar, recuerde todo lo visto acerca de tablas de frecuencias absolutas, de frecuencias relativas, de perfiles fila y de perfilas columna.
Ejercicio 5.1
El director de planeación de Devine Dining, Inc., desea estudiar la relación entre el género de un huésped y el postre que ordena. Para investigar esta relación, el gerente recopiló la siguiente información.
Lind, Marchal & Wathen (2012). Estadistica Aplicada a los Negocios y la Economia. (15a. ed.) McGraw-Hill. Capítulo 4, Ejercicio 25.
| \, | Torta de chocolate | Tres leches | Tiramisú | TOTAL |
|---|---|---|---|---|
| Hombre | 32 | 26 | 11 | 69 |
| Mujer | 48 | 39 | 44 | 131 |
| TOTAL | 80 | 65 | 55 | 200 |
Si se selecciona un huésped al azar, ¿cuál es la probabilidad de que:
- sea hombre y ordenara Tres Leches?
- sea hombre o ordenara Tres Leches?
- sea hombre y no ordenara Tres Leches?
- ordenara Tres Leches, pero sabiendo que el huésped que ordenó el postre es hombre?
- sea hombre, pero sabiendo que el huésped ordenó Tres Leches?
Definición 5.1 (Probabilidad condicional) La probabilidad condicional de que ocurra el evento A dado que ocurrió el evento B, se define como,
\begin{aligned} P[A|B] := \frac{P[A \cap B]}{P[B]} \quad \text{para} \quad P[B]>0 \end{aligned}
Ejemplo 5.1 Ir a Conditional Probability Experiment
Ejercicio 5.2
Un grupo de estudiantes de física avanzada se compone de 10 alumnos de primer año, 30 del último año y 10 graduados. Las calificaciones finales muestran que 3 estudiantes de primer año, 10 del último año y 5 de los graduados obtuvieron 10 en el curso. Si se elige un estudiante al azar de este grupo y se descubre que es uno de los que obtuvieron 10 de calificación, ¿cuál es la probabilidad de que sea un estudiante de último año?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 2.74.
5.2 Regla de multiplicación
Ejercicio 5.3
La probabilidad de que un hombre casado vea cierto programa de televisión es 0.4 y la probabilidad de que lo vea una mujer casada es 0.5. La probabilidad de que un hombre vea el programa, dado que su esposa lo ve, es 0.7. Calcule la probabilidad de que una pareja casada vea el programa.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 2.81.
Sean dos eventos A y B, entonces a partir de la definición de probabilidad condicional se tiene que,
P[A \cap B] = P[B] \, P[A|B] \quad \text{para} \quad P[B] > 0 \\ \text{ y } \\ P[A \cap B] = P[A] \, P[B|A] \quad \text{para} \quad P[A] > 0
Teniendo en cuenta lo anterior, ¿cuál es la solución del ejercicio Ejercicio 5.3?
Ejercicio 5.4 Tomando el experimento aleatorio que se ilustra en el siguiente enlace Coin-Dice Experiment, ¿si la probabilidad de “cara” (H) es igual a \frac{1}{4}, cuál es la probabilidad de que entre todos los resultados posibles del anterior experimento, se obtenga “sello” (T) en el lanzamiento de la moneda y seis (6) en el lanzamiento del dado?
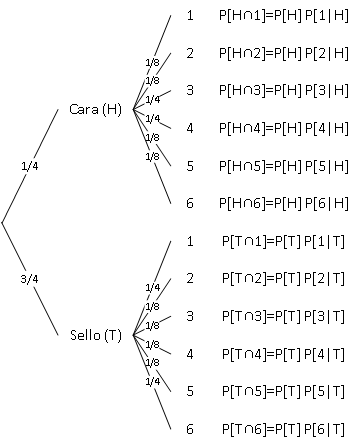
| P[Fila \cap Columna] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| H | \frac{1}{32} | \frac{1}{32} | \frac{2}{32} | \frac{2}{32} | \frac{1}{32} | \frac{1}{32} |
| T | \frac{6}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{6}{32} |
En general, sean una serie de eventos A_1, A_2, \dots, A_k tal que P[A_i] \neq 0 para todo i, entonces,
\begin{aligned} &P \left[ A_1 \cap A_2 \cap \dots \cap A_{k} \right] = \\ &\big( P[A_1] \big) \, \big( P[A_2|A_1] \big) \, \big( P[A_3|A_1 \cap A_2] \big) \, \dots \, \big( P \left[ A_k \left| A_1 \cap A_2 \cap \dots \cap A_{k-1} \right. \right] \big) \end{aligned}
5.3 Probabilidad total
Ejercicio 5.5
Una empresa industrial grande usa tres hoteles locales para ofrecer hospedaje nocturno a sus clientes. Se sabe por experiencia que a 20\% de los clientes se le asigna habitaciones en el Ramada Inn, a 50\% en el Sheraton y a 30\% en el Lakeview Motor Lodge. Si hay una falla en la plomería en 5\% de las habitaciones del Ramada Inn, en 4\% de las habitaciones del Sheraton y en 8\% de las habitaciones del Lakeview Motor Lodge, ¿cuál es la probabilidad de que a un cliente se le asigne una habitación en la que falle la plomería?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 2.109.
Teorema 5.1 (Probabilidad total) Si los eventos A_1, A_2, \dots, A_k con probabilidad diferente de cero, son una partición del espacio muestral (es decir, A_1 \cup A_2 \cup \cdots A_k = \Omega y A_i \cap A_j = \emptyset para todo i \neq j), entonces,
\begin{aligned} P[B] &= \sum_{i=1}^{k} P[A_i \cap B] \\ &= \sum_{i=1}^{k} P[A_i] \, P[B | A_i] \end{aligned}
Teniendo en cuenta lo anterior, ¿cuál es la solución del Ejercicio 5.5?
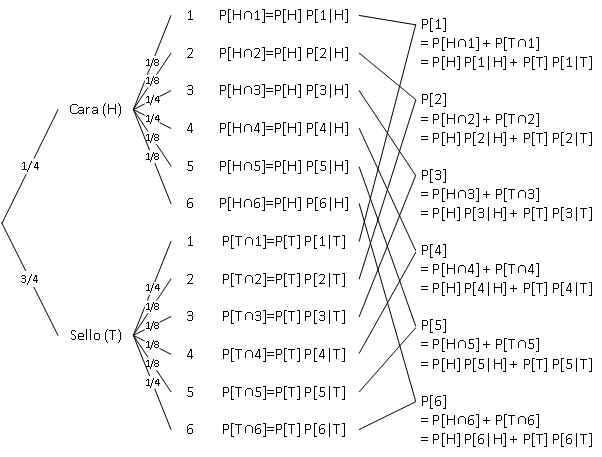
Ejercicio 5.6 Retomando el Ejercicio 5.4 (Coin-Dice Experiment con probabilidad de “cara” (H) igual a 1/4), ¿cuál es la probabilidad de que entre todos los resultados posibles del anterior experimento, se obtengan seis (6) en el dado?
De lo realizado en la sección anterior ya sabemos que,
| P[Fila \cap Columna] | 1 | 2 | 3 | 4 | 5 | 6 | P[Fila] |
|---|---|---|---|---|---|---|---|
| H | \frac{1}{32} | \frac{1}{32} | \frac{2}{32} | \frac{2}{32} | \frac{1}{32} | \frac{1}{32} | \frac{1}{4} |
| T | \frac{6}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{6}{32} | \frac{3}{4} |
y la respuesta a la pregunta realizada es uno de los valores de la siguiente tabla:
| \, | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P[Columna] | ¿? | ¿? | ¿? | ¿? | ¿? | ¿? |
| \, | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P[Columna] | \frac{7}{32} | \frac{4}{32} | \frac{5}{32} | \frac{5}{32} | \frac{4}{32} | \frac{7}{32} |
5.4 Regla de Bayes
Ejercicio 5.7
Se sabe que existe una probabilidad de 0.07 de que las mujeres de más de 60 años desarrollen cierta forma de cáncer. Se dispone de una prueba de sangre que, aunque no es infalible, permite detectar la enfermedad. De hecho, se sabe que 10\% de las veces la prueba da un falso negativo (es decir, la prueba da un resultado negativo de manera incorrecta) y 5\% de las veces la prueba da un falso positivo (es decir, la prueba da un resultado positivo de manera incorrecta). Si una mujer de más de 60 años se somete a la prueba y recibe un resultado favorable (es decir, negativo), ¿qué probabilidad hay de que realmente tenga la enfermedad?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 2.118.
Teorema 5.2 (Regla de Bayes) Si los eventos A_1, A_2, \dots, A_k con probabilidad diferente de cero, son una partición del espacio muestral (es decir, \bigcup_{i=1}^k A_i = \Omega y A_i \cap A_j = \emptyset para todo i \neq j), entonces,
\begin{aligned} P[A_j|B] &= \frac{P[A_j \cap B]}{P[B]} \\ &= \frac{P[A_j]P[B|A_j]}{P[B]} \\ &= \frac{P[A_j]P[B|A_j]}{\sum_{i=1}^{k} P[A_i] \, P[B | A_i]} \end{aligned}
Ejemplo 5.2 Ir a Bayes’ Theorem
Teniendo en cuenta lo anterior, ¿cuál es la solución del Ejercicio 5.7?
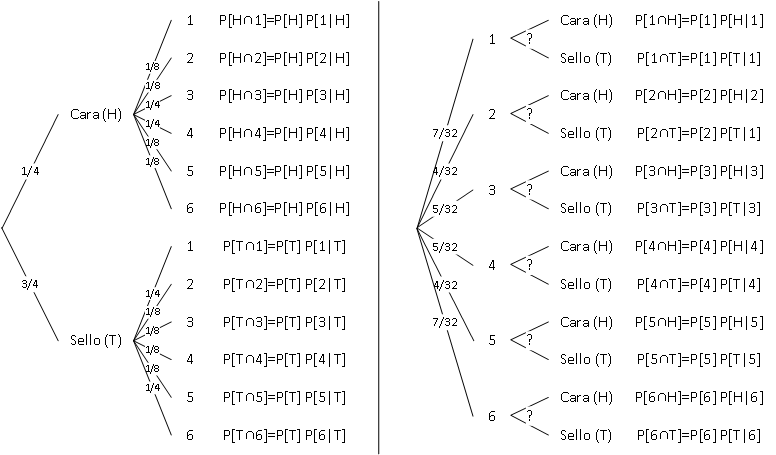
Ejercicio 5.8 Retomando el Ejercicio 5.4 (Coin-Dice Experiment, con probabilidad de “cara” (H) igual a 1/4), ¿cuál es la probabilidad de que entre todos los resultados posibles del anterior experimento, se haya obtenido “sello” (T) en la moneda, si ya se sabe que en el dado salió el número seis (6)?
Ya sabemos que,
| P[Columna|Fila] | 1 | 2 | 3 | 4 | 5 | 6 | Suma |
|---|---|---|---|---|---|---|---|
| H | \frac{1}{8} | \frac{1}{8} | \frac{1}{4} | \frac{1}{4} | \frac{1}{8} | \frac{1}{8} | 1 |
| T | \frac{1}{4} | \frac{1}{8} | \frac{1}{8} | \frac{1}{8} | \frac{1}{8} | \frac{1}{4} | 1 |
Queremos encontrar,
| P[Fila|Columna] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| H | ¿? | ¿? | ¿? | ¿? | ¿? | ¿? |
| T | ¿? | ¿? | ¿? | ¿? | ¿? | ¿? |
| Suma | 1 | 1 | 1 | 1 | 1 | 1 |
| P[Fila|Columna] | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| H | \frac{1}{7} | \frac{1}{4} | \frac{2}{5} | \frac{2}{5} | \frac{1}{4} | \frac{1}{7} |
| T | \frac{6}{7} | \frac{3}{4} | \frac{3}{5} | \frac{3}{5} | \frac{3}{4} | \frac{6}{7} |
| Suma | 1 | 1 | 1 | 1 | 1 | 1 |
5.5 Independencia
Ejercicio 5.9
Una estudiante universitaria frecuenta una de las dos cafeterías de su plantel, escogiendo Starbucks 70\% de las veces y Peet’s 30\% del tiempo. En cualquiera de estos lugares, ella compra un café de moka en 60\% de sus visitas.
- La siguiente vez que vaya a una cafetería en el plantel, ¿cuál es la probabilidad de que ella vaya a Starbucks y pida un café de moka?
- ¿Los dos eventos del inciso a. son independientes? Explique.
Mendenhall, Beaver & Beaver (2010). Introducción a la probabilidad y estadística. (13a. ed.) Cengage. Ejercicio 4.60.
Definición 5.2 (Independencia de dos eventos) Dos eventos A y B son independientes si y sólo si cualquiera de las siguientes tres igualdades se cumple (si una se cumple entonces se sabe que las otras dos también se van a cumplir):
- P[A|B] = P[A],
- P[B|A] = P[B],
- P\left[A \cap B\right] = P[A] \, P[B].
Teniendo en cuenta lo anterior, ¿cuál es la solución del Ejercicio 5.9?
Ejercicio 5.10 Retomando el Ejercicio 5.4 (Coin-Dice Experiment, con probabilidad de “cara” (H) igual a 1/4), el evento (a partir de de todos los resultados posibles del anterior experimento) en donde se obtiene “sello” (T) en el lanzamiento de la moneda es dependiente o independiente del evento (a partir de todos los resultados posibles del anterior experimento) en donde se obtienen seis (6) en el lanzamiento del dado?
Debido a que para este ejercicio en la secciones anteriores ya obtuvimos todas las probabilidades que podríamos llegar a necesitar, solamente debemos comparar adecuadamente los valores obtenidos, para poder determinar y probar dependencia o independencia de los eventos de la pregunta y de eventos similares.
Opción 1
Verificar que P[A|B] = P[A]:
| P[Fila|Columna] | 1 | 2 | 3 | 4 | 5 | 6 | P[Fila] |
|---|---|---|---|---|---|---|---|
| H | \frac{1}{7} | \frac{1}{4} | \frac{2}{5} | \frac{2}{5} | \frac{1}{4} | \frac{1}{7} | \frac{{1}}{4} |
| T | \frac{6}{7} | \frac{3}{4} | \frac{3}{5} | \frac{3}{5} | \frac{3}{4} | \frac{6}{7} | \frac{{3}}{4} |
| Suma | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Opción 2
Verificar que P[B|A] = P[B]:
| P[Columna|Fila] | 1 | 2 | 3 | 4 | 5 | 6 | Suma |
|---|---|---|---|---|---|---|---|
| H | \frac{1}{8} | \frac{1}{8} | \frac{1}{4} | \frac{1}{4} | \frac{1}{8} | \frac{1}{8} | 1 |
| T | \frac{1}{4} | \frac{1}{8} | \frac{1}{8} | \frac{1}{8} | \frac{1}{8} | \frac{1}{4} | 1 |
| P[Columna] | \frac{7}{32} | \frac{4}{32} | \frac{5}{32} | \frac{5}{32} | \frac{4}{32} | \frac{7}{32} | 1 |
Opción 3
Verificar que P\left[A \cap B\right] = P[A] \, P[B]:
| P[Fila \cap Columna] | 1 | 2 | 3 | 4 | 5 | 6 | P[Fila] |
|---|---|---|---|---|---|---|---|
| H | \frac{1}{32} | \frac{1}{32} | \frac{2}{32} | \frac{2}{32} | \frac{1}{32} | \frac{1}{32} | \frac{1}{4} |
| T | \frac{6}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{3}{32} | \frac{6}{32} | \frac{3}{4} |
| P[Columna] | \frac{7}{32} | \frac{4}{32} | \frac{5}{32} | \frac{5}{32} | \frac{4}{32} | \frac{7}{32} | 1 |
y
| \left(P[Fila]\right) \left(P[Columna]\right) | 1 | 2 | 3 | 4 | 5 | 6 | P[Fila] |
|---|---|---|---|---|---|---|---|
| H | \frac{7}{128} | \frac{4}{128} | \frac{5}{128} | \frac{5}{128} | \frac{4}{128} | \frac{7}{128} | \frac{1}{4} |
| T | \frac{21}{128} | \frac{12}{128} | \frac{15}{128} | \frac{15}{128} | \frac{12}{128} | \frac{21}{128} | \frac{3}{4} |
| P[Columna] | \frac{7}{32} | \frac{4}{32} | \frac{5}{32} | \frac{5}{32} | \frac{4}{32} | \frac{7}{32} | 1 |
Ejercicio 5.11 Suponga que un experimento aleatorio consiste en lanzar dos veces seguidas un dado de seis caras común y corriente. Teniendo en cuenta los eventos A = “Resultados en los cuales en el segundo lanzamiento se obtuvo un seis (6)” , B = “Resultados en los cuales al sumar lo obtenido en el primer y segundo lanzamiento nos da siete (7)” y C = “Resultados en los cuales al sumar lo obtenido en el primer y segundo lanzamiento nos da ocho (8)”:
- Verifique la dependencia o independencia de los eventos A y B.
- Verifique la dependencia o independencia de los eventos A y C.
Ejercicio 5.12
Una ciudad tiene dos carros de bomberos que operan de forma independiente. La probabilidad de que un carro específico esté disponible cuando se le necesite es 0.96.
- ¿Cuál es la probabilidad de que ninguno esté disponible cuando se necesite?
- ¿Cuál es la probabilidad de que un carro de bomberos esté disponible cuando se le necesite?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 2.89.
Definición 5.3 (Independencia de una serie de eventos) Una serie de eventos A_1, A_2, \dots, A_k son independientes si y sólo si,
\begin{aligned} P\left[\bigcap_{i \in I} A_i\right] &= \prod_{i \in I} P[A_i] \end{aligned} para todo I \subset \{1,2,\dots,k\} (lo que quiere decir que se deben verificar todas las intersecciones de dos eventos, las de tres eventos, las de cuatro, etc.).
- No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios de las secciones 2.6 y 2.7 del libro de Walpole o de las secciones 4.4 y 4.5 del libro de Anderson.