4 Conceptos básicos
En esta sección se hará una revisión de algunos temas relacionados con los conceptos básicos de probabilidad.
- Lea todo el contenido de la presente sección (Probabilidad, 4 Conceptos básicos), incluyendo el contenido de Apéndice, A Repaso: Conjuntos y Apéndice, B Repaso: Conteo.
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
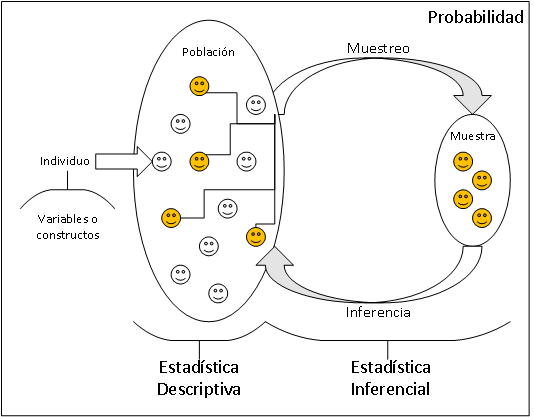
Recordemos la relación entre los tres grandes bloques del curso:
4.1 Experimento Aleatorio
Experimento aleatorio: Proceso que tiene más de un resultado posible y que cumple lo siguiente:
- Todos los posibles resultados son conocidos antes de realizar el experimento.
- En cualquier ejecución del experimento, el resultado no se puede conocer por anticipado.
- El experimento se debe poder repetir en condiciones “similares”.
Ejemplo 4.1 Lanzar un dado y observar el resultado. Enlace a la imagen: “The Wonderful World of dice”
Ejemplo 4.2 Sacar una carta de una mazo (baraja). Enlace a: “Standard 52-card deck - Wikipedia, Composition”
Ejemplo 4.3 Resultado de un partido.
Ejemplo 4.4 Precio de una acción mañana.
Ejemplo 4.5 Cantidad de unidades (de algún producto) vendidas el siguiente mes.
4.2 Espacio muestral
Espacio muestral: Conjunto de todos los resultados posibles de un experimento aleatorio (conjunto universal). Generalmente se denota con la letra omega mayúscula del alfabeto griego (\Omega).
Es evidente que es y será muy importante tener la mayor claridad posible acerca de los objetos matemáticos denominados conjuntos. Así mismo, se debe tener un buen manejo de su notación, sus relaciones, sus operaciones y sus propiedades. En el Apéndice A hay un pequeño y rápido repaso de este tema (Repaso: Conjuntos).
Ejercicio 4.1 A partir de los experimentos aleatorios del Ejemplo 4.1 al Ejemplo 4.5, identifique el espacio muestral correspondiente en cada caso.
El tipo de conjunto que es \Omega determina el tipo de espacio muestral: discreto o continuo.
4.3 Suceso o evento
Suceso o evento: Conjunto de algunos resultados posibles del experimento aleatorio (cualquier subconjunto del espacio muestral). Cualquier conjunto E tal que E \subset \Omega (cualquier conjunto dentro del conjunto universal).
Ejercicio 4.2 A partir de los experimentos aleatorios del Ejemplo 4.1 al Ejemplo 4.5, proponga una serie de sucesos/eventos para cada ejemplo.
4.4 Medida de probabilidad
4.4.1 Definición clásica
Definición clásica: Para un evento cualquiera (A \subset \Omega), la probabilidad de dicho evento (P[A]) es igual al número de resultados del evento sobre el total de resultados posibles del experimento aleatorio \left(P[A] = \frac{\#A}{\#\Omega}\right).
Esta manera de definir o asignar una probabilidad solamente es válida si:
El espacio muestral es finito ( \#\Omega < \infty ).
Todos los resultados del experimento aleatorio son igualmente probables \left( \forall \omega \in \Omega, P[\{w\}]=\frac{1}{\#\Omega} \right).
Es evidente que es y será muy importante establecer el número de elementos de un conjunto, lo cual no es trivial cuando no es práctico o no se puede listar todos los elementos. Por tal razón, es necesario establecer y usar mecanismos que permitan obtener esos “conteos” de elementos. En el Apéndice B hay un pequeño y rápido repaso de este tema (Repaso: Conteo).
Ejercicio 4.3 Calcule la probabilidad de los eventos propuestos en Ejercicio 4.3 asociados a los experimentos aleatorios del Ejemplo 4.1 y el Ejemplo 4.2.
4.4.2 Definición como frecuencia relativa
Definición como frecuencia relativa: Para un evento cualquiera (A \subset \Omega), la probabilidad de dicho evento (P[A]) es igual al número de repeticiones para las cuales el resultado pertenece al evento sobre el total de repeticiones del experimento aleatorio \left(P[A] = \frac{\text{Frecuencia absoluta de }A}{\text{Total repeticiones}}\right).
Entre más grande sea el número de repeticiones del experimento aleatorio, más cerca se estará del “verdadero valor” o el “valor exacto” de la probabilidad.
En los siguientes enlaces encontrarán una manera de poder simular las repeticiones de un cierto experimento aleatorio:
4.4.3 Definición subjetiva
Definición subjetiva: Para un evento cualquiera (A \subset \Omega), la probabilidad de dicho evento (P[A]) es asignada a partir de la intuición, de la experiencia, de las creencias, de la “experticia” en el tema o de otra fuente de información a nivel personal.
Ejercicio 4.4 ¿Cuál es la probabilidad de que no llueva en todo el día mañana en Bogotá, Colombia?
Ejercicio 4.5 ¿Cuál es la probabilidad de que la selección de fútbol de mayores colombiana gane su próximo partido oficial?
4.4.4 Axiomas
Los axiomas son unas premisas que se asumen, que no son una consecuencia de otras proposiciones, y que sirven de base para deducir y demostrar una serie de resultados dentro de una teoría.
Los siguientes axiomas se deben cumplir, para poder decir que P[\cdot] es una medida de probabilidad:
P[\Omega] = 1.
Para todo A \subset \Omega, P[A] \geq 0.
Para todo A_1, A_2, \dots \subset \Omega con A_i \cap A_j = \emptyset para i \neq j se tiene que P\big[ \bigcup_{i=1}^\infty A_i \big] = \sum_{i=1}^{\infty} P\left[ A_i \right]
Ejemplo 4.6 Ir a Simple Probability Experiment
4.4.5 Algunas propiedades
A partir de los axiomas se pueden demostrar los siguientes resultados.
Para todo A \subset \Omega y B \subset \Omega, se tiene que, si A \subset B entonces P[A] \leq P[B]
P[\emptyset] = 0
Para todo A \subset \Omega, 0 \leq P[A] \leq 1
Para todo A \subset \Omega y B \subset \Omega, P[A \cup B] = P[A] + P[B] - P[A \cap B]
Para todo A \subset \Omega, P\left[A^C\right] = 1 - P[A]
Note que:
\begin{aligned} P : \wp (\Omega) &\longrightarrow [0,1] \\ A &\longrightarrow P[A] \end{aligned}
4.5 Ejercicios
A continuación se encuentran una serie de ejercicios tomados del siguiente libro:
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación.
Ejercicio 4.6 (Walpole 2.49)
Encuentre los errores en cada una de las siguientes aseveraciones:
Las probabilidades de que un vendedor de automóviles venda 0, 1, 2 o 3 unidades en un día dado de febrero son 0.19, 0.38, 0.29 y 0.15, respectivamente.
La probabilidad de que llueva mañana es 0.40 y la probabilidad de que no llueva es 0.52.
Las probabilidades de que una impresora cometa 0, 1, 2, 3 o 4 o más errores al imprimir un documento son 0.19, 0.34, -0.25, 0.43 y 0.29, respectivamente.
Al sacar una carta de una baraja en un solo intento la probabilidad de seleccionar un corazón es 1/4, la probabilidad de seleccionar una carta negra es 1/2, y la probabilidad de seleccionar una carta de corazones y negra es 1/8.
Ejercicio 4.7 (Walpole 2.61)
En un grupo de 100 estudiantes graduados de preparatoria, 54 estudiaron matemáticas, 69 estudiaron historia y 35 cursaron matemáticas e historia. Si se selecciona al azar uno de estos estudiantes, calcule la probabilidad de que
el estudiante haya cursado matemáticas o historia;
el estudiante no haya llevado ninguna de estas materias;
el estudiante haya cursado historia pero no matemáticas
Ejercicio 4.8 (Walpole 2.55)
Si cada artículo codificado en un catálogo empieza con 3 letras distintas seguidas por 4 dígitos distintos de cero, calcule la probabilidad de seleccionar aleatoriamente uno de estos artículos codificados que tenga como primera letra una vocal y el último dígito sea par.
Ejercicio 4.9 (Walpole 2.58)
Se lanza un par de dados. Calcule la probabilidad de obtener
un total de 8;
máximo un total de 5.
Ejercicio 4.10 (Walpole 2.59)
En una mano de póquer que consta de 5 cartas, encuentre la probabilidad de tener
3 ases;
4 cartas de corazones y 1 de tréboles.
Ejercicio 4.11 (Walpole 2.60)
Si se toman 3 libros al azar, de un librero que contiene 5 novelas, 3 libros de poemas y 1 diccionario, ¿cuál es la probabilidad de que
se seleccione el diccionario?
se seleccionen 2 novelas y 1 libro de poemas?
- No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios de las secciones 2.1 a 2.5 del libro de Walpole o de las secciones 4.1 a 4.3 del libro de Anderson.
De manera opcional, quien quiera puede buscar, consultar, leer, y aprender por su cuenta, acerca de:
- Las deducciones analíticas (demostraciones) de las propiedades de una medida de probabilidad.
- Otros resultados o fórmulas de conteo, adicionales a las incluidas en el Apéndice B.