12 Estimación por intervalo
En esta sección se hará una revisión de algunos aspectos relacionados con la estimación por intervalo (intervalos de confianza) de un parámetro de interés.
12.1 Para empezar
- Lea todo el contenido de la presente sección (Inferencia, 12. Estimación por intervalo).
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
12.2 Aspectos generales
Tengamos en cuenta la siguiente situación:
The Wall Street Journal informó que en 2008 los accidentes automovilísticos le costaron \$162 mil millones a Estados Unidos (The Wall Street Journal, 5 de marzo de 2008). El costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida, fue considerado de \$1599. Suponga que este costo promedio se basó en una muestra de 50 personas que estuvieron involucradas en dichos percances y que la desviación estándar poblacional es \$600. Proporcione una estimación mediante un intervalo de confianza de 90\% para el costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 6.
Sea P\left[ \hat{\theta}_L < \theta < \hat{\theta}_U \right] = 1 - \alpha para 0 < \alpha < 1.
El intervalo \left(\hat{\theta}_L, \hat{\theta}_U \right) es llamado intervalo de confianza del 100(1-\alpha)\%.
1-\alpha es el grado de confianza.
\hat{\theta}_L es el límite de confianza inferior.
\hat{\theta}_U es el límite de confianza superior.
La distribución de un estadístico que relaciona el parámetro de interés (\theta) con su estimador puntual (T) me sirve para obtener una estimación por intervalo (intervalo de confianza) para el parámetro.
12.3 Una población
12.3.1 Media
Según la distribución muestral de la media, cuando \sigma es conocida, g(T, \theta) = g(\bar{X}, \mu) = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \sim \mathcal{N}(0,1) entonces, \begin{aligned} P \left[ a < g(T, \theta) < b \right] &= 1 - \alpha \\ P \left[ a < g(\bar{X}, \mu) < b \right] &= 1 - \alpha \\ P \left[ - z_{(\alpha/2)} < Z < z_{(\alpha/2)} \right] &= 1 - \alpha \\ P \left[ - z_{(\alpha/2)} < \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} < z_{(\alpha/2)} \right] &= 1 - \alpha \\ P \left[ - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} < \bar{X} - \mu < z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \\ P \left[ - \bar{X} - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} < - \mu < - \bar{X} + z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \\ P \left[ \bar{X} - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} < \mu < \bar{X} + z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \end{aligned} A partir de lo cual, concluimos que, bajo el supuesto de que se cumplen todas las condiciones que permiten usar la distribución muestral que se usó, y dónde, \begin{aligned} \hat{\theta}_L &= \underbrace{ \underbrace{ \bar{x} }_{\substack{\text{estimación} \\ \text{puntual}}} - \underbrace{ \underbrace{ z_{(\alpha/2)} }_\text{cuantil} \underbrace{ \frac{\sigma}{\sqrt{n}} }_{\substack{\text{error} \\ \text{estándar}}} }_\text{margen de error} }_\text{límite inferior} \\ \hat{\theta}_U &= \underbrace{ \underbrace{ \bar{x} }_{\substack{\text{estimación} \\ \text{puntual}}} + \underbrace{ \underbrace{ z_{(\alpha/2)} }_\text{cuantil} \underbrace{ \frac{\sigma}{\sqrt{n}} }_{\substack{\text{error} \\ \text{estándar}}} }_\text{margen de error} }_\text{límite superior} \end{aligned} entonces \left(\hat{\theta}_L, \hat{\theta}_U \right) es un intervalo de confianza del 100(1-\alpha)\% para la media poblacional (\theta = \mu) de la variable de interés.
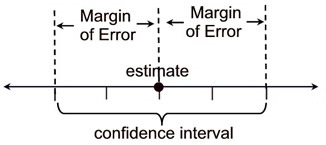
Para ilustrar: Explore Coverage of Confidence Intervals
Fácilmente se puede deducir que, bajo los respectivos supuestos, los intervalos de confianza bilateral y unilaterales para la media \mu son:
Si \sigma es conocida, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de la población tiene distribución normal tenemos que,
Bilateral: \left( \bar{x} - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \; , \; \bar{x} + z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right)
Unilateral a la derecha: \left( - \infty \; , \; \bar{x} + z_{(\alpha)} \frac{\sigma}{\sqrt{n}} \right)
Unilateral a la izquierda: \left( \bar{x} - z_{(\alpha)} \frac{\sigma}{\sqrt{n}} \; , \; \infty \right)
Si \sigma es desconocida, entonces, bajo el supuesto de que la variable de interés de la población tiene distribución normal tenemos que,
Bilateral: \left( \bar{x} - t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}} \; , \; \bar{x} + t_{(\alpha/2,n-1)} \frac{s}{\sqrt{n}} \right),
Unilateral a la derecha: \left( - \infty \; , \; \bar{x} + t_{(\alpha,n-1)} \frac{s}{\sqrt{n}} \right)
Unilateral a la izquierda: \left( \bar{x} - t_{(\alpha,n-1)} \frac{s}{\sqrt{n}} \; , \; \infty \right)
Para ilustrar:
Ejercicio 12.1
The Wall Street Journal informó que en 2008 los accidentes automovilísticos le costaron \$162 mil millones a Estados Unidos (The Wall Street Journal, 5 de marzo de 2008). El costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida, fue considerado de \$1599. Suponga que este costo promedio se basó en una muestra de 50 personas que estuvieron involucradas en dichos percances y que la desviación estándar poblacional es \$600.
- Proporcione una estimación mediante un intervalo de confianza de 90\% para el costo promedio por persona de los accidentes automovilísticos en el área de Tampa, Florida.
- ¿Cuál es el margen de error para un intervalo de 90\% de confianza?
- ¿Qué recomendaría si el estudio requiriera un margen de error de \$150 o menos?
- ¿Qué le sucede a la amplitud del intervalo de confianza a medida que el nivel de confianza aumenta (90\%, 95\%, 99%)? ¿Qué le sucede a la amplitud del intervalo de confianza a medida que el tamaño de muestra aumenta (50, 100, 500)?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 6.
Ejercicio 12.2
Una máquina produce piezas metálicas de forma cilíndrica. Se toma una muestra de las piezas y los diámetros son 1.01, 0.97, 1.03, 1.04, 0.99, 0.98, 0.99, 1.01 y 1.03 centímetros.
- ¿Cuál es la estimación puntual de la media poblacional?
- ¿Cuál es la estimación puntual de la desviación estándar poblacional?
- Con 95\% de confianza, ¿cuál es el margen de error para la estimación de la media poblacional?
- ¿Cuál es el intervalo de confianza de 95\% para la media poblacional?
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 9.11.
12.3.1.1 Tamaño de muestra
¿Qué tan grande debería ser el tamaño de muestra para que el margen de error del intervalo de confianza deseado sea como máximo un valor fijo dado? En otras palabras, ¿qué tan grande debería ser el tamaño de la muestra n para que, con un 100(1-\alpha)\% de confianza, \left| T - \theta \right| sea a lo más un valor fijo dado e?
Para T = \bar{X} y \theta = \mu, utilizando la distribución muestral de la media cuando \sigma es conocida, se tiene que:
\begin{aligned} P \left[ \bar{X} - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} < \mu < \bar{X} + z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \\ P \left[ - z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} < \mu - \bar{X} < z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \\ P \left[ \left| \mu - \bar{X} \right| < z_{(\alpha/2)} \frac{\sigma}{\sqrt{n}} \right] &= 1 - \alpha \\ \end{aligned}
entonces, e = \frac{z_{(\alpha/2)} \, \sigma}{\sqrt{n}}, y despejando, n = \left(\frac{z_{(\alpha/2)} \, \sigma}{e} \right)^2.
Es decir, si \bar{x} es usada para estimar \mu y \sigma es conocida, se tiene un 100(1-\alpha)\% de confianza de que el error no va a exceder un valor fijo dado e, cuando el tamaño de muestra es:
\begin{aligned} n &= \left( \frac{z_{(\alpha/2)} \, \sigma}{e} \right)^2 \\ &= \frac{z^2_{(\alpha/2)} \, \sigma^2}{e^2} \end{aligned}
El tamaño de muestra anterior asume \sigma conocida, pero si esta no es conocida:
- Use la desviación estándar estimada calculada a partir de un estudio previo.
- Haga un estudio piloto con una muestra preliminar y use la desviación estándar estimada calculada a partir de esa muestra preliminar.
- Use un valor dado por un “experto” o la cuarta parte del que creemos será el rango de la variable: \frac{\text{Posible máximo}-\text{Posible mínimo}}{4}.
Ejercicio 12.3
Se efectúan pruebas de rendimiento de gasolina con un determinado modelo de automóvil. Si se desea dar un intervalo de confianza de 98\% con un margen de error de 1 milla por galón, ¿cuántos automóviles deberán usarse? Suponga que por pruebas anteriores se sabe que la desviación estándar del rendimiento es 2.6 millas por galón.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 50.
12.3.2 Proporción
Fácilmente se puede deducir que, para n suficientemente grande (np > 10 y n(1-p) > 10), los intervalos de confianza bilateral y unilaterales de la proporción p son:
Bilateral: \left( \hat{p} - z_{(\alpha/2)} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \; , \; \hat{p} + z_{(\alpha/2)} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right)
Unilateral a la derecha: \left( - \infty \; , \; \hat{p} + z_{(\alpha)} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right)
Unilateral a la izquierda: \left( \hat{p} - z_{(\alpha)} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \; , \; \infty \right)
Para ilustrar:
Ejercicio 12.4
En un estudio de USA Today/CNN/Gallup realizado con 369 padres que trabajan, se encontró que 200 consideran que pasan muy poco tiempo con sus hijos debido a sus compromisos laborales.
- Proporcione una estimación puntual de la proporción poblacional de padres que trabajan y piensan que pasan muy poco tiempo con sus hijos debido a sus compromisos laborales.
- ¿Cuál es el error estándar de la estimación puntual anterior?
- ¿Cuál es el margen de error para 95\% de confianza?
- ¿Cuál es el intervalo de confianza de 95\% para la proporción poblacional de padres que trabajan y piensan que pasan muy poco tiempo con sus hijos debido a sus compromisos ocupacionales?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 54.
12.3.2.1 Tamaño de muestra
Si \hat{p} es usada para estimar p, se tiene un 100(1-\alpha)\% de confianza de que el error no va a exceder un valor fijo dado e, cuando el tamaño de muestra es:
n \geq \left( \frac{z_{(\alpha/2)} \, \sqrt{p^*(1-p^*)}}{e} \right)^2 = \frac{z^2_{(\alpha/2)} \, p^*(1-p^*)}{e^2}
con p^* ojalá lo más cercano posible al desconocido valor de p.
Por otra parte, no puedo usar p^* = \hat{p}, porque ni siquiera he determinado cuál va a ser el tamaño de la muestra n (aún no tengo datos muestrales para calcular \hat{p}). Entonces, para p^* tenemos las siguientes opciones:
- Use una proporción estimada obtenida a partir de un estudio previo.
- Use una proporción estimada obtenida a partir de una muestra preliminar.
- Use un valor dado por un “experto”.
- Use p^* = 0.5. Este es el “peor” escenario posible, ya que es el p^* que maximiza n.
Ejercicio 12.5
Una firma de tarjetas de crédito de un conocido banco desea estimar la proporción de tarjetahabientes que al final del mes tienen un saldo distinto de cero que ocasiona cargos. Suponga que el margen de error deseado es 0.03 con 98\% de confianza.
- ¿De qué tamaño deberá tomarse la muestra si se cree que 70\% de los tarjetahabientes de la firma tienen un saldo distinto de cero al final del mes?
- ¿De qué tamaño deberá tomarse la muestra si no se puede especificar ningún valor planeado para la proporción?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 58.
12.3.3 Varianza
Fácilmente se puede deducir que, bajo el supuesto de que la variable de interés de la población tiene distribución normal, los intervalos de confianza bilateral y unilaterales para la varianza \sigma^2 son:
Bilateral: \left( \frac{(n-1) s^2}{\chi^2_{(\alpha/2,n-1)}} \; , \; \frac{(n-1) s^2}{\chi^2_{(1-\alpha/2,n-1)}} \right)
Unilateral a la derecha: \left( - \infty \; , \; \frac{(n-1) s^2}{\chi^2_{(1-\alpha/2,n-1)}} \right)
Unilateral a la izquierda: \left( \frac{(n-1) s^2}{\chi^2_{(\alpha/2,n-1)}} \; , \; \infty \right)
Para ilustrar:
¿Qué debería hacer para, a partir de lo anterior, obtener los intervalos de confianza bilateral y unilaterales para la desviación estándar \sigma?
Ejercicio 12.6
Un fabricante de baterías para automóvil afirma que sus baterías durarán, en promedio, 3 años con una varianza de 1 año. Suponga que 5 de estas baterías tienen duraciones de 1.9, 2.4, 3.0, 3.5 y 4.2 años y con base en esto construya un intervalo de confianza del 95\% para la desviación estándar poblacional, después decida si es válida la afirmación del fabricante de que dicha desviación estándar poblacional es igual a 1. Suponga que la población de duraciones de las baterías se distribuye de forma aproximadamente normal.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 9.71.
12.4 Dos poblaciones
12.4.1 Medias
Fácilmente se puede deducir que, bajo ciertos supuestos, el intervalo de confianza bilateral (los unilaterales también son fáciles de deducir) para la diferencia de medias \mu_1 - \mu_2 es:
Si son observaciones pareadas, entonces haga:
X = X_1 - X_2 lo que implica que \bar{X} = \bar{X}_1 - \bar{X}_2 y \mu = \mu_1 - \mu_2, quedando así en la situación de la media de una población (para los anteriores X, \bar{X} y \mu).
Si NO son observaciones pareadas, con \sigma_1 y \sigma_2 conocidas, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,
\begin{aligned} &\left( \left( \bar{x}_1 - \bar{x}_2 \right) - z_{(\alpha/2)} \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}} \right. , \\ &\quad \left. \left( \bar{x}_1 - \bar{x}_2 \right) + z_{(\alpha/2)} \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}} \right) \end{aligned}
Si NO son observaciones pareadas y se considera que \sigma_1 = \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,
\begin{aligned} &\left( \left( \bar{x}_1 - \bar{x}_2 \right) - t_{(\alpha/2,n_1+n_2-2)} \, s_p \, \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \right. , \\ &\quad \left. \left( \bar{x}_1 - \bar{x}_2 \right) + t_{(\alpha/2,n_1+n_2-2)} \, s_p \, \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \right) \end{aligned} donde, s_p = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}
Si NO son observaciones pareadas y se considera que \sigma_1 \neq \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal se tiene que,
\begin{aligned} &\left( \left( \bar{x}_1 - \bar{x}_2 \right) - t_{(\alpha/2,\nu)} \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} \right. , \\ &\quad \left. \left( \bar{x}_1 - \bar{x}_2 \right) + t_{(\alpha/2,\nu)} \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} \right) \end{aligned} donde, \nu = \left\lfloor \frac{\left(s_1^2/n_1+s_2^2/n_2\right)^2}{\frac{\left(s_1^2/n_1\right)^2}{n_1-1} + \frac{\left(s_2^2/n_2\right)^2}{n_2-1}} \right\rfloor
Ejercicio 12.7
Un fabricante produce dos modelos de una lijadora automática, uno de lujo y otro estándar, diseñado para uso doméstico. Los precios de venta de una muestra de distribuidores minoristas se presentan a continuación.
Minorista 1 2 3 4 5 6 7 Lujo 39 39 45 38 40 39 35 Estánda r 27 28 35 30 30 34 29 ¿Cuál es el intervalo de 95\% de confianza para la diferencia entre la media de los precios de ambos modelos?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 10. Ejercicio 27.
Ejercicio 12.8
Se esperaba que el Día de San Valentín el gasto promedio fuera de \$100.89 (USA Today, 13 de febrero de 2006). ¿Hay diferencia en las cantidades que desembolsan los hombres y las mujeres? El gasto promedio en una muestra de 40 hombres fue de \$135.67 y en una muestra de 30 mujeres fue de \$68.64. Por estudios anteriores se sabe que la desviación estándar poblacional en el consumo de los hombres es \$35 y en el de las mujeres es \$20.
- ¿Cuál es la estimación puntual de la diferencia entre el gasto medio poblacional de los hombres y el gasto medio poblacional de las mujeres?
- Con 99\% de confianza, ¿cuál es el margen de error?
- Elabore un intervalo de confianza de 99\% para la diferencia entre las dos medias poblacionales.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 10. Ejercicio 5.
Ejercicio 12.9
Los siguientes datos representan el tiempo de duración de películas producidas por dos empresas cinematográficas.
Empresa I 103 94 110 87 98 II 97 82 123 92 175 88 118 Calcule un intervalo de confianza del 90\% para la diferencia entre la duración promedio de las películas que producen las dos empresas. Suponga que las diferencias en la duración se distribuyen de forma aproximadamente normal y que tienen varianzas iguales.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 9.46.
Ejercicio 12.10
Los siguientes datos representan el tiempo de duración de películas producidas por dos empresas cinematográficas.
Empresa I 103 94 110 87 98 II 97 82 123 92 175 88 118 Calcule un intervalo de confianza del 90\% para la diferencia entre la duración promedio de las películas que producen las dos empresas. Suponga que las diferencias en la duración se distribuyen de forma aproximadamente normal y que tienen varianzas distintas.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 9.46.
12.4.2 Proporciones
Fácilmente se puede deducir que, bajo ciertos supuestos, el intervalo de confianza bilateral para la diferencia de proporciones p_1 - p_2 es:
Si son observaciones pareadas, entonces haga
X = X_1 - X_2 lo que implica que \bar{X} = \hat{P}_1 - \hat{P}_2 y \mu = p_1 - p_2, quedando así en la situación de la media de una población (para los anteriores X, \bar{X} y \mu).
Si NO son observaciones pareadas y se considera que p_1 = p_2, entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right) se tiene que,
\begin{aligned} &\left( \left( \hat{p}_1 - \hat{p}_2 \right) - z_{(\alpha/2)} \sqrt{\hat{p} (1-\hat{p}) \left(\frac{1}{n_1}+\frac{1}{n_2}\right)} \right. , \\ &\quad \left. \left( \hat{p}_1 - \hat{p}_2 \right) + z_{(\alpha/2)} \sqrt{\hat{p} (1-\hat{p}) \left(\frac{1}{n_1}+\frac{1}{n_2}\right)} \right) \end{aligned} donde, \hat{p} = \frac{n_1 \hat{p}_1 + n_2 \hat{p}_2}{n_1 + n_2}
Si NO son observaciones pareadas y se considera que p_1 \neq p_2, entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right) se tiene que,
\begin{aligned} &\left( \left( \hat{p}_1 - \hat{p}_2 \right) - z_{(\alpha/2)} \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \right. , \\ &\quad \left. \left( \hat{p}_1 - \hat{p}_2 \right) + z_{(\alpha/2)} \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \right) \end{aligned}
Ejercicio 12.11
En una encuesta de BusinessWeek/Harris se pidió a los ejecutivos de empresas grandes su opinión acerca de cómo veían las perspectivas económicas para el futuro. Una de las preguntas era: ¿Piensa usted que en los próximos 12 meses aumentará en su empresa el número de empleados de tiempo completo? En la encuesta actual, 220 de 400 ejecutivos respondieron Sí, mientras que en la realizada el año anterior, 192 de 400 respondieron en el mismo sentido.
- Calcule la proporción muestral de los que respondieron Sí en la encuesta actual y la proporción de los que respondieron Sí en la encuesta anterior.
- ¿Cuál es la estimación puntual de la diferencia entre las proporciones de las dos poblaciones? ¿Qué indica tal estimación? ¿Cuál es el error estándar de dicha estimación puntual?
- Encuentre un intervalo de 95\% de confianza para estimar la diferencia entre las proporciones en estas dos encuestas. ¿Cuál es su interpretación de la estimación por intervalo?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 10. Ejercicio 30.
12.4.3 Varianzas
Fácilmente se puede deducir que, bajo el supuesto de que la variable de interés de la población tiene distribución normal, el intervalo de confianza bilateral para el cociente de varianzas \sigma_1^2/\sigma_2^2 es:
\begin{aligned} &\left( \frac{s_1^2}{s_2^2} \frac{1}{f_{(\alpha/2,n_1-1,n_2-1)}} \; , \; \frac{s_1^2}{s_2^2} \frac{1}{f_{(1-\alpha/2,n_1-1,n_2-1)}} \right) \\ &= \left( \frac{s_1^2}{s_2^2} \frac{1}{f_{(\alpha/2,n_1-1,n_2-1)}} \; , \; \frac{s_1^2}{s_2^2} f_{(\alpha/2,n_2-1,n_1-1)} \right) \end{aligned}
¿Qué debería hacer para, a partir de lo anterior, obtener un intervalo de confianza bilateral para el cociente de desviaciones estándar \sigma_1/\sigma_2?
Ejercicio 12.12
Ejercicio 9.79. Construya un intervalo de confianza del 90\% para \sigma_1 / \sigma_2 en el ejercicio 9.46 de la página 295. ¿Deberíamos suponer que las varianzas poblacionales son iguales cuando construimos nuestro intervalo de confianza para la diferencia de los promedios poblacionales?
Ejercicio 9.46. Los siguientes datos representan el tiempo de duración de películas producidas por dos empresas cinematográficas.
Empresa I 103 94 110 87 98 II 97 82 123 92 175 88 118 Calcule un intervalo de confianza del 90\% para la diferencia entre la duración promedio de las películas que producen las dos empresas. Suponga que las diferencias en la duración se distribuyen de forma aproximadamente normal.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 9.46 y 9.79.
12.5 Al finalizar
- No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios del capítulo 9 (sin las secciones 9.6, 9.7 y 9.14) del libro de Walpole o de los capítulos 8, 10 y 11 (solamente los ejercicios de estimación por intervalo) del libro de Anderson.