10 Estimación puntual
En esta sección se hará una revisión de algunos aspectos relacionados con la estimación puntual de parámetros.
- Lea todo el contenido de la presente sección (Inferencia, 10 Estimación puntual).
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
10.1 Definiciones
La idea detrás de la estimación puntual de parámetros es obtener, a partir de los valores de la muestra, una “buena aproximación” para el valor de un parámetro de interés (sin datos poblacionales no puedo saber el verdadero valor de un parámetro).
Definición 10.1 (Estimador puntual) Un estimador puntual de un parámetro \theta es una función de una muestra aleatoria \big( T(X_1, \dots, X_n) \big) que tiene como objetivo la estimación de ese parámetro.
Definición 10.2 (Estimación puntual) Una estimación puntual de un parámetro \theta es el valor que resulta al usar el estimador puntual sobre un conjunto de valores que toma la muestra aleatoria (es decir, sobre los datos de mi muestra).
Ejercicio 10.1 Teniendo en cuenta los diez resultados que obtuvo al lanzar una moneda 10 veces consecutivas (es decir, la realización de la muestra aleatoria de tamaño 10 que usted obtuvo).
- ¿Qué estimador, es decir, qué función de la muestra \big(T(X_1,...,X_n)\big) utilizaría para estimar el o los parámetros (identificados en el Ejercicio 9.3)?
- ¿Cuál sería la estimación respectiva?
- Suponga que todos los estudiantes hacen el ejercicio con la misma moneda, ¿todos obtienen la misma estimación? ¿por qué?
Existen varios métodos para encontrar estimadores, como el método de momentos (solución de sistema de ecuaciones), el de máxima verosimilitud o el de mínimos cuadrados (problemas de optimización), entre otros. Sin embargo, ese tema no hace parte del alcance y temario de este material.
Para más información acerca de este tema, pueden consultar la sección Obtención de estimadores de mi material del curso Inferencia Estadística de la malla curricular de la Carrera de Estadística.
Sea X_1, \dots, X_n una muestra aleatoria y sean x_1, \dots, x_n los valores que tomó dicha muestra. Entonces,
Un estimador puntual para \theta = \mu puede ser \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i con estimación puntual \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
Un estimador puntual para \theta = p (Bernoulli) puede ser \bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i = \frac{\#\,1\text{'s}}{n} = \hat{P} con estimación puntual \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i = \frac{\#\,1\text{'s}}{n} = \hat{p}
Un estimador puntual para \theta = \sigma^2 puede ser M^2 = \frac{1}{n} \sum_{i=1}^{n} \left(X_i - \bar{X}\right)^2 con estimación puntual m^2 = \frac{1}{n} \sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2
Un estimador puntual para \theta = \sigma^2 puede ser S^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left(X_i - \bar{X}\right)^2 con estimación puntual s^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2
Si tengo varios estimadores para un mismo parámetro, ¿cuál utilizo?, ¿cuál es mejor?, ¿es mejor utilizar M^2 o S^2?.
El contenido de la siguiente subsección es el que nos permitirá dar una respuesta a la anterior pregunta.
10.2 Evaluar un estimador
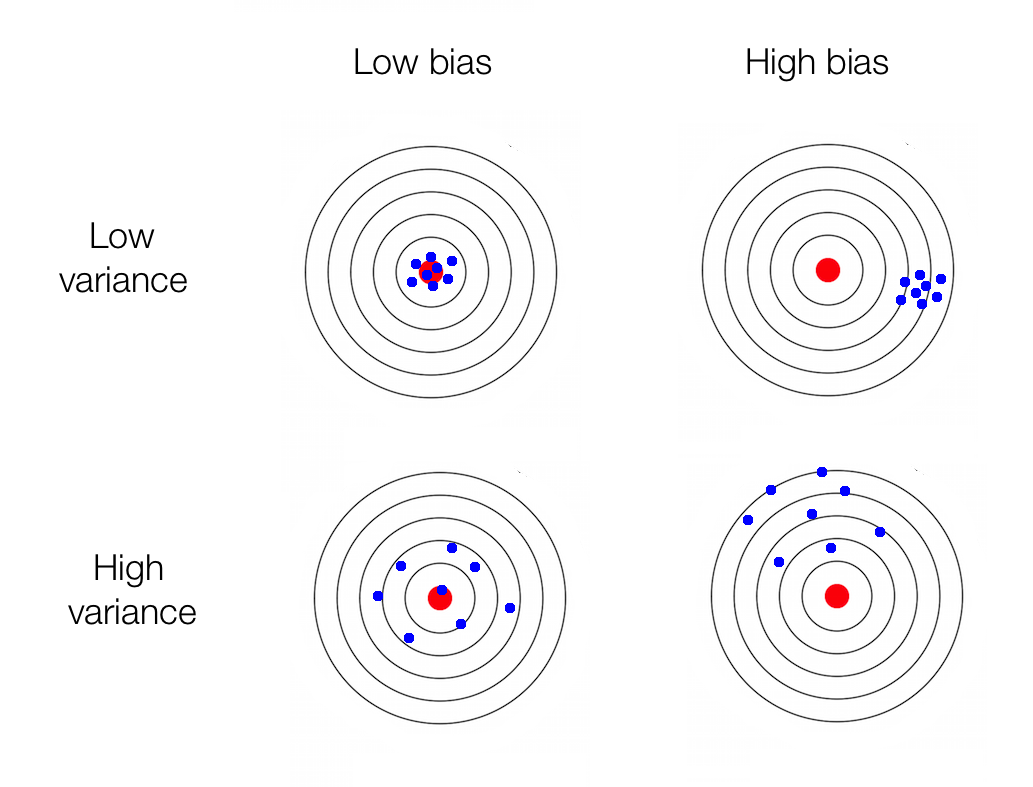
Queremos estimadores lo menos sesgados que se pueda y que a la vez tengan la menor varianza posible.
10.2.1 Algunas propiedades de \bar{X}
Sea X_1, X_2, \dots, X_n una muestra aleatoria de tamaño n de la población con distribución F_X, cuya media es \mu y cuya varianza es \sigma^2; para T(X_1, \dots, X_n) = \frac{1}{n} (X_1 + \dots + X_n) = \frac{1}{n} \sum_{i=1}^{n} X_i = \bar{X} se tiene que,
E\left[ \bar{X} \right] = \mu
\begin{aligned} E\left[\bar{X}\right] &= E\left[\frac{1}{n} \sum_{i=1}^{n} X_i\right] \\ &= \frac{1}{n} \sum_{i=1}^{n} E\left[X_i\right]\\ &= \frac{1}{n} \sum_{i=1}^{n} \mu \\ &= \frac{1}{n} \, n \, \mu \\ &= \mu \end{aligned}
Var\left[\bar{X}\right] = \frac{\sigma^2}{n}
\begin{aligned} Var\left[\bar{X}\right] &= Var\left[\frac{1}{n} \sum_{i=1}^{n} X_i\right] \\ &= \frac{1}{n^2} Var\left[\sum_{i=1}^{n} X_i\right] \\ &= \frac{1}{n^2} \sum_{i=1}^{n} Var\left[ X_i \right] \\ &= \frac{1}{n^2} \sum_{i=1}^{n} \sigma^2 \\ &= \frac{1}{n^2} \, n \, \sigma^2 \\ &= \frac{\sigma^2}{n} \end{aligned}
E\left[ \bar{X}^2 \right] = \frac{\sigma^2}{n} + \mu^2
\begin{aligned} Var\left[\bar{X}\right] &= \frac{\sigma^2}{n}\\ E\left[ \bar{X}^2 \right] - E\left[ \bar{X} \right]^2 &= \frac{\sigma^2}{n}\\ E\left[ \bar{X}^2 \right] - \mu^2 &= \frac{\sigma^2}{n}\\ E\left[ \bar{X}^2 \right] &= \frac{\sigma^2}{n} + \mu^2 \end{aligned}
10.2.2 Sesgo (bias)
Definición 10.3 (Sesgo) El sesgo de un estimador T con respecto a un parámetro \theta se define como SESGO(T) = E[T] - \theta.
Definición 10.4 (Insesgado) T es un estimador insesgado de un parámetro \theta, si SESGO(T) = 0, o lo que es lo mismo, si E[T] = \theta.
Ejemplo 10.1 Sesgo del estimador T = \bar{X} para estimar el parámetro \theta = \mu:
\begin{aligned} SESGO(T) &= E[T] - \theta \\ SESGO\left(\bar{X}\right)&= E\left[\bar{X}\right] - \mu \\ &= \mu - \mu \\ &= 0 \end{aligned}
Ejemplo 10.2 Sesgo del estimador T = M^2 para estimar el parámetro \theta = \sigma^2:
SESGO\left(M^2\right) = - \frac{\sigma^2}{n}
\begin{aligned} SESGO(T) &= E[T] - \theta \\ SESGO\left(M^2\right) &= E\left[M^2\right] - \sigma^2 \\ &= E\left[\frac{1}{n} \sum_{i=1}^{n} \left(X_i - \bar{X}\right)^2\right] - \sigma^2 \\ &= E\left[ \frac{1}{n} \sum_{i=1}^{n} X_i^2 - \bar{X}^2 \right] - \sigma^2 \\ &= \frac{1}{n} \sum_{i=1}^{n} E\left[X_i^2\right] - E\left[ \bar{X}^2 \right] - \sigma^2 \\ &= \frac{1}{n} \, n \, \left(\sigma^2 + \mu^2\right) - \left(\frac{\sigma^2}{n} + \mu^2\right) - \sigma^2 \\ &= \sigma^2 + \mu^2 - \frac{\sigma^2}{n} - \mu^2 - \sigma^2 \\ &= - \frac{\sigma^2}{n} \end{aligned}
El estimador T = M^2 subestimará al parámetro \theta = \sigma^2, ya que SESGO\left(M^2\right) = - \frac{\sigma^2}{n} < 0. Sin embargo, por lo menos se tiene que, a medida que el tamaño de muestra aumenta el sesgo se aproxima a cero, SESGO\left(M^2\right) = - \frac{\sigma^2}{n} \underset{n \to \infty}{\longrightarrow} 0.
Ejemplo 10.3 Sesgo del estimador T = S^2 para estimar el parámetro \theta = \sigma^2:
SESGO\left(S^2\right) = 0
\begin{aligned} SESGO(T) &= E[T] - \theta \\ SESGO(S^2) &= E\left[S^2\right] - \sigma^2 \\ &= E\left[\frac{1}{n-1} \sum_{i=1}^{n} \left(X_i - \bar{X}\right)^2\right] - \sigma^2 \\ &= E\left[\frac{1}{n-1} \sum_{i=1}^{n} X_i^2 - \frac{n}{n-1} \bar{X}^2\right] - \sigma^2 \\ &= \frac{1}{n-1} \sum_{i=1}^{n} E\left[X_i^2\right] - \frac{n}{n-1} E\left[\bar{X}^2\right] - \sigma^2 \\ &= \frac{1}{n-1} \, n \, \left(\sigma^2 + \mu^2\right) - \frac{n}{n-1} \left(\frac{\sigma^2}{n} + \mu^2\right) - \sigma^2 \\ &= \frac{n\sigma^2}{n-1} + \frac{n\mu^2}{n-1} - \frac{\sigma^2}{n-1} - \frac{n\mu^2}{n-1} - \frac{n-1}{n-1}\sigma^2 \\ &= \frac{n\sigma^2}{n-1} - \left(\frac{\sigma^2}{n-1} + \frac{n-1}{n-1}\sigma^2 \right) \\ &= \frac{n\sigma^2}{n-1} - \frac{n\sigma^2}{n-1} \\ &= 0 \end{aligned}
Concluimos que el estimador T = S^2 es insesgado para el parámetro \theta = \sigma^2. Lo cual explica en alguna medida, el porqué en la fórmula de la varianza muestral se divide por n-1, y no por n, como en el caso de la fórmula de la varianza poblacional.
10.2.3 Variabilidad (eficiencia)
Si T_1 y T_2 son dos estimadores insesgados para el mismo parámetro \theta, entonces el estimador con menor varianza naturalmente es mejor. Es decir, si Var[T_1] < Var[T_2], entonces T_1 es un mejor estimador del parámetro \theta que el estimador T_2.
Definición 10.5 (Eficiente) Un estimador insesgado T de un parámetro \theta es eficiente si su varianza Var[T] es la mínima varianza posible de todos los estimadores insesgados.
Si existe un estimador insesgado eficiente, entonces se dice que dicho estimador es un MVUE (Minimum Variance Unbiased Estimator).
La mínima varianza posible (teórica) para un estimador insesgado está determinada por algo denominado la cota de Cramér-Rao. Un estimador insesgado cuya varianza llega a ser igual a esa cota, automáticamente es un estimador insesgado eficiente (porque no puede haber un estimador insesgado con varianza menor que esa).
Ejemplo 10.4 Para una población con una distribución normal de media desconocida \theta = \mu y varianza conocida, se sabe que la cota de Cramér-Rao es \frac{\sigma^2}{n}.
Por otro lado, ya se hizo el desarrollo analítico que muestra que, Var\left[\bar{X}\right] = \frac{\sigma^2}{n}
De resultados presentados anteriormente, se tiene que \bar{X} es un estimador insesgado de \mu, cuya varianza coincide con la cota de Cramér-Rao (bajo las condiciones mencionadas). Por lo tanto, \bar{X} es un MVUE para \theta = \mu de una población con una distribución normal de varianza conocida.
En conclusión,
Para el parámetro proporción \left(\theta = p\right) de una población con una variable de interés con distribución Bernoulli, se sabe que el mejor estimador es la proporción muestral \left(T = \hat{P}\right).
Para el parámetro media \left(\theta = \mu\right) de una población con una variable de interés con distribución normal (asumiendo varianza poblacional conocida), se sabe que el mejor estimador es la media muestral media muestral \left(T = \bar{X}\right).
Para el parámetro varianza \left(\theta = \sigma^2\right) de una población con una variable de interés con distribución normal, se sabe que la misma fórmula poblacional pero con los datos muestrales (dividiendo por la cantidad de datos n) es sesgada, mientras que si divido por n-1 entonces es insesgada y es la que se denomina varianza muestral \left(T = S^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left(X_i - \bar{X}\right)^2\right)
10.2.3.1 Error Estándar
El error estándar (SE: Standard Error) de un estimador T es su desviación estándar, SE[T] = \sqrt{Var[T]} \; \Big(= SD[T] \Big)
El error estándar de \hat{P} es, SE\left[\hat{P}\right] = \sqrt{Var\left[\hat{P}\right]} = \sqrt{\frac{p(1-p)}{n}}
El error estándar estimado de \hat{P} sería, \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
El error estándar de \bar{X} (asumiendo varianza poblacional conocida) es, SE\left[\bar{X}\right] = \sqrt{Var\left[\bar{X}\right]} = \frac{\sigma}{\sqrt{n}}
10.2.4 Precisión
El error cuadrático medio (MSE: Mean Square Error) de un estimador T es, \begin{aligned} MSE[T] &= E\left[ \left( T - \theta \right)^2 \right] \\ &= Var\left[ T \right] + SESGO[T]^2 \end{aligned}
Podemos ver que el error cuadrático medio termina combinando en un solo resultado, ambos criterios mencionados (sesgo y variabilidad).
10.3 Ejercicios
Ejercicio 10.2
La siguiente información son datos obtenidos en una muestra aleatoria de las ventas de cinco meses:
Mes 1 2 3 4 5 Unidades vendidas 94 100 85 94 92
Calcule una estimación puntual de la media poblacional del número medio de unidades vendidas por mes.
Calcule una estimación puntual de la desviación estándar poblacional.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio 13.
Ejercicio 10.3
La American Association of Individuals Investors (AAII) realiza sondeos semanales entre sus suscriptores para determinar cuántos se muestran optimistas, pesimistas o indiferentes respecto del mercado de acciones a corto plazo. Sus hallazgos en la semana que terminó el 2 de marzo de 2006 son consistentes con los resultados muestrales siguientes (sitio web de AAII, 7 de marzo de 2006).
Optimistas: 409. Indiferentes: 299. Pesimistas: 291.
Proporcione una estimación puntual de los parámetros poblacionales siguientes.
Proporción de suscriptores de AAII que son optimistas respecto del mercado de acciones.
Proporción de suscriptores que son indiferentes al mercado de acciones.
Proporción de suscriptores que son pesimistas acerca del mercado accionario.
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 7. Ejercicio 17.
Ejercicio 10.4
En un estudio de USA Today/CNN/Gallup realizado con 369 padres que trabajan, se encontró que 200 consideran que pasan muy poco tiempo con sus hijos debido a sus compromisos laborales.
- Proporcione una estimación puntual de la proporción poblacional de padres que trabajan y piensan que pasan muy poco tiempo con sus hijos debido a sus compromisos laborales.
- ¿Cuál es el error estándar de la estimación puntual anterior?
Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 8. Ejercicio 54.
- No olvide seleccionar y resolver ejercicios (con respuesta) de un libro, acerca de lo visto en esta sección. Por ejemplo, aquellos ejercicios con respuesta entre los ejercicios 8.2 a 8.16 del libro de Walpole y los ejercicios 11 a 17 del capítulo 7 del libro de Anderson.