13 Juzgamiento
En esta sección se hará una revisión de algunos aspectos relacionados con el juzgamiento (prueba de hipótesis) acerca de un parámetro de interés, desde luego, bajo los supuestos asociados a las distribuciones muestrales previamente vistas.
13.1 Para empezar
- Lea todo el contenido de la presente sección (Inferencia, 13. Juzgamiento).
En sus propias palabras, haga una exposición escrita (como si le estuviera explicando a un compañero o amigo) acerca de lo que aprendió a partir de lo leído, incluya su discusión, reflexiones y conclusiones al respecto. Luego, exponga lo que no entendió e intente encontrar por su cuenta respuestas a las preguntas que le surgieron, para que las pueda compartir en clase.
13.2 Aspectos generales
Tengamos en cuenta la siguiente situación:
En una planta de producción, los recipientes deben quedar llenos con 16 onzas de producto. No está bien que se llenen de más ni de menos. Para evitar que eso ocurra, se revisa el sistema de llenado cada hora. Lo que se hace es tomar una muestra de 30 recipientes y revisar si el contenido sigue siendo cercano a 16 onzas, como debe ser. Si se aleja de 16, se interpreta como señal de que el sistema se desajustó y el operario debe parar la línea de producción para hacer la corrección. Se trabaja con un nivel de significancia de \alpha = 0.05 y se sabe, por datos históricos, que la desviación estándar del proceso es de 0.8 onzas. Plantee la prueba de hipótesis que permita decidir si es necesario detener la producción.
Adaptado de: Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 9. Ejercicio 60.
Una prueba de hipótesis es un procedimiento estadístico que se usa para tomar una decisión, con respecto a una conjetura acerca de la población, a partir de la evidencia que se tiene en la muestra (es decir, a partir de la información que nos da la muestra).
13.2.1 Hipótesis nula H_0 e hipótesis alternativa H_a
Suponga que se está en un juicio. Bajo la idea de que un acusado es inocente hasta que se demuestre lo contrario (el jurado debe encontrarlo culpable “más allá de la duda razonable”), entonces,
\begin{aligned} H_0 &: \text{ El acusado es inocente} \\ H_a &: \text{ El acusado es culpable} \end{aligned}
La evidencia tiene que ser suficiente para condenar al acusado (rechazar H_0). En caso contrario, se dice que no hay suficiente evidencia para declararlo culpable (no se rechaza H_0).
13.2.2 Tipo de error
| \, | H_0 es verdadera | H_a es verdadera |
|---|---|---|
| Se rechaza H_0 | Error Tipo I | \checkmark |
| No se rechaza H_0 | \checkmark | Error Tipo II |
Sea
\alpha = P[\text{Error Tipo I}]
y
\beta = P[\text{Error Tipo II}]
entonces \alpha se denomina el nivel de significancia y 1 - \beta la potencia de la prueba (usada para rechazar o no rechazar la hipótesis nula).
¿es posible que \alpha y \beta sean simultáneamente tan pequeños como uno quiera?
No, no es posible. Cuando reducimos uno de los dos, el otro aumenta.
Lo que si podemos hacer es fijar un valor relativamente pequeño para \alpha y utilizar pruebas que tengan la mayor potencia posible (pruebas con el menor \beta posible para ese \alpha fijo).
13.2.3 Pruebas de hipótesis a dos colas o a una cola
A dos colas:
\begin{aligned} H_0 &: \theta = \theta_0 \\ H_a &: \theta \neq \theta_0 \end{aligned}
A una cola a derecha:
\begin{aligned} H_0 &: \theta \leq \theta_0 \\ H_a &: \theta > \theta_0 \end{aligned}
A una cola a izquierda:
\begin{aligned} H_0 &: \theta \geq \theta_0 \\ H_a &: \theta < \theta_0 \end{aligned}
13.2.4 Pasos de una prueba de hipótesis
Determine la hipótesis nula H_0 y la hipótesis alternativa H_a.
Seleccione el estadístico de prueba apropiado
Calcule el valor que toma el estadístico a partir de los datos muestrales.
A partir de un nivel de significancia \alpha, usando:
el o los valores críticos:
- Determine el o los valores críticos y la regla de rechazo a partir de la distribución muestral del estadístico de prueba.
- Si el valor del estadístico de prueba está en la zona de rechazo entonces rechace H_0, en caso contrario no rechace H_0.
el p-valor:
- Calcule el p-valor correspondiente al valor del estadístico de prueba a partir de su distribución muestral.
- Si el p-valor es menor que \alpha entonces rechace H_0, en caso contrario no rechace H_0.
13.3 Una población
13.3.1 Media
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de la media de una población, es decir, en el caso en el cual el parámetro de interés \theta es la media \mu (H_0: \mu = \mu_0):
Si \sigma es conocida, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de la población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}}, la distribución muestral es \mathcal{N}(0,1), y,
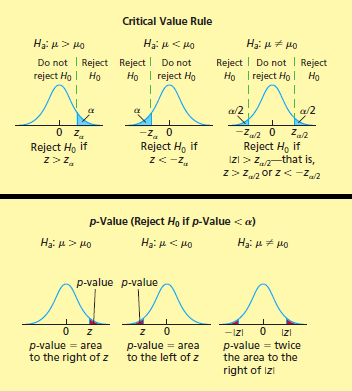
Si \sigma es desconocida, entonces, bajo el supuesto de que la variable de interés de la población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{\bar{x} - \mu_0}{s/\sqrt{n}}, la distribución muestral es t_{n-1}, y,
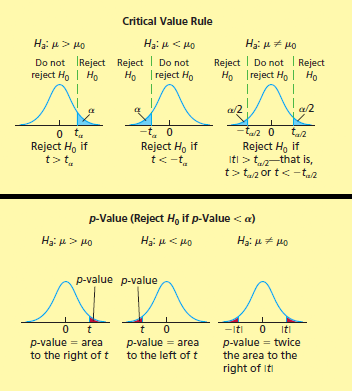
Para ilustrar:
Ejercicio 13.1
En una planta de producción, los recipientes deben quedar llenos con 16 onzas de producto. No está bien que se llenen de más ni de menos, porque eso genera problemas: a veces se desperdicia producto, otras veces los paquetes no cumplen con lo que se promete al cliente. Para evitar que eso ocurra, se revisa el sistema de llenado cada hora. Lo que se hace es tomar una muestra de 30 recipientes y revisar si el contenido sigue siendo cercano a 16 onzas, como debe ser. Si se aleja de 16, se interpreta como señal de que el sistema se desajustó y el operario debe parar la línea de producción para hacer la corrección. Se trabaja con un nivel de significancia de \alpha = 0.05 y se sabe, por datos históricos, que la desviación estándar del proceso es de 0.8 onzas.
- Plantee la prueba de hipótesis que permita decidir si es necesario detener la producción.
- Si en una cierta hora el promedio de la muestra resulta ser 16.32 onzas, ¿cuál es el valor-p?, ¿qué acción se debería tomar con base en ese resultado?
- Si en otra revisión el promedio muestral fue de 15.82 onzas, ¿cuál es el valor-p?, ¿qué acción se debe tomar?
Adaptado de: Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 9. Ejercicio 60.
Ejercicio 13.2 La asociación de comerciantes del centro histórico de Cartagena sostiene que el valor promedio del arriendo mensual de los locales comerciales en la zona no supera los 4.500.000 COP. Para evaluar esta afirmación, se analizó una muestra de 32 locales, con un arriendo promedio de 4.800.000 COP y una desviación estándar de 550.000 COP. Para un nivel de significancia de \alpha = 0.05, ¿la evidencia respalda la afirmación de la asociación?
13.3.2 Proporción
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de la proporción de una población, es decir, en el caso en el cual el parámetro de interés \theta es la proporción p (H_0: p = p_0), para n suficientemente grande (np > 10 y n(1-p) > 10), el valor del estadístico de prueba está dado por, \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} y la distribución muestral es \mathcal{N}(0,1).
Para ilustrar:
Ejercicio 13.3 Durante la Feria de Cali, una agencia de turismo afirma que al menos el 90\% de los hoteles estarán ocupados el fin de semana. Si al verificar 58 hoteles el sábado por la noche: 49 estaban a su capacidad máxima y 9 tenían habitaciones disponibles; con un nivel de significancia de \alpha = 0.05, ¿es posible respaldar la afirmación de la agencia?, ¿cuál es el valor-p?
13.3.3 Varianza
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de la varianza (o la desviación estándar) de una población, es decir, en el caso en el cual el parámetro de interés \theta es la varianza \sigma^2 (H_0: \sigma^2 = \sigma_0^2) (si el problema está planteado con la desviación estándar, eleve al cuadrado para llevarlo a un problema equivalente de varianza), bajo el supuesto de que la variable de interés de la población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{(n-1)s^2}{\sigma_0^2} y la distribución muestral es \chi^2_{n-1}
Para ilustrar:
Ejercicio 13.4 Se desea evaluar la estabilidad de los tiempos de viaje en un recorrido entre dos lugares. Durante 10 días se registraron los siguientes tiempos de viaje (en minutos): 44, 50, 40, 36, 30, 44, 48, 38, 52 y 55. ¿Existe evidencia suficiente para concluir que la desviación estándar de los tiempos de viaje es significativamente mayor a los 7 minutos? Utilice un nivel de significancia de 0.10 y suponga que la variable de interés sigue una distribución normal.
13.4 Dos poblaciones
13.4.1 Medias
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de las medias de dos poblaciones \mu_1 y \mu_2 (H_0: \mu_1 = \mu_2 + d_0), es decir, en el caso en el cual el parámetro de interés \theta es la diferencia de las medias \mu_1 - \mu_2 (H_0: \mu_1 - \mu_2 = d_0):
Si son observaciones pareadas, entonces haga:
X = X_1 - X_2 lo que implica que \bar{X} = \bar{X}_1 - \bar{X}_2 y \mu = \mu_1 - \mu_2, quedando así en la situación de una media de una población (para los anteriores X, \bar{X} y \mu).
Si NO son observaciones pareadas, con \sigma_1 y \sigma_2 conocidas, entonces, para n suficientemente grande o bajo el supuesto de que la variable de interés de cada población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{ \left( \bar{x}_1 - \bar{x}_2 \right) - \left( d_0 \right)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}, y la distribución muestral es \mathcal{N}(0,1).
Si NO son observaciones pareadas y se considera que \sigma_1 = \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{ \left( \bar{x}_1 - \bar{x}_2 \right) - \left( d_0 \right)}{s_p \, \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}, donde s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}, y la distribución muestral es t_{n_1+n_2-2}.
Si NO son observaciones pareadas y se considera que \sigma_1 \neq \sigma_2, entonces, bajo el supuesto de que la variable de interés de cada población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{ \left( \bar{x}_1 - \bar{x}_2 \right) - \left( d_0 \right)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}, y la distribución muestral es t_{\nu}, donde \nu = \left\lfloor \frac{\left(s_1^2/n_1+s_2^2/n_2\right)^2}{\frac{\left(s_1^2/n_1\right)^2}{n_1-1} + \frac{\left(s_2^2/n_2\right)^2}{n_2-1}} \right\rfloor.
Ejercicio 13.5
Durante la celebración del Día del Amor y la Amistad en Colombia, se quiso analizar si existe una diferencia significativa en el gasto promedio entre hombres y mujeres. En una muestra de 40 hombres, el gasto promedio fue de 105.700, mientras que en una muestra de 40 mujeres fue de 88.600. Estudios previos indican que la desviación estándar poblacional del gasto es de 25.000 para los hombres y 20.000 para las mujeres. ¿Apoyan los datos muestrales la hipótesis de que hay una diferencia significativa en el gasto promedio entre hombres y mujeres durante esta celebración?
Adaptado de: Anderson, Sweeney, Williams & Camm (2016). Estadística para Negocios y Economía. (12a. ed.) Cengage Learning. Capítulo 10. Ejercicio 5.
Ejercicio 13.6 En un estudio sobre hábitos de estudio, se comparó el tiempo semanal en horas que los estudiantes dedican a plataformas virtuales de aprendizaje versus métodos tradicionales (libros físicos y bibliotecas). Se recolectaron datos de 14 estudiantes:
| \, | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Virtuales | 12 | 5 | 14 | 13 | 8 | 15 | 12 | 10 | 11 | 13 | 9 | 9 | 8 | 10 |
| Tradicionales | 15 | 6 | 17 | 10 | 7 | 16 | 13 | 12 | 12 | 14 | 8 | 11 | 9 | 8 |
Use \alpha = 0.05 para probar si existe diferencia significativa entre las medias poblacionales de horas dedicadas a ambos métodos.
Ejercicio 13.7 En un estudio sobre movilidad urbana en Bogotá, se compararon dos aplicaciones móviles que ofrecen información sobre el transporte público de la ciudad. La App A ha estado en funcionamiento durante 6 años, mientras que la App B ha operado por 4 años. Los usuarios calificaron la precisión de los tiempos estimados de desplazamiento en una escala de 0 a 10, donde una calificación más alta indica mayor precisión percibida. Use \alpha = 0.05 para determinar si la aplicación con más años de operación tiene una calificación media poblacional mayor.
| App | n | \bar{x} | s |
|---|---|---|---|
| A | 24 | 9.0 | 0.73 |
| B | 15 | 8.2 | 0.82 |
Suponga primero que las varianzas poblacionales son iguales y luego repita el análisis sin asumir igualdad de varianzas.
13.4.2 Proporciones
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de las proporciones de dos poblaciones p_1 y p_2 (H_0: p_1 = p_2 + d_0), es decir, en el caso en el cual el parámetro de interés \theta es la diferencia de las proporciones p_1 - p_2 (H_0: p_1 - p_2 = d_0):
Si son observaciones pareadas, entonces haga
X = X_1 - X_2 lo que implica que \bar{X} = \hat{P}_1 - \hat{P}_2 y \mu = p_1 - p_2, quedando así en la situación de una media de una población (para los anteriores X, \bar{X} y \mu).
Si NO son observaciones pareadas y d_0 = 0 (H_0: p_1 = p_2 + 0), entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right), el valor del estadístico de prueba está dado por, \frac{ \left( \hat{p}_1 - \hat{p}_2 \right) - \left( 0 \right)}{ \sqrt{\hat{p} (1-\hat{p}) \left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}, donde \hat{p} = \frac{n_1 \hat{p}_1 + n_2 \hat{p}_2}{n_1 + n_2}, y la distribución muestral es \mathcal{N}(0,1).
Si NO son observaciones pareadas y d_0 \neq 0, entonces, para n suficientemente grade \left( n_1p_1>5 \right., n_2p_2>5, n_1(1-p_1)>5 y \left. n_2(1-p_2)>5 \right), el valor del estadístico de prueba está dado por, \frac{ \left( \hat{p}_1 - \hat{p}_2 \right) - \left( d_0 \right)}{\sqrt{\frac{\hat{p}_1\left(1-\hat{p}_1\right)}{n_1}+\frac{\hat{p}_2\left(1-\hat{p}_2\right)}{n_2}}} y la distribución muestral es \mathcal{N}(0,1).
Ejercicio 13.8 En una encuesta realizada en una universidad, se analizó si los estudiantes de Ingeniería usan más aplicaciones de productividad académica (de organización y gestión del tiempo, de colaboración y trabajo en grupo, de creación de contenido académico, etc.) que los estudiantes de Ciencias Económicas. De una muestra de 811 estudiantes de Ingeniería, 300 afirmaron usar estas aplicaciones regularmente, mientras que, de 750 estudiantes de Ciencias Económicas, 255 reportaron hacerlo. Pruebe la hipótesis de que los estudiantes de Ingeniería tienen una mayor propensión a utilizar aplicaciones de productividad académica que los de Ciencias Económicas, con un nivel de significancia de 0.05.
13.4.3 Varianzas
Si se desea hacer un juzgamiento (prueba de hipótesis) acerca de las varianzas (o las desviaciones estándar) de dos poblaciones \sigma_1^2 y \sigma_2^2 \left(H_0: \sigma_1^2 = d_0 \, \sigma_2^2\right), es decir, en el caso en el cual el parámetro de interés \theta es el cociente de las varianzas \sigma_1^2 y \sigma_2^2 \left(H_0: \frac{\sigma_1^2}{\sigma_2^2} = d_0\right) (si el problema está planteado con desviaciones estándar, eleve al cuadrado para llevarlo a un problema equivalente de cociente de varianzas), bajo el supuesto de que la variable de interés de la población tiene distribución normal, el valor del estadístico de prueba está dado por, \frac{1}{d_0} \frac{s_1^2}{s_2^2} y la distribución muestral es F_{n_1-1,n_2-1}.
Ejercicio 13.9 En un estudio realizado en una universidad, se analizó si los estudiantes que asistieron regularmente a las sesiones de tutoría de cierta asignatura obtuvieron mejores resultados en el examen final que aquellos que no asistieron. En una muestra de 50 estudiantes que asistieron a tutorías, la nota promedio fue de 3.95 con una desviación estándar de 0.3. En otra muestra de 50 estudiantes que no asistieron a tutorías, la nota promedio fue de 3.5 con una desviación estándar de 0.2. Plantee y pruebe la hipótesis de que, en promedio, los estudiantes que asisten a tutorías obtienen una nota 5 décimas mayor que quienes no asisten. Utilice un nivel de significancia de 0.01 y realice primero la prueba de igualdad de varianzas para decidir si debe asumir varianzas iguales o distintas.
13.5 Relación entre pruebas de hipótesis e intervalos de confianza
¿Existe una relación entre las pruebas de hipótesis y los intervalos de confianza?
Una prueba de hipótesis a dos colas (H_a: \theta \neq \theta_0) con un nivel de significancia \alpha es equivalente a calcular un intervalo de confianza bilateral del 100(1-\alpha)\% para \theta y rechazar H_0 si \theta_0 está por fuera del intervalo.
En general, la región de “no rechazo” es equivalente a (es la transformación de) un intervalo de confianza del parámetro de interés.
13.6 Otras pruebas de hipótesis
En general, las pruebas de hipótesis vistas hasta ahora suponen que la variable de interés en la población tiene una distribución aproximadamente normal, o en unos pocos casos bastó con suponer que se tiene una muestra suficientemente grande, lo cual nos permitió utilizar las distribuciones muestrales vistas en el Capítulo 11 (Distribuciones muestrales).
¿Qué hacer en caso de que la distribución de la variable de interés en la población: no es cuantitativa continua, no es simétrica, no es gaussiana por la razón que sea, y además no contamos con una muestra suficientemente grande para aplicar el teorema de límite central?
Algunas alternativas de juzgamiento (prueba de hipótesis), en donde no se hacen supuestos distribucionales, se pueden consultar en el Apéndice E (Juzgamiento no paramétrico)
13.7 Al finalizar
- No olvide seleccionar y resolver ejercicios de un libro, preferiblemente que tengan respuesta, acerca de lo visto en esta sección. Por ejemplo, seleccionar ejercicios del capítulo 10 (sin las secciones 10.6, 10.7, 10.11, 10.12 y 10.13) del libro de Walpole o de los capítulos 9, 10 y 11 (sin las secciones 9.7 y 9.8) del libro de Anderson.