6 Variables aleatorias
En esta sección se hará una revisión de algunos temas relacionados con variables aleatorias como lo son: la medida de probabilidad asociada a una variable aleatoria, las funciones de distribución acumulativas, las funciones de masa de probabilidad y de densidad, el valor esperado, la varianza, la desigualdad de Chebyshev y los cuantiles de una variable aleatoria.
- Lee todo el contenido de Apéndice, C Repaso: Cálculo integral.
- Lee todo el contenido de esta sección (Probabilidad, 6 Variables aleatorias).
- En tus propias palabras, has una exposición escrita detallada en tu cuaderno sobre cada parte de lo leído, como si le estuvieras explicando a un compañero o amigo. Recuerda que aprendemos aproximadamente el 95% de lo que tratamos de enseñar a otros.
- Anota cualquier duda o tema que te resulte confuso. ¡No te preocupes si no lo entiendes todo a la primera!
- Busca por tu cuenta respuestas a esas dudas. Esto te ayudará a llegar a clase con ideas para compartir.
- Lleva a clase: tu exposición escrita, tus dudas y las respuestas que encontraste. ¡Trabajaremos juntos para aclararlo todo!
En las secciones iniciales del material, en estadística descriptiva, hablamos de lo que eran las variables de los individuos de una población de interés.
Después, hablamos de probabilidad de un suceso o evento (es decir, probabilidad de un conjunto).
Mediante el concepto de variable aleatoria podemos unir esas dos cosas, y así poder hablar de la probabilidad de que una variable tome un cierto valor o conjunto de valores.
6.1 Definición
Sea X una variable asociada al “Número de puntos en la cara superior de un dado común de seis caras luego de lanzarlo una vez” o equivalentemente al “Resultado al lanzar, una vez, un dado común y corriente de seis caras”.
Evidentemente, los valores que puede llegar a tomar X son x = 1, 2, 3, 4, 5, 6. Además, se puede ver que la “variable” X resulta ser el objeto matemático representado por el siguiente gráfico:
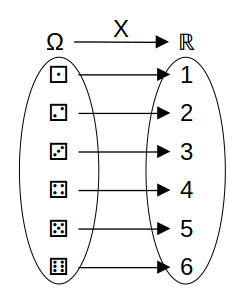
Definición 6.1 (Variable aleatoria) Una variable aleatoria es una función que asigna un número real a cada uno de los elementos del espacio muestral.
\begin{aligned} X : \Omega &\longrightarrow \mathbb{R} \\ \omega &\longrightarrow X(w) = x \in \mathbb{R} \end{aligned}
En otras palabras, una variable aleatoria es una representación o asociación numérica (en los números reales) para los resultados de un experimento aleatorio.
Ejercicio 6.1 Asocie una variable aleatoria a los siguientes experimentos aleatorios:
- Seleccionar un cliente al azar y que sea o no mayor de edad.
- Resultado de un partido (“ganar”, “perder”, “empatar”).
- Sacar una carta de un mazo (baraja).
Ejercicio 6.2
Sea W la variable aleatoria que da el número de caras menos el número de cruces en tres lanzamientos de una moneda. Liste los elementos del espacio muestral S para los tres lanzamientos de la moneda y asigne un valor w de W a cada punto muestral.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 3, Ejercicio 3.3.
Note como para las variables numéricas, su variable aleatoria asociada es bastante obvia.
W : “Número de hospitales de primer nivel en el municipio”
w = 0, 1, 2, 3, \dots
¿Cuál es la probabilidad de que un municipio seleccionado “al azar” tenga más de un hospital de primer nivel?
P[ \; W \qquad ¿? \qquad ]
Z : “Área del territorio municipal”
z > 0
¿Cuál es la probabilidad de que un municipio seleccionado “al azar” tenga un área de menos de mil kilómetros cuadrados?
P[ \; Z \qquad ¿? \qquad ]
En adelante las variables aleatorias se clasificarán en:
Discretas: Si el conjunto de posibles valores para X (la imagen de \Omega por X) es finito o infinito al estilo de los números enteros (infinito numerable).
Continuas: Si el conjunto de posibles valores para X (la imagen de \Omega por X) es infinito continuo al estilo de los número reales (infinito no numerable).
Ejercicio 6.3
Clasifique las siguientes variables aleatorias como discretas o continuas:
X: el número de accidentes automovilísticos que ocurren al año en Virginia.
Y: el tiempo para jugar 18 hoyos de golf.
M: la cantidad de leche que una vaca específica produce anualmente.
N: el número de huevos que una gallina pone mensualmente.
P: el número de permisos para construcción que los funcionarios de una ciudad emiten cada mes.
Q: el peso del grano producido por acre.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 3, Ejercicio 3.1.
6.2 Medida de probabilidad asociada
Recordemos, ¿qué objeto matemático es una medida de probabilidad P[\cdot]?
\begin{aligned} P : \wp (\Omega) &\longrightarrow [0,1] \\ A &\longrightarrow P[A] = p \\ \\ A \subseteq \Omega &\qquad 0 \leq p \leq 1 \end{aligned}
Es lógico querer una manera de obtener probabilidades para un conjunto B de potenciales valores x en los reales, que podría tomar la variable aleatoria X.
Es decir quisiera una medida de probabilidad P_X tal que:
\begin{aligned} P_X : \mathcal{B} (\mathbb{R}) &\longrightarrow [0,1] \\ B &\longrightarrow P_X[B] = p \in [0,1] \end{aligned}
¿Cómo podríamos usar lo que ya hemos visto para lograr lo que queremos o necesitamos?
Ya tenemos una X y una P tal que,
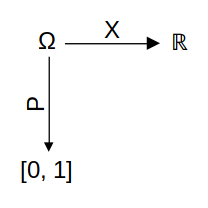
Además, recordemos que,
Imagen: Sea A \subset \Omega, la imagen de A por X es X(A) = \{x \in \mathbb{R}: X(\omega) = x \text{, para algún } \omega \in A\}
Preimagen: Sea B \subset \mathbb{R}, la preimagen de B por X es X^{-1}(B) = \{\omega \in \Omega: x = X(\omega) \text{, para algún } x \in B\}
Entonces, se puede definir la probabilidad de que la variable aleatoria X tome un subconjunto de valores en los reales B de la siguiente manera:
\begin{aligned} P_X[B] &= P_X[\{ x: x \in B \}] \\ &= P[\{ \omega \in \Omega: X(w) = x \text{, para algún } x \in B \}] \\ &= P[X^{-1}(B)] \end{aligned}
Es decir, obtenemos P_X haciendo la composición de X^{-1} y P.
Además, P_X cumple todos los axiomas, y por ende todas las propiedades, de una medida de probabilidad.
Lo único que cambia con respecto a lo anteriormente visto acerca de probabilidades es que siempre estaremos trabajando con conjuntos en los números reales, en vez de estar trabajando con conjuntos de espacios muestrales distintos que dependen del experimento aleatorio.
Abusando un poco de la notación, siempre utilizaremos P[X \in B] para referirnos a P_X[B].
Lo cual implica que,
Si B = \{a\} entonces \begin{aligned} P_X\big[\{a\}\big] &= P\Big[X^{-1}\big(\{a\}\big)\Big] \\ &= P\big[X \in \{a\}\big] \\ &= P[X=a] \end{aligned}
Si B = (a,b] entonces \begin{aligned} P_X\big[(a,b]\big] &= P\Big[X^{-1}\big((a,b]\big)\Big] \\ &= P\big[X \in (a,b]\big] \\ &= P[a < X \leq b] \end{aligned}
En los siguientes ejercicios, reescriba la probabilidad solicitada en términos de la variable aleatoria usando la notación indicada, y si es posible obtenga el valor para dicha probabilidad.
Ejercicio 6.4 Sea X := “Número que aparece en la cara superior de un dado después de ser lanzado una vez”.
P[\text{``Sacar más de 4''}] = \text{¿?}
Ejercicio 6.5 Se sabe que una línea de producción opera con seis máquinas trabajando simultáneamente.
Sea X := “Número de la máquina que procesó un producto terminado seleccionado aleatoriamente, según el orden de instalación y registro de la máquina”.
¿Cómo escribiría con símbolos, en términos de X, la probabilidad de que un producto terminado seleccionado aleatoriamente haya sido procesado por una de las tres últimas máquinas según el orden de instalación y registro de las mismas?
¿Cambia la expresión solicitada dependiendo de si la carga de trabajo está distribuida equitativamente entre las máquinas? (adicionalmente, reflexione sobre cómo podría afectar esto al valor de dicha probabilidad).
Ejercicio 6.6 Sea Y := “El resultado de un partido codificado de la siguiente manera: Ganar=1, Empatar=0, Perder=-1”.
P[\text{``No perder''}] = \text{¿?}
Ejercicio 6.7 Sea Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.
P[\text{``Sacar al menos dos sellos''}] = \text{¿?}
Ejercicio 6.8 Se sabe que una línea de producción opera con dos máquinas trabajando simultáneamente.
Sea X := “Número de productos terminados que fueron procesados por la máquina 1, de tres que fueron seleccionados aleatoriamente”.
¿Cómo escribiría con símbolos, en términos de X, la probabilidad de que al menos dos de los tres productos seleccionados hayan sido procesados por la máquina 2?.
¿Cambia la expresión solicitada dependiendo de si los productos fueron seleccionados con reemplazo o sin reemplazo? (adicionalmente, reflexione sobre cómo podría afectar esto al valor de dicha probabilidad).
6.3 Funciones importantes para una v.a.
6.3.1 Para una v.a. discreta
La función de masa de probabilidad \left(f(x)\right) (de una variable aleatoria discreta) se puede ver como la tabulación de todas las probabilidades relevantes.
La función de masa de probabilidad f_X de una variable aleatoria discreta X se podría definir como: \begin{aligned} f_X(x) &= P[X=x] \end{aligned} donde x \in \mathbb{R}.
Para que una función (f_X) sea una función de masa de probabilidad, de una variable aleatoria discreta X, debe cumplir lo siguiente:
- f_X(x) \geq 0, para todo x \in \mathbb{R}.
- \sum\limits_{t \in \mathbb{R}} f_X(t) = 1.
Ejercicio 6.9
Determine el valor c de modo que cada una de las siguientes funciones sirva como distribución de probabilidad de la variable aleatoria discreta X:
f_X(x) = c \left( x^2 + 4 \right), para x = 0, 1, 2, 3;
f_X(x) = c \binom{2}{x} \binom{3}{3 - x}, para x = 0, 1, 2.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 3, Ejercicio 3.5.
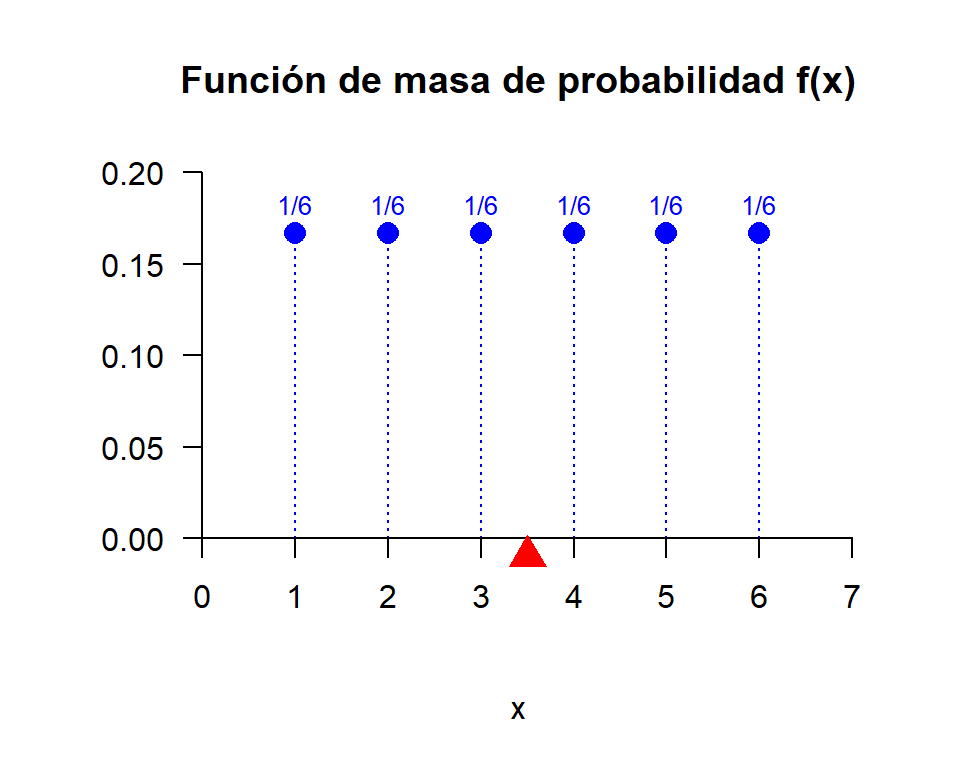
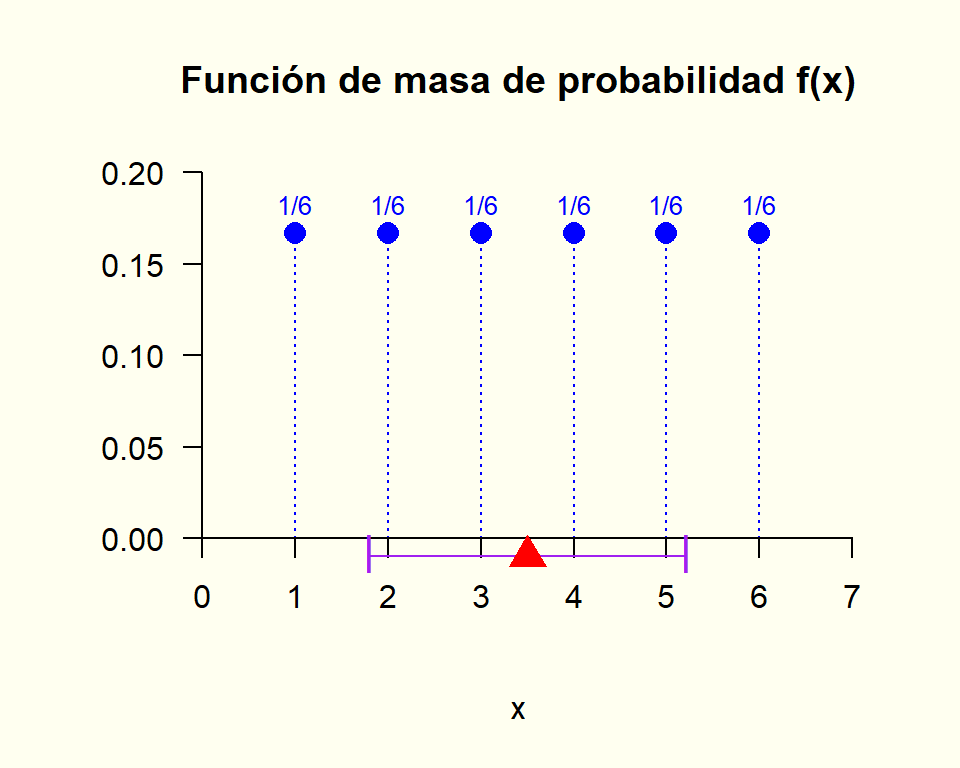
Ejercicio 6.10 Determine y haga el gráfico de la función de masa de probabilidad asociada a la siguiente variable aleatoria:
X := “Resultado al lanzar, una vez, un dado común y corriente”.
Valores que toma la variable aleatoria X:
x = 1, 2, 3, 4, 5, 6.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| f_X(x) = P[X=x] | \frac{1}{6} | \frac{1}{6} | \frac{1}{6} | \frac{1}{6} | \frac{1}{6} | \frac{1}{6} |
¿Cómo hallar cualquier probabilidad deseada, a partir de la función de masa de probabilidad?
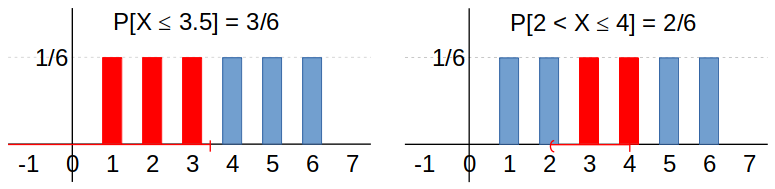
Si se conoce la función de masa de probabilidad de una variable aleatoria, entonces,
\begin{aligned} P[X \in B] &= \sum\limits_{t \in B} f_X(t) \\ \\ P[a < X \leq b] &= \sum\limits_{a < t \leq b} f_X(t) \\ \\ P[a \leq X < b] &= \sum\limits_{a \leq t < b} f_X(t) \\ \\ \vdots \end{aligned}
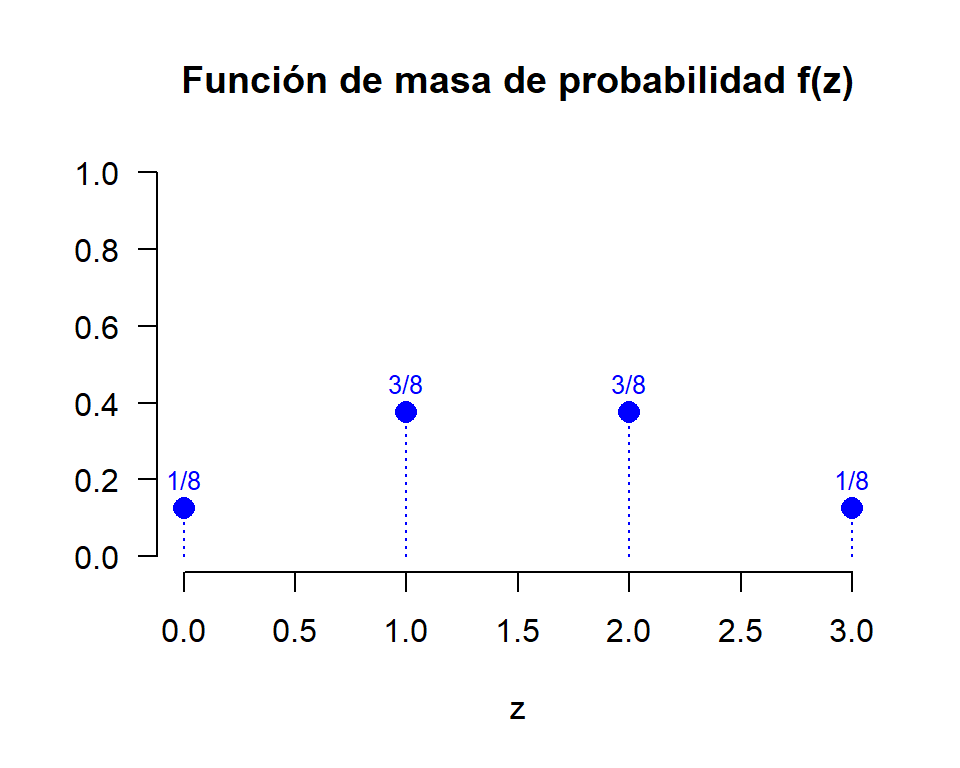
Ejercicio 6.11 Determine y haga el gráfico de la función de masa de probabilidad asociada a la siguiente variable aleatoria:
Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.
Valores que toma la variable aleatoria Z:
z = 0, 1, 2, 3.
| x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| f_X(x) = P[X=x] | \frac{1}{8} | \frac{3}{8} | \frac{3}{8} | \frac{1}{8} |
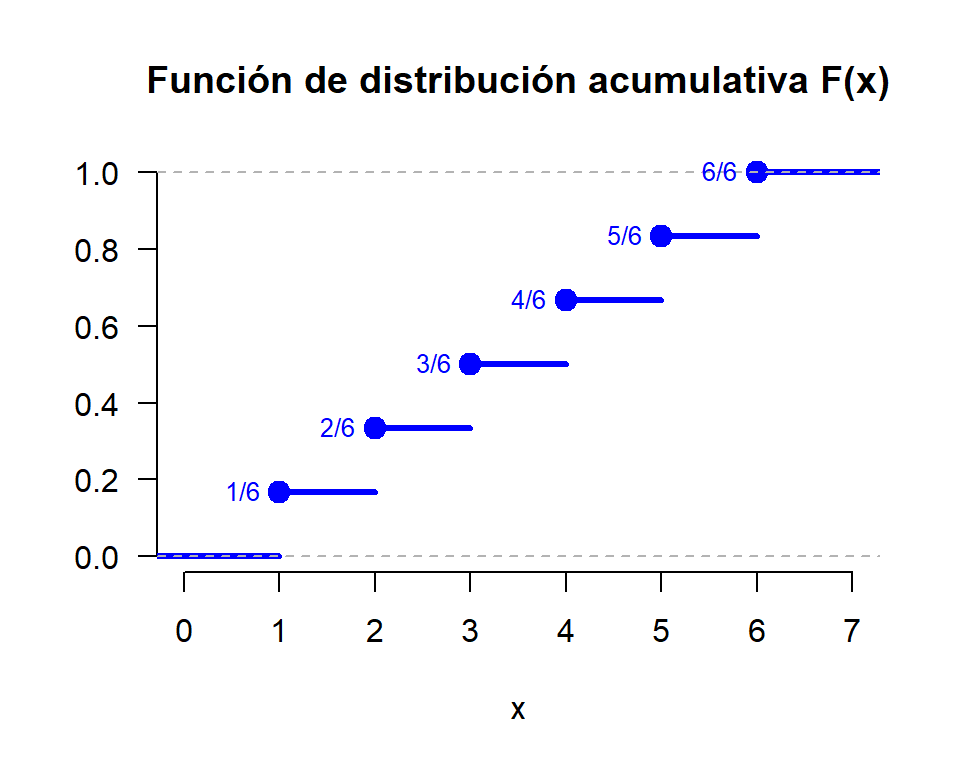
La función de distribución acumulativa \left(F(x)\right) es la probabilidad que llevo acumulada hasta cierto valor sobre el eje x.
La función de distribución acumulativa F_X de una variable aleatoria X se define como: \begin{aligned} F_X(x) &= P \big[ X \in (-\infty,x] \big] \\&= P[ X \leq x ] \end{aligned} donde x \in \mathbb{R}.
Para que una función (F_X) sea una función de distribución acumulativa, de una variable aleatoria X, debe cumplir lo siguiente:
- F_X es no decreciente (Si x_1 \leq x_2 entonces F_X(x_1) \leq F_X(x_2)).
- F_X es continua a derecha \left( F_X(x^+) = \lim\limits_{h \to 0} F_X(x + h) = F_X(x) \right).
- F_X tiende a cero cuando x tiende a menos infinito \left( \lim\limits_{x \to -\infty} F_X(x) = 0 \right).
- F_X tiende a uno cuando x tiende a infinito \left(\lim\limits_{x \to \infty} F_X(x) = 1\right).
Ejercicio 6.12 Determine y haga el gráfico de la función de distribución acumulativa asociada a la siguiente variable aleatoria:
X := “Resultado al lanzar, una vez, un dado común y corriente”.
Valores que toma la variable aleatoria X:
x = 1, 2, 3, 4, 5, 6.
La función de distribución acumulativa asociada a la variable aleatoria X es,
F_X(x) = \begin{cases} \frac{0}{6}=0 & \text{si } x < 1 \\ \frac{1}{6} & \text{si } 1 \leq x < 2 \\ \frac{2}{6} & \text{si } 2 \leq x < 3 \\ \frac{3}{6} & \text{si } 3 \leq x < 4 \\ \frac{4}{6} & \text{si } 4 \leq x < 5 \\ \frac{5}{6} & \text{si } 5 \leq x < 6 \\ \frac{6}{6}=1 & \text{si } 6 \leq x \end{cases}
y su gráfico sería,

¿Cómo hallar cualquier probabilidad deseada, a partir de la función de distribución acumulativa?
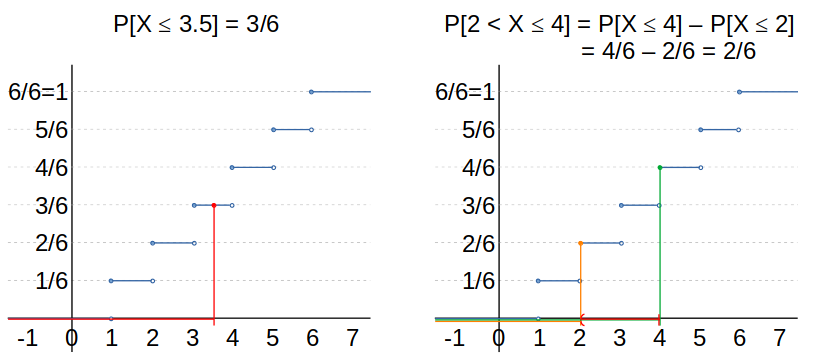
Si se conoce la función de distribución acumulativa de una variable aleatoria, entonces se puede calcular cualquier probabilidad que se nos pueda ocurrir:
\begin{aligned} P[X \leq b] &= F_X(b) \\ \\ P[X < b] &= \lim\limits_{h \to 0} F_X(b-h) \\&= F_X(b^-) \\ \\ P[a < X \leq b] &= P[X \leq b] - P[X \leq a] \\&= F_X(b) - F_X(a) \\ \\ P[a \leq X < b] &= P[X < b] - P[X < a] \\&= F_X(b^-) - F_X(a^-) \\ \\ P[a < X < b] &= P[X < b] - P[X \leq a] \\&= F_X(b^-) - F_X(a) \\ \\ P[a \leq X \leq b] &= P[X \leq b] - P[X < a] \\&= F_X(b) - F_X(a^-) \\ \\ P[X = a] &= P[a \leq X \leq a] \\&= P[X \leq a] - P[X < a] \\&= F_X(a) - F_X(a^-) \end{aligned}
Ejercicio 6.13 Determine y haga el gráfico de la función de distribución acumulativa asociada a la siguiente variable aleatoria:
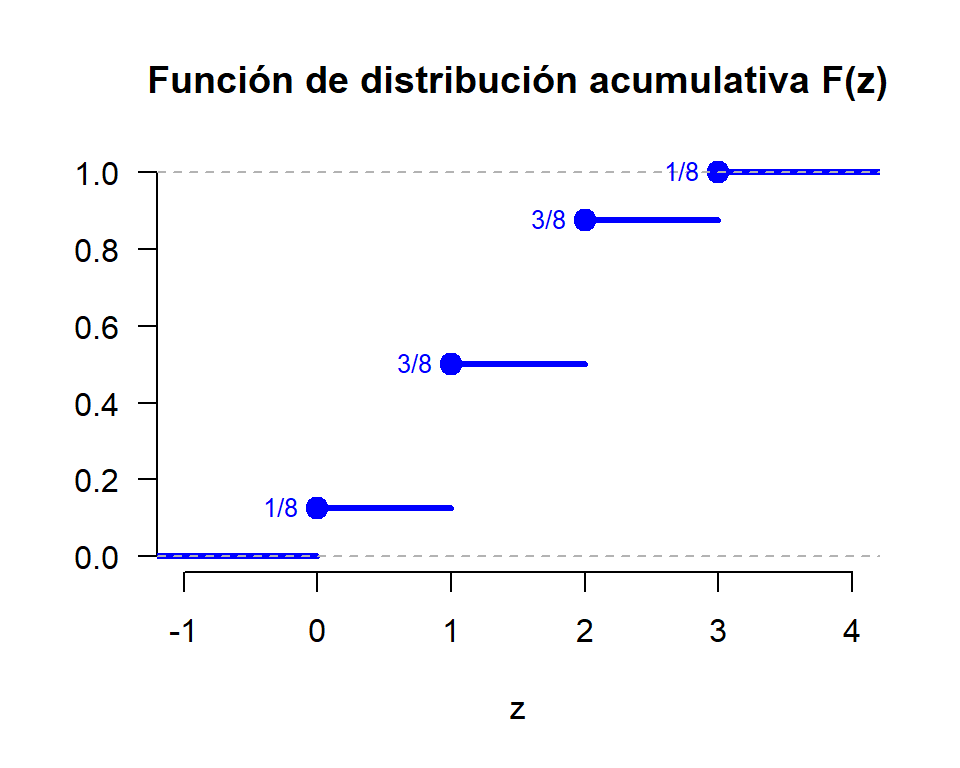
Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”.
Valores que toma la variable aleatoria Z:
z = 0, 1, 2, 3.
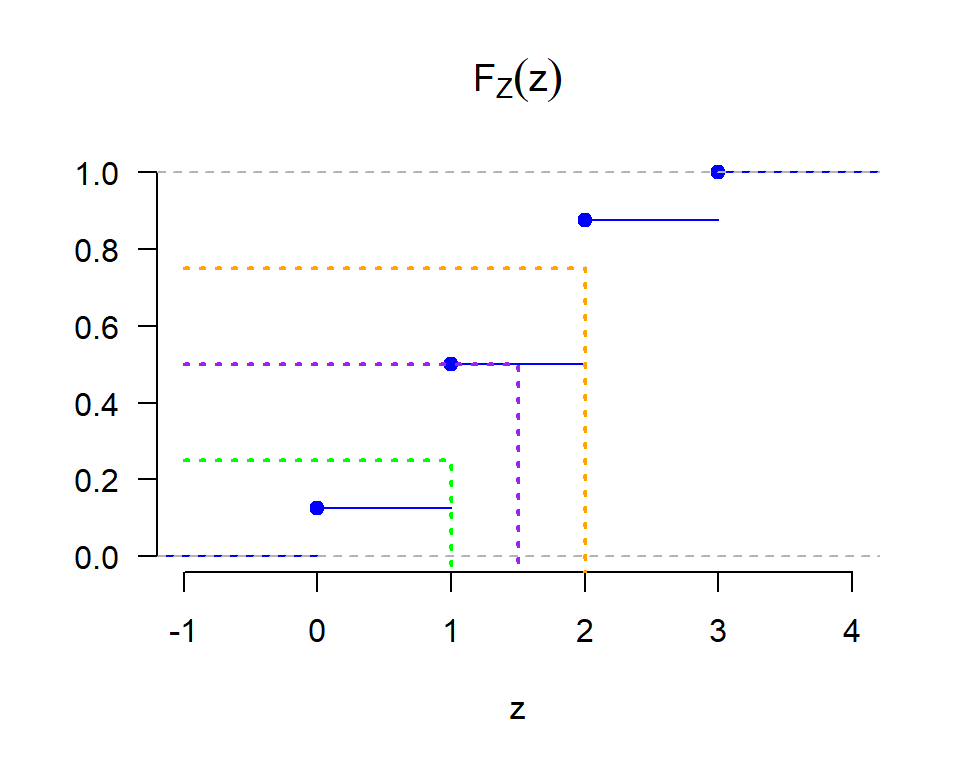
F_Z(z) = \begin{cases} \frac{0}{8} = 0 & \text{si } z < 0 \\ \frac{1}{8} & \text{si } 0 \leq z < 1 \\ \frac{4}{8} & \text{si } 1 \leq z < 2 \\ \frac{7}{8} & \text{si } 2 \leq z < 3 \\ \frac{8}{8} = 1 & \text{si } 3 \leq z \end{cases}
Ejercicio 6.14 Determine y haga el gráfico de la función de distribución acumulativa F_X(x) asociada a la variable aleatoria X := “Número de hijos de una familia-hogar seleccionado aleatoriamente (suponiendo que todas las familias-hogares tienen la misma oportunidad de ser seleccionadas), de una población en donde se tiene lo que aparece en la siguiente tabla.”
| \, | f. abs. | f. rel. | f. abs. acum. | f. rel. acum. |
|---|---|---|---|---|
| 0 | 301 | 0.301 | 301 | 0.301 |
| 1 | 183 | 0.183 | 484 | 0.484 |
| 2 | 270 | 0.270 | 754 | 0.754 |
| 3 | 155 | 0.155 | 909 | 0.909 |
| 4 | 91 | 0.091 | 1000 | 1 |
| Total | 1000 | 1 | No aplica | No aplica |
Ejercicio 6.15
La distribución de probabilidad de X, el número de imperfecciones que se encuentran en cada 10 metros de una tela sintética que viene en rollos continuos de ancho uniforme, está dada por
x 0 1 2 3 4 f(x) 0.41 0.37 0.16 0.05 0.01 Construya la función de distribución acumulativa de X.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 3, Ejercicio 3.13.
Además, calcule la probabilidad de que uno de los rollos presente entre 1 y 3 imperfecciones (incluidos los valores 1 y 3):
usando la función de distribución acumulativa de X;
utilizando la función de masa de probabilidad de X.
A manera de conclusión, note la forma en que están relacionadas una función de distribución acumulativa (F) y su respectiva función de masa de probabilidad (f) (para un v.a. discreta).
\begin{aligned} F_X(x) &= P[ X \leq x ] \\ &= \sum\limits_{t \leq x} P \big[ X = t \big] \\ F_X(x) &= \sum\limits_{t \leq x} f_X(t) \end{aligned}
\begin{aligned} f_X(x) &= P[ X = x ] \\ &= P[ x \leq X \leq x ] \\ &= P[X \leq x] - P[X < x] \\ f_X(x) &= F_X(x) - F_X(x^-) \end{aligned}
¿Qué cosas cambiaran, qué cosas serán similares y qué cosas serán idénticas para las variables aleatorias continuas, con respecto a las que acabamos de ver para las variables aleatorias discretas?
6.3.2 Para una v.a. continua
Sea una variable aleatoria X definida como el tiempo que toca esperar para que ocurra un cierto evento (por ejemplo, el tiempo que una persona debe esperar a un familiar o amigo en un punto de encuentro).
Supongamos que una persona errónea o incorrectamente considera la variable como discreta, con valores posibles x = 1, 2, \dots, 15 minutos, todos igualmente probables. En ese caso:
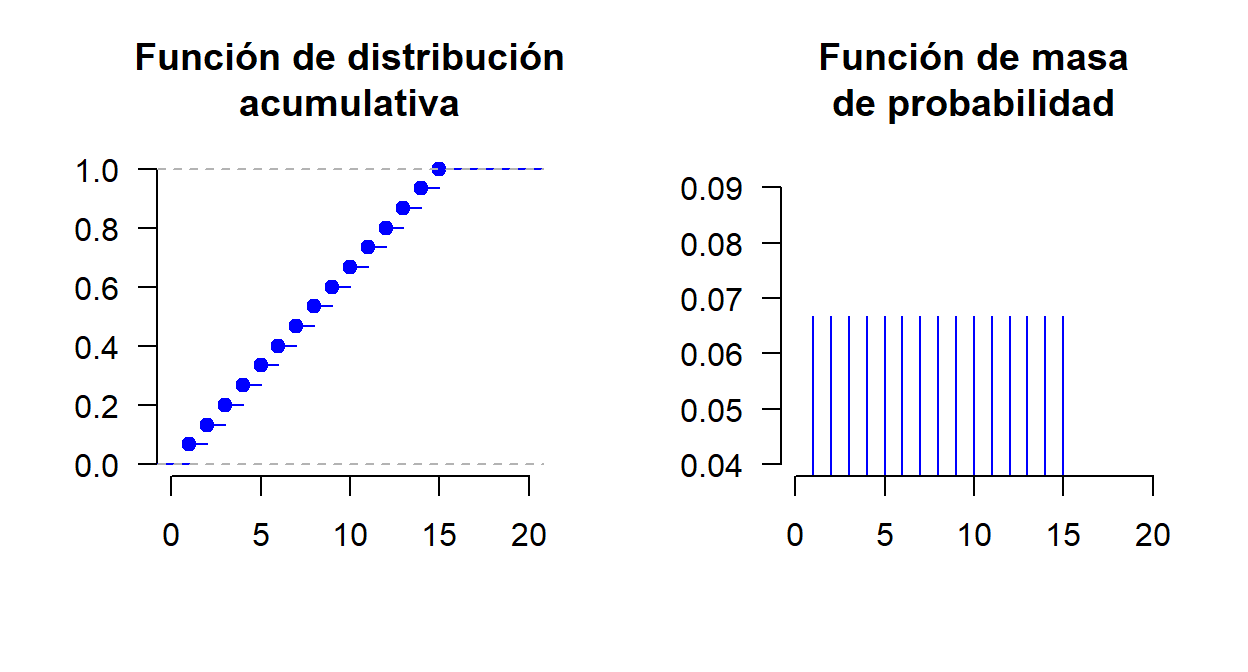
Ahora, supongamos que esta persona empieza a notar que algo no encaja, e intenta corregir el error pasando de minutos a segundos.
Asume entonces, también de forma incorrecta, que la variable aleatoria es discreta con valores x=1,2,\dots,900 segundos, todos igualmente probables. En ese caso:
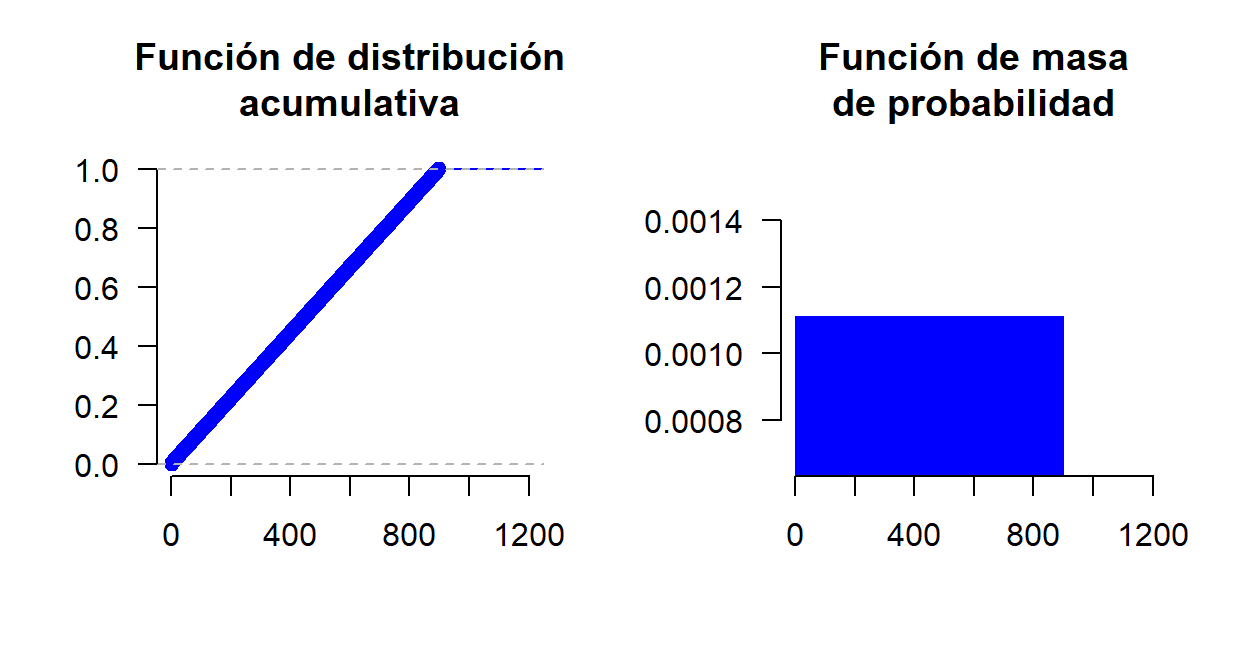
Finalmente, la persona se da cuenta de que el verdadero error es haber tratado como discreta una variable que en realidad es continua.
Desde estadística descriptiva ya sabemos que una variable asociada al tiempo es cuantitativa continua, con escala de razón.
No obstante, gracias al error cometido, podemos imaginar qué ocurre al dividir el tiempo en unidades cada vez más pequeñas, hasta llegar a valores infinitesimales.
El tiempo de espera puede variar infinitesimalmente entre 0 y 15 minutos (0<x<15), con igual probabilidad. En ese caso:
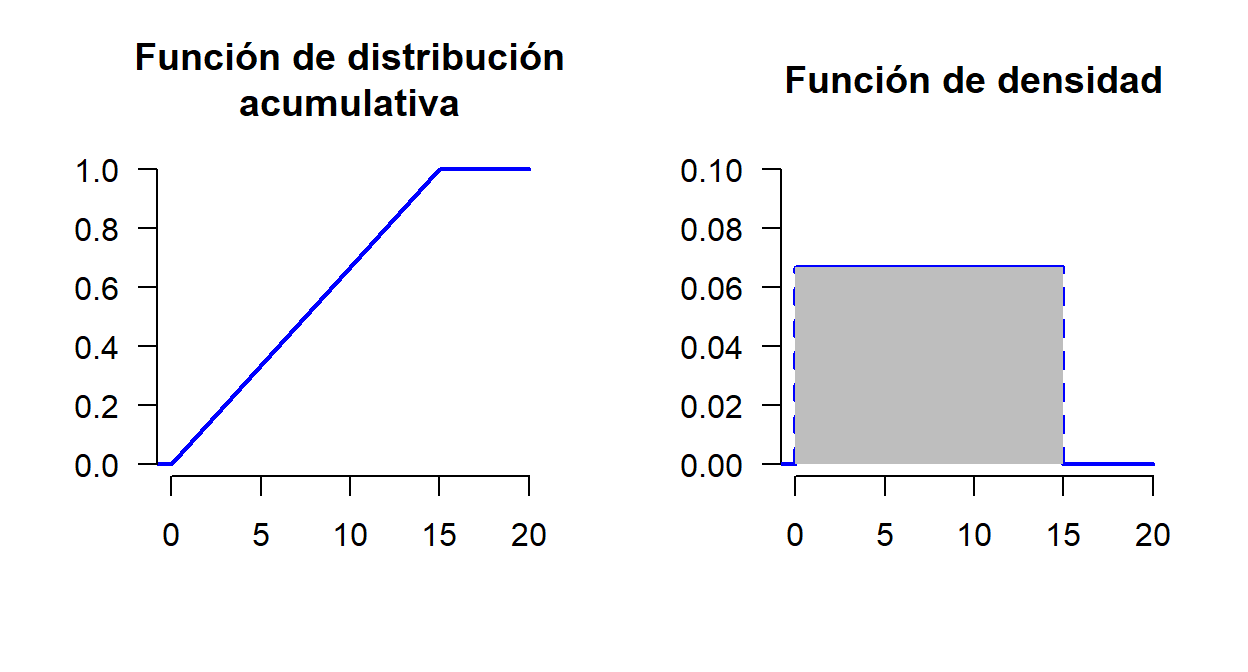
Si para una variable aleatoria discreta se tiene que f_X(x) := F_X(x) - F_X(x^-), entonces ¿cual sería la fórmula equivalente (infinitesimal) para una aleatoria continua?
La función de densidad f_X de una variable aleatoria continua X se define como: \begin{aligned}f_X(x) &= \lim_{\Delta x \to 0^+} \frac{F_X(x) - F_X(x-\Delta x)}{x - (x-\Delta x)} \\ &=\frac{d}{dx} F_X(x^-) \\ &= F'_X (x^-)\end{aligned}
Es evidente que en este punto son y serán muy importantes varios aspectos relacionados con el proceso de derivación de funciones, pero sobretodo con el proceso inverso, el proceso de antiderivación / integración.
En el Apéndice C hay una pequeña y rápida revisión de algunos aspectos básicos relacionados con la integración de funciones (Revisión básica: Cálculo integral).
Una función f_X es función de densidad de una variable aleatoria continua X si:
- f_X(x) \geq 0, para todo x \in \mathbb{R}.
- \int\limits_{t \in \mathbb{R}} f_X(t) \, dt = \int\limits_{-\infty}^{\infty} f_X(t) \, dt = 1
Cualquier función, que nunca tome valores negativos (es decir, f(x) \geq 0 para todo x \in \mathbb{R}), y cuya área total bajo la curva sea igual a 1 (es decir, \int_{\mathbb{R}} f(x) \, dx = 1), puede ser utilizada como una función de densidad de probabilidad.
Ejercicio 6.16 Sea una variable aleatoria continua X de su interés (podría ser la variable aleatoria definida como “el tiempo que toca esperar…”).
Supongamos que la variable solamente puede tomar valores entre 0 y 1 (en el caso de la variable “tiempo que toca esperar…”, podría querer decir que se espera máximo una hora, un día o uno (1) de cualquier otra unidad de tiempo.
También podríamos estar hablando de una variable “proporción…”, por ejemplo “proporción de los ingresos de una persona o un hogar que se gastan en turismo”).
Supongamos que su función de densidad está dada por: f_X(x) = \begin{cases} c(3 - 3x^2) & \text{si } 0 < x < 1 \\ 0 & \text{en otro caso} \end{cases}
Para que f_X(x) efectivamente sea una función de densidad, ¿cuál debería ser el valor de c?
Note que,
\begin{aligned} F_X(x) &= P[X \leq x] \\ &= \int\limits_{-\infty}^x f_X(t) \, dt \end{aligned}
Es decir que P[X \leq x] es igual al área acumulada bajo la curva y = f_X(t) desde -\infty hasta el valor dado para x.
La función de distribución acumulativa \left(F(x)\right) es el área (es decir, la probabilidad) que llevo acumulada hasta cierto valor sobre el eje x.
Ejercicio 6.17 Encuentre la correspondiente función de distribución acumulativa de la variable aleatoria X del Ejercicio 6.16
Si se conoce la función de densidad de una variable aleatoria, entonces,
\begin{aligned} P[X \in B] &= \int\limits_{t \in B} f_X(t) dt \\ \\ P[a \leq X \leq b] &= \int\limits_{a \leq t \leq b} f_X(t) dt \\&= \int\limits_{a}^{b} f_X(t) dt \end{aligned}
Es decir que P[a \leq X \leq b] es igual al área bajo la curva dada por f_X(t), entre las rectas x=a y x=b.
Ejercicio 6.18 Para la variable aleatoria X del Ejercicio 6.16, calcule:
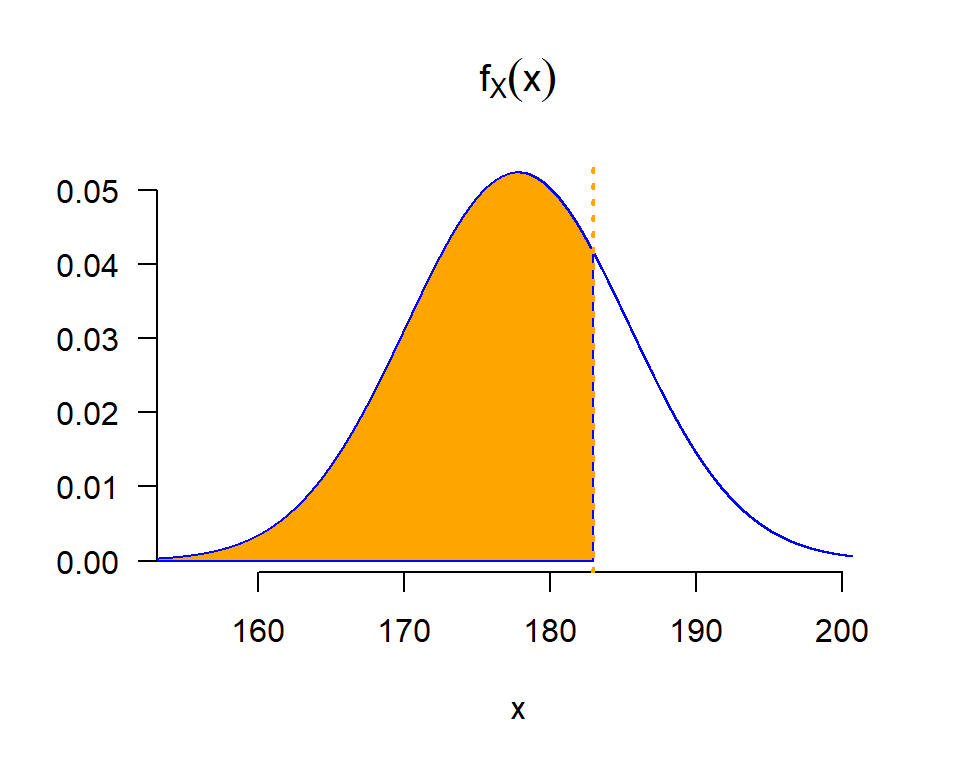
- P[X < 0.2] (probabilidad de “que en una ocasión se tenga que esperar menos de 0.2 horas (12 minutos)” o “de que en un hogar se gaste en turismo menos del 20\% de sus ingresos”).
- P[X \geq 0.7].
- P[0.4 < X < 0.6].
- P[X = 0.5].
Si X una variable aleatoria continua, entonces P[X=a] = ¿?.
Ejercicio 6.19
El número total de horas, medidas en unidades de 100 horas, que una familia utiliza una aspiradora en un periodo de un año es una variable aleatoria continua X que tiene la siguiente función de densidad: f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Calcule la probabilidad de que en un periodo de un año una familia utilice su aspiradora,
menos de 120 horas;
entre 50 y 100 horas.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 3, Ejercicio 3.7.
Ejercicio 6.20
El tiempo que pasa, en horas, para que un radar detecte entre conductores sucesivos a los que exceden los límites de velocidad es una variable aleatoria continua con una función de distribución acumulativa F(x) = \begin{cases} 0, & x < 0, \\ 1 - e^{-8x}, & x \geq 0, \end{cases} Calcule la probabilidad de que el tiempo que pase para que el radar detecte entre conductores sucesivos a los que exceden los límites de velocidad sea entre 12 y 30 minutos,
utilizando la función de densidad de probabilidad de X.
usando la función de distribución acumulativa de X;
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 3.14.
LLegamos a las siguientes conclusiones:
Basta con conocer la función de distribución acumulativa o la función de masa de probabilidad de una variable aleatoria discreta (la función de densidad en el caso de una variable aleatoria continua), para conocer por completo el mecanismo aleatorio que rige a la variable y a su correspondiente experimento aleatorio. Por lo tanto, si tengo cualquiera de estas dos funciones, entonces puedo calcular cualquier probabilidad que desee.
También podemos concluir que las tablas de frecuencias relativas y relativas acumuladas nos están dando la función de masa de probabilidad y la función de distribución acumulativa correspondiente a la variable aleatoria más simple de obtener a partir de una variable de interés de una tabla de datos (la v.a. asociada a la selección de un solo individuo al azar).
Para las variables aleatorias continuas, se “teorizará” acerca de las funciones que rigen la variable y se supondrá que la variable tiene una cierta función de densidad o de distribución acumulativa.
Por otra parte, la clasificación de una variable aleatoria también se puede determinar a partir de las características de la función de distribución acumulativa:
Discretas: Cuando F_X (una función de distribución acumulativa válida) es una función escalonada.
Continuas: Cuando F_X (una función de distribución acumulativa válida) es una función continua.
Mixtas: Cuando F_X (una función de distribución acumulativa válida) es una combinación de al menos una parte escalonada y una parte continua.
6.4 Valor esperado o esperanza
Suponga que un distribuidor de joyería antigua está interesado en comprar un collar de oro para el que tiene 0.22 de probabilidades de venderlo con $250 de utilidad; 0.36 de venderlo con $150 de utilidad; 0.28 de venderlo al costo y 0.14 de venderlo con una pérdida de $150. ¿Cuál es su utilidad esperada?
Tomado de: Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 4.8.
El valor esperado / la esperanza / el promedio para una variable aleatoria discreta X es: \begin{aligned} \mu_X &= E[X] \\ &= \sum_{t \in \mathbb{R}} t \, f_X(t) \\ &= \sum_{t \in \mathbb{R}} t \, P[X=t] \end{aligned}
El valor esperado / la esperanza / el promedio para una variable aleatoria continua X es: \begin{aligned} \mu_X &= E[X] \\ &= \int_{t \in \mathbb{R}} t \, f_X(t) \, dt \\ &= \int_{-\infty}^{\infty} t \, f_X(t) \, dt \end{aligned}
Supongamos que la utilidad en la compra de un collar de oro esta dada los valores continuos que puede tomar un x (por ejemplo, -150 < x < 250) y que las probabilidades asociadas a esos valores continuos de x están asociadas a una función de densidad f(x), entonces el promedio (media, valor esperado o esperanza) de la utilidad sería el área total bajo la curva de la función h(t) = (t) \big( f(t) \big) (el área por debajo del eje t tiene signo negativo).
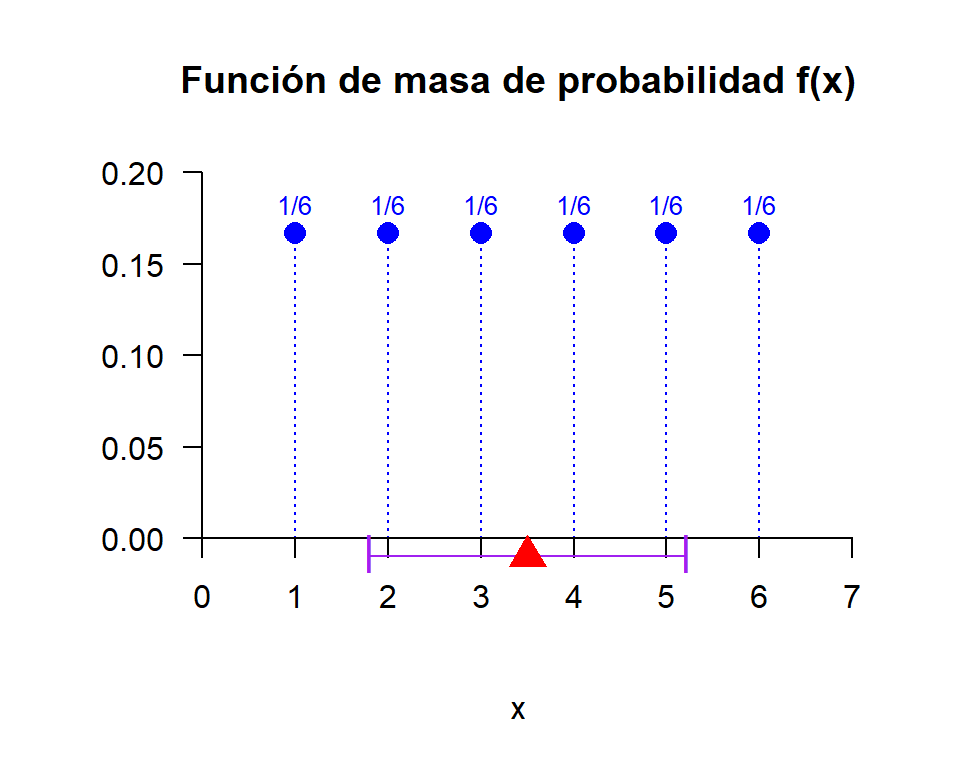
El promedio (media, valor esperado o esperanza) de una variable aleatoria se puede interpretar como punto de equilibrio.
Propiedades del valor esperado:
- Si X = a constante, entonces E[X] = E[a] = a.
- E[X + b] = E[X] + b.
- E[a \, X] = a \, E[X].
Ejercicio 6.21 Encuentre el valor esperado / la esperanza / el promedio del número de puntos que aparecen en la cara superior de un dado común y corriente de seis caras que se lanza una vez.
X := “Resultado al lanzar, una vez, un dado común y corriente”.
Valores que toma la variable: x = 1, 2, 3, 4, 5, 6.
| x | f_X(x) | x \, f_X(x) |
|---|---|---|
| 1 | \frac{1}{6} | \frac{1}{6} |
| 2 | \frac{1}{6} | \frac{2}{6} |
| 3 | \frac{1}{6} | \frac{3}{6} |
| 4 | \frac{1}{6} | \frac{4}{6} |
| 5 | \frac{1}{6} | \frac{5}{6} |
| 6 | \frac{1}{6} | \frac{6}{6} |
| \, | Suma: | \sum\limits_{x=0}^3 x \, f_X(x) = \frac{21}{6} = 3.5 |
Ejercicio 6.22 Encuentre el valor esperado / la esperanza / el promedio del número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente.
Z := “El número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente”.
Valores que toma la variable: z = 0, 1, 2, 3.
\begin{aligned} E[Z] &= \sum_{t \in \mathbb{R}} t \, f_Z(t) = \sum_{t \in \mathbb{R}} t \, P[Z=t] \\ &= \sum_{z=0}^3 z \, f_Z(z) = \sum_{z=0}^3 z \, P[Z=z] \\ &= (0) \, P[Z=0] + (1) \, P[Z=1] + (2) \, P[Z=2] + (3) \, P[Z=3] \\ &= (0) \, \frac{1}{8} + (1) \, \frac{3}{8} + (2) \, \frac{3}{8} + (3) \, \frac{1}{8} \\ &= \frac{3}{8} + \frac{6}{8} + \frac{3}{8} \\ &= \frac{12}{8} \\ &= 1.5 \end{aligned}
Ejercicio 6.23 Suponga que en un juego de azar inicialmente se debe apostar \$ 10 000 pesos, luego se lanza un dado común y corriente de seis caras y por cada punto que salga en la cara superior del dado, el apostador recibe \$ 2 500.
¿A la larga, cuál será la ganancia-perdida promedio de el(los) apostador(es) por cada vez que se apueste?
Si X := “Resultado al lanzar, una vez, un dado común y corriente”, entonces Y = \$ 2500 X - \$ 10000 sería la variable aleatoria asociada a la ganancia-perdida de el(los) apostador(es).
| x | f_X(x) | y | f_Y(y) | y \, f_Y(y) |
|---|---|---|---|---|
| 1 | \frac{1}{6} | -7500 | \frac{1}{6} | \frac{-7500}{6} |
| 2 | \frac{1}{6} | -5000 | \frac{1}{6} | \frac{-5000}{6} |
| 3 | \frac{1}{6} | -2500 | \frac{1}{6} | \frac{-2500}{6} |
| 4 | \frac{1}{6} | 0 | \frac{1}{6} | \frac{0}{6} |
| 5 | \frac{1}{6} | 2500 | \frac{1}{6} | \frac{2500}{6} |
| 6 | \frac{1}{6} | 5000 | \frac{1}{6} | \frac{5000}{6} |
| \, | \, | \, | Suma: | \sum\limits_{i=1}^{6} y_i \, f_Y(y_i) = \frac{-7500}{6} = -1250 |
Si hubiese tenido en cuenta las propiedades del valor esperado: \begin{aligned} E[Y] &= E[2500 X - 10000] \\ &= 2500 E[X] - 10000 \\ &= 2500 (3.5) - 10000 \\ &= -1250 \end{aligned} Es decir que, a la larga y en promedio, el(los) apostador(es) perderán \$ 1 250 pesos por cada vez que se apueste.
Ejercicio 6.24
En el ejercicio 3.13 de la página 92 se presenta la siguiente distribución de probabilidad de X, el número de imperfecciones que hay en cada 10 metros de una tela sintética, en rollos continuos de ancho uniforme
x 0 1 2 3 4 f(x) 0.41 0.37 0.16 0.05 0.01 Calcule el número promedio de imperfecciones que hay en cada 10 metros de esta tela.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.1 (3.13)
Ejercicio 6.25
La función de densidad de la variable aleatoria continua X, el número total de horas que una familia utiliza una aspiradora durante un año, en unidades de 100 horas, se da en el ejercicio 3.7 de la página 92 como f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Calcule el número promedio de horas por año que las familias utilizan sus aspiradoras.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.13 (3.7)
6.4.1 Valor esperado de una función
El valor esperado de una función g(X) de una variable aleatoria discreta X es: \begin{aligned} \mu_{g(X)} &= E[g(X)] \\ &= \sum_{t \in \mathbb{R}} g(t) \, f_X(t) \\ &= \sum_{t \in \mathbb{R}} g(t) \, P[X=t] \end{aligned}
El valor esperado de una función g(X) de una variable aleatoria continua X es: \begin{aligned} \mu_{g(X)} &= E[g(X)] \\ &= \int_{t \in \mathbb{R}} g(t) \, f_X(t) \, dt \\ &= \int_{-\infty}^{\infty} g(t) \, f_X(t) \, dt \end{aligned}
Ejercicio 6.26 Encuentre la ganancia-perdida promedio de un apostador, si de entrada tiene que apostar \$ 500, y si gana \$ 100 por el número al cuadrado de caras que aparecen en el lanzamiento de una moneda normal tres veces.
Sea Z := “El número de caras que aparecen en el lanzamiento de una moneda normal tres veces”. La función de ganancia-perdida sería g(Z) = 100 \, Z^2 - 500.
\begin{aligned} E[100 \, Z^2 - 500] &= \sum_{t \in \mathbb{R}} \left(100 \, t^2 - 500\right) \, P[Z=t] \\ &= \sum_{z=0}^3 \left(100 \, z^2 - 500\right) \, P[Z=z] \\ &= (-500) \, \frac{1}{8} + (-400) \, \frac{3}{8} + (-100) \, \frac{3}{8} + (400) \, \frac{1}{8} \\ &= (-500) \, \frac{1}{8} + (-1200) \, \frac{1}{8} + (-300) \, \frac{1}{8} + (400) \, \frac{1}{8} \\ &= (-1600)\, \frac{1}{8} \\ &= -200 \end{aligned}
Ejercicio 6.27 Si inicialmente se debe apostar \$ 7500 pesos, y se gana el resultado de un dado común elevado al cubo y multiplicado por \$ 100.
¿A la larga, cuál será la ganancia-perdida promedio de un apostador por cada vez que apueste?
Sea X := “Resultado al lanzar, una vez, un dado común y corriente”. Y = g(X) = 100 X^3 - 7500 sería la variable aleatoria asociada a la ganancia-perdida.
Además, \begin{aligned} E[Y] &= E\left[100 X^3 - 7500\right] \\ &= 100 E\left[X^3\right] - 7500. \end{aligned}
| x | f_X(x) | g(x)=x^3 | g(x) \, f_X(x) |
|---|---|---|---|
| 1 | \frac{1}{6} | 1 | \frac{1}{6} |
| 2 | \frac{1}{6} | 8 | \frac{8}{6} |
| 3 | \frac{1}{6} | 27 | \frac{27}{6} |
| 4 | \frac{1}{6} | 64 | \frac{64}{6} |
| 5 | \frac{1}{6} | 125 | \frac{125}{6} |
| 6 | \frac{1}{6} | 216 | \frac{216}{6} |
| \, | \, | Suma: | \sum\limits_{x=1}^6 g(x) \, f_X(x) = \frac{441}{6} = 73.5 |
\begin{aligned} E[Y] &= 100 E\left[X^3\right] - 7500 \\ &= 100 (73.5) - 7500 \\ &= -150 \end{aligned}
Es decir que por cada vez que se apueste, a la larga en promedio se perderán \$ 150.
Ejercicio 6.28
¿Cuál es la utilidad promedio por automóvil que obtiene un distribuidor, si la utilidad en cada uno está dada por g(X) = X^2, donde X es una variable aleatoria que tiene la función de densidad del ejercicio 4.12?
Ejercicio 4.12: Si la utilidad para un distribuidor de un automóvil nuevo, en unidades de $5000, se puede ver como una variable aleatoria X que tiene la siguiente función de densidad f(x) = \begin{cases} 2(1 - x) & 0 < x < 1 \\ 0 & \text{en otro caso} \end{cases} Calcule la utilidad promedio por automóvil.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.21 (4.12)
Ejercicio 6.29
El tiempo total que una adolescente utiliza su secadora de pelo durante un año, medido en unidades de 100 horas, es una variable aleatoria continua X que tiene la siguiente función de densidad f(x) = \begin{cases} x & 0 < x < 1 \\ 2 - x & 1 \leq x < 2 \\ 0 & \text{en otro caso} \end{cases} Utilice las propiedades de valor esperado para evaluar la media de la variable aleatoria Y = 60X^2 + 39X, donde Y es igual al número de kilowatts-hora que gasta al año.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.58
6.5 Varianza
Así como se puede calcular el promedio para una variable aleatoria, también se puede obtener su varianza, y por ende su desviación estándar.
Estas medidas dan cuenta de la variabilidad, con respecto a la media, de los valores que puede tomar la variable aleatoria (teniendo en cuenta adecuadamente las diferentes probabilidades / ponderaciones de los valores que toma la v.a.).
La varianza de una variable aleatoria X es: \begin{aligned} \sigma_X^2 &= Var[X] \\ &= E \Big[ \big( X - \mu_X \big)^2 \Big] \\ &= E\big[X^2\big] - \mu_X^2 \end{aligned} donde \mu_X = E[X] es el valor esperado / media de la variable aleatoria X.
Retomando este ejercicio:
Suponga que un distribuidor de joyería antigua está interesado en comprar un collar de oro para el que tiene 0.22 de probabilidades de venderlo con $250 de utilidad; 0.36 de venderlo con $150 de utilidad; 0.28 de venderlo al costo y 0.14 de venderlo con una pérdida de $150. ¿Cuál es su utilidad esperada?
Tomado de: Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Ejercicio 4.8.
¿Cuál es la desviación estándar de la utilidad (daría una idea del “riesgo” o la “volatilidad”)?
Propiedades de la varianza:
- Var[X] \geq 0, para toda variable aleatoria X.
- Si X=a constante, entonces Var[X] = Var[a] = 0.
- Var[X + b] = Var[X].
- Var[a \, X] = a^2 \, Var[X].
Ejercicio 6.30 Encuentre la varianza del número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente.
Z := “El número de caras que aparecen al lanzar tres veces consecutivas una moneda común y corriente”.
Valores que toma la variable: z = 0, 1, 2, 3.
\begin{aligned} Var[Z] &= E\left[Z^2\right] - \left(E[Z]\right)^2 \\ &= \left(\sum_{z=0}^3 z^2 \, P[Z=z]\right) - (1.5)^2 \\ &= (0) \, \frac{1}{8} + (1) \, \frac{3}{8} + (4) \, \frac{3}{8} + (9) \, \frac{1}{8} - (1.5)^2 \\ &= \frac{3}{8} + \frac{12}{8} + \frac{9}{8} - (1.5)^2 \\ &= \frac{24}{8} - (1.5)^2 \\ &= 3 - (1.5)^2 \\ &= 0.75 \end{aligned}
Ejercicio 6.31 Encuentre la varianza y la desviación estándar del número de puntos que aparecen en la cara superior de un dado común y corriente de seis caras que se lanza una vez.
X := “Resultado al lanzar, una vez, un dado común y corriente”.
Valores que toma la variable: x = 1, 2, 3, 4, 5, 6.
| x | f_X(x) | x^2 \, f_X(x) |
|---|---|---|
| 1 | \frac{1}{6} | \frac{1}{6} |
| 2 | \frac{1}{6} | \frac{4}{6} |
| 3 | \frac{1}{6} | \frac{9}{6} |
| 4 | \frac{1}{6} | \frac{16}{6} |
| 5 | \frac{1}{6} | \frac{25}{6} |
| 6 | \frac{1}{6} | \frac{36}{6} |
| \, | Suma: | \sum\limits_{x=1}^{6} x^2 \, f_X(x) = \frac{91}{6} = 15.1666\bar{6} |
Var[X] = 15.1666\bar{6} - (3.5)^2 = 2.9166\bar{6}
SD[X] = \sqrt{2.9166\bar{6}} = 1.707825
Ejercicio 6.32
Considere la situación del ejercicio 4.32 de la página 119. La distribución del número de imperfecciones por cada 10 metros de tela sintética está dada por
x 0 1 2 3 4 f(x) 0.41 0.37 0.16 0.05 0.01 Calcule la varianza y la desviación estándar del número de imperfecciones.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.49 (4.32)
6.6 Desigualdad de Chebyshev
Descubramos un uso de media y desviación estándar.
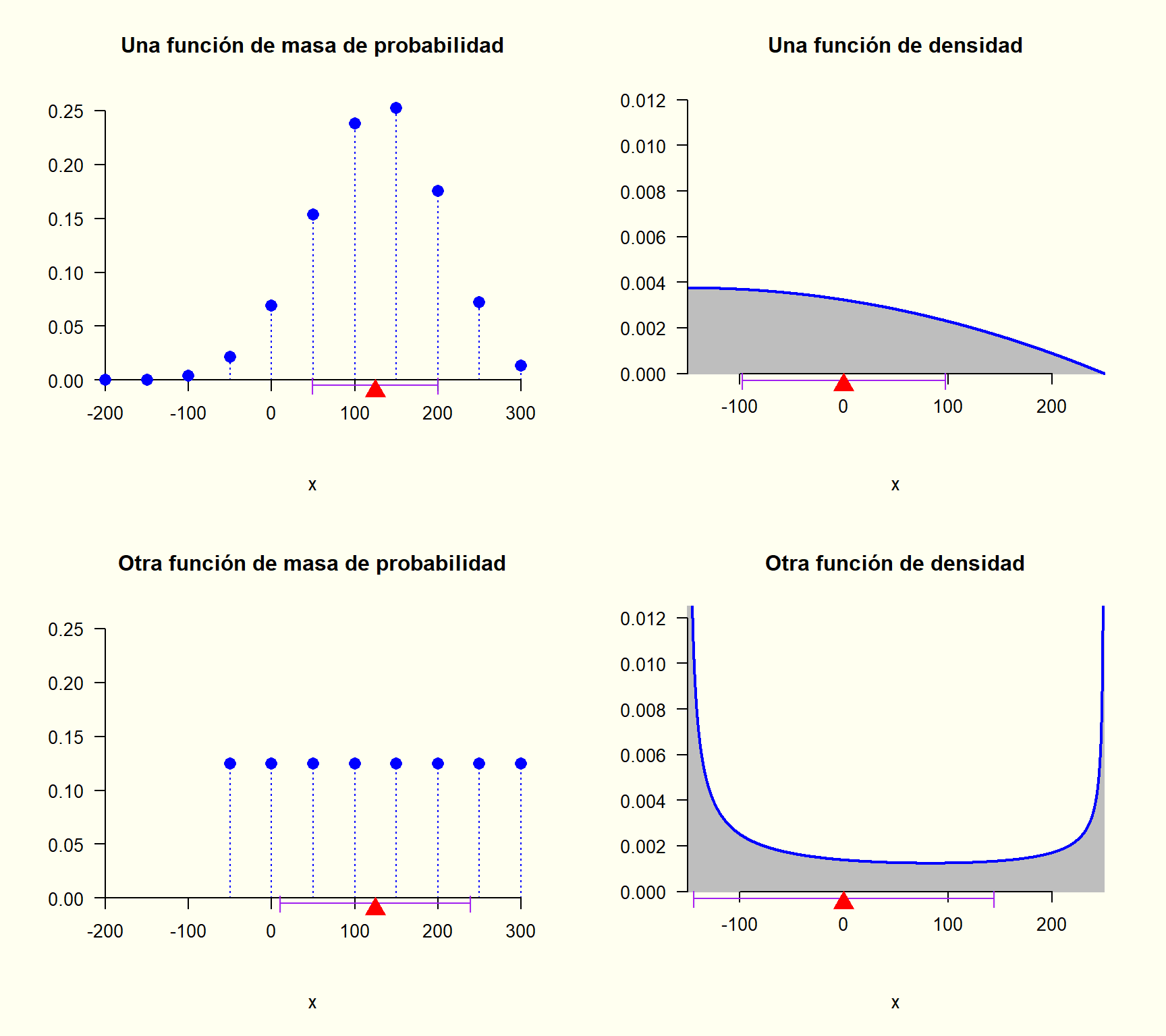
Para toda variable aleatoria X (denotando \mu_X = E[X] y \sigma^2_X = Var[X]), la probabilidad de que ésta tome valores a k desviaciones estándar de la media es por lo menos (es como mínimo) 1 - \frac{1}{k^2}. Es decir, \begin{aligned} P\big[\mu_X - (k) \, \sigma_X < X < \mu_X + (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ P\big[- (k) \, \sigma_X < X - \mu_X < (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ P\big[ |X - \mu_X| < (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \end{aligned} para k dado.
Por ejemplo, para k = 1 se concluye que, \begin{aligned} P\big[ |X - \mu_X| < (1) \, \sigma_X\big] &\geq 1 - \frac{1}{(1)^2} \\ P\big[ |X - \mu_X| < \sigma_X\big] &\geq 0 \\ P\big[\mu_X - \sigma_X < X < \mu_X + \sigma_X\big] &\geq 0 \end{aligned} para toda variable aleatoria X. Conclusión que es obvia, ya que toda probabilidad es mayor que cero. Sin embargo, para k > 1 tendríamos conclusiones más interesantes. Por ejemplo, para k = 2.5 se concluye que, \begin{aligned} P\big[ |X - \mu_X| < (2.5) \, \sigma_X\big] &\geq 1 - \frac{1}{(2.5)^2} \\ P\big[\mu_X - (2.5) \, \sigma_X < X < \mu_X + (2.5) \, \sigma_X\big] &\geq 0.84 \end{aligned} para toda variable aleatoria X (sin importar su distribución).
Por otro lado, si en \begin{aligned} P\big[\mu_X - (k) \, \sigma_X < X < \mu_X + (k) \, \sigma_X\big] &\geq 1 - \frac{1}{k^2} \\ \end{aligned} decimos que \epsilon = (k) \, \sigma entonces la desigualdad quedaría de la siguiente manera, P[\mu_X - \epsilon < X < \mu_X + \epsilon] \geq 1 - \frac{\sigma_X^2}{\epsilon^2} para \epsilon > 0 y cualquier variable aleatoria X (denotando \mu_X = E[X] y \sigma^2_X = Var[X]).
¿De qué me sirven los anteriores resultados? ¿para qué los puedo utilizar?
Ejemplo 6.1 Supongamos que una fabrica produce en promedio 1500 unidades al día, con una desviación estándar de aproximadamente 300 unidades.
Entonces, sin importar la distribución (el mecanismo aleatorio detrás) de la variable aleatoria X: “número de unidades producidas por la fabrica al día”, podemos concluir que,
\begin{aligned} P[\mu_X - (k) \, \sigma_X < X < \mu_X + k \, \sigma_X] &\geq 1 - \frac{1}{k^2} \\ P[1500 - (k) (300) < X < 1500 + (k) (300)] &\geq 1 - \frac{1}{k^2} \end{aligned}
De allí (sin conocer nada más acerca de la variable aleatoria X) puedo asegurar que como mínimo el 84% de los días se producen entre 750 y 2250 unidades al día (llego a esta conclusión tomando k = 2.5).
Ejercicio 6.33 ¿A partir de la información el ejemplo anterior, como mínimo, qué PROPORCIÓN de los días se producirán entre 1000 y 2000 unidades?
Tome \epsilon = 500.
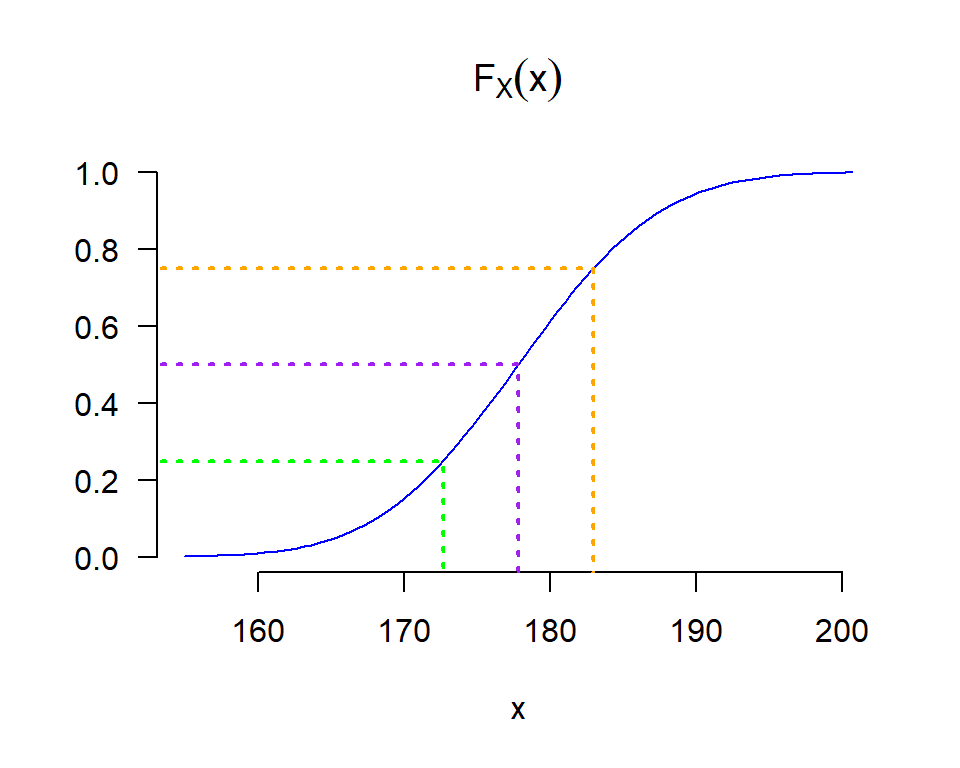
Ejemplo 6.2 Supongamos que la estatura media de los hombres adultos en cierto país es de aproximadamente 177.8 cm, con una desviación estándar de alrededor de 7.62 cm.
Entonces, sin importar la distribución (el mecanismo aleatorio detrás) de la variable aleatoria X: “estatura media de los hombres adultos”, se tiene que,
\begin{aligned} P[\mu_X - k \, \sigma_X < X < \mu_X + k \, \sigma_X] &\geq 1 - \frac{1}{k^2} \\ P[177.8 - 2 (7.62) < X < 177.8 + 2 (7.62)] &\geq 1 - \frac{1}{2^2} \\ P[162.56 < X < 193.04] &\geq 0.75 \end{aligned}
Es decir, al menos (como mínimo) el 75\% de los hombres adultos de ese cierto país tienen una estatura entre 162.56 y 193.04 cm.
Ejercicio 6.34 ¿A partir de la información el ejemplo anterior, entre qué estaturas estaría al menos (como mínimo) el 90\% de las estaturas de los hombres adultos de ese país?
Ejercicio 6.35
Una empresa eléctrica fabrica una bombilla de luz de 100 watts que, de acuerdo con las especificaciones escritas en la caja, tiene una vida media de 900 horas con una desviación estándar de 50 horas. A lo sumo, ¿qué porcentaje de las bombillas no duran al menos 700 horas? Suponga que la distribución es simétrica alrededor de la media.
Walpole, Myers & Myers (2012). Probabilidad y estadística para ingeniería y ciencias. (9a. ed.) Pearson Educación. Capítulo 4, Ejercicio 4.75
6.7 Cuantiles
El cuantil x_p, para p \in [0,1], de una variable aleatoria X es un valor que toma la variable tal que: P[X \leq x_p] \geq p \qquad \text{ y } \qquad P[X \geq x_p] \geq 1-p
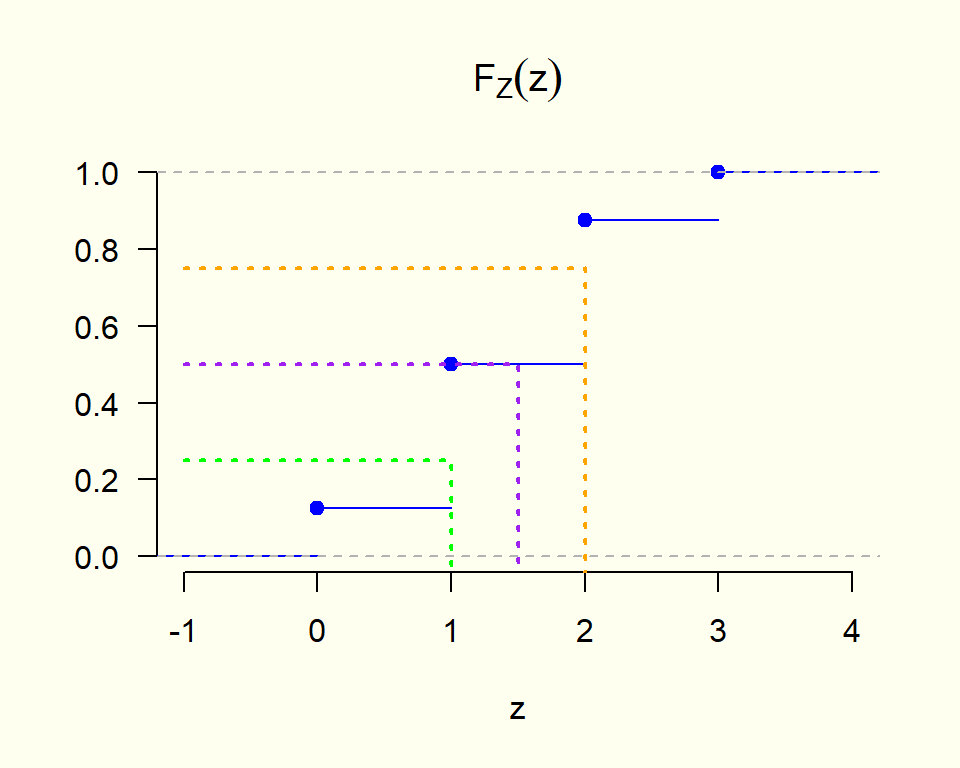
Ejercicio 6.36 Encuentre los cuartiles 1, 2, y 3 (cuantiles 0.25, 0.5 y 0.75) del número de caras que aparecen en el lanzamiento tres veces consecutivas de una moneda común y corriente.
Z := “El número de caras que aparecen en el lanzamiento tres veces consecutivas de una moneda común y corriente”.
Valores que toma la variable: z = 0, 1, 2, 3.
| z | P[Z = z] | P[Z \leq z] |
|---|---|---|
| 0 | \frac{1}{8} | \frac{1}{8} = 0.1250 |
| 1 | \frac{3}{8} | \frac{4}{8} = 0.5000 |
| 2 | \frac{3}{8} | \frac{7}{8} = 0.8750 |
| 3 | \frac{1}{8} | \frac{8}{8} = 1.0000 |
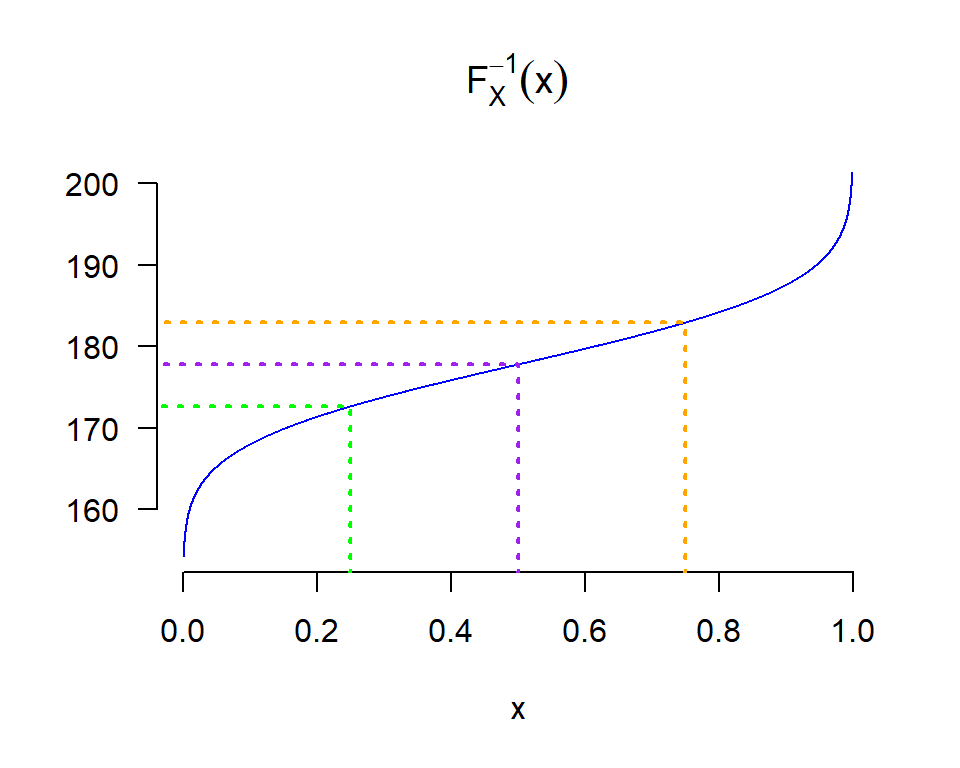
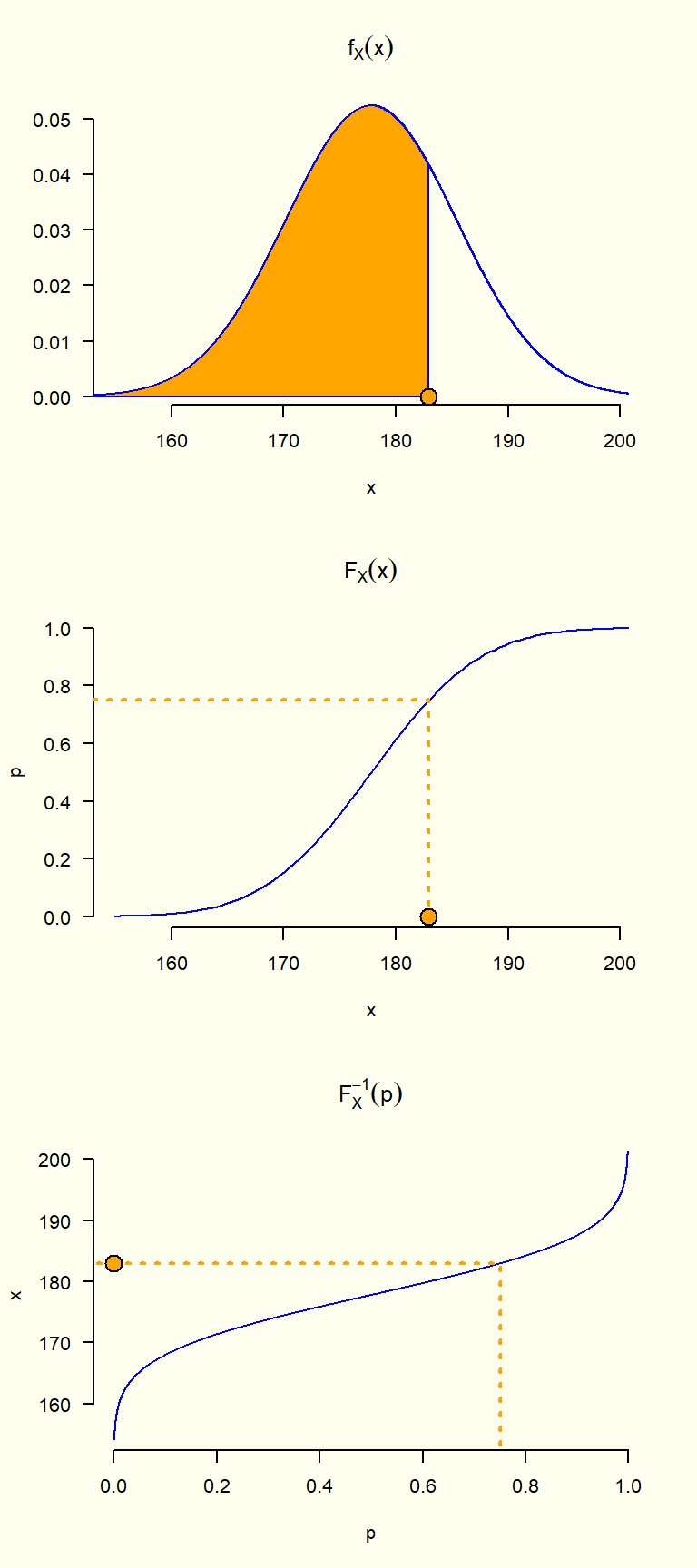
Note que para una variable aleatoria continua X, se tiene que, \begin{aligned} P[X \leq x_p] &= p \\ F_X[x_p] &= p \\ x_p &= F_X^{-1}(p) \end{aligned}
No olvides seleccionar y resolver ejercicios de un libro acerca de lo visto en esta sección (preferiblemente que tengan respuesta). Por ejemplo, selecciona ejercicios de las secciones 3.1 a 3.3, 4.1, 4.2 (sin incluir ejercicios de covarianza de variables aleatorias) y 4.4 del libro de Walpole o de las secciones 5.1 a 5.3 (v.a. discretas) del libro de Anderson (este libro no tiene secciones para variables aleatorias continuas en general).
De manera opcional, quien quiera puede buscar, consultar y leer acerca de: la moda, el coeficiente de variación, el coeficiente de asimetría, el coeficiente de apuntamiento, los momentos, la función generadora de momentos y la función característica de una variable aleatoria.