Apéndice A — Repaso: Conjuntos

En este apéndice se hace un repaso de algunos aspectos básicos relacionados con el manejo de conjuntos.

A.1 Notación

Definición de un conjunto por comprensión: A = \{a : a \in \mathbb{N} \text{ y } 1 \leq a \leq 6 \}
Definición de un conjunto por extensión: A = \{1,2,3,4,5,6\}
Conjunto vacío: Conjunto que no tiene ningún elemento. (\emptyset)

Igualdad: Dos conjuntos A y B que tengan los mismos elementos son el mismo conjunto. (A = B).
Contenencia: Un conjunto A es un subconjunto del conjunto B si cada elemento de A es a su vez un elemento de B. (A \subset B)

Unión: Es el conjunto de todos los elementos que pertenecen al conjunto A o al conjunto B. (A \cup B)
Intersección: Es el conjunto de todos los elementos que pertenecen al conjunto A y al conjunto B. (A \cap B)
Complemento: Es el conjunto de todos los elementos que pertenecen al conjunto universal y que no pertenecen a A. (A^C)
Diferencia: Es el conjunto de todos los elementos que pertenecen a A y que no pertenecen a B. (A \backslash B = A \cap B^C)
Diferencia simétrica: Es el conjunto de todos los elementos que pertenecen a A o que pertenecen a B, pero que no pertenecen a ambos a la vez. (A \triangle B = (A \cup B) \backslash (A \cap B))

Conmutativa: A \cup B = B \cup A y A \cap B = B \cap A.
Asociativa: A \cup (B \cup C) = (A \cup B) \cup C y A \cap (B \cap C) = (A \cap B) \cap C.
Distributiva: A \cup (B \cap C) = (A \cup B) \cap (A \cup C) y A \cap (B \cup C) = (A \cap B) \cup (A \cap C).
Leyes de Morgan: (A \cup B)^C = A^C \cap B^C y (A \cap B)^C = A^C \cup B^C.
Con el conjunto vacío: \emptyset^C = \Omega, A \cup \emptyset = A y A \cap \emptyset = \emptyset.
Con el conjunto universal: \Omega^C = \emptyset, A \cup \Omega = \Omega y A \cap \Omega = A.
Con el complemento: A \cup A^C = \Omega, A \cap A^C = \emptyset y (A^C)^C = A.

Ejemplo A.1 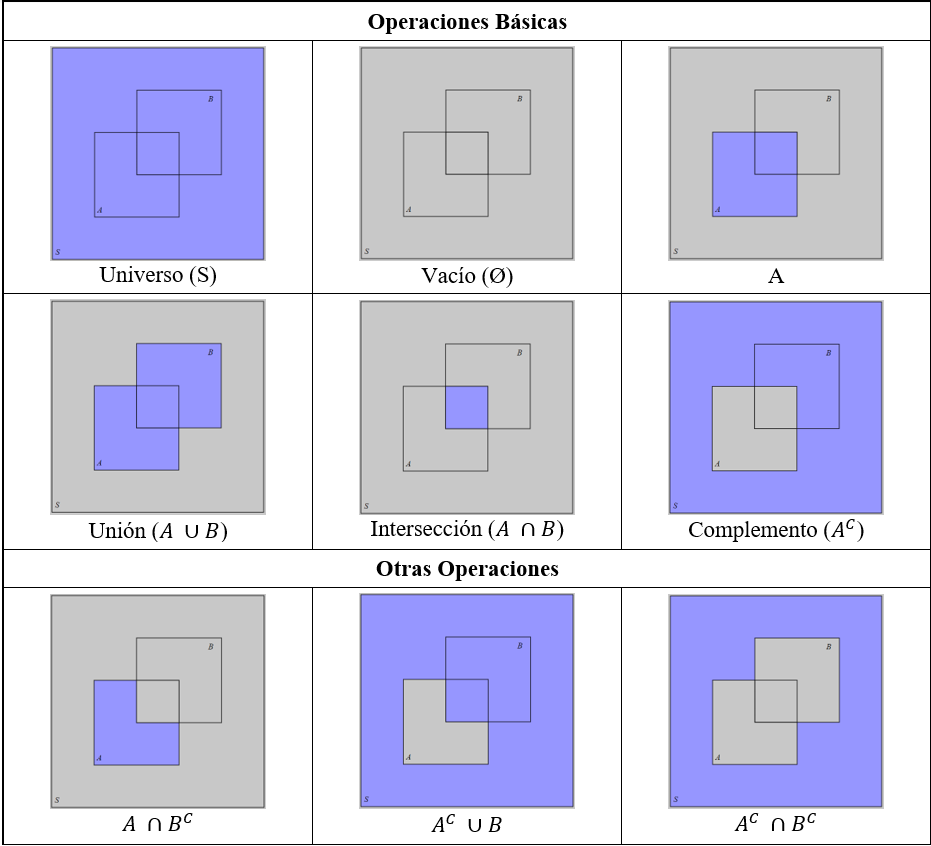Ir a Venn Diagram App